Оптимизация на простых типах данных. Часть №2 «Числа»
Мы подготовили расшифровку вебинара в двух частях. Первая часть — про строки и работу с ними, вторая — про числа.
Статья будет полезна разработчикам на Python и C/C++, которые хотят научиться трюкам для ускорения кода, а также программистам на других языках, которым интересны фишки, связанные с типами данных.

Числа
Что же происходит с числами? Числа как тип данных тоже кодируются битами ноликов и единичек. Вот пример.

Итак, мы умеем хранить положительные числа. А если нам надо каким-то образом зафиксировать ещё и знак числа? Числа же могут быть как положительными, так и отрицательными.
Из-за того, что нам удобно выделять память не отдельными битами, а байтовыми блоками, оказывается, что мы не можем добавить к нашему числу дополнительный 9-й бит и использовать его для хранения знака числа.
Так что нам надо отрезать 1 бит от 8-битного числа (на нашем маленьком примере).

Посмотрим на левую часть. У нас есть положительные числа. В этом случае на самой левой позиции всегда будет записан нолик, а дальше — то число, которое мы хотим увидеть.
А теперь смотрите на нижнюю часть слайда — там есть отрицательные числа. Что делать? Просто записать единичку и следом записать такое же число, как и в случае с положительным — рабочий вариант. Это называется прямой код: мы сравниваем в первой строке, как выглядит чёрная часть массивчика, сравниваем во второй строке и видим, что они равны. Удобно.
Но оказывается, что если мы хотим сложить 75 и –75, то в прямом коде это делать неудобно, потому что у нас не получится 0. Попробуйте сами.
Дополнительный и обратный коды
Поэтому эволюционно в computer science было решено, что удобнее использовать обратный код. Это когда мы берём и все символы (если на первом месте единичка) переворачиваем. В целом вариант удобный, и тут уже при сложении 75 и –75 получается –0. Вроде бы уже сильно ближе, но что это вообще за –0 такой?
Вместо этого есть возможность использовать дополнительный код. Обратный код от дополнительного отличается тем, что вместо простой инверсии мы в конце добавляем ещё единичку. То есть у нас в самой правой ячейке был нолик, а теперь там единичка.
При этом если бы у нас уже была единичка в самой правой ячейке, то в дополнительном коде у нас стал бы нолик, а единичка перенеслась бы в следующий разряд.
В таком случае сложение двух чисел в дополнительном коде будет давать нам просто +0. Что мы имеем благодаря такому хранению целых чисел — мы можем сохранить в 8 битах (в 1 байте) числа от 27–1 до 27. В отрицательных числах просто на одно значение больше.
Зачем всё это знать
Давайте посмотрим пример, на который я сама натыкалась в Java несколько раз, скопипастила его с одного сайта.
public class OverflowUnderflow {
public static void main(String args[]){
//roll over effect to lower limit in overflow
int overflowExample = 2147483647;
System.out.println("Overflow: "+ (overflowExample + 1));
//roll over effect to upper limit in underflow
int underflowExample = -2147483648;
System.out.println("Underflow: "+ (underflowExample - 1));
}
}
26
Overflow: -2147483648
Underflow: 2147483647В чём суть. Java, несмотря на то, какой это большой и полезный язык с количеством разных функций, имеет такую особенность: если взять максимальное целое число, которое влезает в 4 байта, в положительном у нас получится
overflowExample, а в отрицательном underflowExample. В коде видно, что underflowExample на единичку по модулю больше, то есть у нас в отрицательном поле есть на 1 резервное число больше.ОК, добавим к максимальному числу единичку, из минимального числа вычтем единичку и выведем это на экран. И оказывается, что у нас уменьшенное минимальное число больше, чем увеличенное максимальное.
И вот такое перескакивание через границу может вам встретиться в реальном коде. Я сама такое встречала, когда мне важно было посчитать количество фотографий у пользователя. Это был фотограф, который фотографировал всё, до чего дотягивался, и было довольно неприятно, когда ты пытаешься посчитать количество фотографий, а у тебя на выходе внезапно отрицательное число. На это всегда надо обращать внимание. Зная, как оно устроено внутри, вы будете понимать предпосылки и корни возможных проблем.
Длинная арифметика
Далеко не всегда числа у нас такие, как в примерах. Давайте попробуем посчитать зарплату какого-то бизнесмена. Чтобы не так грустно было считать, представим, что это за год.

В зависимости от языков программирования у нас есть разные варианты. Тот же Python умеет считать длинную арифметику из коробки. В Java, насколько я помню, она тоже есть в дополнительной библиотеке. А вот во времена моего детства нас такие штуки заставляли писать руками, чтобы понимать, что происходит в библиотеках, когда мы переключаемся на вычисления длинных чисел.
Итак, варианты.
Давайте хранить наши десятичные числа в массиве, под каждую цифру — своя ячейка. Поэтому, когда захотим складывать, мы будем делать это по цифре. Временами у нас будут ситуации, когда нам будет необходим перенос через разряд. Для этого заведём ещё одну дополнительную переменную и будем её периодически прибавлять, вовремя обнулять — ничего сложного, но надо это реализовать аккуратно.
Какие у такого сложения могут быть подводные камни? Будет оно работать быстро или медленно? Когда именно оно будет работать медленно?
У нас линейная сложность, много девяток, мы можем выделить под результат массив неправильного размера, и он у нас не влезет. Чем больше у нас цифр, тем дольше работает наша программа. Причём чем больше цифр в самом длинном из чисел.
ОК, с суммированием всё неплохо, с вычитанием тоже.
А что, если в длинной арифметике нам нужно сделать перемножение? В школе всё было просто: в столбик, сдвигаем цифры, всё здорово. А в случае с длинной арифметикой с ходу непонятно, что делать.
Есть простой вариант: мы можем в цикле прибавлять меньшее из чисел, например 321, и в цикле 321 раз складываем 876 435.

В принципе, работать будет. Сложность тут равна длине первого числа, перемноженной на значение второго числа. Может, и многовато, особенно потому, что значение существенно больше, чем длина числа.
Но есть вариант удобнее, если понимать, что происходит внутри.
Давайте посмотрим на простые (не такие длинные) числа и запишем их двоичной системе счисления.
Вот у нас семёрка. Она будет выглядеть как три единички подряд в двоичной системе.

А вот 14, тоже несложно — 21+22+23. Или расписать иначе, как 2*(20+21+22), а это мы уже видели у семёрки.
Тут полезно заметить, что оба этих числа выглядят друг на друга подозрительно похожими с точностью до нолика справа. Это как раз связано с тем, что одно является другим, умноженным на 2. Поэтому степень двойки в сумме повышается. И выходит, что мы, зная битовую форму числа, быстро можем умножать на 2.
Для небольшой проверки рассчитайте в двоичной форме число 28.
Как это поможет в исходной задаче?
Мы же хотели умножать одно длинное число на другое длинное, помните? Давайте представим число 321 в двоичном виде, а точнее, тут нам удобнее его представить в форме сумм степеней двойки.

Соответственно, каждую из этих трёх строчек мы можем получить в двоичной форме довольно быстро, просто просчитав одно исходное число 876 435. У нас есть специальный побитовый оператор, который позволяет подобное.

Вот так это число выглядит в двоичной форме.
У первого числа справа 8 ноликов, у второго справа 6 ноликов, у последнего справа нулей нет.
Вопрос: если мы говорим, что длинная арифметика — это долго, что у нас десятичные числа долго складываются, что это линейное время, почему число, записанное в двоичной форме (которая всегда длиннее десятичной), работает быстро?
Тут бы хорошо рассказать, как оно вообще бывает, но сократим: процессор устроен так, что в нём есть специальный кусочек под названием сумматор. Этот двоичный сумматор как раз и предназначен для очень быстрого суммирования двоичных чисел. Восхитительная штука. Перекодировка тоже происходит почти моментально.
Результат такого вычисления позволяет нам сначала узнать, чему будет равно 26. Какие тут варианты — исходное число не помещается, но мы можем сложить нужное количество раз число с самим собой. Сложив один раз, мы получим 2 в первой степени, сложив два раза — 2 во второй и так далее.
Итого мы сначала рассчитаем 26 и прибавим к нему 28. На вычисление 26 у нас потребуется шесть операций сложения, каждая за линейное время, на 28 мы просто сделаем ещё два сложения числа с самим собой. И получится результат.
Для процессора все числа двоичные, но когда мы используем длинную арифметику, как мы сделали в примере на массивах, у нас в одной ячейке хранится не одна цифра и не один бит информации, а в лучшем случае однобайтное число. А как вы помните, один даже беззнаковый байт — это 27.
И вместо того, чтобы просто складывать два числа, на самом деле под капотом происходит сложение одних 8 битов с другими 8 битами. Вот и получается ещё дольше, чем в нашем примере.
Что ещё важно. Понимание алгоритмов — это здорово, но существует следующий уровень — понимание не только алгоритмов, но и устройства процессоров, потому что там внезапно много интересного. Оттуда же можно почерпнуть, что хоть двоичная система кажется базисом, но математически она не самая оптимальная, и во всём этом реально интересно разбираться.
Вот что ещё можно делать для того, чтобы избегать самостоятельной реализации длинной арифметики и не мучиться со сложными умножениями (заметьте, мы ещё не обсуждали с вами деление и возведение в степень).
Зачастую для решения задачи нам достаточно не получить точный ответ, а узнать какой-то признак. Например, у нас есть задачка.
Собрали урожай яблок на 23 килограмма, собирали урожай вдевятером. Делить надо всё поровну. Оставшиеся яблоки отвезут бабушке.Сколько яблок надо отвезти бабушке?
Пока у нас 23 кг, всё не так уже плохо: бабушка получает остаток от деления 23 на 9, то есть 5 кг.
А если количество кг яблок не влезает в целочисленную переменную?
То есть у нас есть десятки тысяч рабочих на комбайнах. Чтобы просуммировать такое значение и поделить его на количество рабочих, нам не обязательно собирать все яблоки в единую кучу. Мы можем просто результат каждого рабочего взять по модулю и суммировать дальше их, всякий раз оставляя только этот самый признак.
Условно вот что мы вычисляем в этот момент времени: если бы работы выполнял только один рабочий и мы бы все его яблоки распределили по остальным рабочим поровну и взяли бы остаток, мы бы получили вклад этого рабочего в остаток яблок для бабушки.
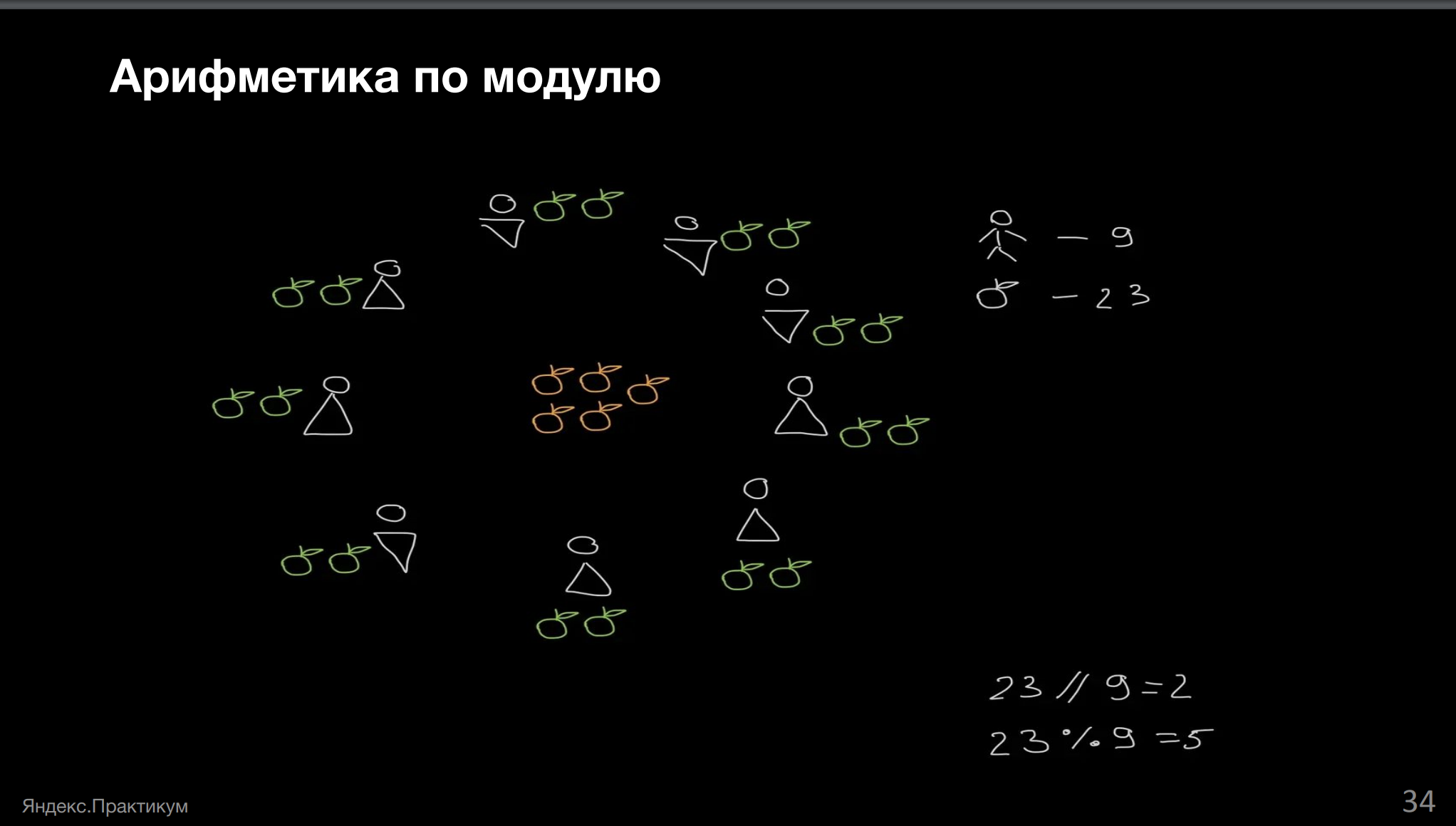
Но затем оказывается, что работал ещё и второй рабочий, вот он докидывает в кучу свои яблоки, из докинутых яблок мы понимаем, что можно опять поровну всем раздать, поэтому обновляется процент.
То есть не надо вычислять какую-то гигантскую сумму, а можно просто всякий раз брать остаток от деления по модулю. Во многих языках программирования это обозначается как процент, но не имеет отношения к привычным процентам, имейте в виду.
Удобно. Работает. Но не идеально и оставляет простор для ошибок.
Где всё это применять
Во многих местах, например, в кибербезопасности — тайна вашей переписки.
У нас есть какое-то сообщение, к которому мы добавляем ключ и считаем специальную чек-сумму (отсылка к хэшам, о которых мы говорили), и отправляем письмо.
Адресат получает письмо, получает чек-сумму и сверяет, что получил всё нужное, затем раскодирует всё своим ключом и читает сообщение. Вдруг в системе появляется злоумышленник, который берёт своё вредоносное письмо, подсовывает вместо нужного, свой ключ и свою чек-сумму.
Адресат получает всё это и расшифровывает на своей стороне. Понимает, что расшифровалась какая-то фигня, чек-сумма не совпадает, всё плохо.
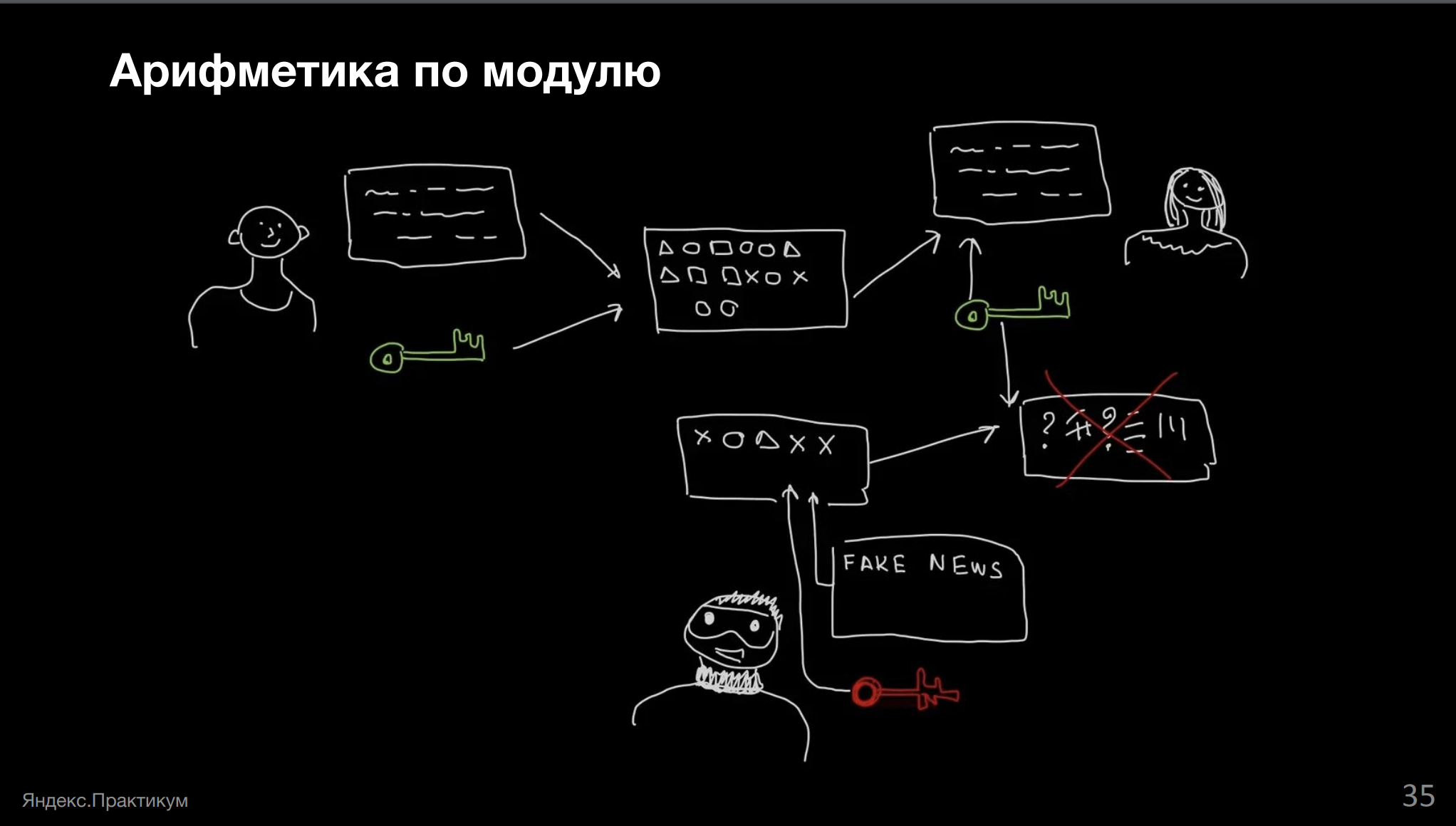
Нам важно брать хэш по модулю для того, чтобы не перейти за границу наших целочисленных вычислений. Помните пример с Java? Может оказаться, что наша чек-сумма разъедется потому, что вместо положительного числа у нас получится отрицательное.
Таких применений арифметики по модулю много, они встречаются регулярно, просто часто скрыты от глаз.
Как видите, на самом деле в алгоритмах куда больше интересного, чем может показаться со стороны. Сильно больше, чем можно вместить в один пост (да и в два). Если у вас есть какие-то вопросы или уточнения по тексту или видео вебинара — пишите в комментарии, буду рада ответить.
