Оптимизация на простых типах данных
Мы подготовили расшифровку вебинара в двух частях. Первая часть — про строки и работу с ними, вторая — про числа.
Статья будет полезна разработчикам на Python и C/C++, которые хотят научиться трюкам для ускорения кода, а также программистам на других языках, которым интересны фишки, связанные с типами данных.

В процессе написания кода я сажала огромное количество багов и правила примерно такое же количество, посаженное коллегами. Всё это активно прокачивало скиллы понимания разных частей программирования. Я писала на турбопаскале, С, С++, Python и Java, последние полгода я пишу на Go.
Начну с короткой истории из жизни. На собеседование по Go я пришла с фразой: «Привет, я иду к вам Go-разработчиком, но до сего дня не написала на Go ни строчки». Давайте разберёмся, почему таких людей вообще берут на работу.
Важно именно мышление.
Алгоритмическое мышление позволяет выстраивать свои программы в достаточно логичные цепочки, которые легко реализовать в виде кода на любом другом языке и достаточно легко поддерживать.
Человек, который умеет мыслить алгоритмически, чаще ценится компаниями. В чём преимущество: выстроив тип мышления, можно быстро менять стек технологий, на котором вы работаете, и при этом не чувствовать большой просадки по своему уровню. То есть начинаете джун-разработку на Django, качаетесь до мидла или сениора, потом происходит какое-то политическое событие, из-за которого Django перестаёт поддерживаться. Это маловероятная история, но вы понимаете сам посыл.
Или, например, вам предложили проект, который целиком соответствует вашим внутренним ценностям, но он целиком на Go. И непонятно, как переходить, и начинать ли опять с позиции джуна.
Программирование и начальная школа
Мы все учились считать, и у нас были камешки для счёта. Хотим сложить — берём нужное число камешков в одну руку, новое число камешков в другую руку и складываем их вместе, а потом пересчитываем, что получилось.
Когда камешков становится много, например 12 и 22, ситуация усложняется: их как минимум неудобно с собой носить. В процессе обучения в школе мы развиваем свой математический аппарат для того, чтобы научиться существенно быстрее выполнять те же самые действия и затрачивать меньше ресурсов.
С алгоритмическим программированием происходит то же самое. Совершенно нет проблем с тем, чтобы придумать многие алгоритмы программирования самостоятельно, например, поиск в ширину, один из самых известных алгоритмов на графах. Я преподавала у школьников — многие из них, встретив задачу с жёсткими ограничениями и невозможностью сдать плохое решение, в конце концов где-то за неделю–полторы выдают решение, аналогичное существующему алгоритму, но без подсматриваний в статьи и книги.
В общем, придумать — не проблема. Но если вы заранее знаете какие-то алгоритмы, вы сможете их применить намного быстрее, а сэкономленное время потратить на более интересные задачи или на то, чтобы отдохнуть. Вариантов много.
Причём математическая база для этого нужна средняя, обычно хватает школьных знаний, всё, что проходится по математике до 9-го класса. Вам не нужно быть победителем олимпиад по математике или лучшим в физмат-классе, чтобы освоить алгоритмы.
Кроме быстрого перехода на другой стек есть и вторая причина, по которой полезно знать алгоритмы: мы экономим время и ресурсы и позволяем компании на одних и тех мощностях делать больше и получать больше выгоды. Например, давать доступ к сервису большему числу пользователей и зарабатывать больше денег.
Итак, к делу. Давайте начнём со строк.
Строки

Кажется, что строки — это просто. Вот у нас в детстве были кубики, мы их складывали в буковки рядом и читали получившиеся из них слова. Потом слова складывались в предложения, предложения в абзацы и так далее.
В программировании это выглядит похожим образом. Для многих читать слова по буквам было ощутимо проще, чем разбираться со временем на часах или, скажем, с календарями. Хотя на деле в мире разработки оказывается, что строки тоже куда проще, чем работа с датой и временем. Но не потому, что строки элементарны, а потому, что работа с датой и временем совершенно не простая, там множество ответвлений и краевых проблем, с которыми чаще всего разработчик не сталкивается в работе, но что-то может пойти не так. И это надо учитывать.
Вот и со строками всё тоже непросто, есть много мест, где можно с размаху наступить на пару граблей сразу.
Как и в чтении у школьников, строки складывают символы в единую строку. Казалось бы, и там, и там у нас есть две половинки нашего кода.

В одном месте на Python, в другом на Go мы записали одну и ту же строку в переменную. Но в одном случае мы решили взять первый элемент и получили целый иероглиф, а во втором случае взяли элемент и получили какое-то странное число. И как с этим взаимодействовать, понятно далеко не всегда.
Давайте разберёмся, что же это за число.
Это число на самом деле — байт. В нашем случае иероглифы обычно требуют существенный объём памяти просто для того, чтобы их записать и иметь впоследствии возможность отобразить тот самый иероглиф, который мы хотим.
В обоих случаях строки — это последовательности, но в одном случае у нас строка — последовательность отдельных символов, в другом — последовательность байтов.
С другой стороны, в том же Go у нас есть возможность работать со строками как с последовательностью символов. Это то, что называется Unicode-safe-библиотекой. Она позволяет делить строку, состоящую из unicode-символов, на отдельные логические части вместо отдельных байтов. Но что же происходит под капотом? Казалось бы, хочется привести всё к единому знаменателю.
И то, и другое у нас на самом деле — массивы с какими-то элементами, просто в Python у нас более высокоуровнево всё выполнено и, соответственно, элемент, который мы записываем, это последовательность байтов. А в Go элемент, который мы записываем, — это отдельный единый байтик.
Таких различий достаточно много в разных языках. Это то, на что тоже следует обращать внимание.
230 в десятичной системе счисления — первый байт первого символа. Обычно иероглифы записываются 4 байтами, но это только первая часть этого иероглифа. У разных иероглифов первая часть может быть одинаковой.
Скорее всего, в ваших программах не будет каких-то особых проблем с тем, что вы работаете с иероглифами или с эмоджи, у которых странная длина символов — вы просто будете работать с кириллицей и латиницей, их везде легко обрабатывать.
Теперь более наглядно. Давайте разберёмся, что такое длина строки.

Кажется, что этой функцией мы пользуемся регулярно, например, печатаем что-то в каком-нибудь файлике, и он нам внизу сразу показывает изменение количества символов на странице. Здорово и удобно.
Но когда мы работаем со строкой в контексте программирования, хочется понимать, что такое длина строки. И тут возникает интересный вопрос: длина строки — это количество символов или количество байтов?
Но чаще всего говорят про количество символов.
В обычной жизни, когда у нас есть строка с буквами и мы хотим посчитать, сколько же там символов, всё просто. Берём в руки карандаш, тыкаем по монитору и считаем: 5, 10, 15… Перемещаем карандаш вперёд, высчитывая символы, потому что сразу в уме мы не можем увидеть, сколько же их. Тут их вроде как 127.

То, что я сейчас описала — это линейный алгоритм. То есть в процессе, чтобы посчитать длину нашей строки, мы прошли по каждому отдельному символу и потратили какое-то время, чтобы запомнить, что предыдущая длина строки увеличилась на единичку.
Ну ок, когда их 127, это не так уж долго, вы потратите на счёт полминуты. Проблема в том, что тексты бывают и очень большими. Допустим, статья в Википедии. Или «Война и мир». Если считать количество символов линейно и на подсчёт, скажем, 15 букв тратить 1 секунду, то «Война и мир» станет неплохим таймкиллером.
При этом в обычном мире строки — это массивчики. В каждой ячейке лежит своя буква, буквы складываются, и для того, чтобы посчитать длину, мы прибегаем к массиву. Как-то не очень получается, да?
Если бы не существовало способов оптимизации, мы бы тратили уйму времени. Поэтому хорошо, что разработчики языков молодцы, подумали о нас и поняли, что очень часто нужно считать длину строки. В том же ворде, представьте себе, если бы при наборе каждого нового символа или его стирании вместо того, чтобы узнать это небольшое изменение, вам бы пришлось пересчитывать заново всю длину всего файла. Жуть же. А вы курсовую пишете, например. Скорее всего, если бы ваш текстовый редактор работал синхронно, он бы ещё и зависал.
Поэтому для того, чтобы разработчикам было проще жить, решили вдобавок к каждой строке хранить в отдельном месте значение её длины. Соответственно, при добавлении пары символов длина увеличивается, при стирании — уменьшается.

Но мы платим за быстрое получение ответа определённым количеством памяти. И если у нас все строки длиннющие, это важно, потому что нам за одинаковое время будет и миллиард символов в строке высчитываться, и десять миллиардов, с такой же скоростью.
А если у нас в строке всего три символа и мы в основном работаем с короткими строками, получается, что вместо гигантской выгоды мы получили какое-то небольшое преимущество.
И вообще мы длину рассчитываем очень редко, зато уже отдали какое-то количество памяти под хранение этой длины. Это особенность современного программирования: языки достаточно высокоуровневые, в них уже о многом подумали и многое упростили. Но надо понимать, с какой точки мы стартовали — сначала было не очень радостно из-за того, что у нас массив, но потом стало получше.
Про оптимизацию
Как решить, стоит оптимизировать программу или нет?

Какие будут характеристики входных данных?
Представим, что ваша программа берёт на вход разные входные данные, например тексты переписок пользователей, то есть целиком дамп сообщений между близкими друзьями. Это существенный объём текстовой информации, скорее всего, будут ещё и картинки, это тяжело.
А вот если мы решаем почти такую же задачу, но вместо этого смотрим переписки деловых партнёров «заказчик-исполнитель», там будет совершенно другой объём входных данных.
Критично ли, чтобы эта функция работала быстро?
Здесь тоже понятно — иногда нас вполне устроят и медленные функции, которые просто работают. Мы можем запустить нашу программу на ночь, или запустить её утром, а результат получить через пару дней, если для нас это не критично, — можно не оптимизировать и оставить как есть.
Сколько стоит переписать старый код?
Важный вопрос, потому что мы живём не в мире розовых пони, а в мире реальных заказчиков, которые хотят не просто красивого кода, а прямой выгоды.
Сколько дополнительной памяти у нас есть?
Память во многих ситуациях используется недостаточно активно, притом что в данный момент времени у разработчика в распоряжении много ресурсов в плане дополнительной памяти. Значит, мы можем себе позволить какие-то предподсчёты хранить в самой программе и особо не заморачиваться. А вместо этого мы высчитываем одни и те же значения по много-много раз. Тут надо искать компромисс.
У меня есть любимый твит про преждевременную оптимизацию.

Никогда не трать 6 минут на то, чтобы сделать что-то руками, когда можешь потратить 6 часов, чтобы автоматизировать это
Да, преждевременная оптимизация действительно приводит к довольно неприятным последствиям.
Вроде как с длиной строк разобрались. Но её нам обычно недостаточно. Вот с чем ещё мы сталкиваемся.
Сравнение строк
Часто нам нужно сравнить строки. Есть две строки, хочется узнать, равны они или нет. Давайте на русском языке озвучим, как работал бы алгоритм сравнения строк, если бы его исполнял человек.
В этой ситуации мы тоже берём в руки карандаш и последовательно сверяем наши символы до тех пор, пока не встретим либо расхождение этих символов, либо не дойдём до конца строки и не обнаружим, что у нас две строки закончились одновременно.

И получается, что сравнение двух строк — линейное, не такая-то простая штука. Опять же, наша любимая «Война и мир», которую мы хотим сравнить с трудом такого же многословного писателя — это тоже будет линейная сложность. Можно ли это упростить?
Давайте посмотрим такую задачку. Подобное бывает на собеседованиях (по крайней мере, лично мне нравится её задавать).
У нас есть 100 строк, их надо разбить на группы. Если строки равны, они должны оказаться в одной группе, если разные — в разных.
Вот пример.

Слов существенно меньше, всего 7, 6 из них совершенно разные, 2 совпадают. Можно решить сортировкой, но есть и ещё варианты — подстрока.
Наивный вариант — то, что приходит в голову сразу же, когда мы пытаемся представить, как можно решить задачу.
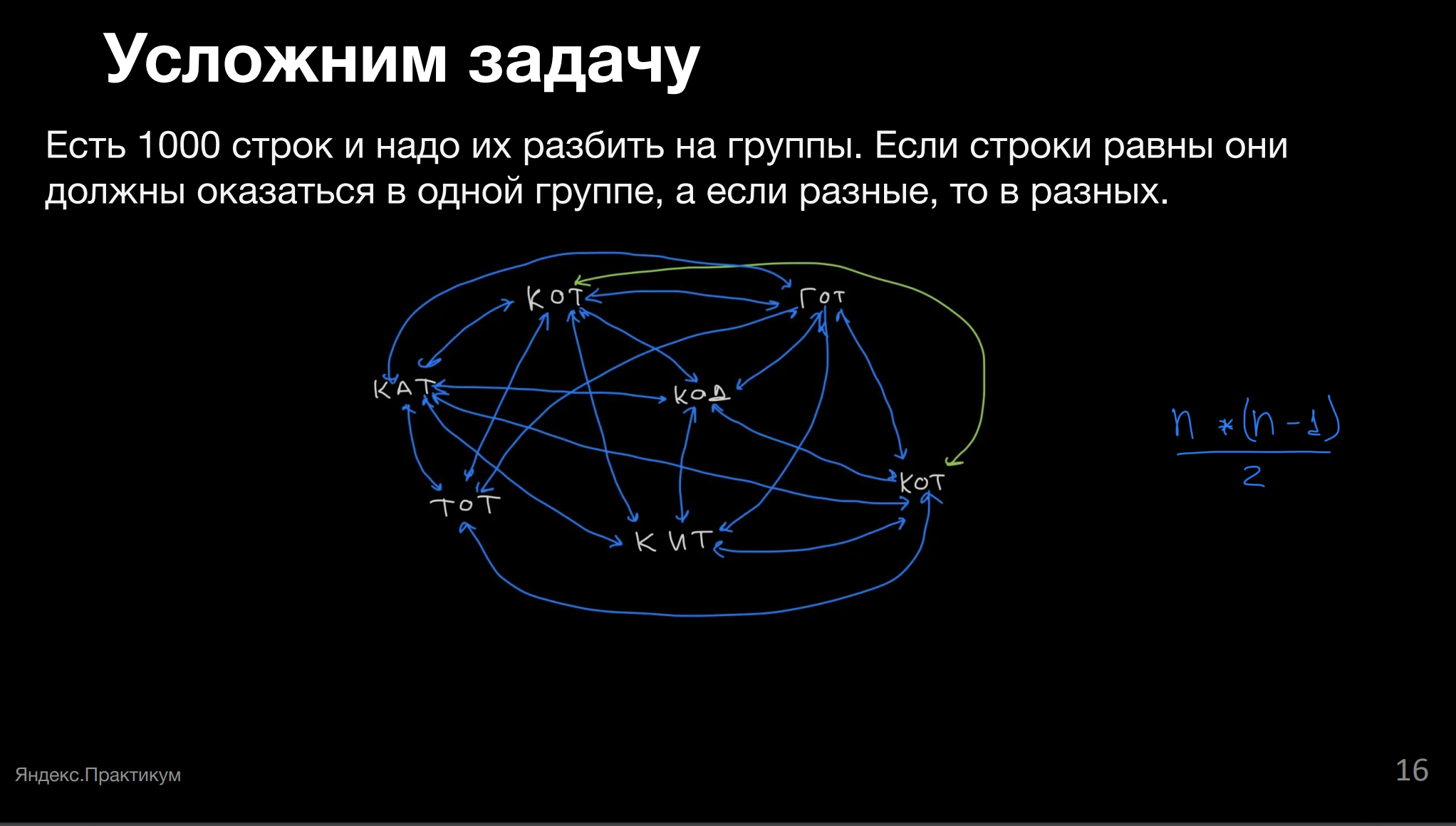
Самые внимательные заметят потерянные автором рисунка стрелочку и несколько запятых ;)
Берём и сравниваем между собой каждую пару слов, соответственно, проверяем, равны ли они между собой. Сколько будет сравнений?
N*N–1 / 2.
Берём N слов, связываем их со всеми остальными словами, которых N–1, и так, чтобы не сравнивать одно и то же слово дважды, делим пополам.
Как-то многовато выходит. А с учётом того, что каждое сравнение у нас происходит за какое-то линейное время от средней длины слова, получается совсем грустно. Это ведь у нас в примере слова короткие, 3 буквы, а если у нас слова будут очень длинные, то в этой истории можно и застрять.
Хочется сказать, что сложность кубическая, но давайте называть её кубической, чётко понимая, что N — это количество слов, а N», которое мы тут добавили как ещё один множитель, — это средняя длина строки. Тогда получим условно кубическую сложность.
У нас есть два основных варианта (но и множество других). Один вариант: мы сортируем, и слова, которые идут подряд, оказываются равны между собой.

Тут всё логично, они не могут оказаться не подряд. В этой сортировке происходит вот что: у нас есть совершенно разные сортировки. Многие (в худшем случае) работают за квадратичное время, и тут вроде как мы ничего и не улучшили. Но нас же никто не обязывает использовать квадратичную сортировку. ОК, у нас есть другие сортировки, которые работают чуть быстрее. А с учётом особенности входных данных при сортировке строк можно написать даже линейную сортировку.
Помимо этого есть встроенные возможности — хэшмапы, это когда у нас есть особая структура данных, которая умеет по ключу сохранять какое-то значение. Например, тут мы по ключу «Кот» добавили единичку, и мы знаем, что если раньше у нас «Кот» был один, то мы встретили ещё одного, и у нас их стало два. Тут важно на старте не пропустить инициализацию всего этого добра.
Здорово, вроде интересный вариант: мы за линейное время пробегаем и вычисляем.
Но вот хороший вопрос: каким образом понять, куда мы должны сохранять наше прекрасное слово? Неужели для того, чтобы найти место в массиве для сохранения значения для нашего кота, нам придётся перебрать все возможные значения в этом массиве?
Получается тоже не особо оптимистично, опять-таки квадрат.
А если придумать какое-то решение, которое позволит нам по изначальной строке узнавать, в какой ячейке она лежит?
Попробуем так: возьмём и будем суммировать, закодируем каждый символ алфавита в конкретную букву и просуммируем, получим что-то на выходе.

Итого мы поймём, что у нас есть много вариантов получения одной и той же строки. Тут вопрос даже не в обычной перестановке, abc можно переставить в bca и во что угодно, а то, что мы можем вообще обнаружить, что у нас разные буквы и разные длины этих строк.

А результирующий индекс получился одинаковый. Это нам не подходит.
Возьмем другой вариант построения такого числа. В чём суть: помимо того, что мы учитываем значение самой буквы, мы ещё учитываем и позицию, на которой она стоит. Для этого будем просто значение каждой буквы домножать на 10 и далее прибавлять.
Выглядит это так.

Тогда получится, что и старый вариант с одинаковой суммой всё ещё работает корректно, и вариант, где у нас просто перестановка, тоже в порядке.
Но и это не панацея. Может оказаться, что какая-то другая последовательность символов с домножением на 10 будет давать ту же сумму. Таких ситуаций меньше, но они всё ещё будут. Эта ситуация называется коллизией.
О том, как решать коллизии, мы довольно много говорим на курсе, тут же скажем, что они просто существуют, но будем верить, что живём в идеальном мире.
Итак, что произошло: мы научились брать и из исходного слова получать какое-то число, и по этому числу мы можем в нашем большом массиве записывать количество повторений конкретного слова.
Вроде бы не так плохо. Что у нас происходит в этом случае — получим массив, в котором будет шесть элементов, пять из которых будут заполнены единичками, а шестой — двоечкой.
Неплохой вариант, но для того, чтобы вычислить хэшкод нашей строки, нам всё равно надо линейно пробежаться по строке и посчитать какое-то число. С другой стороны, нам придётся сделать это по одному разу для каждого входного значения. В этом примере — семь раз и, соответственно, 7 умножить на тот самый N». Тогда был псевдокуб, так что это назовём псевдоквадратом.
Что нам это дало?
Что куб, что квадрат — штуки абстрактные, как и линейное время. Есть такое понятие как Flops, — это количество операций в секунду, которое может выполнить определённый компьютер. Я взяла в качестве примера характеристики Intel Core i7–5960X (Extreme Edition Haswell-E), 3,0 ГГц, 8 ядер (2014) из википедии.
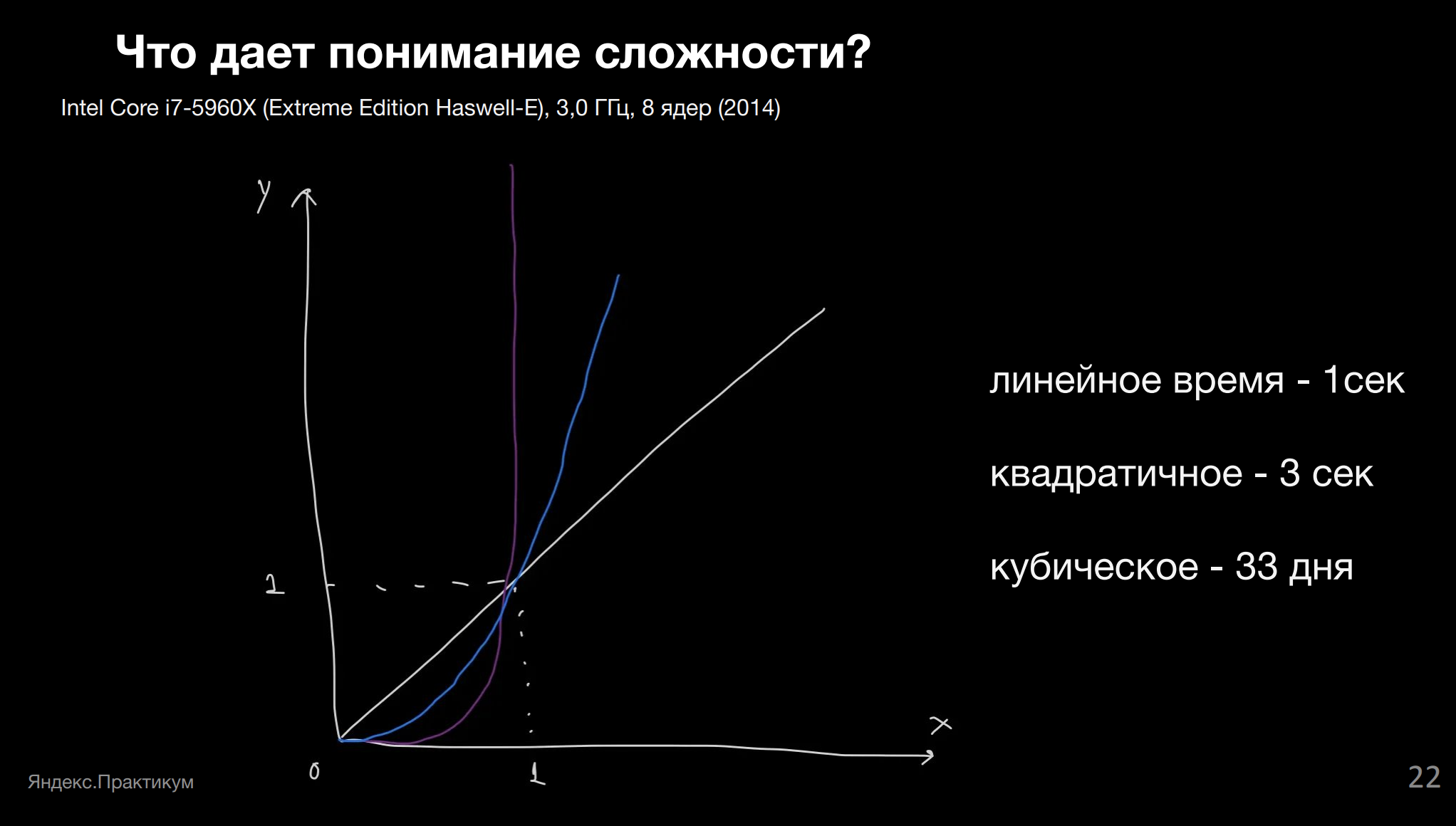
Предположим, что у нас миллион строк и разные варианты решения задачи.
Линейная сложность даст нам примерно секунду. Я не знаю, как решить эту задачу за линейное время. Квадратичная сложность даст уже три секунды. Не так круто, как одна, но не критично. А вот кубическая сложность даст уже 33 дня. И кажется, что на такое вряд ли какой разработчик пойдёт. Простой пример, но мы совершенно несложными упрощениями сократили время в тысячи раз.
Что ещё важно понимать про строки — иммутабельность, она же неизменяемость строк. Это применимо не ко всем языкам: у нас есть языки, в которых строки — изменяемые объекты, а есть те, в которых неизменяемые. Однако важно учесть, что эта изменяемость объектов тоже ограничена.

Когда у нас строки — изменяемые объекты, это значит, что мы можем исправить одну букву, как на картинке, заменить a на o — и всё работает. Но если мы захотим заменить не одну букву, а вместо одной буквы вставить, скажем, 15, добавить пропущенное слово, окажется, что все языки к нам не очень благосклонны, просто многие это усиленно скрывают.
Такое происходит потому, что у нас каждая строка — это массив либо байтов, либо символов. Соответственно, когда мы хотим что-то вставить в середину, надо раздвинуть соседние элементы: или те, что в конце, сдвинуть вправо, или те, что в начале, сдвинуть влево. На самом деле в большинстве языков это произойдёт таким образом — мы узнаем будущую длину итоговой строки и скажем: «Ага, чтобы её хранить, нам потребуется вот столько места». Поищем ближайшее место, где обнаружится столько символов + запас, скопируем все символы из старого места и переместим в новое.
Этот фокус сработает, но потребует времени. Мы его не заметим, но, если такое проделывать в цикле, окажется, что всё очень плохо, и у нас вроде программа-то элементарная, а тормозит дичайше.
Вспомните тот же ворд. Что там происходит, когда мы ставим курсор в середину и печатаем какую-то часть текста — неужели каждый набранный или удалённый символ передвигает целиковые массивы? И почему оно тогда не тормозит?
Чтобы понимать такие вещи, тоже полезно знать алгоритмы — насколько они показывают стандартные варианты решения проблем.
Например, можно реализовать хранение текста блоками. Тогда вместо того, чтобы считать наш текст единым неделимым блоком, мы будем считать, что это набор блоков, а изменения, которые мы вносим, — это изменения в одном блоке.
В процессе того, как мы эти изменения вносим, мы будем этот блок разбивать на подблоки, и в дальнейшем у нас окажется, что просто блоки идут друг за другом, а изменение одного блока никак не затрагивает другой. В итоге получится такой linked list, он же связный список.
Итак, со строками мы разобрались. Во второй части обсудим числа.
