Оптимизация кода: память
В действительности система памяти образует иерархию устройств хранения с разными ёмкостями, стоимостью и временем доступа. Регистры процессора хранят наиболее часто используемые данные. Маленькие быстрые кэш-памяти, расположенные близко к процессору, служат буферными зонами, которые хранят маленькую часть дынных, расположеных в относительно медленной оперативной памяти. Оперативная память служит буфером для медленных локальных дисков. А локальные диски служат буфером для данных с удалённых машин, связанных сетью.
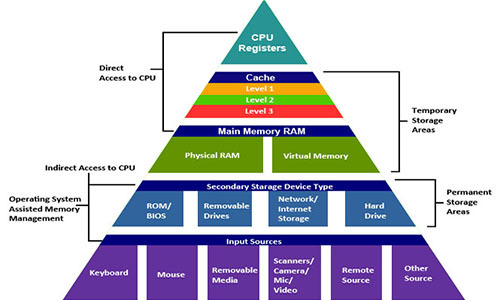
Иерархия памяти работает, потому что хорошо написанные программы имеют тенденцию обращаться к хранилищу на каком-то конкретном уровне более часто, чем к хранилищу на более низком уровне. Так что хранилище на более низком уровне может быть медленнее, больше и дешевле. В итоге мы получаем большой объём памяти, который имеет стоимость хранилища в самом низу иерархии, но доставляет данные программе со скоростью быстрого хранилища в самом верху иерархии.
Как программист, вы должны понимать иерархию памяти, потому что она сильно влияет на производительность ваших программ. Если вы понимаете как система перемещает данные вверх и вниз по иерархии, вы можете писать такие программы, которые размещают свои данные выше в иерархии, так что процессор может получить к ним доступ быстрее.
В этой статье мы исследуем как устройства хранения организованы в иерархию. Мы особенно сконцентрируемся на кэш-памяти, которая служит буферной зоной между процессором и оперативно памятью. Она оказывает наибольшее влияние на производительность программ. Мы введём важное понятие локальности, научимся анализировать программы на локальность, а также изучим техники, которые помогут увеличить локальность ваших программ.
На написание этой статьи меня вдохновила шестая глава из книги Computer Systems: A Programmer’s Perspective. В другой статье из этой серии, «Оптимизация кода: процессор», мы также боремся за такты процессора.
Память тоже имеет значение
Рассмотрим две функции, которые суммируют элементы матрицы. Они практически одинаковы, только первая функция обходит элементы матрицы построчно, а вторая — по столбцам.
int matrixsum1(int size, int M[][size])
{
int sum = 0;
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
sum += M[i][j]; // обходим построчно
}
}
return sum;
}
int matrixsum2(int size, int M[][size])
{
int sum = 0;
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
sum += M[j][i]; // обходим по столбцам
}
}
return sum;
}
Обе функции выполняют одно и то же количество инструкций процессора. Но на машине с Core i7 Haswell первая функция выполняется в 25 раз быстрее для больших матриц. Этот пример хорошо демонстрирует, что память тоже имеет значение. Если вы будете оценивать эффективность программ только в терминах количества выполняемых инструкций, вы можете писать очень медленные программы.
Данные имеют важное свойство, которое мы называем локальностью. Когды мы работаем над данными, желательно чтобы они находились в памяти рядом. Обход матрицы по столбцам имеет плохую локальность, потому что матрица хранится в памяти построчно. О локальности мы поговорим ниже.
Иерархия памяти
Современная система памяти образует иерархию от быстрых типов памяти маленького размера до медленных типов памяти большого размера. Мы говорим, что конкретный уровень иерархии кэширует или является кэшем для данных, расположенных на более низком уровне. Это значит, что он содержит копии данных с более низкого уровня. Когда процессор хочет получить какие-то данные, он их сперва ищет на самых быстрых высоких уровнях. И спускается на более низкие, если не может найти.
На вершине иерархии находятся регистры процессора. Доступ к ним занимает 0 тактов, но их всего несколько штук. Далее идёт несколько килобайт кэш-памяти первого уровня, доступ к которой занимает примерно 4 такта. Потом идёт пара сотен килобайт более медленной кэш-памяти второго уровня. Потом несколько мегабайт кэш-памяти третьего уровня. Она гораздо медленней, но всё равно быстрее оперативной памяти. Далее расположена относительно медленная оперативная память.
Оперативную память можно рассматривать как кэш для локального диска. Диски это рабочие лошадки среди устройств хранения. Они большие, медленные и стоят дёшево. Компьютер загружает файлы с диска в оперативную память, когда собирается над ними работать. Разрыв во времени доступа между оперативной памятью и диском колоссальный. Диск медленнее оперативной памяти в десятки тысяч раз, и медленнее кэша первого уровня в миллионы раз. Часто будет выгоднее обратиться несколько тысяч раз к оперативной памяти, чем один раз к диску. На это знание опираются такие структуры данных, как B-деревья, которые стараются разместить больше информации в оперативной памяти, пытаясь избежать обращения к диску любой ценой.
Локальный диск сам может рассматриваться как кэш для данных, расположенных на удалённых серверах. Когда вы посещаете веб-сайт, ваш браузер сохраняет изображения с веб-страницы на диске, чтобы при повторном посещении их не нужно было качать. Существуют и более низкие иерархии памяти. Крупные датацентры, типа Google, сохраняют большие объёмы данных на ленточных носителях, которые хранятся где-то на складах, и когда понадобятся, должны быть присоеденены вручную или роботом.
Современная система имеет примерно такие характеристики:
| Тип кэша | Время доступа (тактов) | Размер кэша |
|---|---|---|
| Регистры | 0 | десятки штук |
| L1 кэш | 4 | 32 KB |
| L2 кэш | 10 | 256 KB |
| L3 кэш | 50 | 8 MB |
| Оперативная память | 200 | 8 GB |
| Буфер диска | 100'000 | 64 MB |
| Локальный диск | 10'000'000 | 1000 GB |
| Удалённые сервера | 1'000'000'000 | ∞ |
Быстрая память стоит очень дорого, а медленная очень дёшево. Это великая идея архитекторов систем совместить большие размеры медленной и дешёвой памяти с маленькими размерами быстрой и дорогой. Таким образом система может работать на скорости быстрой памяти и иметь стоимость медленной. Давайте разберёмся как это удаётся.
Допустим, ваш компьютер имеет 8 ГБ оперативной памяти и диск размером 1000 ГБ. Но подумайте, что вы не работаете со всеми данными на диске в один момент. Вы загружаете операционную систему, открываете веб-браузер, текстовый редактор, пару-тройку других приложений и работаете с ними несколько часов. Все эти приложения помещаются в оперативной памяти, поэтому вашей системе не нужно обращаться к диску. Потом, конечно, вы закрываете одно приложение и открываете другое, которое приходится загрузить с диска в оперативную память. Но это занимает пару секунд, после чего вы несколько часов работаете с этим приложением, не обращаясь к диску. Вы не особо замечаете медленный диск, потому что в один момент вы работаете только с небольшим бъёмом данных, которые кэшируются в оперативной памяти. Вам нет смысла тратить огромные деньги на установку 1024 ГБ оперативной памяти, в которую можно было бы загрузить содержимое всего диска. Если бы вы это сделали, вы бы почти не заметили никакой разницы в работе, это было бы «деньги на ветер».
Так же дело обстоит и с маленькими кэшами процессора. Допустим вам нужно выполнить вычисления над массивом, который содержит 1000 элементов типа int. Такой массив занимает 4 КБ и полностью помещается в кэше первого уровня размером 32 КБ. Система понимает, что вы начали работу с определённым куском оперативной памяти. Она копирует этот кусок в кэш, и процессор быстро выполняет действия над этим массивом, наслаждаясь скоростью кэша. Потом изменённый массив из кэша копируется назад в оперативную память. Увеличение скорости оперативной памяти до скорости кэша не дало бы ощутимого прироста в производительности, но увеличило бы стоимость системы в сотни и тысячи раз. Но всё это верно только если программы имеют хорошую локальность.
Локальность
Локальность — основная концепция этой статьи. Как правило, программы с хорошей локальностью выполняются быстрее, чем программы с плохой локальностью. Локальность бывает двух типов. Когда мы обращаемся к одному и тому же месту в памяти много раз, это временнáя локальность. Когда мы обращаемся к данным, а потом обращаемся к другим данным, которые расположены в памяти рядом с первоначальными, это пространственная локальность.
Рассмотрим, программу, которая суммирует элементы массива:
int sum(int size, int A[])
{
int i, sum = 0;
for (i = 0; i < size; i++)
sum += A[i];
return sum;
}
В этой программе обращение к переменным sum и i происходит на каждой итерации цикла. Они имеют хорошую временную локальность и будут расположены в быстрых регистрах процессора. Элементы массива имеют плохую временную локальность, потому что к каждому элементу мы обращаемся только по разу. Но зато они имеют хорошую пространственную локальность — тронув один элемент, мы затем трогаем элементы рядом с ним. Все данные в этой программе имеют или хорошую временную локальность или хорошую пространственную локальность, поэтому мы говорим что программа в общем имеет хорошую локальность.
Когда процессор читает данные из памяти, он их копирует в свой кэш, удаляя при этом из кэша другие данные. Какие данные он выбирает для удаления тема сложная. Но результат в том, что если к данным обращаются часто, они имеют больше шансов оставаться в кэше. В этом выгода от временной локальности. Программе лучше работать с меньшим количеством переменных и обращаться к ним чаще.
Перемещение данных между уровнями осуществляется блоками определённого размера. К примеру, процессор Core i7 Haswell перемещает данные между своими кэшами блоками размером в 64 байта. Рассмотрим конкретный пример. Мы выполняем программу на машине с вышеупомянутым процессором. У нас есть массив v, содержащий 8-байтовые элементы типа long. И мы последовательно обходим элементы этого массива в цикле. Когда мы читаем v[0], его нет в кэше, процессор считывает его из оперативной памяти в кэш блоком размером 64 байта. То есть в кэш отправляются элементы v[0]–v[7]. Далее мы обходим элементы v[1], v[2], …, v[7]. Все они будут в кэше и доступ к ним мы получим быстро. Потом мы читаем элемент v[8], которого в кэше нет. Процессор копирует элементы v[8]–v[15] в кэш. Мы быстро обходим эти элементы и не находим в кэше элемента v[16]. И так далее.
Поэтому если вы читаете какие-то байты из памяти, а потом читаете байты рядом с ними, они наверняка будут в кэше. В этом выгода от пространственной локальности. Нужно стремиться на каждом этапе вычисления работать с данными, которые расположены в памяти рядом.
Желательно обходить массивы последовательно, читая его элементы один за другим. Если нужно обойти элементы матрицы, то лучше их обходить построчно, а не по столбцам. Это даёт хорошую пространственную локальность. Теперь вы можете понять, почему функция matrixsum1 работала медленнее функции matrixsum2. Двумерный массив расположен в памяти построчно: сначала расположена первая строка, сразу за ней идёт вторая и так далее. Первая функция читала элементы матрицы построчно и двигалась по памяти последовательно, будто обходила один большой одномерный массив. Эта функция в основном читала данные из кэша. Вторая функция переходила от строки к строке, читая по одному элементу. Она как бы прыгала по памяти слева-направо, потом возвращалась в начало и опять начинала прыгать слева-направо. В конце каждой итерации она забивала кэш последними строками, так что в начале следующей итерации первых строк кэше не находила. Эта функция в основном читала данные из оперативной памяти.
Дружелюбный к кэшу код
Как программисты вы должны стараться писать код, который, как говорят, дружелюбный к кэшу (cache-friendly). Как правило, основной объём вычислений производится лишь в нескольких местах программы. Обычно это несколько ключевых функций и циклов. Если есть вложенные циклы, то внимание нужно сосредоточить на самом внутреннем из циклов, потому что код там выполняется чаще всего. Эти места программы и нужно оптимизировать, стараясь улучшить их локальность.
Вычисления над матрицами очень важны в приложениях анализа сигналов и научных вычислениях. Если перед программистами встанет задача написать функцию перемножения матриц, то 99.9% из них напишут её примерно так:
void matrixmult1(int size, double A[][size], double B[][size], double C[][size])
{
double sum;
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++) {
sum = 0.0;
for (int k = 0; k < size; k++)
sum += A[i][k]*B[k][j];
C[i][j] = sum;
}
}
Этом код дословно повторяет математическое определение перемножения матриц. Мы обходим все элементы окончательной матрицы построчно, вычисляя каждый из них один за другим. В коде есть одна неэффективность, это выражение B[k][j] в самом внутреннем цикле. Мы обходим матрицу B по стобцам. Казалось бы, ничего с этим не поделаешь и придётся смириться. Но выход есть. Можно переписать то же вычисление по другому:
void matrixmult2(int size, double A[][size], double B[][size], double C[][size])
{
double r;
for (int i = 0; i < size; i++)
for (int k = 0; k < size; k++) {
r = A[i][k];
for (int j = 0; j < size; j++)
C[i][j] += r*B[k][j];
}
}
Теперь функция выглядит очень странно. Но она делает абсолютно то же самое. Только мы не вычисляем каждый элемент окончательной матрицы за раз, мы как бы вычисляем элементы частично на каждой итерации. Но ключевое свойство этого кода в том, что во внутреннем цикле мы обходим обе матрицы построчно. На машине с Core i7 Haswell вторая функция работает в 12 раз быстрее для больших матриц. Нужно быть действительно мудрым программистом, чтобы организовать код таким образом.
Блокинг
Существует техника, которая называется блокинг. Допустим вам надо выполнить вычисление над большим объёмом данных, которые все не помещаются в кэше высокого уровня. Вы разбиваете эти данные на блоки меньшего размера, каждый из которых помещается в кэш. Выполняете вычисления над этими блоками по отдельности и потом объёдиняете результат.
Можно продемонстрировать это на примере. Допустим у вас есть ориентированный граф, представленный в виде матрицы смежности. Это такая квадратная матрица из нулей и единиц, так что если элемент матрицы с индексом (i, j) равен единице, то существует грань от вершины графа i к вершине j. Вы хотите превратить этот ориентированный граф в неориентированный. То есть, если есть грань (i, j), то должна появиться противоположная грань (j, i). Обратите внимание, что если представить матрицу визуально, то элементы (i, j) и (j, i) являются симметричными относительно диагонали. Эту трансформацию нетрудно осуществить в коде:
void convert1(int size, int G[][size])
{
for (int i = 0; i < size; i++)
for (int j = 0; j < size; j++)
G[i][j] = G[i][j] | G[j][i];
}
Блокинг появляется естественным образом. Представьте перед собой большую квадратную матрицу. Теперь иссеките эту матрицу горизонтальными и вертикальными линиями, чтобы разбить её, скажем, на 16 равных блока (четыре строки и четыре столбца). Выберите два любых симметричных блока. Обратите внимание, что все элементы в одном блоке имеют симметричные элементы в другом блоке. Это наводит на мысль, что ту же операцию можно совершать над каждым блоком поочерёдно. В этом случае на каждом этапе мы будем работать только с двумя блоками. Если блоки сделать достаточно маленького размера, то они поместятся в кэше высокого уровня. Выразим эту идею в коде:
void convert2(int size, int G[][size])
{
int block_size = size / 12; // разбить на 12*12 блоков
// представим, что делится без остатка
for (int ii = 0; ii < size; ii += block_size) {
for (int jj = 0; jj < size; jj += block_size) {
int i_start = ii; // индекс i для блока принимает значения [ii, ii + block_size)
int i_end = ii + block_size;
int j_start = jj; // индекс j для блока принимает значения [jj, jj + block_size)
int j_end = jj + block_size;
// обходим блок
for (int i = i_start; i < i_end; i++)
for (int j = j_start; j < j_end; j++)
G[i][j] = G[i][j] | G[j][i];
}
}
}
Нужно заметить, что блокинг не улучшит производительность на системах с мощными процессорами, которые хорошо делают предвыборку. На системах, которые не делают предвыборки, блокинг может сильно увеличить производительность.
На машине с процессором Core i7 Haswell вторая функция не выполняется быстрее. На машине с более простым процессором Pentium 2117U вторая функция выполняется в 2 раза быстрее. На машинах, которые не выполняют предвыборку, производительность улучшилась бы ещё сильнее.
Какие алгоритмы быстрее
Все знают из курсов по алгоритмам, что нужно выбирать хорошие алгоритмы с наименьшей сложностью и избегать плохих алгоритмов с высокой сложностью. Но эти сложности оценивают выполнение алгоритма на теоретической машине, созданной нашей мыслью. На реальных машинах теоретически плохой алгоритм может выполнятся быстрее теоретически хорошего. Вспомните, что получить данные из оперативной памяти занимает 200 тактов, а из кэша первого уровня 4 такта — это в 50 раз быстрее. Если хороший алгоритм часто трогает память, а плохой алгоритм размещает свои данные в кэше, хороший может выполняться медленнее плохого. Также хороший алгоритм может хуже выполняться на процессоре, чем плохой. К примеру, хороший алгоритм вносит зависимость данных и не может загрузить конвеер, а плохой лишён этой проблемы и на каждом такте отправляет в конвеер новую инструкцию. Иными словами, сложность алгоритма это ещё не всё. То, как алгоритм будем выполняться на конкретной машине с конкретными данными, имеет значение.
Представим, что вам нужно реализовать очередь целых чисел, и новые элементы могут добавляться в любую позицию очереди. Вы выбираете между двумя реализациями: массив и связный список. Чтобы добавить элемент в середину массива, нужно сдвинуть вправо половину массива, что занимает линейное время. Чтобы добавить элемент в середину списка, нужно дойти по списку до середины, что также занимает линейное время. Вы думаете, что раз сложности у них одинаковые, то лучше выбрать список. Тем более у списка есть одно хорошее свойство. Список может расти без ограничения, а массив придётся расширять, когда он заполнится. Давайте представим что длина очереди 1000 элементов и нам нужно вставить элемент в середину очереди. Элементы списка хаотично разбросаны по памяти, а получить данные из памяти занимает 200 тактов. Поэтому чтобы обойти 500 элементов, нам понадобится 500×200=100'000 тактов. Массив расположен в памяти последовательно, что позволит нам наслаждаться скоростью кэша первого уровня с временем доступа 4 такта. Используя несколько оптимизаций, мы можем двигать элементы, тратя 1–4 такта на элемент. Мы сдвинем половину массива максимум за 500×4=2000 тактов. Это быстрее в 50 раз.
Если в предыдущем примере все добавления были бы в начало очереди, реализация со связным списком была бы более эффективной. Если какая-то доля добавлений была бы куда-то в середину очереди, реализация в виде массива могла бы стать лучшим выбором. Мы бы тратили такты на одних операциях и экономили такты на других операциях. И в итоге могли бы остаться в выигрыше. Нужно учитывать все аспекты каждой конкретной ситуации.
Заключение
Система памяти организована в виде иерархии устройств хранения с маленькими и быстрыми устройствами вверху иерархии и большими и медленными устройствами внизу. Программы с хорошей локальностью работают с данными из кэшей процессора. Программы с плохой локальностью работают с данными из относительно медленной оперативной памяти.
Программисты, которые понимают природу иерархии памяти, могут структурируют свои программы так, чтобы данные располагались как можно выше в иерархии и процессор получал их быстрее.
В частности, рекомендуются следующие техники:
- Сконцентрируйте ваше внимание на внутренних циклах. Именно там происходит наибольший объём вычислений и обращений к памяти.
- Постарайтесь максимизировать пространственную локальность, читая объекты из памяти последовательно, в том порядке, в котором они в ней расположены.
- Постарайтесь максимизировать временную локальность, используя объекты данных как можно чаще после того, как они были прочитаны из памяти.
Комментарии (5)
10 октября 2016 в 18:35
0↑
↓
Статья хорошая и полезная, но некоторые утверждения меня смущают.> «Часто будет выгоднее обратиться 100'000 раз к оперативной памяти, чем 1 раз к диску.»
Но ведь 100.000 обращений к оперативной памяти делается операциями, которые сами по себе займут 100.000 * x тактов? Как часто можно встретить ситуацию, когда 100.000 раз обращений к оперативки выгоднее, чем одно обращение к диску, особенно учитывая существование SSD и PCI-SSD?
> Скорость обращения к удаленному серверу »1'000'000'000 тактов»
Как можно скорость отклика (ping) мерять тактами? Тем более, что сетевой сокет в гигабитной локалке, может быть быстрее, чем обращение к диску. Я могу расшарить на соседнем компе виртуальный ram-диск, и по гигабитной сети это будет совсем не 1.000.000.000 тактов.
10 октября 2016 в 18:51
0↑
↓
Учитывается, что оперативная память хорошо кэшируется. 100'000 раз считать из L1 кэша займёт 0.4М тактов, а раз считать с диска 10М тактов.10 октября 2016 в 19:01
0↑
↓
то есть прокрутить цикл на 100.000 итераций быстрее, чем один раз обратиться к диску?
Мы же не считаем непосредственно доступ к памяти, а учитываем количество обращений со всем прилагаемым — сами операции обращения?
10 октября 2016 в 18:55
0↑
↓
А по поводу чтения из сети, это же всё приблизительно. Это общая картина.
10 октября 2016 в 18:59
0↑
↓
Одна кликабельная картинка лучше тысячи слов!
