Одна задача про кактус-граф12.04.2017 17:04

Начинается пора вступительных экзаменов, а значит и решения интересных задач. Пару лет назад Computer Science Center предлагал поступающим разобраться с задачей про кактус-граф, и сегодня речь пойдёт именно о ней. Попробуйте подумать над задачей сами, а затем свериться с решением.


К слову, набор в CS центр уже идёт. В этом году поступить на очное обучение можно не только в Санкт-Петербурге, но и в Новосибирске. Приходите — на занятиях ещё больше интересного.


Чуть больше про CS центр и набор

Computer Science Center — это совместная инициатива Computer Science клуба при ПОМИ, компании JetBrains и Школы анализа данных Яндекса. Центр предлагает двух- или трёхлетние курсы для студентов, аспирантов и выпускников технических вузов, а также молодых специалистов, желающих развиваться в области анализа данных, разработки ПО или теоретической информатики. Занятия проходят по вечерам в Санкт-Петербурге или в Новосибирске.


В 2017 году набор на очное обучение состоит из четырёх этапов:


  • подача заявки до 16 апреля включительно,
  • онлайн-тестирование,
  • экзамен,
  • очное собеседование.

Задача


Кактусом называется простой связный граф, в котором любые два цикла имеют не больше одной общей вершины. Доказать, что максимальное число ребер в кактусе с n вершинами равно $\operatorname{floor}\frac{3}{2}(n-1)$.


*$\operatorname{floor}$ — округление вниз.


Решение


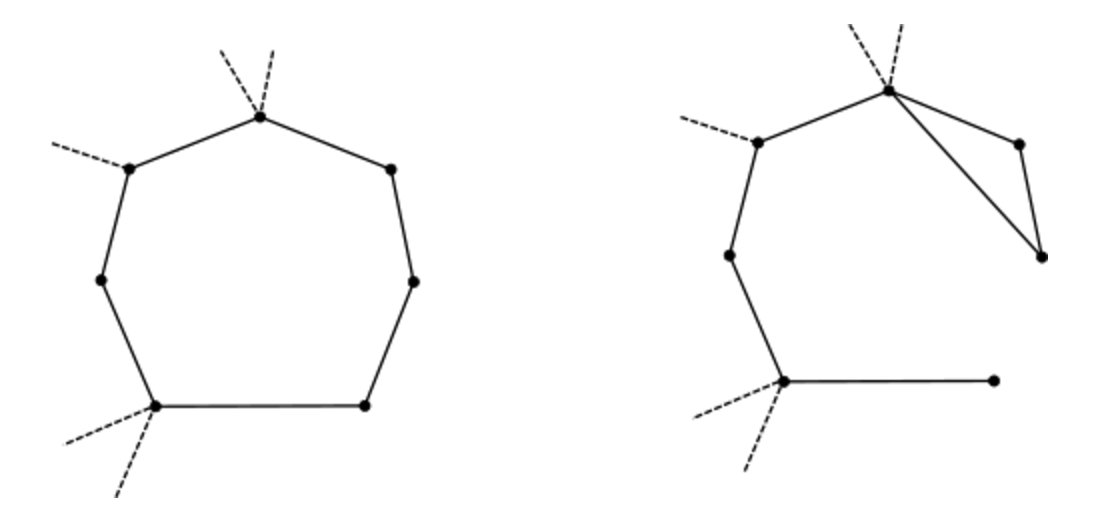
Сначала нужно понять, как этот граф устроен. Поможет нам в этом пример графа, изображённого на рисунке. Рядом изображён настоящий кактус. Это позволяет понять, чем обусловлено такое название.


5bc08b6bee284bc0ae40c9a77f53de42.png

Любой цикл, в котором больше трёх вершин, можно «затянуть», заменив на цикл длины три и простой путь. При этом общее число вершин и рёбер в графе не изменится, а сам граф останется кактусом. Ниже пример «затягивания» графа.


b9024fa5089b47c78b113910b14dcd02.png

Рассмотрим теперь кактус, в котором найдутся рёбра, не лежащие ни на одном цикле. Любые два таких ребра можно стянуть в вершину. В результате из графа исчезнут два ребра и две вершины. После чего добавить в граф цикл длины три, одна из вершин которого будет уже существующей вершиной графа. Количество вершин станет прежним, а число ребер увеличится на единицу.


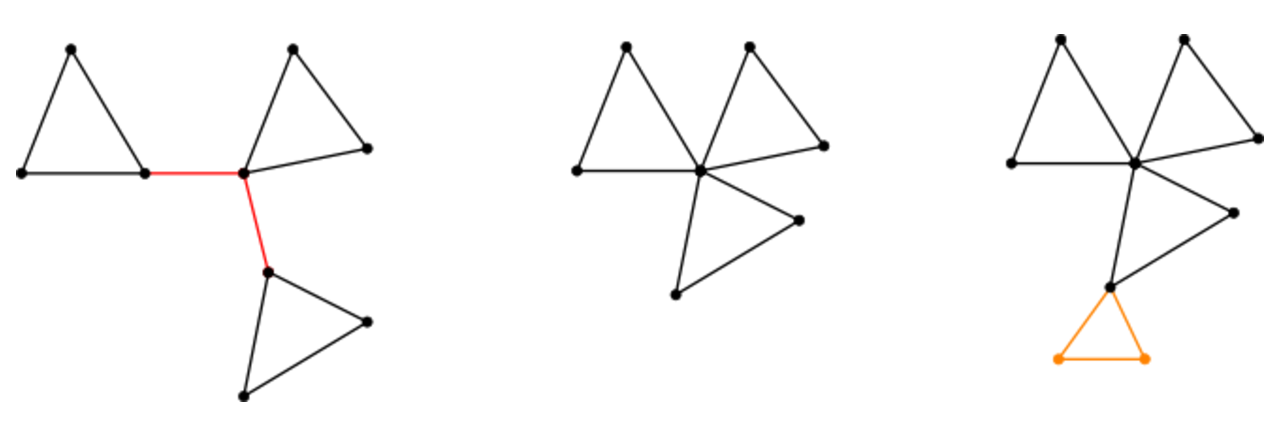
20b1d7768912413bbbec60e76f99e549.png

На рисунке выше изображён пример описанной выше манипуляции. На левом рисунке изображён кактус, в котором выделены ребра вне циклов. На центральном рисунке тот же кактус, но уже со стянутыми ребрами. В нём не только исчезли два ребра, но и стало на две вершины меньше. И, наконец, на правом рисунке изображен кактус, к которому мы прибавили ещё один треугольник, — появились три новых ребра и две вершины. В результате количество вершин до и после операции не изменилось, а количество рёбер увеличилось.


Таким образом, максимальное количество рёбер в кактусе достигается тогда, когда он состоит целиком из треугольников и, может быть, одного ребра, не лежащего ни на одном цикле. Такой кактус можно построить последовательным добавлением крайних блоков-треугольников, начав либо с $K_3$, либо с $K_2$, в зависимости от чётности $n$. ($K_n$ — полный граф на $n$ вершинах.) При добавлении каждого блока добавляется две вершины и три ребра, откуда немедленно следует требуемое в задаче утверждение.

Комментарии (1)

  • 12 апреля 2017 в 15:53 (комментарий был изменён)

    0

    ↑

    ↓

    Спасибо за статью. У меня вопрос: термин «затягивание графа» был придуман Вами именно для этой статьи? Т.к. гугление данного термина такого понятия не показало, а термин стягивание графа — это не то, что Вы здесь используете (при стягивании цикла нельзя получить ничего кроме цикла пока количество вершин результирующего цикла больше двух).


    Если же термин «затягивание графа» существует — пожалуйста дайте указание «где посмотреть».

© Habrahabr.ru