Обзор дескрипторов изображения Local Binary Patterns (LBP) и их вариаций
Добрый день, хабровчане. Приглашаю под кат программистов, интересующихся компьютерным зрением и обработкой изображений. Возможно, вы пропустили несложный, но эффективный математический инструмент для низкоуровневого описания текстур и задания их признаков для алгоритмов машинного обучения.
Введение
Тема LBP уже поднималась на Хабре, тем не менее, я решил немного распространить предложенное объяснение и поделиться некоторыми вариациями этого паттерна.
Как известно, компьютерное изображение — это та же числовая информация. Каждый пиксел представляется числом в случае чёрно-белого изображения или тройкой чисел в случае цветного. В целом они составляют приятную картинку для человеческого глаза и над ними удобно проводить преобразования, но зачастую информации оказывается слишком много. Например, в задачах распознавания объектов нас редко интересует значение каждого пикселя по отдельности: изображения часто зашумлены, да и искомые образы могут представать в разных вариантах, поэтому желательно, чтобы алгоритмы обладали устойчивостью к погрешностям, умению ухватить общий тренд. Это свойство англоязычные источники называют робастностью (robustness).
Один из способов разделаться с этой проблемой — предварительно обработать изображение, и оставить только значимые точки, а уже к ним применять последующие алгоритмы. Для этого придуманы SIFT, SURF и прочие DAISY, дескрипторы особенностей. С их помощью можно сшивать картинки, сопоставлять объекты и делать много чего полезного, однако у этих дескрипторов есть свои недостатки. В частности, ожидается, что найденные точки будут в некотором смысле действительно особенными и уникальными, воспроизводящимися от изображения к изображению. Не стоит использовать SIFT, чтобы понять, что обе половины этого изображения это кирпичные стены.

Кроме того, хоть эти дескрипторы и называются локальными, они всё-таки используют довольно значительную область изображения. Это нехорошо с точки зрения затрат на вычисление. Давайте немного ослабим это положение. Быть может, у нас получится характеризовать изображение, рассматривая ещё более маленькие структуры?
Основная идея
Повторюсь, мы хотим получить способ описать структуру картинки, который
- Быстро считается
- Инвариантен при преобразованиях яркости, сохраняющих порядок (
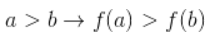 )
) - Устойчив к шумам
- Устойчив к вариациям текстуры
- Сильно уменьшает размерность задачи
Так что же такое Local Binary Pattern? Вкратце: это способ для каждого пикселя описать, в каком направлении убывает яркость. Построить его совсем несложно. Давайте этим и займёмся.
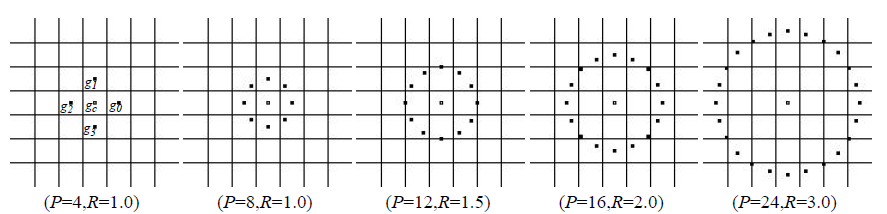
- Для начала следует выбрать радиус и количество точек… стоп-стоп, кто сказал «жулик»? Да, буквально парой строчек выше я написал, что этот дескриптор очень локальный, но определение того, что есть «очень локальное» может разниться от изображения к изображению. Но так уж и быть, давайте остановимся на радиусе в единицу: здесь и далее для каждого пикселя будем считать LBP на основе 8 смежных точек.
- Пронумеровать выбранные точки.
- Вычислить разность значений яркости между каждым из крайних пикселей и центральным.
- Если разность отрицательная (яркость убывает) записать в уме на месте соседа единицу, если неотрицательная (>=0) — ноль.
- «Вытянуть» образовавшуюся окружность из нулей и единиц в линию.
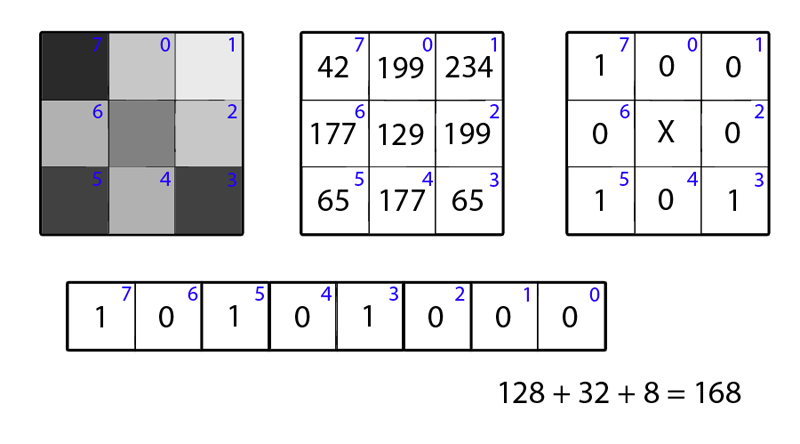
Секундочку, да это же просто двоичное число! Его-то мы и назовём умными словами Local Binary Pattern (Timo Ojala, Июль 2002). С точки зрения математики это выглядит так: 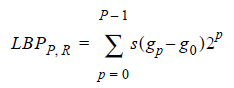
Вот и всё. Более подкованный в математике читатель назовёт биты дескриптора знаками производных яркости по направлениям, но это непринципиально. Понятно, что требования 1–2 тривиально выполняются. 3, наверное, требует доработки, об этом мы поговорим чуть позже. Но что делать с 4? Пока что не совсем понятно, как с этим работать. Да и с уменьшением размерности задачи мы справились так себе: вместо байта значений яркости пикселя мы получили байт знаков изменения яркости по направлениям. Инвариантности по аффинным преобразованиям нет, но мы её и не требовали: в конце концов, узор из квадратов и из ромбов — это два разных узора.
Из полученных данных уже можно извлечь что-нибудь интересное, давайте поскорее посмотрим, как применить их на практике, и, исходя из этого, подумаем, как их улучшить.
Хорошо, я научился считать LBP. Что дальше?
Используйте LBP, где идёт работа с текстурами. Самый банальный вариант: на вход программе подаётся текстура, и она определяет, текстура чего перед ней. Это может быть одним из шагов или вспомогательным средством более сложного алгоритма. Например, алгоритма распознавания на изображении объекта, не обладающего определённой формой, а только некоей структурой: огня, дыма или листвы (Hongda Tian, 2011). Альтернативный вариант: использовать LBP при сегментировании изображений, чтобы научить машину считать уникальным объектом не каждую полосу на зебре, а всю зебру целиком. Видеть за деревьями лес.
Как именно это происходит зависит от задачи и выбранного вида LBP. Далеко не всегда имеет смысл искать на картинках повторяющиеся узоры из LBP, и уж точно не следует сопоставлять дескрипторы на одном изображении с дескрипторами на другом. Устойчивость к шумам мы планируем взять количеством, и это играет с нами злую шутку: получившихся кодов попросту слишком много. Хорошие результаты можно получить, если подключить к карте LBP нейронную сеть-автокодировщик (autoencoder), из подготовленных паттернов она сможет извлечь больше информации, чем из сырой картинки. Более простой вариант — сгрести все получившиеся коды в одну кучу (построить гистограмму), и работать уже с ней.
Последний подход поначалу выглядит странно. Не теряется ли информация, когда мы так просто стираем информацию о взаимном расположении микроэлементов изображения? Вообще, да, возможно подобрать пример из трёх картинок, что 1 и 2 визуально больше похожи, но по гистограмме более схожими оказываются 1 и 3, однако, на практике такое маловероятно.
Полная гистограмма тоже часто несёт избыточную информацию, поэтому посоветую вооружиться приёмом, предложенным в (S. Liao, May 2009) и развитым в (Jinwang Feng, 2015):
- Вычисляете дескрипторы для каждого пикселя на изображении
- Считаете их гистограмму
- Сортируете бины гистограммы по убыванию. На удивление, как утверждают (S. Liao, May 2009), информацию, какие именно это бины, можно отбросить, само распределение их по гистограмме несёт достаточно информации. Можно и не отбрасывать, на мой взгляд, так надёжнее.
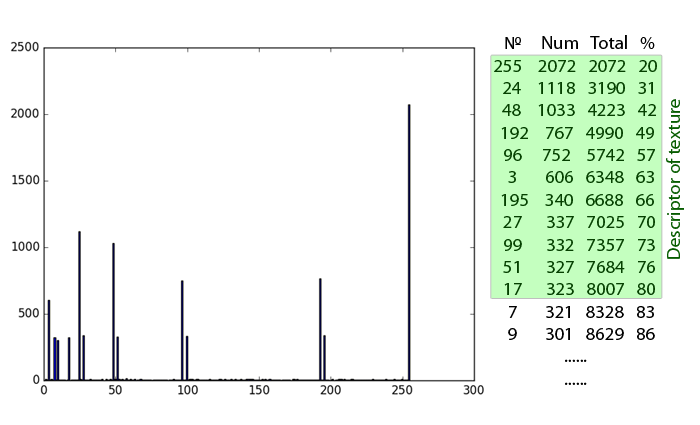
- Оставляете часть гистограммы, которая включает некоторый заранее определённый процент паттернов, остальное отбрасываете. Графики в той же работе утверждают, что 80% — приемлемое число. Оставленный кусок распределения ([номер бина], его процентное количество) — это так называемые доминантные паттерны (DLBP).
- DLBP можно скормить нейронной сети или SVM, которая при помощи магии машинного обучения и заранее предоставленной учебной выборки определит, что же за текстура перед ней.
В заключение, отмечу, что никто не заставляет вас зацикливаться на текстурах. LBP c успехом применяются вместо и вместе с Хаар-подобными признаками при AdaBoost-обучении. Они захватывают высокочастотную информацию, которую пропускают интегральные признаки.
Вариации
Пока что выбор LBP в качестве низкоуровневой информации для машинного обучения выглядит неубедительно. Самое время исправить недостатки, о которых мы говорили выше! Для такого на удивление простого дескриптора как LBP за время его существования придумано множество вариаций.
Перед нами стоят две противоречащие друг другу задачи. Первая: уменьшить количество паттернов, чтобы их было легче пережёвывать машине. Часто нас интересуют гистограммы, и если гистограмма из 2^8 элементов это приемлемо, то из 2^24 занимает уже многовато места. Вторая: увеличить информативность паттернов. Нам бы хотелось различать особые точки разного типа, причём, чем сильнее они отличаются, тем сильнее должны отличаться паттерны. Отдельным пунктом следует внести устойчивость к шуму.
Значимые паттерны
Для начала заметим, что интереснее всего для нас объекты, которые может опознать и человеческий глаз: границы линий, углы, точки или пятна. Если мысленно поместить центральную точку на край такого объекта и посчитать LBP, то на этапе окружности можно увидеть, что нули и единицы как бы разделяются на две группы. При «вытягивании» окружности образуется число с 0, 1 или 2 переходами 0–1 или 1–0. Например,»00111100»,»11111111» и »01111111» — относятся к «хорошим» паттернам, а »10100000» и »01010101» — нет.
Порадуемся. Хотя не то чтобы мы единственные, кто это обнаружил. В работе, с которой началось активное исследование LBP (Timo Ojala, Июль 2002), тоже заметили, что такие паттерны несут большую часть значимой информации. Для них даже придумали специальное название: «униформные паттерны» (uniform patterns). Их количество несложно посчитать: для 8 соседей имеем 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 1 = 37 штук ((P+1)*P/2 + 1). Плюс ещё одна метка, под которую сгребём все не-униформные паттерны. Стало намного приятнее.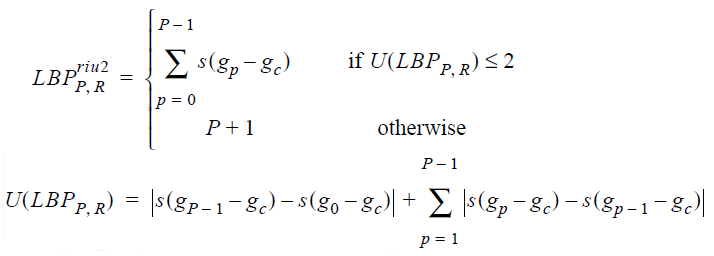
Существуют и другие способы проредить набор меток. Например, если мы по каким-то причинам не хотим убирать не-униформные паттерны, мы можем хотя бы избавиться от всех паттернов, получающихся поворотами изображения вокруг центрального пикселя. Достаточно ввести однозначное соответствие, которое будет отображать группу LBP в один. Скажем, будем считать «настоящим» паттерном тот, который имеет минимальное значение при циклических сдвигах вправо. Или влево. В подарок достаётся инвариантность дескриптора относительно вращения объекта. (Junding Sun, 2013)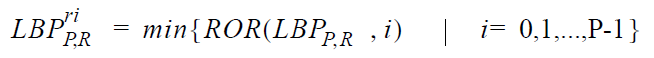
Ещё можно принять одинаковыми паттерны, для случаев, когда объект и фон меняются цветами. Тогда можно считать за «эффективный» паттерн минимум из LBP и ~LBP. Этот вариант использовался в работе по детектированию дыма, который может выглядеть светло-серым на тёмном фоне или тёмно-серым на белом фоне (Hongda Tian, 2011).
В (Yiu-ming Cheung, 2014) вообще предлагается избавиться от лишних соседей и считать ультралокальные дескрипторы, используя только по паре-тройке пикселей, а затем «собирать» особенности подсчётом матриц совпадений (co-occurrence matrix), но это больше походит на обычное вычисление производной c последующими махинациями над ней. Мне кажется, их сложно эффективно применить на практике.
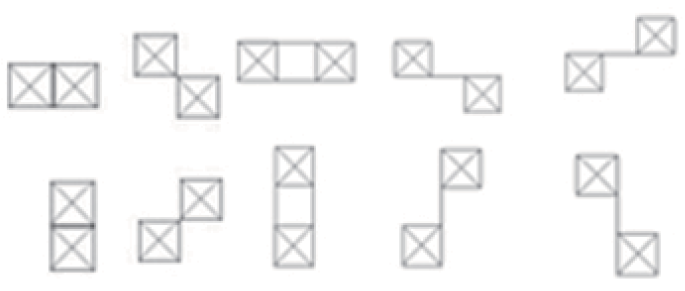
Как вариант, можно рассматривать производную яркости второго порядка, ей нужно всего 4 направления. К сожалению, она более склонна к негативному влиянию шума, и с меньшей вероятностью несёт значимую информацию об изображении. Применение этой техники тоже сильно зависит от задачи.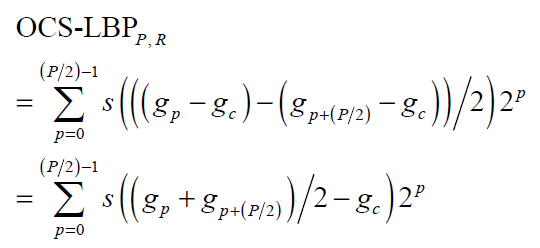
Устойчивость к шуму
Но вообще идея насчёт изменения способа, которым мы считаем производную, была хорошей. Попробуем вернуться к первой производной и ввести более строгие ограничения на перемену её знака. Будем рассматривать не направления из центрального пикселя в крайние, а направления из крайних пикселей в дальние от него крайние (Junding Sun, 2013).
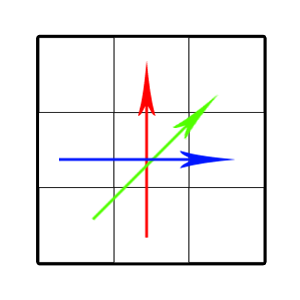
Будем писать единицу для пикселя, если яркость уменьшается из первого пикселя в центральный и из центрального — во второй. Если яркость возрастает или не имеет определённого поведения — ноль. К сожалению, мы теряем информацию о ярких и тёмных одиноких точках, но если мы знаем, что изображение содержит сильный шум, это даже хорошо.
Вообще, если ожидается высокий уровень шума, можно использовать больше точек для вычисления производной, усреднять с некоторыми весами с значениями соседей или даже значениями пикселей за пределами выбранного круга.
Способ, которым мы проверяем, изменяется ли яркость, тоже кажется немного подозрительным. В самом деле, если использовать просто знак производной, то LBP будет находить фантомные узоры даже на абсолютно гладком изображении при наличии даже минимального шума. Обычный способ расправиться с такой проблемой — установить пороговое значение, с которым мы сравниваем изменение яркости между пикселями. Можно задать его извне, если есть дополнительная информация о характере изображения, но это не слишком здорово, так как начинается типичное гадание на параметрах. Более предпочтительный вариант — посчитать среднее значение производной по некоторой окрестности или всему изображению и сравнивать уже с ним (Jinwang Feng, 2015).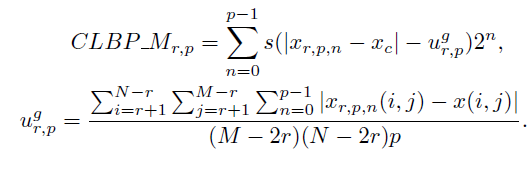
При желании можно использовать больше градаций, но это раздувает максимальное количество паттернов.
Больше информации
Local Binary Pattern несложно распространить на случай трёх измерений (Xiaofeng Fu, 2012), (Guoying Zhao, 2007), (Xie Liping, July 2014). Если представить видео, как «стопку» кадров, то у каждого пикселя оказывается не 8, а 9+9+8=26 соседей (или меньше, если убрать некоторые угловые пиксели). Существуют разные способы получения LBP в этом случае. Два самых распространённых:
- Три параллельных плоскости. Для каждого пикселя i, j считаем по стандартной LBP в кадрах t-1, t, t+1. После чего конкатенируем их и записываем, либо, если нас интересуют только паттерны, не меняющиеся от кадра к кадру, сравниваем их между собой, и пишем только если получившиеся LBP одинаковые, иначе присваиваем «мусорную» метку.
- Три ортогональных плоскости. Для каждого пикселя (i, j, t) рассматриваем три набора соседей: лежащие в кадре, разные по времени, одинаковые по ряду, разные по времени одинаковые по столбцу. Этот способ больше подходит для изменяющихся с течением времени паттернов. Он требует больших вычислительных затрат, чем предыдущий.
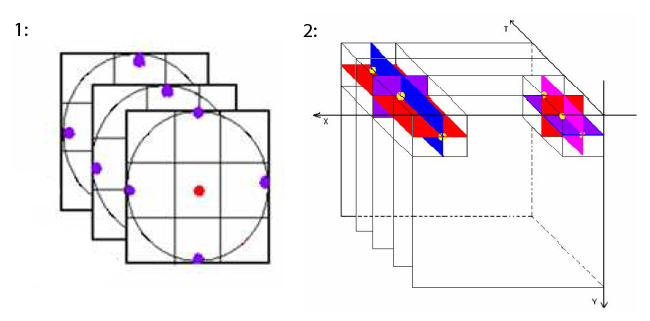
Наконец, к дескриптору можно прикрепить результат какого-нибудь нелокального фильтра. Например, в (Xie Liping, July 2014) для этого используются фильтры Габора. Они хорошо подходят для обнаружения периодических структур, но обладают определёнными недостатками, в частности, «звонят» на одиноких прямых. Правильное комбинированное применение LBP и глобальных фильтров позволяет избавиться от минусов и тех и тех. На Хабре про применение фильтров Габора можно почитать, например, здесь и здесь.
Пример
Практика без теории слепа, но теория без практики и вовсе мертва, так что давайте что-нибудь уже запрограммируем. Этот тривиальный код на Python 3.4 (требуются PIL, numpy и matplotlib) считает и выводит гистограмму LBP для изображения. Для простоты понимания использовалась только оптимизация с установкой минимальной разницы в яркости пропорциональной средней разнице в яркости по изображению. Из результата можно вычислить и использовать для машинного обучения DLBP, но в целом, это очень наивная реализация. В реальных применениях изображению необходима предобработка. Обратите внимание, что нули, дескрипторы однородной области, не записываются: их почти всегда очень-очень много и они сбивают нормировку гистограммы. Их можно использовать отдельно, как меру масштаба текстуры.
Код:
from PIL import Image
import matplotlib.pyplot as plt
import numpy as np
def compute_direction(x, y, threshold_delta):
return 1 if x - y > threshold_delta else 0
# 7 0 1
# 6 x 2
# 5 4 3
def compute_lbp(data, i, j, threshold_delta):
result = 0
result += compute_direction(data[i, j], data[i-1, j], threshold_delta)
result += 2 * compute_direction(data[i, j], data[i-1, j+1], threshold_delta)
result += 4 * compute_direction(data[i, j], data[i, j+1], threshold_delta)
result += 8 * compute_direction(data[i, j], data[i+1, j+1], threshold_delta)
result += 16 * compute_direction(data[i, j], data[i+1, j], threshold_delta)
result += 32 * compute_direction(data[i, j], data[i+1, j-1], threshold_delta)
result += 64 * compute_direction(data[i, j], data[i, j-1], threshold_delta)
result += 128 * compute_direction(data[i, j], data[i-1, j-1], threshold_delta)
return result
image = Image.open("test.png", "r")
image = image.convert('L') #makes it grayscale
data = np.asarray(image.getdata(), dtype=np.float64).reshape((image.size[1], image.size[0]))
lbps_histdata = []
mean_delta = 0
for i in range(1, image.size[1]-1):
for j in range(1, image.size[0]-1):
mean_delta += (abs(data[i, j] - data[i, j-1]) + abs(data[i, j] - data[i-1, j-1]) +
abs(data[i, j] - data[i-1, j]) + abs(data[i, j] - data[i-1, j+1]) )/4.0
mean_delta /= (image.size[1]-2) * (image.size[0]-2) #normalizing
mean_delta *= 1.5 #we are interested in distinct luminosity changes so let's rise up threshold
for i in range(0, image.size[1]):
for j in range(0, image.size[0]):
if i != 0 and j != 0 and i != image.size[1]-1 and j != image.size[0]-1:
tmp = compute_lbp(data, i, j, mean_delta)
if tmp != 0:
lbps_histdata.append(tmp)
hist, bins = np.histogram(lbps_histdata, bins=254, normed=True)
width = bins[1] - bins[0]
center = (bins[:-1] + bins[1:]) / 2
plt.bar(center, hist, align='center', width=width)
plt.show()
Примеры текстур и результаты:
Больше пикселей
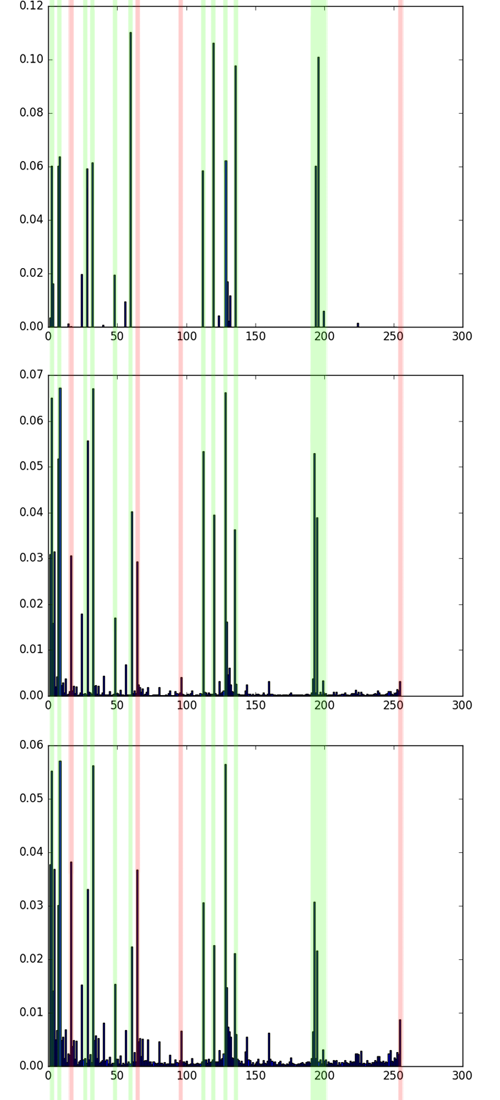
Сравнение гистограмм 4 и 5 картинки, затем сравнение гистограмм 1 и 4 картинки. Зелёным отмечены совпадения, жёлтым — различия. Хотя на этих картинках разные текстуры, 4 и 5 однозначно более похожи, чем 1 и 4. Это видно как на глаз, так и из сравнения гистограмм.
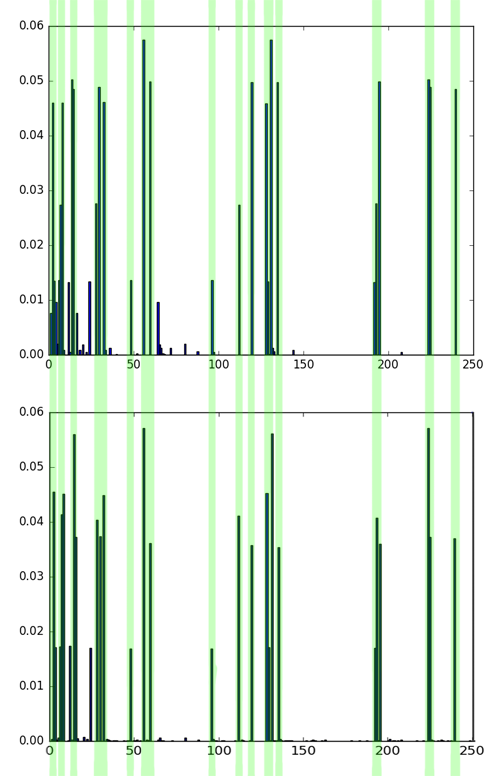
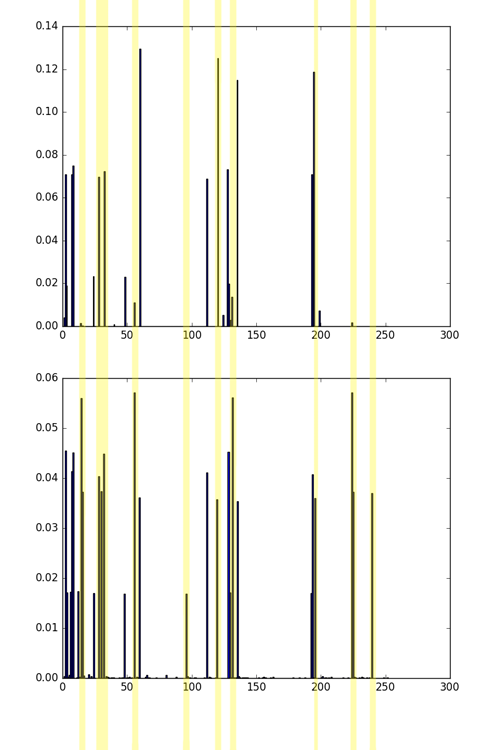
Заметьте, что наибольшие значения зачастую имеют одни и те же бины — они соответствуют униформным паттернам, обсуждавшимся выше. Однако распределение по ним для разных текстур разное. Чем выше уровень шума и хаотичность текстуры, тем больше «мусорных» LBP (см. малочисленные бины на гистограммах).
Список источников
- Dong-Chen He, L. N. (1989). Texture Unit, Texture Spectrum, And Texture Analysis. Geoscience and Remote Sensing Symposium.
- Guoying Zhao, M. P. (2007). Dynamic Texture Recognition Using Local Binary Patterns with an Application to Facial Expressions. IEEE Transactions on Pattern Analysis and Machine Intelligence.
- Hongda Tian, W. L. (2011). Smoke Detection in Videos Using Non-Redundant Local Binary Pattern-Based Features. Wollongong, Australia: Advanced Multimedia Research Lab, ICT Research Institute.
- Jinwang Feng, Y. D. (2015). Dominant–Completed Local Binary Pattern for Texture Classification. Materials of International Conference on Information and Automation. Lijiang, China.
- Junding Sun, G. F. (2013). New Local Edge Binary Patterns For Image Retrieval.
- S. Liao, M. W. (May 2009). Dominant Local Binary Patterns for Texture Classification. Transactions on Image Processing, Vol 18, No 5 .
- T. Ojala, M. P. (1994). Performance evaluation of texture measures with classification based on Kullback discrimination of distributions. Vol. 1 — Proceedings of the 12th IAPR International Conference on Computer Vision & Image Processing .
- Timo Ojala, M. P. (Июль 2002). Multiresolution Gray Scale and Rotation Invariant Texture Classification. IEEE Transactions on Pattern Analysis and Machine Intelligence, 971–987.
- Xiaofeng Fu, R. W. (2012). Spatiotemporal Local Orientational Binary Patterns for Facial Expression Recognition from Video Sequences. International Conference on Fuzzy Systems and Knowledge Discovery.
- Xie Liping, W. H. (July 2014). Video-based Facial Expression Recognition Using Histogram Sequence of Local Gabor Binary Patterns from Three Orthogonal Planes. Proceedings of the 33rd Chinese Control Conference. Nanjing, China.
- Yiu-ming Cheung, J. D. (2014). Ultra Local Binary Pattern For Image Texture Analysis. Materials of IEEE International Conference on Security, Pattern Analysis, and Cybernetics. Wuhan, Hibei, China.
