Обработка больших и очень больших графов11.08.2023 09:47

TLDR

Статья является вводной из цикла статей, посвященных обработке больших и очень больших графов. Приведен обзор основных фреймворков для обработки графов: Pregel, GraphLab и PowerGraph. Описываются способы разбиения графов на части для параллельной обработки. Вводится определение power-law графа (т.е. большинство вершин графа соединены с одной или несколькими вершинами), которых в реальном мире большинство, а так же какие проблемы возникают при обработке таких графов. В заключении приведены доводы для выбора Apache Spark в качестве платформы для обработки.

Мотивация

Однажды ко мне обратилась одна крупная фруктовая телефонная компания с просьбой подготовить для них курс по Apache Spark продвинутого уровня, и в нем обязательно должен быть раздел про обработку графов (Neo4j не предлагать). На тот момент я знал про классические алгоритмы обработки графов на базе DFS (поиск в глубину) и BFS (поиск в ширину). При этом неотъемлемым условием применения того или иного подхода является локальная поддержка стека (DFS) или очереди (BFS). Следовательно, классические алгоритмы можно применять для обработки графов, которые умещаются в память одной машины.

В современном мире данные накапливаются очень быстро, и классические подходы, ориентированные на обработку графов в рамках одной машины, перестают работать, а значит высока потребность в алгоритмах распределенной обработки графов. Интуитивно можно предположить, что необходимо разбивать граф на части, но каким образом и как потом их собирать вместе?

Я знал, что Apache Spark имеет мертвый GraphX и полуготовый GraphFrames. Мне стало интересно разобраться в том, каким образом выполняется обработка огромных графов. Оказалось, что за последние 15 лет разработано несколько алгоритмов распределенной обработки графов, причем каждый подход оформлен в виде публикации в научном журнале. Я поставил себе цель разобраться в этих алгоритмах, и, следуя концепции zero-dependency, перенести их в Apache Spark. Планируемый цикл статей является отражением моих изысканий.

Обработка больших графов

Общее определение

Граф G(V, E, D) представляет собой тройку:

• V — множество вершин,

• E — множество ребер,

• D — множество хранимых данных в ребрах и в вершинах.

Граф не всегда имеет ассоциированные с ним данные. Графы с данными называются Data Graph.

Особенности обработки

При обработке больших графов необходимо принять во внимание следующие моменты:

1. метод разбиения:

   • разбиение по ребрам — вершины равномерно распределены между подграфами,

   • разбиение по вершинам — ребра равномерно распределены между подграфами.

2. программная модель:

   • подграф-центричная (subgraph-centric, SC) — центром внимания является подграф, поэтому можно использовать привычные алгоритмы, но учетом синхронизации промежуточных результатов между подграфами;

   • вершинно-центричная (vertex-centric, VC) — центром внимания является вершина, а алгоритмы составляются из доступных вершине данных: рёбра, веса, значения вершины и т.д…

3. модель исполнения. Процесс вычисления результата на графах является итеративным, поэтому нужно определять когда запускать следующую итерацию. Существует две модели:

   • синхронная — следующая итерация запускается после того, как алгоритм выполнился для подграфов,

   • асинхронная — следующая итерация для подграфа может запуститься вне зависимости от того завершился ли алгоритм на всех подграфах.

4. синхронизация. После выполнения алгоритма на подграфах, необходимо распространить информацию о результате. Это можно сделать двумя способами:

   • разделяемая память,

   • обмен сообщениями.

Разбиение графов

Все методы разбиения графов можно свести к двум способам:

• разбиение по ребрам (edge-cut) — одна вершина может быть только в одном подграфе, ребра могут дублироваться в разных подграфах,

• разбиение по вершинам (vertex-cut) — одно ребро может быть только в одном подграфе, вершины могут дублироваться в разных подграфах.

Разбиение по ребрам

Для разбиения графа по ребрам необходимо разрезать часть рёбер, так чтобы граф развалился на подграфы. Но просто так разрезать ребро нельзя, т.к. потеряется информация об этом ребре. Одно разрезанное ребро фактически заменяется на 2 ребра: одно ребро в одном подграфе, второе ребро в другом подграфе. В подграфах разрезанное ребро заканчивается «фантомной» вершиной, чтобы сохранить информацию о том, куда это ребро ведет. «Фантомные» вершины не участвуют в вычислениях, их цель — поддерживать информацию о «разрезанном» ребре, т.к. ребро не может висеть в воздухе.

На рисунке ниже граф разрезан по ребру между вершинами 3 и 4. После разреза:

• вершина 4 стала фантомной в левом подграфе,

• вершина 3 стала фантомной в правом подграфе,

• ребро между вершинами 3 и 4 присутствует в обоих подграфах.

Разбиение по рёбрам (edge-cut)

Разбиение по вершинам

Граф можно также разрезать по вершинам, фактически разрезаемая вершина дублируется в нескольких подграфах и может участвовать в вычислениях без ограничений.

На рисунке ниже граф разрезан по вершине 3:

• вершина 3 присутствует в обоих подграфах,

• количество ребер в подграфах примерно одинаковое.

Разбиение по вершинам (vertex-cut)

Программная модель

Подграф-центричная программная модель

После разбиения графа на части, каждую часть можно считать отдельным графом — подграфом. Если разбиение выполнялось по вершинам, то в подграфах могут встречаться дубликаты вершин, которые называются «внешними» или «граничными» (frontier). Если разбиение выполнялось по ребрам, то в графах могут встречаться дубликаты ребер, которые также называются «внешними» или «граничными» (frontier).

К каждому подграфу можно применять стандартные алгоритмы обработки графов на базе DFS и BFS. После завершения работы алгоритма, необходимо синхронизировать результаты всех подграфов. Для этих целей используются «граничные» ребра или вершины.

Вершинно-центричная программная модель

В противовес подграф-центричной модели, вершинно-центричная модель требует от программиста разработки новых алгоритмов обработки графов. Особенностью этой программной модели является тот факт, что все программы строятся по принципу »думай как вершина» (think like a vertex).

Принцип »думай как вершина» предписывает программисту использовать только те данные, которые напрямую доступны вершине:

• значение вершины,

• ребра входящие и исходящие,

• веса ребер.

Разработанный алгоритм отправляется на каждую вершину и обработка вершин выполняется параллельно.

Модель исполнения

Вычисление результата на графах обычно включает в себя четыре стадии:

1. запуск алгоритма на всех вершинах или подграфах одновременно,

2. сбор результатов,

3. синхронизация результатов,

4. обновление состояния (данных в графе).

В зависимости от выбранной модели исполнения возможны различные эффекты.

Синхронная модель

При синхронной модели исполнения каждая стадия выполняется строго после предыдущей. К плюсам такого подхода можно отнести отсутствие проблем с гонкой данных, а так же частой необходимостью блокировок. Недостатком может стать неэффективное использование ресурсов кластера.

Например, одна вершина имеет сто ребер, а другая одно ребро. Алгоритм на второй вершине выполнится быстрее, чем на первой, и планировщик будет ждать, пока программа на первой вершине завершит свою работу. Такие проблемы связаны с неравномерным распределением данных. Способы борьбы с обозначенной проблемой описывается ниже в разделе power-law графы.

Асинхронная модель

Асинхронная модель позволяет запускать любую стадию для каждого подграфа или вершины независимо от остальных подграфов и вершин. Такой подход позволяет более эффективно использовать ресурсы, но остро встает вопрос консистентности данных. Программист может выбрать один из уровней консистентности:

• полная консистентность — программы не могут одновременно запускаться на вершинах, которым доступна третья вершина через одно из их ребер. Например, для графа A -> B -> C максимально можно запустить только одну программу на одной из вершин,

• консистентность на уровне ребер — программы не могут одновременно запускаться на вершинах, связанных одним ребром. Например, для графа A -> B -> C максимально можно запустить две программы одновременно: на A и C,

• консистентность на уровне вершин — программы не могут одновременно запускаться на одной и той же вершине. Например, для графа A -> B -> C максимально можно запустить три программы одновременно. Этот уровень уязвим к гонкам данных и требует особого внимания от программиста.

При асинхронной программной модели эффективность алгоритма планировщика в определении вершин, на которых можно запустить программы одновременно, играет ключевую роль.

Итеративность

Указанная выше последовательность стадий называется шагом (superstep). Процесс вычисления результата, обычно, состоит из нескольких шагов, и на каждом шаге итоговый результат уточняется. Таким образом, проявляется итеративная природа вычислений на графах: необходимо выполнить один и тот же алгоритм несколько раз, чтобы получить конечный результат.

Синхронизация

После запуска алгоритма на подграфах, необходимо собрать результаты со всех подграфов для финальной агрегации.

Синхронизация через разделяемую память

Каждый процесс может обновить информацию в объекте, который доступен всем остальным процессам. Необходимо блокировать разделяемый объект, чтобы исключить гонку данных. Тут заявляют о себе законы Амдала (Wikipedia) при оценке задержки (latency) и Густавсона (Wikipedia) при оценке пропускной способности (throughput). Эффективные алгоритмы блокировки и сокращение времени в критических секциях являются ключом к быстродействию системы.

Синхронизация через обмен сообщений

Обмен сообщений позволяет исключить необходимость блокировок и достичь асинхронного взаимодействия, но в то же время остро встает вопрос о гарантиях доставки сообщений и ее надежности.

Power-law графы

Power-law (Wikipedia) графы — это графы, в которых большинство вершин соединены с небольшим подмножеством вершин. В связи с этим у некоторых вершин очень мало рёбер, а у небольшого числа вершин очень много рёбер. Очень часто на практике встречаются именно такие графы, например:

• у знаменитостей может быть несколько миллионов подписчиков в социальных сетях, тогда как у обывателей их несколько десятков или сотен,

• на популярные сайты ведёт больше всего ссылок.

Пример power-law графа представлен на картинке ниже:

• на вершину 3 ссылаются все остальные вершины,

• по одному входящему ребру еще имеют вершины 2 и 4,

• вершины 1, 4, 5 и 6 не имеют входящих ребер.

Пример power-law графа

Таким образом, если применять механизм разбиения графов по ребрам, где одна вершина может находиться только в одном подграфе, то подграфы с вершинами высокой степени (число рёбер) будут обрабатываться на много дольше, чем подграфы, в которых нет таких вершин. Поэтому наиболее удачным решением для power-law графов будет разбиение по вершинам, чтобы количество рёбер было равномерно распределено между подграфами.

Обзор фреймворков

Основные фреймворки для обработки больших и очень больших графов:

Среди приведенных фреймворков будут рассмотрены три:

• Pregel,

• GraphLab,

• PowerGraph.

Фреймворки Pregel и Graphlab были пионерами в области обработки больших и очень больших графах. Остальные фреймворки так или иначе развивают их идеи. Фреймворк PowerGraph первым предложил решение проблем с обработкой power-law графов через разбиение графа по вершинам. Далее будет проведен обзор этих трех фреймворков.

Фреймворк Pregel

Специалисты компании Google одни из первых столкнулись с проблемой обработки больших графов, и поэтому разработали фреймворк Pregel для решения этих задач. Публикация идей, лежащих в основе Pregel, привела к созданию открытого проекта Apache Giraph.

Программная модель отдаленно напоминает map-reduce: разработчик пишет алгоритм, который рассылается каждой вершине в графе. Процесс вычисления итогового результата выглядит следующим образом:

1. каждая вершина при помощи общего алгоритма может сформировать сообщение и отправить его соседям, которые находятся на другой стороне исходящего из вершины ребра;

2. все сообщения складываются в почтовый ящик каждой вершины (количество почтовых ящиков равно количеству вершин);

3. каждая вершина берет информацию из своего почтового ящика и при помощи указанного алгоритма формирует новое сообщение, которое отправляет соседям.

Цепочка действий выше называется superstep (шаг). Для достижения итогового результата необходимо запустить алгоритм несколько раз. Конечный результат можно получить при достижении одного из двух условий:

• определенное количество шагов (superstep) выполнилось,

• ни у одной вершины нет новых сообщений.

На любом шаге вершина может деактивировать себя, чтобы сообщить планировщику, что она не будет участвовать в расчетах на следующем шаге (superstep), но планировщик активирует ее принудительно, если для нее поступят новые сообщения.

Также программист может определить ассоциативную ((a + b) + c = a + (b + c)) и коммутативную (a + b = b + a) операцию для слияния множества сообщений в одно для сокращения трафика при передаче сообщений.

Примечание: Pregel — это название реки в городе Кёнигсберг (современный Калининград), над которой были воздвигнуты семь мостов. Леонард Эйлер поставил себе задачу определить есть ли способ пройти по всем мостам, не проходя ни по одному из них дважды (Wikipedia). Решение этой задачи считается первым в истории применением теории графов.

Программный интерфейс Pregel

Идеи распределенных алгоритмов на графах на Pregel будут демонстрироваться на базе следующего API:

class PregelVertex(Protocol[VertexValue, EdgeValue, MessageValue]):

    @abstractmethod
    def compute(self, messages: List[MessageValue]) -> None:
        ...

    @abstractmethod
    def send_message(self, target_vertex_id, message: MessageValue):
        ...

    @abstractmethod
    @property
    def value(self) -> VertexValue:
        ...

    @abstractmethod
    @value.setter
    def value(self, new_value: VertexValue) -> None:
        ...

    @abstractmethod
    def out_edges(self) -> List[EdgeValue]:
        ...

Комментарии к коду:

• PregelVertex представляет собой абстракцию над вершиной графа, которая имеет три типовых параметра:

  1. VertexValue тип данных, которые могут храниться в вершине,

  2. EdgeValue тип данных для абстракции над ребрами;

  3. MessageValue тип данных передаваемых сообщений.

• метод compute принимает на вход список сообщений и вычисляет новое значение, которое сохраняется внутри текущего объекта,

• метод send_message отправляет сообщение указанной вершине,

• метод value представляет собой property для доступа к текущему значению,

• метод out_edges позволяет получить список исходящих из текущей вершины ребер.

Оригинальная публикация допускает отправку сообщений произвольным вершинам. Концептуально, если отправлять сообщения несуществующим вершинам, то можно создавать новые вершины. На практике список адресатов составляют только из списка непосредственных соседей. Такое ограничение позволяет применять более эффективные алгоритмы разбиения графов с учетом локальности данных.

Пример «Связные компоненты»

Решение задачи поиска связных компонент позволяет разделить граф на подграфы, между которыми нет связей (Wikipedia). Иными словами, необходимо разбить вершины и ребра графа на непересекающиеся множества. В результате каждая вершина должна быть помечена тегом, который позволяет определить ее принадлежность к определенному подграфу.

Алгоритм на Pregel выглядит следующим образом (подробные комментарии ниже):

class CCPregelVertex(PregelVertex[int, Tuple[CCVertex, CCVertex], int]):

    def __init__(self, id: int):
        self.id = id
        self.value = id

    def compute(self, messages: List[int]) -> None:
        min_message_value = min(messages)

        if self.value > min_message_value:
            self.value = min_message_value

            for _, target in self.out_edges():
                self.send_message(target.id, self.value)
        

Комментарии к коду:

• CCPregelVertex наследует PregelVertex, где типовые параметры:

  1. int — тип значения, т.е. номер компонента связности/подграфа, к которому относится текущая вершина;

  2. Tuple[CCVertex, CCVertex] — тип ребра в формате: (исходная вершина, конечная вершина);

  3. int — тип сообщения, т.е. номер подграфа, в котором должны жить соседние вершины.

• изначально предполагается, что в графе нет ребер, а значит каждая вершина является компонентом связности/подграфом;

• метод compute корректирует номер подграфа, в котором находится текущая вершина:

  1. на вход приходят сообщения, которые были отправлены текущей вершине;

  2. выполняется поиск минимального сообщения;

  3. минимальное сообщение сравнивается с текущим значением — минимальное из двух будет являться номером подграфа, который содержит текущую вершину;

  4. если значение в текущей вершине было обновлено, то оповестить об этом соседей.

• реализация остальных методов исключена, т.к. по большей части зависит от окружения.

Вопрос на понимание: Какая логическая ошибка есть в реализации?

Процесс вычисления конечного результата является итеративным (планировщик выполняет superstep много раз), и программист сам должен управлять сходимостью алгоритма и прервать его, когда полученный результат будет устраивать. В худшем случае (когда граф — это связный список без циклов) количество необходимых шагов (superstep) будет линейно зависеть от диаметра самой большой связной компоненты.

В графе ниже существует две связные компоненты: 1 и 6

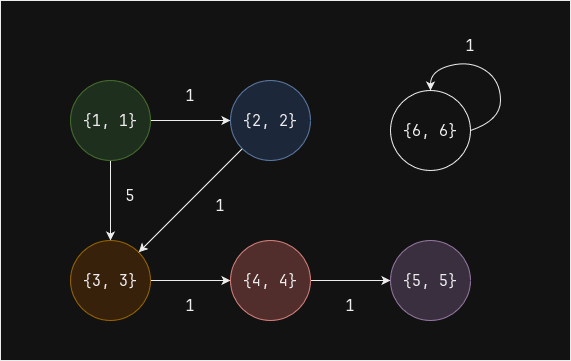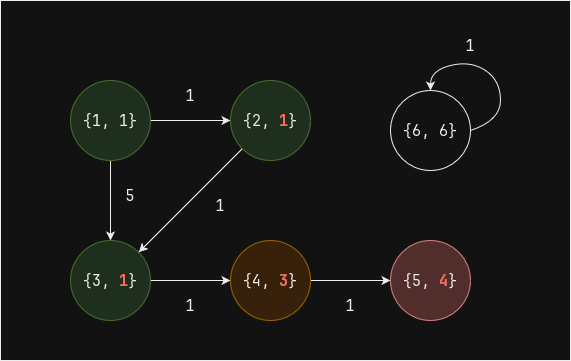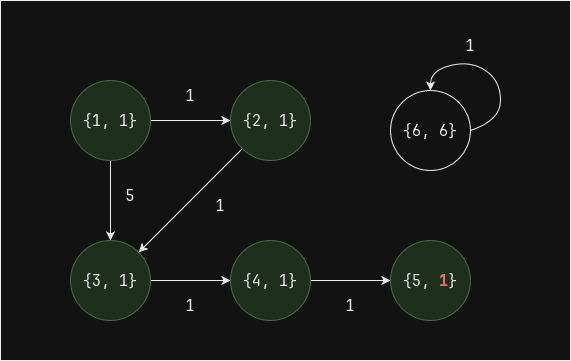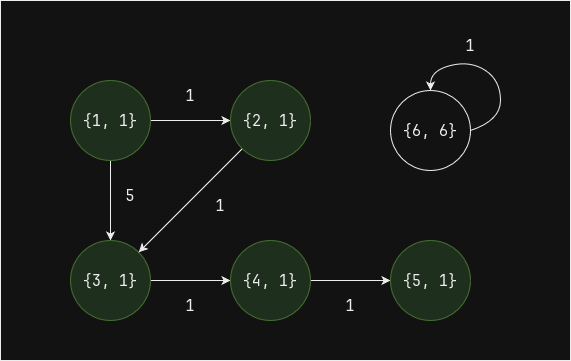
Итеративное вычисление связных компонент

Больше примеров будет разобрано в следующей статье цикла.

Фреймворк GraphLab

Независимо от Pregel в университете Карнеги — Меллона был разработан фреймворк для параллельной обработки графов GraphLab. Он представляет собой асинхронный фреймворк для обработки больших графов при помощи разделяемой памятью. Подобно Pregel основой фреймворка является вершинно-центричная программная модель, а программы реализуются благодаря идиоме «думай как вершина». Программа может обращаться к:

• данным текущей вершины,

• весам входящих и исходящих рёбер,

• данным смежных вершин независимо от направления ребра.

Разработанный программистом алгоритм оправляется на все вершины графа. Асинхронный подход позволяет быстро обрабатывать вершины с небольшим числом рёбер и не зависеть от медленной обработки вершин с большим числом рёбер. К минусам можно отнести повышенную потребность в блокировках.

Обрабатываемый граф не может мутировать в процессе обработки.

Программный интерфейс GraphLab

class GraphLabVertex(Protocol[VertexValue, EdgeValue]):

    @dataclass
    class Scope(Generic[EdgeValue]):
        inward_edges: List[EdgeValue]
        outward_edges: List[EdgeValue]

    @abstractmethod
    def update(self, scope: 'GraphLabVertex.Scope'):
        ...

    @abstractmethod
    @property
    def value(self) -> VertexValue:
        ...

    @abstractmethod
    @value.setter
    def value(self, new_value: VertexValue) -> None:
        ...

Комментарии к коду:

• GraphLabVertex представляет собой абстракцию над вершиной графа, которая имеет два типовых параметра:

  1. VertexValue тип данных, которые могут храниться в вершине,

  2. EdgeValue тип данных для абстракции над ребрами.

• класс Scope хранит информацию о смежных ребрах и вершинах,

• метод update:

  • принимает на вход scope — окрестность текущей вершины вместе с ребрами и смежными вершинами,

  • вычисляет новое значение, которое сохраняется внутри текущего объекта.

• метод value представляет собой property для доступа к текущему значению.

Отказ от обмена сообщениями ведет к разделению бизнес логики и механизма обновления данных, позволяя системе самостоятельно принимать решение, как и когда изменять состояние программы.

Пример «Связные компоненты»

class CCGraphLabVertex(GraphLabVertex[int, Tuple[CCGraphLabVertex, CCGraphLabVertex]]):

    def __init__(self, id: int):
        self.id = id
        self.value = id

    def update(self, scope: GLVertex.Scope) -> None:
        min_inward_value = min([ inward_vertex.value for inward_vertex, _ in scope.inward_edges ])
        min_outward_value = min([ outward_vertex.value for _, outward_vertex in scope.outward_edges ])
            
        self.value = min(min_inward_value, min_outward_value, self.value)
        

Комментарии к коду:

• CCGraphLabVertex наследует GraphLabVertex, где типовые параметры:

  1. int — тип значения, т.е. номер компонента связности/подграфа, к которому относится текущая вершина;

  2. Tuple[CCGraphLabVertex, CCGraphLabVertex] — тип ребра в формате: (исходная вершина, конечная вершина).

• изначально предполагается, что в графе нет ребер, а значит каждая вершина является компонентом связности/подграфом;

• метод update корректирует номер подграфа, в котором находится текущая вершина:

  1. на вход подается scope: набор входящих и исходящих ребер вместе с вершинами;

  2. выполняется поиск минимального значения среди смежных вершин из набора входящих ребер;

  3. выполняется поиск минимального значения среди смежных вершин из набора исходящих ребер;

  4. выбирается минимальное значение между текущим значением и минимальным значением смежных вершин — это значение будет являться номером подграфа, который содержит текущую вершину.

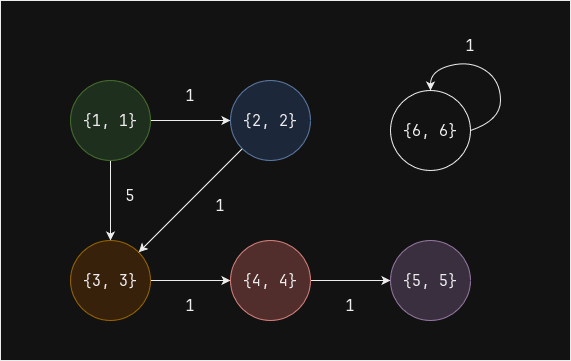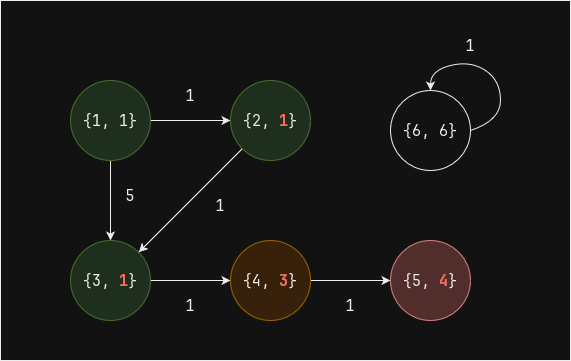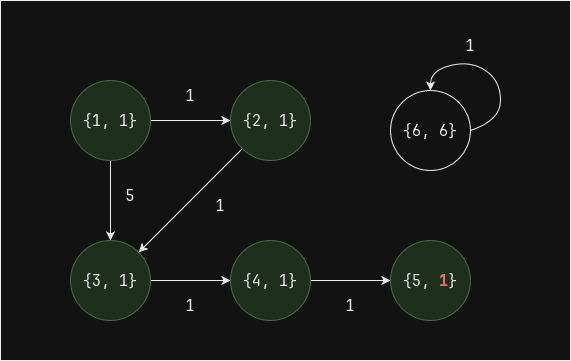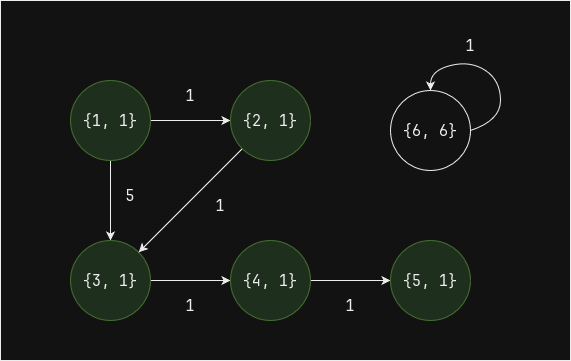
Итеративное вычисление связных компонент

Больше примеров будет разобрано в статье, посвященной GraphLab.

Фреймворк PowerGraph

Фреймворк PowerGraph является развитием идей GraphLab и был создан командой GraphLab, как ответ на проблему power-law графов. Подобно Pregel и Graphlab фреймворк PowerGraph является вершинно-центричным (Vertex-Centric). Фреймворк предлагает синхронную и асинхронную модель исполнения. В отличие от Pregel и GraphLab фреймворк PowerGraph применяет разбиение по вершинам (vertex-cut), что позволяет распределить ребра графа равномерно между подграфами.

PowerGraph диктует GAS модель при разработке программ:

• Gather — собрать информацию со смежных вершин и ребер в виде «обобщенной суммы» (generalized sum),

• sum — коммутативная, ассоциативная операция для слияния всех сумм из предыдущего шага в одно значение,

• Apply — вычислить новое значение текущей вершины на базе текущего значение и результирующей суммы,

• Scatter — вычислить новое значение рёбер.

Программный интерфейс GraphLab

class PowerGraphVertex(Protocol[VertexValue, EdgeValue, Accum]):

    @abstractmethod
    def gather(self, data_uv: EdgeValue, data_v: VertexValue) -> Accum:
        ...

    @staticmethod
    def sum(left: Accum, right: Accum) -> Accum:
        ...

    @abstractmethod
    def apply(self, s: Accum) -> None:
        ...

    @abstractmethod
    def scatter(self, data_uv: EdgeValue, data_v: VertexValue) -> EdgeValue:
        ...

    @abstractmethod
    @property
    def value(self) -> VertexValue:
        ...

    @abstractmethod
    @value.setter
    def value(self, new_value: VertexValue) -> None:
        ...

Комментарии к коду:

• PowerGraphVertex представляет собой абстракцию над вершиной графа, которая имеет три типовых параметра:

  1. VertexValue тип данных, которые могут храниться в вершине,

  2. EdgeValue тип данных, которые могут храниться в ребре,

  3. Accum тип данных для аккумулятора.

• метод gather принимает значение ребра и смежной вершины и возвращает значение аккумулятора. Параметры метода:

  1. data_uv — значение ребра из текущей вершины до смежной вершины,

  2. data_v — значение смежной вершины.

• метод sum позволяет «сложить» два аккумулятора и получить новое значение аккумулятора. PowerGraph разрезает вершины, значит одна вершина может находиться в нескольких подграфах, поэтому необходим способ синхронизации значений между ними;

• метод apply принимает значение результирующего аккумулятора и вычисляет новое значение текущей вершины;

• метод scatter принимает значени ребра и смежной вершины и вычисляет новое значение ребра;

• метод value представляет собой property для доступа к текущему значению.

Пример «Связные компоненты»

class CCPowerGraphVertex(PowerGraphVertex[int, None, int]):

    def __init__(self, id: int):
        self.id = id
        self.value = id

    def gather(self, data_uv: None, data_v: int) -> int:
        return data_v

    @staticmethod
    def sum(left: int, right: int) -> int:
        return min(left, right)

    def apply(self, sum_acc: int) -> None:
        self.value = min(self.value, sum_acc)

    def scatter(self, data_uv: None, data_v: int) -> None:
        return None

Комментарии к коду:

• CCPowerGraphVertex наследует PowerGraphVertex, где типовые параметры:

  1. int — тип значения вершины, т.е. номер компонента связности/подграфа, к которому относится текущая вершина;

  2. None — тип значения ребра, в алгоритме значения ребер не используются, поэтому None;

  3. int — тип значения аккумулятора;

• изначально предполагается, что в графе нет ребер, а значит каждая вершина является компонентом связности/подграфом;

• метод gather возвращает значение смежной вершины в качестве аккумулятора;

• статический метод sum позволяет вычислить минимальное значение между всеми аккумуляторами, т.е. минимальное значение всех смежных вершин;

• метод apply принимает самое минимальное значение всех смежных вершин устанавливает его значением текущей вершины, если оно меньше текущего значения;

• метод scatter должен обновить значение ребер, но в этом алгоритме значения ребер не используются, поэтому просто возвращается None.

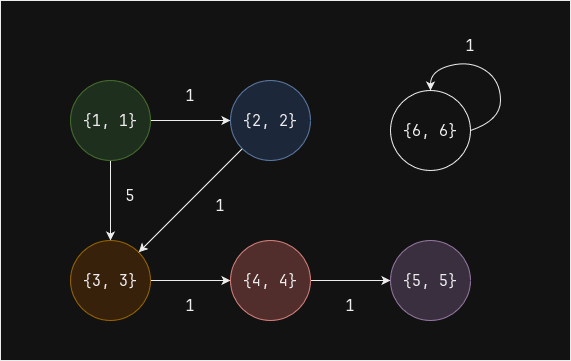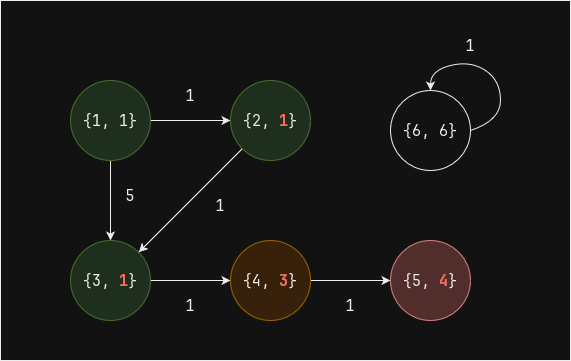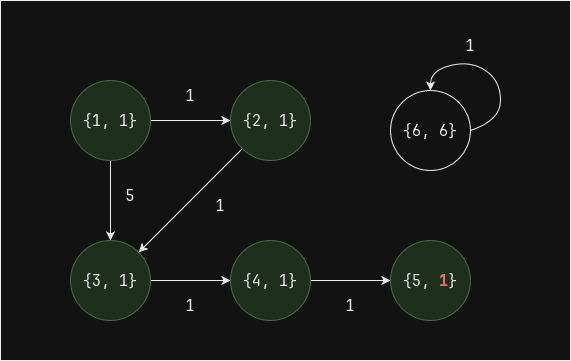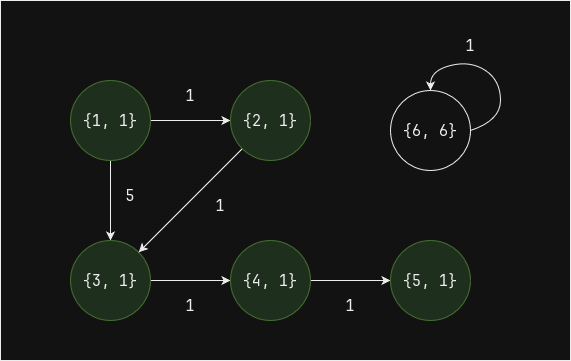
Итеративное вычисление связных компонент

Больше примеров будет разобрано в статье, посвященной PowerGraph.

Apache Spark

Apache Spark является одним из наиболее популярных инструментов для анализа больших данных, поэтому будет логичным реализовать рассмотренные концепции на базе его возможностей. Apache Spark так же выбран благодаря встроенным алгоритмам партиционирования, а алгоритм партиционирования по умолчанию позволит избавиться от проблем, вызываемых power-law графами. Также в нем имеется мощный оптимизатор запросов, который позволит достигать максимальной производительности. Дополнительная оптимизация производительности, обычно включает в себя настройку форматов данных и их расположение.

Итеративность в Apache Spark

Управляющая программа (driver) в Apache Spark строит план запроса, который потом исполняется на воркерах (executors). Так каждая команда, например, фильтрация, преобразование, слияние и т.д., является всего лишь узлом в плане запроса. Благодаря этому факту, новые планы запросов можно строить на базе уже имеющихся планов.

Рассмотрим простой пример эволюции плана запроса:

1. Создать DataFrame из одной строки и одной колонки:

df = spark.sql("select rand() as id")
df.explain()

== Physical Plan ==
*(1) Project [rand(1533802073737075276) AS id#49]
+- *(1) Scan OneRowRelation[]

1. Выполнить фильтрацию — к предыдущему плану добавился новый узел Filter:

df = df.where("id > 0")
df.explain()

== Physical Plan ==
*(1) Filter (id#49 > 0.0)
+- *(1) Project [rand(1533802073737075276) AS id#49]
   +- *(1) Scan OneRowRelation[]

Обратите внимание, что датафрейм, полученный после применения операции фильтра к df, снова сохранятеся в переменной df

1. Изменить значение колонки id — добавился новый узел Project:

df = df.select("id", F.rand())
df.explain()

== Physical Plan ==
*(1) Project [id#49, rand(-6415673197654941820) AS rand(-6415673197654941820)#51]
+- *(1) Filter (id#49 > 0.0)
   +- *(1) Project [rand(1533802073737075276) AS id#49]
      +- *(1) Scan OneRowRelation[]

1. Указанные действия можно выполнять и в цикле:

for _ in range(5):
    df = df.where("id > rand()").select("id", F.rand())

df.explain()

== Physical Plan ==
*(1) Project [id#49, rand(263374480755633512) AS rand(263374480755633512)#159]
+- *(1) Filter (id#49 > rand(8987503485164949684))
   +- *(1) Filter (id#49 > rand(-1547883987418598842))
      +- *(1) Filter (id#49 > rand(-692100532660493196))
         +- *(1) Filter (id#49 > rand(4695896702299530223))
            +- *(1) Filter (id#49 > rand(6199414182906311709))
               +- *(1) Filter (id#49 > 0.0)
                  +- *(1) Project [rand(1533802073737075276) AS id#49]
                     +- *(1) Scan OneRowRelation[]

Возможность генерации плана в цикле будет использоваться для запуска итеративного процесса вычисления результата на графах.

Итоговый план запроса может быть очень большим, что можно отнести к недостаткам такого подхода. Тут стоит учитывать, что план будет иметь «фрактальный рисунок»: малая часть плана будет выглядеть как весь план, что облегчает анализ.

Так же к недостаткам можно отнести тот факт, что управляющая программа (driver) может не справиться с генерацией большого плана по причине нехватки ресурсов. Для решения этой проблемы можно использовать checkpoint: драйвер будет запускать исполнение плана по частям.

Заключение

Эра больших данных требует создания новых алгоритмов. В области обработки графов эта проблема стоит особенно остро, т.к. подавляющее число алгоритмов на графах использует BFS или DFS, которые малоприменимы в распределенных системах. Обработка больших графов может использовать устоявшиеся принципы для обработки больших данных, такие как:

• разбиение целого на части: партиционирование,

• модель исполнения: синхронная, асинхронная,

• синхронизация: разделяемая память, обмен сообщениями.

Но в тот же момент появляются и свои особенности, программисту необходимо принимать решения:

• о программной модели: вершинно-центричная, подграф-центричная,

• о способе разбиения графа: разрезать вершины или рёбра,

• о планировщике в соответствии с уровнем консистентности: полная консистентность, консистентность на уровне рёбер, консистентность на уровне вершины.

Доминирующим способом разбиения графов является разбиение по ребрам, т.е. одна вершина может принадлежать только одному подграфу (или быть фантомной). Разбиение по рёбрам ведёт к перекосам (skew) при распределении данных, когда граф является power-law графом, что снижает эффективность использования ресурсов кластера. Для power-law графов предпочтительным способом разбиения является разбиение по вершинам: одна вершина может присутствовать в нескольких подграфах.

В следующей статье будет рассмотрен фреймворк Pregel и его реализация на базе Apache Spark DataFrame API.

© Habrahabr.ru