О математике и пандемиях
Disclaimer 1Я математик, НЕ ВРАЧ и не являюсь профильным специалистом-эпидемиологом, а свою последнюю научную работу на тему матмоделирования эпидемий написал без малого 20 лет назад. По всем вопросам здоровья, коронавирусов и смысла жизни консультируйтесь с лечащим врачом, не будьте глупыми людьми.
Disclaimer 2Ниже будет некоторое количество графиков. Перед их построением я умышленно декалибровал и упростил модель, отстроившись от параметров COVID-19. Приведенные графики демонстрируют развитие эпидемии некоторого условного вируса в некоторой условной популяции в условном времени. Не делайте предсказаний о ходе текущей пандемии, опираясь на мои картинки, не будьте глупыми людьми.
Ну, а теперь — поехали! По понятным причинам, ныне изрядно подскочил интерес ко всякому пандемическому, и всевозможные математические и не очень математические модели бродят по соцсетям стаями. Число же эпидемиологов и специалистов по системам дифференциальных уравнений и вовсе превысило все мыслимые пределы. Тем не менее, во всем этом информационном буйстве странным образом обойдены молчанием перколяционные, они же стохастические имитационные, модели. Этот недостаток мы сейчас немедленно исправим. Кстати, впервые о подобных моделях (как и многом другом) я прочитал в замечательной книжке Гулда и Тобочника «Компьютерное моделирование в физике».
Устроена перколяционная модель обманчиво просто. Для начала мы создаем общую компьютерную модель индивидуума, участвующего в эпидемии. Что-нибудь не слишком сложное: здоров, болен, выздоровел, умер и условия перехода между состояниями. На основе статистических данных об исследуемой популяции, каждый конкретный экземпляр случайным образом наделяется теми или иными характеристиками, à la возраст, пол (если это важно), крепость иммунитета и т.п. Наделав кучку таких конкретизированных экземпляров, мы размещаем их в вершинах некоторого графа, имитирующего социальные связи. После этого остается задать условия передачи инфекции между индивидуумами, заразить несколько первых счастливчиков и дать старт эпидемии.
Большим преимуществом подобного подхода является простота модификации и свобода от многочисленных априорных допущений, позволяющие быстро прогнать модель для самых разных, даже экзотических сценариев. Примеры мы увидим ниже. Обратной стороной данного метода является то, что строгое математическое описание и анализ возникающих в такой системе эффектов зачастую очень сложен (мягко говоря). Впрочем, поэкспериментировать это нам не помешает.
Довольно болтовни, к делу! Возьмем 16 миллионов пацаков и равномерно разместим на гиперсфере. Соседей соединим в граф каким-нибудь регулярным шаблоном. Это изрядное упрощение для социального графа, но мы, слава богу, не минздрав. Заразу будем распространять каждый день двумя путями. Во-первых, пацак на каждом шаге может с некоторой вероятностью заразиться от больных соседей. Во-вторых, с некоторой другой вероятностью, он может на каждом шаге заразиться от случайного пацака, не входящего в его окружение (эффект «общественного транспорта»). Ну и наконец, сама болезнь. Период бессимптомного носительства примем длиной 10 шагов, после чего пацак показывает симптомы и больше в распространении не участвует. Следующие 10 шагов он болеет, имея на каждом шаге некоторый шанс скопытиться. После этого он выздоравливает (если доживет, конечно). Начальный посев примем 100 пацаков.
При указанных условиях, получаем следующую картинку:

Фиолетовым показан процент незараженных пацаков, желтым — заболевших, зеленым — выздоровевших, черным — сами понимаете.
Посмотрим теперь на больных поближе:

Здесь на каждом шаге красненьким показан процент болеющих, но еще бессимптомных пацаков, а синим — проявляющих симптомы.
Теперь вернемся к первому графику и взглянем попристальней на начальную фазу эпидемии (легенда та же):
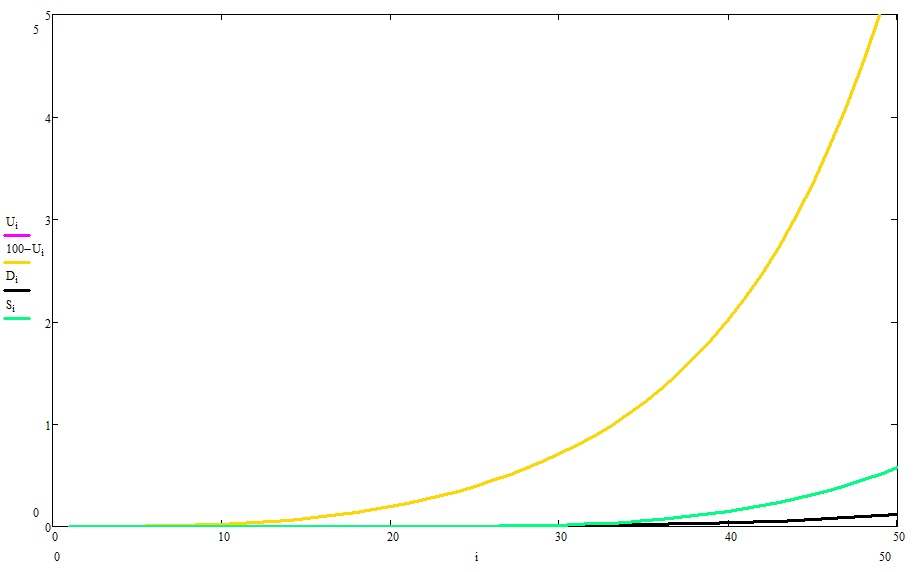
Да-да. Эта та самая экспонента, которой СМИ уже всю плешь проели. Если на пальцах, то происхождение этой самой экспоненты таково: в условиях, когда число носителей мало, а общественная жизнь поставляет носителю новых случайных незараженных пацаков, число новых заражений прямо пропорционально числу носителей. Математически это записывается в виде дифференциального уравнения

решением которого является, вы жеж не поверите, экспонента. Такая штука много где в природе встречается, в частности, одним из ярчайших примеров, во всех смыслах, является неуправляемая цепная реакция. Потом, с ростом числа носителей, хялява для инфекционного агента заканчивается, но в рамках текущей пандемии, например, эта фаза еще не пройдена. Если вышеприведенное уравнение слегка усложнить и подкрутить, для учета исчерпаемости ресурсов для размножения, то мы получим классическое уравнение Ферхюльста (aka логистическое уравнение):
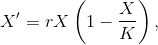
краеугольный камень популяционной динамики. Если вы когда-нибудь слышали о r-стратегиях и K-стратегиях размножения, так вот это в честь коэффициентов из приведенного уравнения названо. Решения логистического уравнения на глаз совершенно неотличимы от графиков с первого рисунка (что не слишком-то удивительно), поэтому я их отдельно приводить не буду. К сожалению, уравнение Ферхюльста для наших задач является чрезмерным упрощением, поэтому мы с ним прощаемся и идем дальше.
Давайте теперь примем меры, скажем, отправим пацаков на выходные и закроем общественный транспорт и мероприятия до конца эпидемии. В рамках модели, это будет означать, что инфекция распространяется теперь только вдоль ребер социального графа, от родственника родственнику, от друга к другу. Ну и да, очевидно, чатлане спохватились не сразу, поэтому меры мы примем, когда заболеет 1000 пацаков.
В том же масштабе времени:
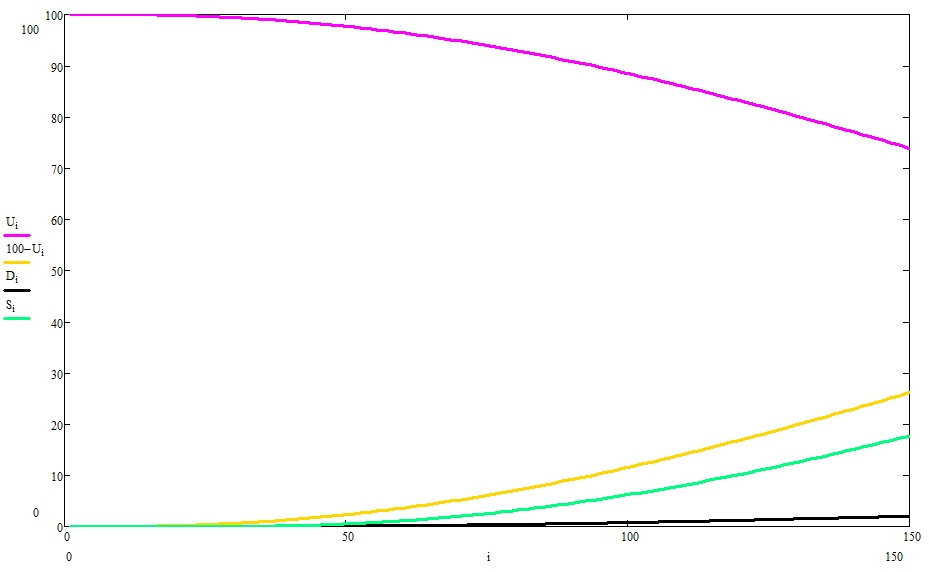
и
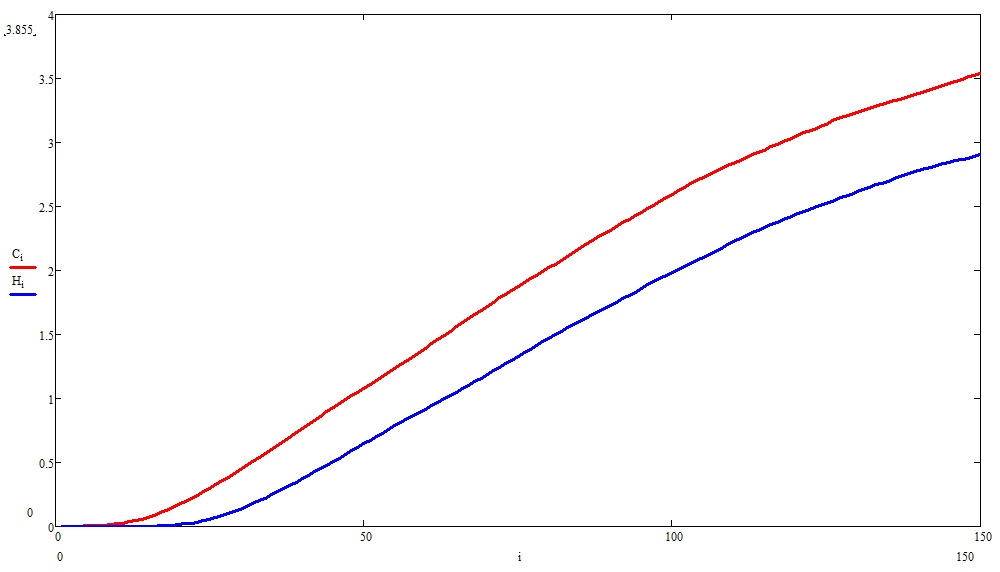
Заметьте, в прошлом эксперименте эпидемия без «ограничительных мер» успела потухнуть, а здесь еще и даже до пика расти и расти.
Взглянем на эпидемию целиком:
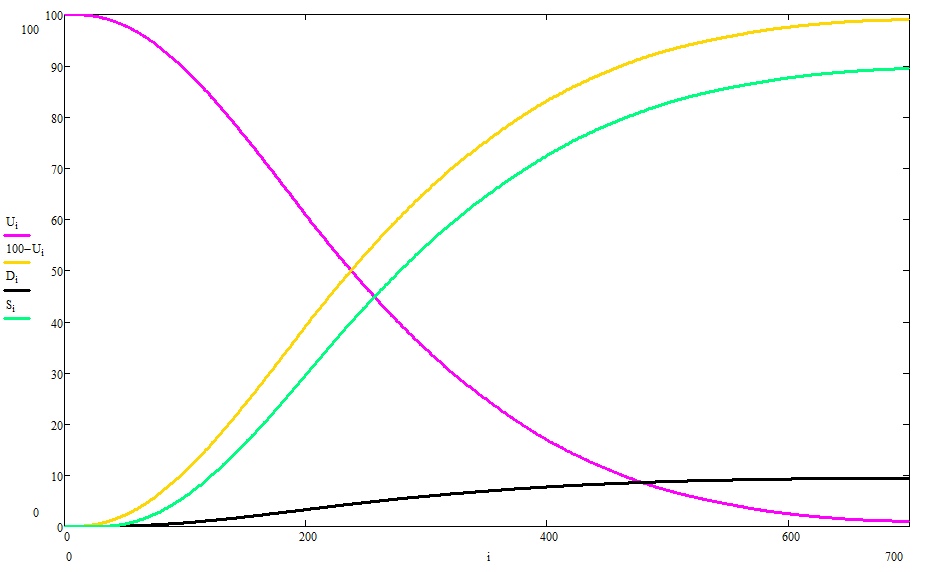
Как видите, время эпидемии растянулось в немалые разы.
Особенно важен пошаговый график:

Принятые меры на порядок снизили количество одновременно болеющих. Почему это важно, будет видно ниже.
Возможно, на графиках не так хорошо заметно, но основной эффект в том, что после принятия мер экспоненциальный рост числа заболевших почти моментально сменяется степенным. Грубо на пальцах, это можно объяснить следующим образом: каждый новый заболевший становится сам источником заразы и начинает заражать всех вокруг (эдакий инфекционный принцип Гюйгенса). Но это «вокруг» ограниченно лишь немногочисленными незараженными соседями, которые заражаясь сами, передают инфекцию дальше. Таким образом, вокруг очага образуется «волновой фронт», который с некоторой постоянной скоростью расползается во все стороны (кто сказал «эйконал» —тот молодец), а число инфицированных —это объем «пространства», заметенный волновым фронтом, который (чистая геометрия) пропорционален некоторой степени пройденной фронтом дистанции.
Ну и последний эксперимент на сегодня. Будем щедры к системе здравоохранения, но при этом добавим реализму. Пусть порог ее насыщения — одномоментно болеющие 10% популяции (это заведомо гораздо круче реальности) и пусть вероятность склеить ласты у пацака, которому не досталось койки, возрастает в 10 раз. Пусть, наконец, чатлане не озаботились каникулами для пацаков (обсчитывать такой сценарий для случая с каникулами смысла нет, у минздрава в указанной постановке в самый пиковый момент останется тройной запас прочности). Тогда получим:

Точка насыщения достигается в районе 75 шага, как раз над буковкой i. Чтоб вы вдруг не подумали, что «минздрав не нужен», вот вам еще графики для случая, когда медицина не то, чтобы перенасытилась, а ее не было изначально (добро пожаловать в средневековье):
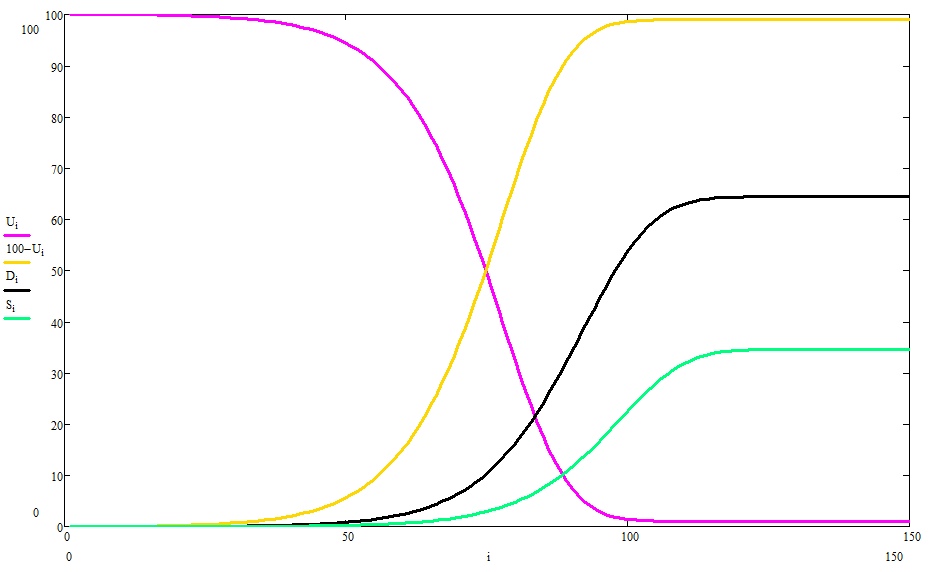
Такие дела. Не болейте!
