Неравенства Белла — физика и математика09.02.2021 04:48

Эта статья — очередная попытка популярно изложить суть неравенства Белла и парадокса Эйнштейна-Подольского-Розена. Статьи, которые мне попадались ранее, либо сходу начинали с физических формул. и содержали кучу бра-кетов, тензорных произведений и прочих эрмитовых операторов. Что не способствовало пониманию среди широкой аудитории (вроде меня). Либо содержали довольно простые математические рассуждения, но непонятно как соотносящиеся с реальными физическими экспериментами. Либо были недостаточно подробными (в стиле «видите 2 линии на графике? Что и требовалось доказать»). Либо вообще неверными! Когда автор берет три независимых квантовых параметра и из-за ошибки в рассуждениях приходит к выводу, что это будет чем-то принципиально отличаться от трёх самых обычных случайных величин-«монеток».

Последнюю статью я сам считал неплохой иллюстрацией ЭПР-парадокса, пока до меня не дошло что в ней ошибка. После чего решил наконец разобраться с «парадоксом» раз и навсегда. Разбираться будем вместе под катом.

Поляризация в классической оптике

Начнём мы с классической (не квантовой) оптики, в которой есть явление поляризации. Суть его в том, что электромагнитная волна (как и любая другая поперечная волна) может иметь ориентацию в пространстве.

После прохождения устройства под названием «поляризатор», свет немного теряет в интенсивности и становится ориентирован относительно оптической оси поляризатора. Если свет пропустить через такой же параллельный поляризатор — ничего не изменится. Если же один из поляризаторов развернуть на 90° — света на выходе не будет. В общем случае интенсивность света пропорциональна cos2θ, где θ — угол между осями поляризаторов.

Пучок света можно разделить на два с противоположными поляризациями (отличающимися на 90°), например используя закон Брюстера, благодаря которому работают поляризационные фильтры для фотографии. Если поставить поляризаторы на выходе этих пучков общая интенсивность света будет пропорциональна cos2(θ+90°) = sin2θ

Более хитроумным способом разделить пучок являются нелинейные оптические материалы, например бета-борат бария. Большая часть света проходит сквозь него без изменений (и далее нас не интересует), но небольшая часть расщепляется на 2 пучка. Причём при расщеплении соблюдаются законы сохранения энергии и импульса:

Я задержался так подробно на классической оптике, чтобы подчеркнуть, что все что мы будем далее рассматривать не противоречит ее законам и прекрасно наблюдается на макро-уровне.

Квантовый уровень

Во времена становления квантовой механики, физики продемонстрировали беспрецедентный уровень отрицания законов и принципов, которые вроде как давно устоялись. Особенно в отношении природы света:

• свет по-видимому состоит из частиц (Ньютон, 1670-е)

• свет никак не может состоять из частиц (Юнг, 1800-е)

• свет все-таки состоит из частиц (Бор et al, 1910-е)

Ну и куда ж без него:

• Вы там совсем с ума посходили? (Эйнштейн, 1920-е)

Возвращение к корпускулярной теории света (на новом уровне) принесло массу неприятностей с дифракцией и прочим. Рассмотрим конкретно неприятности, касающиеся поляризации.

Если фотон — это неделимая частица, то поляризатор не может пропускать, скажем, половинки фотонов, подобно тому как в классике он пропускал половину волны. Каждый фотон либо проходит полностью, либо не проходит вообще. Поэтому уменьшение интенсивности света вдвое должно означать, что проходит только половина фотонов, причём случайно — прошедшие фотоны ничем не отличаются от поглотившихся.

Возвращаемся к нелинейному бета-борату бария. На квантовом уровне расщепление луча обозначает, что каждый фотон превращается в два. Как я уже говорил, здесь действуют законы сохранения энергии (новые фотоны имеют половинную частоту/энергию) и импульса (они разлетаются под одинаковым углом в разные стороны). Поляризация в микромире соответствует спину, он же момент импульса, с соответствующим законом сохранения. И можно предположить, что у двух пучков будет строго противоположная поляризация, но на практике этого не происходит. Какая-то поляризация у них есть, но совсем не такая строгая.

А в некоторых случаях поляризация отсутствует вообще (светло-зелёные линии на рисунке выше)! Именно этот случай нас и интересует больше всего. Каждый такой фотон может пройти через любой поляризатор с вероятностью ½. Погодите, но если мы поставим оба поляризатора вертикально, то оба фотона по статистике рано или поздно пройдут сквозь них и закон сохранения момента импульса нарушится?

А вот и нет. Потому что оба фотона никогда не проходят через параллельные поляризаторы. Все выглядит так будто фотоны не имеют поляризации (до измерения) и одновременно имеют противоположную поляризацию (после него). Результаты двух измерений случайны, но скоррелированы между собой. Оба поляризатора пропускают примерно каждый второй фотон, но никогда не пропускают их одновременно. Именно такие фотоны называются «запутанными» (entangled). 

Запутанные фотоны

Возникает вопрос «как это работает?».»100% квантовое» объяснение в копенгагенской интерпретации выглядит следующим образом. Два запутанных фотона, левый и правый, имеют общую волновую функцию, описывающую их поведение. Когда левый фотон проходит левый поляризатор, происходит процесс измерения, в котором:

• поляризация фотона выбирается случайным образом

• происходит коллапс волновой функции, «отсекающий» от неё все что противоречит выбранной поляризации

• в частности, поляризация правого фотона становится противоположной левому.

Это значит, что вероятность прохождения правого фотона становится sin2θ (работает классическая формула для противоположной поляризации)

А вероятность прохождения обоих фотонов, следовательно, равна по теории вероятностей:

p (L & R) = p (L) * p (R/L) = ½ * sin2θ

Формула выше прекрасно подтверждается статистическими экспериментами, некоторые из которых мы рассмотрим ниже.

Теория скрытых параметров

Проблема в том, что квантовое объяснение поляризации требует от нас принятия нескольких неочевидных фактов:

• законы природы фундаментально случайны. Мы не можем точно предсказать поведение системы даже если полностью знаем ее состояние

• запутанные фотоны влияют друг на друга мгновенно (или, как минимум, сильно быстрее скорости света), даже если они находятся на разных концах вселенной

Может быть есть более простое объяснение? Допустим что измерение не привносит никаких случайностей. А какие фотоны проходят через какие поляризаторы определяется заранее, при их создании. Прошедший фотон и поглощённый фотон на самом деле отличаются друг от друга, но мы просто не знаем этих деталей, пока не измерим. В конце концов, верхняя карта в перетасованной колоде тоже выглядит для нас «случайной», однако фундаментально это не так. И вообще, разве можно отличить ситуацию «значение параметра нам неизвестно» от «значение параметра в принципе не существует»? Оказывается можно и вот каким способом.

Проведём 3 статистических эксперимента со спутанными фотонами, пропуская их через 2 поляризатора, меняя их углы и считая сколько раз оба фотона прошли насквозь — назовём это «положительным исходом». Эксперименты повторяются много раз для набора статистики. Мы увидим, что результаты в точности соответствуют формуле выше. На практике используются двухканальные поляризаторы, которые не поглощают «неправильные» фотоны, а направляют их на другой детектор,»-1». В любом случае, нас интересует только случаи когда оба фотона пошли по пути »+1».

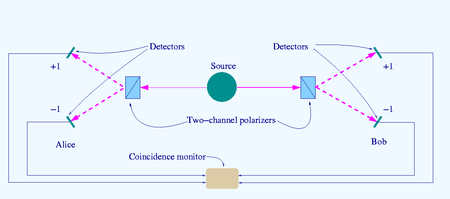
Эксперимент 0 (для разминки)

Пусть оба поляризатора установлены вертикально
Левый угол = 0°
Правый угол = 0°
θ = 0°
р = ½ * sin2θ = 0

Оба фотона никогда не приходят на »+1» одновременно — нет положительных исходов

Эксперимент 1

Отклоняем левый поляризатор на 10° влево (допустим «влево» это отрицательный угол):
Левый угол = -10°
Правый угол = 0°
θ = 10°
p = 1,5%

1,5% положительных исходов

Эксперимент 2

Отклоняем правый поляризатор на 10° вправо (левый возвращаем на место):

Левый угол = 0°
Правый угол = 10°
θ = 10°
p = 1,5%

Тот же результат

Эксперимент 3

Отклоняем оба одновременно:
Левый угол = -10°
Правый угол = 10°
θ = 20°
p = 5,8%

Интуитивно уже кажется, что что-то не так. Как если бы у нас были 3 монетки (с надписями -10°, 0° и 10°). Монетки -10° и 0° одновременно выпадают орлом в 1,5% случаев. Монетки 0° и 10° — тоже. Но монетки -10° и 10° умудряются выпадать гораздо чаще чем в 3% случаев. На интуицию мы полагаться не будем, а посмотрим на строгое доказательство, которое как раз и предложил Белл в своей теореме.

Неравенство Белла

У него есть несколько эквивалентных формулировок. Оригинальная формулировка Белла сразу даёт формулу для спутанных фотонов. Но мы рассмотрим вариант, который математически доказывается проще всего. Для трёх любых случайных событий А В и С:

N (A,~B) + N (B,~C) >= N (A,~C)

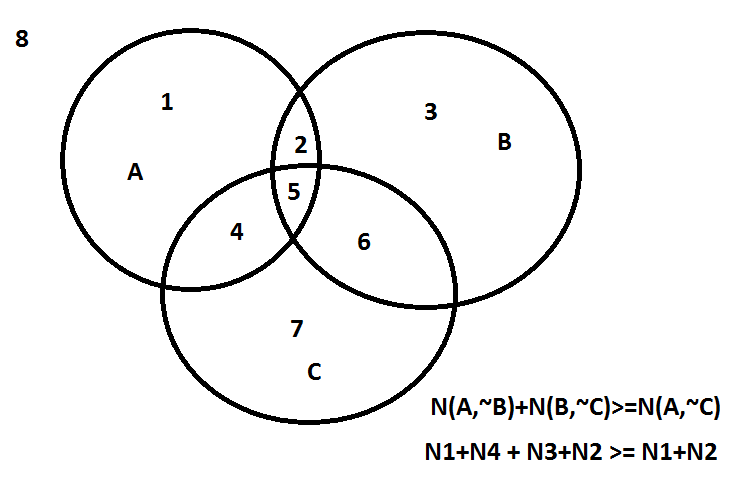
Если из картинки не все понятно, подробности можно найти на Лурке.

В нашем случае, А соответствует «фотон, который может пройти поляризатор -10°»
~А — отрицание А (фотон не может пройти -10°)
В — может пройти 0°
~В — не может пройти 0°
С — может пройти 10°
~С — не может пройти 10°

Не забывайте, мы предположили, что вышеперечисленное — это объективные скрытые свойства фотона, определяющиеся раз и навсегда после излучения.

Тогда:

N (A,~B) — количество фотонов, которые проходят через -10° и не проходят через 0°. Это ровно те фотоны, которые пошли через левый поляризатор в положительных исходах эксперимента 1. Ведь мы знаем что они проходят -10°. И мы также знаем они не проходят через 0°. Почему? Потому что их запутанные пары через 0° отлично проходят.

Аналогично:

N (B,~C) — фотоны, которые пошли через левый поляризатор в положительных исходах эксперимента 2 (проходят через 0° и не проходят через 10°).

N (A,~C) — фотоны, которые прошли через левый поляризатор в положительных исходах эксперимента 3 (проходят через -10° и не проходят через 10°)

Подставив в неравенство Белла статистику наших положительных исходов:

1,5% + 1,5% >= 5,8%

мы увидим что оно очевидно нарушается. Значит теория скрытых параметров не может быть верной. И у фотона нет объективной поляризации, до тех пор пока мы ее не померим.

Обходимся без неравенства Белла

Можно придти у тому же выводу и без использования математических теорем. Доказательство будет менее строгим, но более наглядным. Скрытые параметры двух запутанных фотонов без ограничения общности можно представить в виде таблицы:

«Угол поляризатора» → «Какой из двух фотонов проходит»
(Один и тот же угол проходит ровно один из двух фотонов)

Например:

Допустим, при рождении фотоны как-то «договариваются» между собой, заполняя эту таблицу. Потом копия таблицы остаётся у каждого из фотонов, и при измерении фотоны с ней «сверяются».

Очевидно, такая таблица должна:

• Содержать все возможные углы (фотоны «не знают» заранее как их будут мерить)

• Быть детерминированной. Процедура ее генерации может быть случайной, но после того как фотоны разлетелись, значения должны зафиксироваться. (Ситуация когда оба запутанных фотона пройдут/не пройдут один и тот же угол должна быть исключена.)

• Содержать одинаковое количество «левый» и «правый» (вероятность прохождения для случайного поляризатора — ½)

Рассмотрим положительные результаты экспериментов выше. О чем «договорились» фотоны в них? Большая часть таблицы скрыта от нас, но кое-что мы знаем:  

Таблица для эксперимента 1

Таблица для эксперимента 2

Таблица для эксперимента 3

Что произошло бы, если бы мы померили последнюю пару фотонов под углом 0°?   Другими словами, каково значение в их таблице для 0°? Мы не знаем. Но мы знаем что возможны ровно 2 варианта.

Вариант 3а

Такая пара фотонов также даст положительный результат в эксперименте 1, сравните таблицы!

Вариант 3 б

Также даст положительный результат в эксперименте 2

Итак, любая пара фотонов, которая положительна в эксперименте 3 также положительна либо в 1, либо в 2. Но это противоречит их вероятностям!

Судя по эксперименту 3, доля фотонов удовлетворяющих 3а или 3 б равна 5.8%. Но судя по 1 и 2 эта доля не может быть больше 3%. Мы снова пришли к противоречию.

Бонус — альтернативная интерпретация

Мы вынуждены вернуться к квантовому объяснению для поведения фотонов. Но можно ли как-нибудь избавится от его проблем? Я имею в виду мгновенное взаимодействие фотонов на разных концах вселенной и неустранимую случайность. Оказывается можно, но способ вам может не понравиться :)

Один из вариантов полностью локального, детерминированного и линейного объяснения всего происходящего называется «многомировая интерпретация квантовой механики».

В каком-то смысле, ММИ подразумевает откат к постулату «свет это волна». У электромагнитного поля есть волновая функция, которая определяет его поведение в пространстве и времени. «Фотонами» являются высокие гребни в этой функции, где энергия поля выше базового уровня. Они распространяются в пространстве по (приблизительно) прямым линиям со скоростью (приблизительно) с=299792458 м/с. Они могут взаимодействовать с другими аналогичными полями (электронным, кварковым, итп), и немного сами с собой.

Когда фотон достигает поляризатора, некоторая его часть (детерминированная для данного поляризатора) проходит сквозь него, а остаток поглощается. И то, и другое происходит одновременно.

Теперь важный момент. Подобно тому как два фотона могут запутаться друг с другом (так чтобы их импульсы не противоречили законам сохранения), фотон может запутаться с частицами поляризатора. Например если фотон прошёл, то импульс поляризатора останется неизменным, а если поглотился то импульс изменится. Оба состояния поляризатора являются реально существующими, так же как и оба состояния фотона. Но они зависят друг от друга (запутаны).

Дальше во взаимодействие вовлекается детектор частиц, который одновременно срабатывает и не срабатывает (запутанно с предыдущими альтернативами). Дальше запутывается лампочка на детекторе. Глаз ученого-физика, который видит свет лампочки. Его мозг который думает «фотон прошёл». Его рука, которая пишет в лабораторном журнале «фотон прошёл» (и одновременно «не прошёл»). Все это возможно потому, что одиночные фотоны, поляризаторы, детекторы, учёные-физики и их лабораторные журналы состоят по сути из одних и тех же частиц, подчиняющихся одной и той же квантовой физике, неотъемлемой частью которой является запутывание.

Наше сознание полностью определяется состоянием нейронов и атомов внутри них, следовательно оно не может воспринимать одновременно 2 разных состояния нашего мозга. Поэтому мы вынуждены случайно «переключиться» на одно из них. А это приводит к тому, что мы воспринимаем фотоны как неделимые частицы, которые обнаруживаются детекторами либо полностью, либо никак. Можно упрощённо сказать, что в момент когда фотон проходит поляризатор, вселенная разделится на две части (следуя за волной все увеличивающейся запутанности). Но на самом деле со вселенной ничего особенного не происходит, она просто меняется во времени, детерминировано и линейно, в соответствии с квантовыми законами. Это мы, как сознательные наблюдатели, вынуждены случайно выбирать нашу субъективную точку зрения на происходящее.

Здесь важно подчеркнуть. Сознательные наблюдатели — «особенные» (по сравнению с другими физическими объектами) не потому что они подчиняются какой-то особой физике, и поэтому магически вызывают коллапсы ВФ/«ветвления» вселенных/<подставьте другую интерпретацию>. Как раз наоборот. Все объекты во вселенной (включая человеческий мозг) могут запутываться и находиться сразу в нескольких состояниях в конкретный момент времени. Для всех объектов во вселенной (включая человеческий мозг) «остальная» вселенная будет выглядеть по-разному, в зависимости от конкретного состояния. Ни один объект во вселенной (включая человеческий мозг) в конкретном состоянии не может взаимодействовать сразу с несколькими «остальными» вселенными. Наше сознание материально и жестко привязано к конкретному состоянию частиц мозга. Поэтому оно может взаимодействовать только с одной «внешней» вселенной из множества реально существующих.

Как сценарий с двумя фотонами летящими в разные концы вселенной будет выглядеть в ММИ?

• пара запутанных фотонов излучается и разлетается в разные стороны
  Они летят пару миллиардов лет без взаимодействий и оказываются на разных концах вселенной

• 2 профессора физики из разных галактик, по имени L и R, ставят на их пути поляризаторы ориентированные параллельно друг другу
  Фотоны одновременно достигают поляризаторов (в одной из систем отсчета!). В других системах, L может получить фотон как раньше, так и позже R (из-за относительности одновременности) — это не имеет значения

• Профессор L вместе со своими поляризаторами, детекторами и всей лабораторией переходит в запутанное состояние: L1, который увидел что фотон прошёл, и L2, который увидел что фотон поглотился. То же самое происходит с профессорами R1 и R2.

• Каждый из 4-х профессоров не может наблюдать собственную запутанность, но тем не менее каждый реально существует для некоторого внешнего наблюдателя (при условии что наблюдатель ещё не запутан с результатами эксперимента).

• Все 4 профессора пока не взаимодействовали друг с другом. Либо в силу расстояния (как L1 и R2), либо в силу взаимоисключающих состояний волновой функции (как L1 и L2).

• Допустим профессоры (все 4) решают выяснить, какой результат получил их удалённый коллега. Для этого им придётся подождать минимум 4 миллиарда лет, но они не торопятся.

• Каждый посылает радиосигнал в другую галактику. Естественно, радиосигнал тоже будет запутан с соотвествующим исходом эксперимента. 

• И только в этот момент выяснится, что профессор L1 не может получить сигнал от R1 (и увидеть, что оба фотона прошли), он может получить сигнал только от R2 (у которого фотон поглотился). Потому что L1 запутан «не с той» частью волновой функции.

• Через 6 миллиардов лет, возмущение в ней наконец успело обойти обе галактики, и затронуло обе лаборатории в обоих состояниях. И поэтому состояние окончательно разделилось на связную область с профессорами L1+R2 и связную область L2+R1. Только эти пары профессоров могут между собой коммуницировать.

• Ещё раз подчеркну, что обе пары все ещё реально существуют и «доступны» для любого наблюдателя, который ещё не взаимодействовал с ними (например потому, что находится на расстоянии 7 миллиардов световых лет)

• Правда как только взаимодействие состоится, наблюдатель субъективно увидит только одну из пар, и заранее нельзя сказать какую.

В описании выше нет ни одного «моментального» взаимодействия на расстоянии. И нет объективной случайности (только субъективная, для сознательных наблюдателей). 

ММИ представляется мне более удобной для анализа на качественном уровне различных квантовых «парадоксов», вроде эксперимента с отложенным выбором. Количественные вычисления в ней делать наверное сложнее, но мне они не нужны, я же не физик. :) Свои проблемы в ММИ тоже имеются. В общем это вопрос личных предпочтений. Эксперименты, позволяющие различить ММИ от других интерпретаций вроде как теоретически возможны. Но на практике до этого ещё очень далеко.

Надеюсь, что независимо от вашей предпочтительной интерпретации КМ, статья прояснила некоторые особенности экспериментов с поляризацией запутанных фотонов. И на роль неравенств Белла в этом процессе.