Непростые простые числа: секреты тайного общества ткачей

Автор статьи предлагает заглянуть в то, что представляют собой множества простых чисел, если взглянуть на них геометрическим образом. Это не профессиональная работа, а простое, любительское исследование некоторых любопытных закономерностей. Поэтому, в статье не будет сложной математики, и мы не будем забираться глубоко в ее дебри.
Вероятно, читателю известны многие проблемы, связанные с простыми числами. Их расположение в множестве натуральных чисел неочевидно. Большие простые числа трудно находить, нужно много усилий, чтобы проверить большое число на простоту. На этой трудности основаны многие современные методы криптографии. Мы можем легко перемножить да многозначных простых числа, но зная результат найти исходные множители — очень сложная задача.
Есть множество способов оптимизации, которые намного быстрее простого перебора, однако даже если оптимизация ускорит поиск в 10 раз, достаточно увеличить число на 2–3 десятичных знака (например, в 100 раз), чтобы замедлить поиск в 10^100 раз.
Это и значит, что сложность алгоритма является экспоненциальной, и поэтому какой бы быстрый ни был суперкомпьютер, мы можем подобрать длину числа еще больше, чтобы таких суперкомпьютеров потребовалось миллиард. Правда, стоит уточнить еще раз: находить простые числа для перемножения при этом становится так же все труднее и труднее.
К слову, математики не нашли ни доказательства, ни опровержения того, что нельзя найти алгоритм факторизации, сложность которого не была бы экспоненциально зависящей от длины числа. А доказав или опровергнув это, можно, заодно, решить математическую проблему, известную как гипотеза Римана. За ее доказательство математический институт Клея обещает миллион долларов.
Раз уж мы не знаем закономерности, по которой бы легко находились простые числа, может быть, посмотрим внимательнее на закономерности чисел составных? Говоря математически, рассмотрим множество натуральных чисел, дополнительное к множеству простых.
Идея составных чисел очень проста. Возьмем несколько натуральных чисел и перемножим их. Тем самым, мы получаем составное число.
Мы легко найдем бесконечность составных чисел, просто умножив n на 2.
То же касается умножения на 3.
Далее следует 4, но здесь мы новых чисел не найдем, все они уже равны 2n. Далее следуют 5n, потом 6n, которые нами найдены уже дважды, как 2n и 3n одновременно. Это не увеличивает количества составных чисел, но наводит нас на мысль, что закономерность составных чисел заключена в произведении простых.
Но если мы пройдем немного дальше, то обнаружим интересную закономерность: число 6 это произведение 2 и 3. Это значит, что у нас будет сразу много удобно расположенных в таблице составных чисел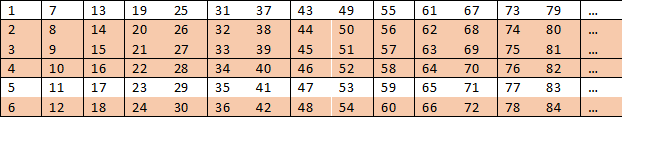
Глядя на таблицу, мы понимаем, что в строках 2, 3, 4 и 6 никогда не может быть простых чисел. А это значит, что вероятность найти простое число не может превышать 2/6. Мы понимаем, что чисел эта вероятность еще меньше, но как сильно?
Попробуем и дальше поискать удобную структуру составных чисел, а для этого, подумаем, что значит 2×3=6? Что если мы возьмем произведение из 2×3х5 за основу? Мы получаем следующую интересную таблицу (чтобы она не занимала много места, уменьшим шрифт)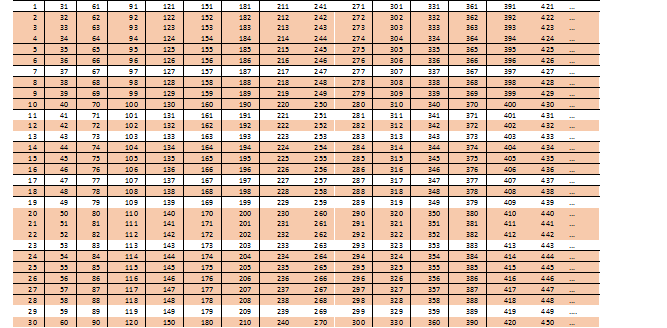
Мы видим, что— 15 строк вида 2n, — 5 строк вида 3n (плюс 5 вида 6n уже учтены в 2n)— и 2 строки вида 5n (еще три вида 10n уже вычеркнуты в числах 2n и одна 15n среди строк 3n)не могут содержать простых чисел (мы же этого и ожидали, верно?)
Остаются лишь восемь строк вида 30n + i, где i = 1, 7, 11, 13, 17, 19, 23, 29. Если приглядеться, в них можно увидеть симметрию. 1+29=7+23=11+19=13+7.
Поэтому компактно можно записать как 30n ± i, где i = 1, 7, 11, 13,17
И мы понимаем, что вероятность найти произвольное простое число не больше 8/30. На 2/30 стало меньше…
Что же дальше? Следуя логике, в следующей таблице должно быть 2×3х5×7=210 строк. Еще дальше 210×11=2310, потом 2310×13, и так мы будем последовательно перемножать простые числа, получая все большую и большую базу «строчной развертки», которая будет сохранять свою полосатость.
Это выглядит так, будто бы простые числа отбрасывают «тени» в бесконечность кратных им чисел, если их располагать в ряд соответственно базе числа, обозначим его П (i), равного последовательному произведению i простых чисел.
Можно заметить, что полоса строк, лежащих между первой и следующей, где могут содержаться простые числа, растет по очень простому закону: если строк 6, то есть 2×3, то простые числа могут быть в строке 5, если 2×3х5, то начиная со строки 7, что логично. Таким образом, в матрице с количеством строк 30 030 (2×3х5×7х11×13) после первой строки будет широкая полоса составных чисел, до строки, следующей от числа 17. А если мы возьмем матрицу на 9 699 690 строк (2×3х5×7х11×13х17×19), то полоса, где простых чисел нет, протянется до строки 21. Что характерно, из-за симметрии, внизу матрицы так же будет 20 строк с исключительно составными числами.
Но что такое эти произведения? 2×3 — это прямоугольник, площадью 6. 2×3х5 — параллелепипед, объемом 30. А дальше? 2×3х5×7 — гиперпараллелепипед в 4 измерениях, с гиперобъемом 210? А потом? 5 измерений, 6, … Бесконечность?
Только подумайте, что могли бы себе вообразить многомерный мир, в которых простые числа отбрасывают свои тени во всех измерениях…
Мы можем представить себе четыре и более измерений, проекциями их на плоскость или в трехмерное пространство, например, раскладывая матрицу, словно перекатывая многомерный гиперкуб с грани на грань и рассматривая получающиеся на бумаге отпечатки (а так же получая отпечатки сечений)Вот начальная грань
А вот ее развертка с двух сторон
Очень удачно, что во всей правой гиперплоскости у нас исключительно составные числа. Можем в нее даже не путешествовать. Можно взглянуть и на другую развертку, взгляд «сверху», но далее мы пойдем в более интересном направлении.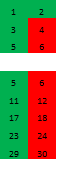
Попробуем теперь развернуть картинку в четвертое измерение, в интересующую нас сторону, где можно находить простые числа
Здесь коричневым цветом обозначены числа вида mn, которые составлены произведениями чисел от 11 до 19 (ближайшее целое, меньшее 210/11). Особенность этих чисел в том, что они сами не являясь простыми числами не «отбрасывают тени» вглубь следующего измерения.
Как мы видим, средний слой развертки снова становится тривиальным — здесь и далее простых чисел нет. А вот внешние грани гиперпаллелепипеда можно рассматривать и дальше. Каждый столбец раскладывается в матрицу 7×11, получаем 5 таких матриц для каждого из трех слоев матрицы 3×5 (здесь показана развертка одного столбца и фрагмент матрицы для второго столбца)
Дальше углубляться в измерения на примере развертке мы не будем, в рамках статьи было бы неблагоразумно. В конце статьи Вы можете посмотреть на еще несколько иллюстраций. Надеюсь, это исследование немножко разбудило Ваше воображение, и путешествие в мир непростых и простых чисел Вам понравилось и показалось полезным.
В дополнение, автор хочет заметить, что продолжает исследование этого метода. Например, вопросы появления в более крупных матрицах произведений третьих, четвертых и далее степеней чисел, которые добавляют все новые простые числа в глубоких и объемных проекциях, как отбрасывающих тень в следующие измерения, так и остающиеся «точечными» вкраплениями.
Но, пожалуй, наибольший интерес вызывает возможность уточнения оценки вероятности нахождения простых чисел все дальше и дальше. Если рассматривать матрицы, то мы видим, как вероятность падает, начиная с 4/6, далее до 7/24 (или усредненно 11/30), потом 36/180 (или 47/210), и т.д.
Кроме того, у автора есть алгоритм факторизации, оптимизация которого в многомерной матрице может заметно его ускорить (но он от этого не перестает иметь экспоненциальную степень сложности от количества знаков разлагаемого числа).
Сам алгоритм в основе очень прост.
Берем два последовательные нечетные числа, p и q, такие, что pq близко к X (используется округление корня из X до большего и меньшего нечетных чисел, при условии, что Х не является квадратом). Предварительно мы устраняем четность Х (делим на 2 до тех пор, пока результат четный), получая множитель 2^K. Далее же, в цикле, проверяем разницу между Х и pq. Если она равна нулю — результат получен. Если она больше нуля, мы уменьшаем q на 2. Если меньше нуля, увеличиваем p на 2q. В цикле используется только сложение, поэтому алгоритм довольно быстрый (зависит лишь от реализации функций работы с BigInteger)
Однако, у автора есть гипотеза, что шаг пересчета можно значительно увеличить, не теряя в аккуратности, если использовать базу кратности. Всякое число Х находится между двумя последовательными П (i) и П (i+1), где П (i) — произведение первых i простых чисел, поэтому можно определить, к какому из ребер число Х находится ближе и какой диапазон свободы у p и q в каждой из проекций) и тем самым образуемый p и q прямоугольник из одной плоскости развернуть в сечение гиперпараллелепипеда.
P.S. А при чем здесь тайное общество ткачей, спросит читатель, которого привлек оригинальный заголовок? Возможно, читатель помнит фильм «Особо опасен» В этом году обещают даже продолжение… В этом фильме ткацкий станок делает предсказания, укладывая нити и узелки… Посмотрите, как похоже это делают ниточки простых чисел…
В матрице 30×7
И кусочек матрицы 210×11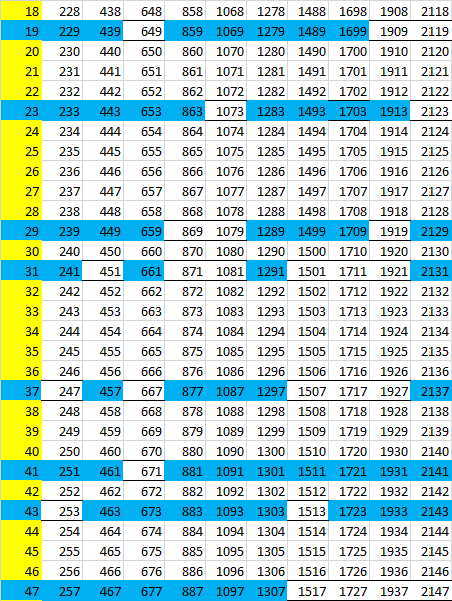
А управляют узелками этой машиной вот такие матрицы-перфокартыРазвертка матрицами 2×3

И побольше, матрицами 6×5
