Непересекающиеся множества и загадочная функция Аккермана19.10.2015 13:03

Речь пойдёт о простой структуре данных — системе непересекающихся множеств. Вкратце: даны непересекающиеся множества (например, компоненты связности графа) и по двум элементам x и y можно: 1) узнать, находятся ли x и y в одном множестве; 2) объединить множества, содержащие x и y. Сама структура очень проста в реализации и описывалась много раз в различных местах (например, есть хорошая статья на хабре и ещё кое-где). Но это один из тех удивительных алгоритмов, написать который ничего не стоит, а вот разобраться, почему он работает эффективно совсем нелегко. Я постараюсь изложить относительно простое доказательство точной оценки на время работы этой структуры данных, придуманное Зейделем и Шариром в 2005 (оно отличается от того ужаса, который многие могли видеть в других местах). Конечно, сама структура тоже будет описана, а попутно разберёмся причём здесь обратная функция Аккермана, о которой многие знают только, что она оооочень медленно растёт.

Система непересекающихся множеств

Представьте, что вам по каким-то причинам пришлось поддерживать множество из n точек с двумя запросами: Union(x,y), который соединяет точки x и y ребром, и IsConnected(x,y), который по точкам x и y проверяет, можно ли из x по рёбрам пройти в y. Как решать такую задачу?

Во-первых, разумно думать не о точках, а о компонентах связности. Компонента связности — это множество точек, в котором из каждой точки можно по рёбрам пройти в каждую другую из того же множества. Тогда Union(x,y) — это просто объединение компонент, содержащих x и y (если они не в одной компоненте), а IsConnected(x,y) — это проверка, находятся ли x и y в одной компоненте.

Во-вторых, удобно выбрать в каждой компоненте одну особую выделенную вершину взятую наугад. Пусть Find(x) возвращает выделенную вершину из компоненты, содержащей x. С помощью Find(x) функция IsConnected(x,y) сводится к простому сравнению Find(x) и Find(y): IsConnected(x,y) == (Find(x)==Find(y)). Когда две компоненты объединяются в одну с помощью Union, выделенная вершина одной из объединяемых компонент перестаёт быть выделенной, потому что выделенная вершина в одной компоненте всегда одна.

Итак, мы абстрагировались от исходной задачи и свели её к решению другой, более общей задачи: у нас есть набор непересекающихся множеств, которые можно объединять с помощью Union и в которых есть выделенный элемент, получаемый с помощью Find. Формально структуру можно описать так: есть изначальный набор одноэлементных множеств {x1},{x2},...,{xn} с такими операциями:

Union(x, y) сливает вместе множества, содержащие элементы x и y;
Find(x) возвращает выделенный элемент из множества, содержащего элемент x, т.е. если взять любой y из того же множества, что и x, то Find(y) = Find(x). Find нужен, чтобы можно было узнавать, находятся ли два элемента в одном и том же множестве.

Системы непересекающихся множеств, а точнее та их реализация о которой пойдёт речь далее, придуманы ещё на заре компьютерных наук. Иногда эту структуру называют Union-Find. У систем непересекающихся множеств немало приложений: они играют центральную роль в алгоритме Краскала для поиска минимального остова, используются в построении так называемого дерева доминаторов (естественная штука при анализе кода), позволяют легко следить за компонентами связности в графе и т.д. Сразу скажу, хоть эта статья и содержит краткое описание реализации самой структуры непересекающихся множеств, для развёрнутого обсуждения приложений этих структур и деталей реализации лучше почитать уже приводившиеся источники на хабре и у Максима Иванова. Но мне всегда было интересно узнать, как получается та необычная оценка на время работы систем непересекающихся множеств, которую даже понять не так-то просто. Итак, главная цель этой статьи — теоретическое обоснование эффективности структур Union-Find.

Как же реализовать множества с операциями Union-Find? Первое, что приходит в голову — это хранить множества ввиде направленных деревьев (см. рисунок). Каждое дерево — это множество. Выделенный элемент множества (тот, который возвращает функция Find) — это корень дерева. Чтобы слить деревья, надо просто прицепить корень одного дерева к другому.

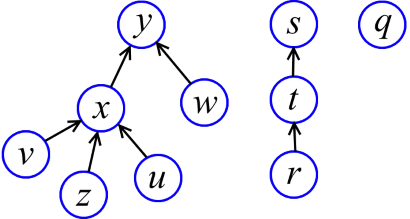
Find(x) просто поднимается от x по стрелкам, пока не достигнет корня, и возвращает корень. Но если оставить всё как есть, то будут легко получаться «нехорошие» деревья (типа длинной «цепи»), на которых Find тратит много времени. То есть, «высокие» деревья нам ни к чему.

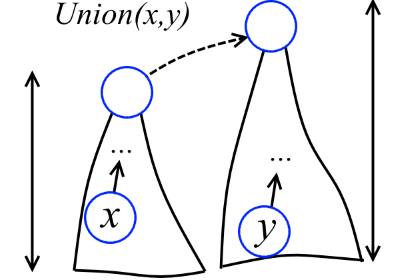
Высота вершины x — это максимальная длина пути от какого-то листа до x. Например, на рисунке выше высота y - 2, x - 1, z - 0. Немного поразмыслив, можно снабдить каждую вершину высотой. Будем называть эти высоты рангами (забегая вперёд, скажу, что эти штуки не называются высотами, как полагается, потому что в дальнейшем деревья будут перестраиваться и ранги уже не будут в точности соответствовать высотам). Теперь при объединении двух деревьев более низкое дерево будет подцепляться к более высокому (см. рисунок ниже).

Реализуем это! Узлы-элементы определим так:

struct elem {
  elem *link; //указатель на родителя узла
  int rank;    //ранг узла
  double value; //какое-то хранящееся значение элемента
};

Изначально для каждого элемента x выполняется x.link=0 и x.rank=0. Можно уже написать функцию объединения и предварительную версию функции Find:

void Union(elem *x, elem *y)
{
  x = Find(x);
  y = Find(y);
  if (x != y) {
    if (x->rank == y->rank)
      y->rank++;
    else if (x->rank > y->rank)
      swap(x, y);
    x->link = y;
  }
}
elem *Find(elem *x) //первая плохая версия Find
{
  return x->link ? Find(x->link) : x;
}

Даже такая реализация уже довольно эффективна. Чтобы это увидеть, докажем пару простых лемм.

Лемма 1. В реализации Union-Find с ранговой оптимизацией каждое дерево с корнем x содержит ≥2x->rank вершин.

Доказательство. Для деревьев, состоящих из одной вершины x, x->rank=0 и ясно, что утверждение леммы выполняется. Пусть Union объединяет деревья с корнями x и y, для которых утверждение леммы справедливо, т.е. деревья с корнями x и y содержат ≥2x->rank и ≥2y->rank вершин, соответственно. Проблема может возникнуть, если x присоединяется к y и ранг y увеличивается. Но это происходит только если x->rank == y->rank. Пусть r — ранг y до объединения. Значит, новое дерево с корнем y содержит ≥2x->rank + 2r = 2 2r = 2r+1 вершин. А это и требовалось доказать.

Лемма 2. В Union-Find с ранговой оптимизацией ранг каждой вершины x равен высоте дерева с корнем в x.

Доказательство. Когда алгоритм только начинает работу и все множества одноэлементны, для каждой вершины x->rank = 0, что несомненно является высотой. Пусть Union объединяет два дерева с корнями x и y и пусть высоты этих деревьев в точности равны соответствующим рангам x->rank и y->rank. Покажем, что и после объединения ранги равны высотам. Если x->rank < y->rank, то x будет подцеплен к y и, очевидно, высота дерева с корнем y не изменится; Union и правда не меняет y->rank. Случай x->rank > y->rank аналогичен. Если же x->rank == y->rank, то после присоединения x к y высота y увеличится на единицу; и Union как раз увеличивает y->rank на единицу. Что и требовалось.

Из леммы 1 следует, что ранг любой вершины не может быть больше log n (все логарифмы у нас по основанию 2), где n обозначает число элементов. А из леммы 2 отсюда следует, что высота любого дерева не превосходит log n. Значит, каждая операция Find выполняется за O(log n). Поэтому m операций Union-Find выполняются за O(m log n).

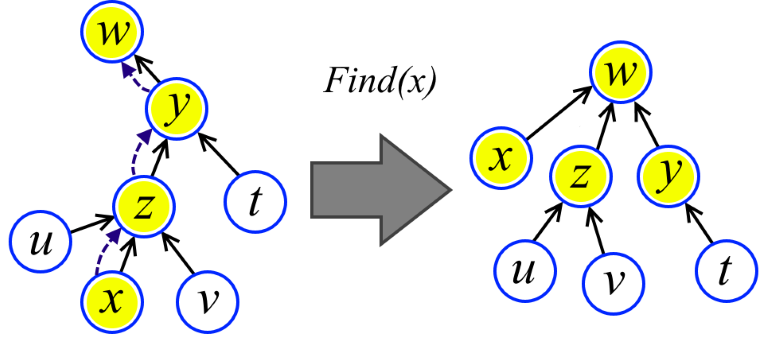
Можно ли ещё эффективнее? На помощь приходит вторая оптимизация. При выполнении подъёма в процедуре Find просто перенаправим все пройденные вершины в корень (см. рисунок). Хуже от этого точно не станет. Но оказывается станет гораздо лучше.

elem * Find(elem *x)
{
  return x->link ? (x->link = Find(x->link)) : x;
}

Итак, у нас есть последовательность из m операций Union и Find на n элементах и нужно оценить скольку времени она работает. Может быть это O(m log n)? Или O(m log log n)? Или всё таки O(m)?

Интуитивно кажется, что алгоритм со второй оптимизацией должен быть эффективнее. И так оно и есть, но вот доказать это уже не так-то просто. Немного по-анализировав, можно предположить, что алгоритм линеен, т.е. последовательность из m операций Union и Find вперемешку выполняется за O(m). Но как ни пытайтесь, доказать это строго не получится, потому что это не так. Первое полное доказательство точной верхней и нижней границ дал Тарьян в 1975 году и эта граница «почти» O(m), но, к сожалению, не O(m). Затем последовали работы, в которых было доказано, что получить O(m) в принципе нельзя. Честно сказать, я не смог разобраться во всём этом; даже контрпример, показывающий, что Union-Find работает медленнее, чем за O(m), довольно сложен для понимания. Но к счастью, в 2005 году Зейдель и Шарир получили новое относительно «понимабельное» доказательство верхней границы. Их статья называется «Top-down analysis of path compression». Именно их результат в ещё немного упрощённой форме здесь я и постараюсь изложить. Нахождение «понимабельного» доказательства нижней границы можно считать ещё нерешённой проблемой.

Так ли плохо, что у нас не срослось с O(m)? Вообще-то, всё это представляет только чисто теоретический интерес, потому что «почти» O(m), полученное Тарьяном, не отличимо от O(m) на всех мыслимых входных данных (скоро станет понятно почему). Сразу скажу, что доказательства того, что это не O(m) не будет (просто я сам его не вполне понимаю), поэтому может сложиться впечатление, что можно ещё чуть-чуть и… Но нельзя. По крайней мере, несмотря на некоторые неудавшиеся попытки, в работе Тарьяна и серии связанных работ найти критические ошибки не удалось.

Звёзды, звёзды, звёзды

Что же это за функции такие, которые дают «почти» O(m)? Рассмотрим какую-нибудь функцию f такую, что f(n) 1, но при этом f(n) стремится в бесконечность. Функция f растёт медленно: весь её график находится под графиком функции g(n) = n. Определим оператор итерации *, который делает из медленной функции f супер медленную функцию f*:

f*(n) = min{k: f(f(… f(n))) < 2, где f взято k раз}

То есть f*(n) показывает сколько раз надо сжимать число n операциями f(n) > f(f(n)) > f(f(f(n))) > ..., чтобы получить константу меньше двух.

Пару примеров, чтобы освоиться. Если f(n) = n-2, то f*(n) = [n/2] (целая часть от деления на два). Если f(n) = n/2, то f*(n) = [log n] (целая часть двоичного логарифма). Если f(n) = log n, то что же такое f*(n) = log* n? Функцию log* n называют итерированным логарифмом. Чуть-чуть порасписывав на бумаге, можно доказать, что log* n = O(log log n), log* n = O(log log log n) и вообще log* n = O(log log… log n) для любого числа логов. Чтобы вообразить насколько медленный итерированный логарифм, достаточно взглянуть на значение log* 265536 = 5.

В дальнейшем будет показано, что время выполнения m операций Union-Find можно оценить как O(m log* n) и, более того, можно вывести оценки O(m log** n), O(m log*** n) и так далее до некоторой предельной функции O(m α(m,n)), определённой ниже. Вообще, я полагаю, что для современных практических применений O(m log log n) почти не отличимо от O(m). А O(m log* n) вообще не отличимо от O(m), что и говорить про O(m log** n) и другие. Теперь можно представить, почему речь идёт о «почти» O(m).

Оценка O(m log* n)

Получение оценки O(m log* n) является основной частью доказательства. После этого почти сразу будет получена точная оценка. Чтобы было проще, примем одно несущественное допущение: m ≥ n.

Не ограничивая общности рассуждений, будем считать, что операция Union всегда принимает на вход «корни» множеств, т.е. Union вызывается так: Union(Find(x), Find(y)). Тогда Union выполняется за O(1). Это ограничение тем более естественно, потому что Union(x,y) первым делом как раз вызывает Find(x) и Find(y). Значит, при анализе нас будут интересовать только операции Find.

Продолжим упрощать. Представим, что операции Find вообще не выполняются и пользователь как-то сам угадывает, где корни множеств. Последовательность Union-ов строит лес F (лес — это множество деревьев). По лемме 2 в F ранг каждой вершины x — это высота поддерева с корнем в x. Отсюда следует, что ранг каждой вершины меньше ранга родителя этой вершины. Для нас это наблюдение важно.

Вернём теперь последовательность Find-ов в строй. Можно представлять себе, что первый Find пробегает по какому-то пути в F и выполняет операцию сжатия пути в F, при которой каждая вершина пути становится отпрыском вершины в «голове» пути (см. рисунок). При этом голова пути это совсем не обязательно корень F. Другими словами, условимся, что в каком-то смысле все Union были выполнены заранее, а теперь на лесе F выполняются сжатия путей, соответствующих Find при нормальном ходе алгоритма. Затем второй Find пробегает по какому-то пути уже в модифицированном лесе (в исходном лесе F этот путь мог вообще ещё не существовать) и опять выполняет сжатие пути. И так далее.

Важно отметить, что после сжатия пути ранги не меняются. Поэтому мы называем ранги рангами, а не высотами, потому что в модифицированном лесе ранги уже могут не соответствовать высотам.

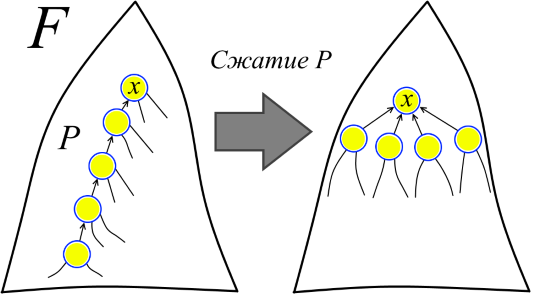
Теперь можно чётко сформулировать, что мы доказываем. Есть последовательность лесов F = F1, F2, ..., Fm и последовательность сжатий путей P1, P2, ..., Pm в лесах F1, F2, ..., Fm, соответственно. Сжатие пути P1 в лесу F1 получает лес F2, сжатие пути P2 в F2 получает F3 и так далее. (Причём, например, путь Pk мог ещё не существовать в лесу F и появился только после сжатия путей P1, P2, ..., Pk-1) Необходимо оценить сумму длин путей P1, P2, ..., Pm (длина пути — это количество рёбер в пути). Так мы получим оценку на время выполнения m операций Find, потому что длина сжимаемого пути — это как раз число операций «перелинковки» вершин в соответствующем Find.

Вообще-то, мы вознамерились доказывать даже более общее утверждение чем необходимо, ведь не каждая последовательность сжатий путей соответствует последовательности операций Union-Find. Но эти нюансы нас не интересуют.

Итак, есть лес F и последовательность сжатий путей в нём в том смысле, который придавался этому выше, т.е. есть последовательность лесов F = F1, F2, ..., Fm и последовательность сжатий путей P1, P2, ..., Pm в них. Пусть T(m,n) обозначает сумму длин сжимаемых путей P1, P2, ..., Pm в самом худшем случае, когда сумма длин P1, P2, ..., Pm максимальна. Задача — оценить T(m,n). Это чисто комбинаторная задача и все нетривиальные доказательства эффективности Union-Find естественным образом так или иначе сводятся к этой конструкции.

Оценка длин сжимаемых путей

Первый существенно нетривиальный шаг в рассуждении — введение дополнительного параметра. Рангом леса F будем называть максимум среди рангов вершин F. Через T(m,n,r) обозначим, аналогично T(m,n), сумму длин сжимаемых путей P1, P2, ..., Pm в самом худшем случае, когда сумма длин P1, P2, ..., Pm максимальна, а исходный лес имеет ранг не больше r. Ясно, что T(m,n) = T(m,n,n), потому что ранг любого леса с n вершинами меньше или равен n. Параметр r понадобится для рекурсивного сведения задачи оценки для леса F к подзадачам на подлесах F.

Обозначим d = log r. Разделим лес F на два непересекающихся леса F+ и F-: «верхний лес» F+ состоит из вершин с рангом >d, а «нижний лес» F- состоит из всех остальных вершин (см. рисунок). Это разбиение было подмечено ещё в первых доказательствах оценок на Union-Find в связи со следующим фактом: оказывается, верхний лес F+ содержит существенно меньше вершин чем F-.

Основная идея состоит в том, чтобы оценить грубо длины сжатий путей, лежащих в F+ (это можно будет сделать, потому что F+ очень мал), а затем рекурсивно оценить длины сжатий путей в F-. То есть, неформально, наша цель — вывод рекурсии T(m,n,r) ≤ T(m,n,d) + (длины путей, не вошедших в F-). Начнём двигаться к этой цели с формализации того, что же означает, что F+ «очень мал». Обозначим через |F'| число вершин в произвольном лесе F'.

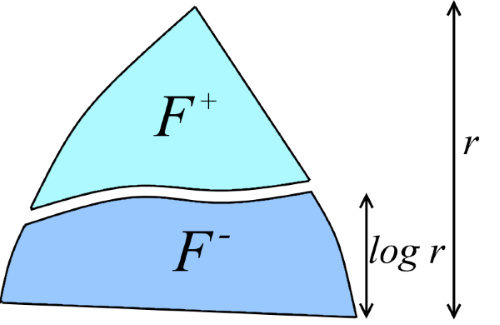
Лемма 3. Пусть F+ — лес, состоящий из вершин F ранга >d. Тогда |F+| < |F| / 2d.

Доказательство. Зафиксируем какое-то t > d. Оценим сколько в F+ вершин ранга t. В F по лемме 2 ранг вершины равен высоте дерева с корнем в данной вершине. Значит, родитель вершины с рангом t обязательно имеет ранг >t. Таким образом, поддеревья F с корнями с рангом t не пересекаются (см. рисунок ниже). Дерево с корнем с рангом t по лемме 1 содержит ≥2t вершин. Значит, всего существует ≤n/2t вершин с рангом t. Пробегая t по d+1, d+2, ..., получаем, что число вершин в F+ ограничено сверху бесконечной суммой n/2d+1 + n/2d+2 + n/2d+3 +… По формуле суммирования геометрической прогрессии получаем, что эта сумма равна n/2d. Что и требовалось.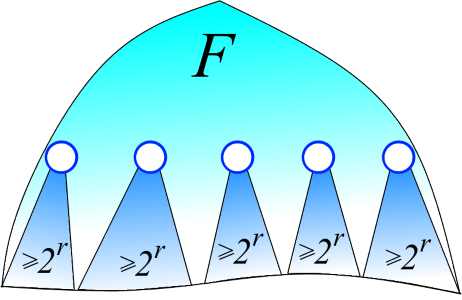

Отсюда и далее для краткости будем обозначать n+ = |F+| и n- = |F-|.

Второй нетривиальный шаг в рассуждении. Разобьём множество путей P1, P2, ..., Pm на три подмножества (см. рисунок):

P+ — пути, целиком содержащиеся в F+;
P- — пути, целиком содержащиеся в F-;
P+- — пути, имеющие вершины и из F+, и из F-.

Каждый путь из множества P+- разбивается на два пути: верхний путь в F+ (белые вершины на рисунке ниже слева) и нижний путь в F- (зелёные вершины на рисунке ниже слева). Верхние пути мы просто засунем в множество путей P+. Обозначим через m+ число путей в полученном таким образом множестве, т.е. m+ = |P+| + |P+-| (в отличие от аналогичного обозначения |F'| для лесов, |P| обозначает число путей в множестве P, а не суммарное число вершин в них). Обозначим m- = |P-|. Тогда:

T(m,n,r) ≤ T(m+, n+, r) + T(m-, n-, d) + (сумма длин нижних частей путей из P+-).

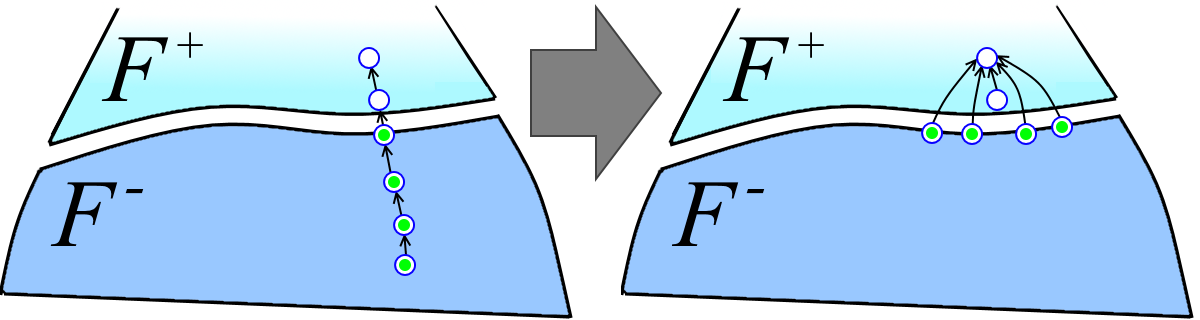
Оценим сумму длин нижних частей путей из P+-. Пусть P — нижняя часть пути из P+- (зелёные вершины на рисунке выше). Все вершины в P, кроме головной, до перелинковки имели родителей из F- (головная обязательно имеет родителя из F+), а после перелинковки имеют родителя из F+ (см. рисунок выше). Значит, каждая вершина из F- может участвовать в какой-то нижней части пути из P+- в качестве неголовной только лишь один раз. Получается, что сумма длин нижних частей путей из P+- меньше или равна |P+-| + n- (по единице на каждую головную вершину плюс по единицы на каждую вершину из F-). Заметим, что |P+-| ≤ m+. Значит, сумма длин нижних частей путей из P+- не превосходит m+ + n-.

Важное замечание: в проделанных рассуждениях было неважно, что ранг F- меньше или равен d = log r; вместо log r могло быть любое другое значение. Если вы добрались до этого места, то поздравляю, мы только что доказали центральную лемму.

Центральная лемма. Пусть F+ — лес вершин из F с рангами >d, а F- — лес остальных вершин из F. Обозначения m+, m-, n+, n- определены по аналогии. Тогда справедлива рекурсия: T(m,n,r) ≤ T(m+, n+, r) + T(m-, n-, d) + m+ + n-.

Как уже упоминалось, поскольку лес F+ очень мал, длины путей в нём можно оценивать грубыми методами. Проделаем это. Очевидно, что сжатие пути длины k в F+ выполняет перелинковку k-1 вершины; то есть k-1 вершина «поднимается» вверх по дереву. Высота F+ не превосходит r и поэтому каждая вершина может подниматься не более r раз. Значит, m+ сжатий путей выполняют самое большее rn+ перелинковок (т.е. «подъёмов» вершин). Отсюда заключаем, что сумма длин m+ сжатий путей в F+ ограничена сверху числом rn+ + m+ (по единице на каждый подъём вершины и по единице на голову каждого пути). По лемме 3 получаем rn+ ≤ rn/2d = rn/2log r = n. В итоге получаем T(m+, n+, r) ≤ n + m+. Применяя центральную лемму, выводим рекурсию:

T(m,n,r) ≤ T(m+, n+, r) + T(m-, n-, log r) + m+ + n- ≤
≤ n + m+ + T(m-, n, log r) + m+ + n =
= 2n + 2m+ + T(m-, n, log r).

Теперь рекурсивно продолжим действовать в том же духе на лесе F- так же, как действовали на лесе F, т.е. просто раскроем рекурсию:
T(m,n,r) ≤ (2n + 2m+) + T(m-, n, log r) ≤
≤ (2n + 2m+) + (2n + 2m0+) + T(m0-, n, log log r) ≤
≤ (2n + 2m+) + (2n + 2m0+) + (2n + 2m1+) + T(m1-, n, log log log r) ≤
≤…
Здесь m0+, m1+,… — это значения, соответствующие m+ на различных уровнях рекурсии. Ясно, что m+ + m0+ + m1+ +… ≤ m (см. рисунок ниже). Глубина рекурсии — это число раз, которое нужно прологарифмировать r, чтобы получить константу. Но это же log* r! В итоге выводим T(m,n,r) ≤ 2m + 2n log* r.

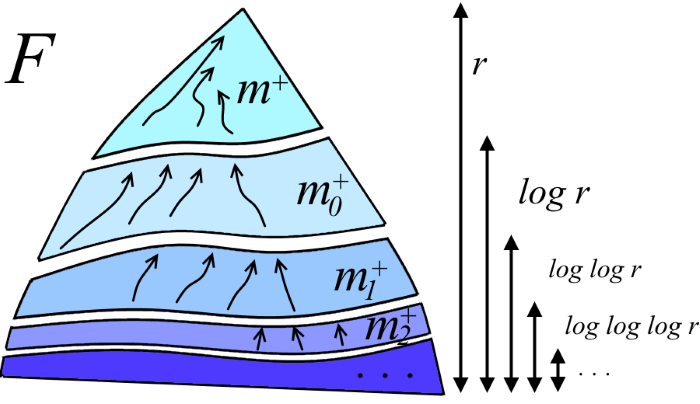
Окончательное решение с обратной функцией Аккермана

Если повнимательнее проанализировать полученные выводы, можно заметить, что в общем-то значение log r играло роль только в раскрытии выражения T(m+, n+, r), чтобы получить T(m+, n+, r) ≤ n + m+. Это достигалось с помощью леммы 3 и наивного рассуждения, доказывающего, что T(m+, n+, r) ≤ rn+ + m+. Но в предыдущем разделе мы получили оценку по-лучше: T(m+, n+, r) ≤ 2m+ + 2n+ log* r. Переопределим наших главных героев, «понизив» лес F-: F+ — это лес вершин F с рангом >log* r, а F- — лес оставшихся вершин с рангом ≤ log* r. По аналогии определим параметры m+, m-, n+, n-.

По лемме 3 получаем n+ < n/2log* r, т.е. лес F+ по-прежнему «маленький» по сравнению с F- (на первых порах мне это казалось даже контринтуитивным). В предыдущем разделе мы установили, что T(m+, n+, r) ≤ 2m+ + 2n+ log* r. Отсюда, учитывая, что 2(n/2x)x ≤ n для любого целого x ≥ 1, выводим T(m+, n+, r) ≤ 2m+ + 2(n/2log* r) log* r ≤ 2m+ + n. Это почти как оценка T(m+, n+, r) ≤ n + m+, полученная раньше! Применяя центральную лемму, получаем рекурсию:

T(m,n,r) ≤ T(m+, n+, r) + T(m-, n-, log* r) + m+ + n-.

Раскрывая T(m+, n+, r)≤ 2m+ + n, преобразуем рекурсию:

T(m,n,r) ≤ T(m+, n+, r) + T(m-, n-, log* r) + m+ + n- ≤
≤ 2m+ + n + T(m-, n-, log* r) + m+ + n- ≤
≤ 3m+ + 2n + T(m-, n, log* r).

Теперь раскроем пару уровней рекурсии:

T(m,n,r) ≤ (3m+ + 2n) + T(m-, n, log* r) ≤
≤ (3m+ + 2n) + (3m0+ + 2n) + T(m0-, n, log* log* r) ≤
≤ (3m+ + 2n) + (3m0+ + 2n) + (2m1+ + 2n) + T(m1-, n, log* log* log* r) ≤
≤...

Здесь, как и в прошлом разделе, m0+, m1+,… — значения, соответствующие m+ на различных уровнях рекурсии. Ясно, что m+ + m0+ + m1+ +… ≤ m. Глубина рекурсии равна log** r. В итоге T(m,n,r) ≤ 3m + 2n log** r. Очень недурная оценка. Но можно ли ещё разок проделать этот фокус, используя только что полученную оценку T(m,n,r) ≤ 3m + 2n log** r? Да!

Детали я на этот раз опущу. «Понизив» лес F- до ранга log** r, можно, опять используя лемму 3, получить T(m+, n+, r) ≤ 3m+ + n. Это почти как только что установленная оценка T(m+, n+, r) ≤ 2m+ + n. Затем с помощью этой оценки и центральной леммы выводим T(m,n,r) ≤ 4m + 2n log*** r.

Можно продолжить и далее, «понизив» F- до ранга log*** r. Вообще, проделав эту процедуру k раз для любого натурального k, можно получить такую оценку:

T(m,n,r) ≤ km + 2n log**...* r, где число звёзд равно k-1.

Осталось оптимизировать это рекуррентное соотношение. Чем больше звёзд, тем меньше слагаемое 2n log**...* r, но тем больше km. Равновесие достигается при каком-то k. Но мы поступим грубее: превратим слагаемое n log**...* r в 2m. Перед этим финальным шагом вместо r везде подставим n — верхнюю границу на ранг исходного леса F (хотя по лемме 1 можно было бы положить r = log n, но не суть). Введём следующую функцию:

α(m,n) = min{k: n log**...* n < 2m, где число звёзд равно k}.

Функцию α(m,n) называют функцией обратной к функции Аккермана. Напомню, что мы интересуемся только случаем m ≥ n. По определению α(m,n) выражение n log**...* n, в котором α(m,n) звёзд, меньше 2m. Собственно, мы и ввели функцию α(m,n), чтобы получить такой эффект при минимуме звёзд. Может быть это сразу было не заметно, но только что мы доказали, что m операций Union-Find выполняются за O(m α(m,n)).

Тадам!

Немного про обратную функцию Аккермана

Если вы видели обратную функцию Аккермана раньше, то скорее всего определение было другим (более непонятным), но дающим в итоге асимптотически ту же функцию. Исходное определение Аккермана, которым пользуется Тарьян, лично мне не говорит об этой функции ничего (при этом для области, для которой сам Аккермана ввёл свою функцию, определение было естественным). Определение же, предложенное Зейделем и Шариром (и только что приведённое), вскрывает «тайный смысл» обратной Аккермана. Добавлю ещё, что, строго говоря, «функция обратная к функции Аккермана» — это неверное название, потому что α(m,n) — функция двух переменных и она никак не может быть «обратной» к какой-то функции. Поэтому иногда говорят, что α(m,n) — псевдообратная Аккермана. Саму функцию Аккермана я приводить не буду.

Теперь чуть-чуть анализа. Максимум α(m,n) достигается при m = n. Даже очень небольшие отклонения (например m ≥ n log***** n) делают α(m,n) константой. Функция α(n,n) растёт медленнее log**...* n для любого числа звёзд. Кстати, определение α(n,n) выглядит похожим на определение итерации:

α(n,n) = min{k: log**...* n < 2, где число звёзд равно k}.

Конечно, это не предел и есть функции, которые растут ещё медленнее, например log α(n,n). Удивительно другое: α(m,n) возникает при анализе столь естественного алгоритма. Ещё более удивительно, что есть доказательство того, что улучшить полученную оценку O(m α(m,n)) нельзя.