Нейронные сети не могут обобщать периодические зависимости. Как это исправить?
Данная статья состоит из двух частей:
Часть 1. Мой опыт применения периодической функции активации в нейронных сетях
Часть 2. Перевод некоторых, интересных выжимок из статьи.
Часть 1. Мой опыт применения периодической функции активации в нейронных сетях
Мотивация
Пока крутые ребята создают GigaChat, вернемся к базе.
Изучая нейронные сети, все глубже сталкиваешься с тем, что не ко всем задачам применимы полносвязные глубокие нейронные сети с классическими слоями Linear и слоями активации Relu, Sigmoid, Than и их вариации. Почему не используют остальные функции в качестве активации, например, периодические?
Периодические функции это естественный процесс.
В целом, периодические функции являются одной из самых основных функций, важных для человеческого общества и естествознания: суточные и годовые циклы в мире диктуются периодическими движениями солнечной системы.
Человеческому организму присущи биологические часы, которые носят периодический характер, количество пассажиров в метро меняется ежедневно, а фондовый рынок, курс биткоина это все в своем роде периодические последовательности.
Мировая экономика также следует сложным и накладывающимся друг на друга циклам разных периодов, интересный видеоролик на эту тему есть у Ray Dalio.

Во многих научных сценариях мы хотим смоделировать периодическую систему, чтобы иметь возможность предсказать будущую эволюцию, основываясь на текущих и прошлых наблюдениях. В то время как глубокие нейронные сети являются отличными инструментами для апроксимации. Можно сказать с натяжкой, что они «интерполируют» между существующими данными. Поэтому их реализация плохо подходит для экстраполяции, то есть они не могут обобщить зависимость, особенно периодическую, на известном распределении данных и применить те же правила, патерны в тех местах, где нет обучающих данных.
Если мы заранее знаем, что задача является периодической, мы можем легко решить ее с помощью пребразования Фурье. Однако во многих ситуациях мы априори не знаем, является ли проблема линейно угловой (Relu), периодической или содержит периодический компонент. В таких случаях важно иметь универсальную модель, которая была бы достаточно гибкой для моделирования как периодических, так и непериодических функций.
Расмотрим теоретическую часть, на простых функциях
Применение стандартных подходов
Сгенерируем тренировочные и валидационные данные тривальных функций
y=x, y=sin(x), y=tahn(x), y=x^2
Диапазон train data x=[-20;-4] and [4:20]
Пробел (отсутствие данных) в train data x [-4;4] поможет иследовать способность сети к интерполяции
Диапазон valid data x=[-60;60] валидационная data взята так чтоб посмотреть как себя поведет нейронная сеть на тех диапазонах, где обучающих данных в принципе нет, с помощью этого иследуем эксторпаляцию.
Code gen data:
import torch
import matplotlib.pyplot as plt
import matplotlib
class Gen_data:
def __init__ (self, func, ydown_scale, yup_scale ):
# Data for train
x_train = torch.rand(700)
x_train = x_train * 40.0 - 20.0
self.x_train = x_train[ (x_train <= -4) | (x_train >= 4) ]
self.y_train = func(self.x_train)
# Validate data
self.x_val = torch.linspace(-60, 60, 600)
self.y_val = func(self.x_val)
# For correct view plottig data
self.ydown_scale = ydown_scale
self.yup_scale = yup_scale
def get_train_unsqueeze(self):
return torch.unsqueeze(self.x_train, 1), torch.unsqueeze(self.y_train, 1)
def get_val_unsqueeze(self):
return torch.unsqueeze(self.x_val, 1), torch.unsqueeze(self.y_val, 1)
def plot_initdata(data):
# generate data
x_train = data.x_train
y_train = data.y_train
x_val = data.x_val
y_val = data.y_val
# Plot data
plt.scatter(x_train.numpy(), y_train.numpy(), s=20, color = "purple", label='Train data')
plt.plot(x_val,y_val, 'b-', label='Valid data')
plt.title('$y = x$');
plt.legend(loc='upper left')
plt.xlabel('$x$')
plt.ylabel('$y$')
Сами графики:
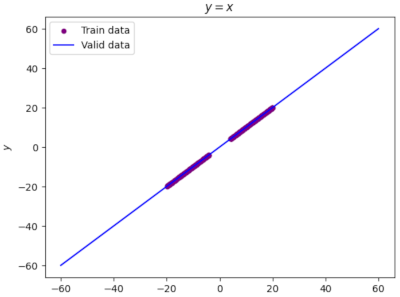
code y=x
# Define function
line_func=torch.clone
line_data=Gen_data(line_func, -65,65)
plot_initdata(line_data)
график y=x
code y=sin (x)
matplotlib.rcParams['figure.figsize'] = (30.0, 5.0)
sin_data = Gen_data(torch.sin, -4,4)
plot_initdata(sin_data)
график y=sin (x)

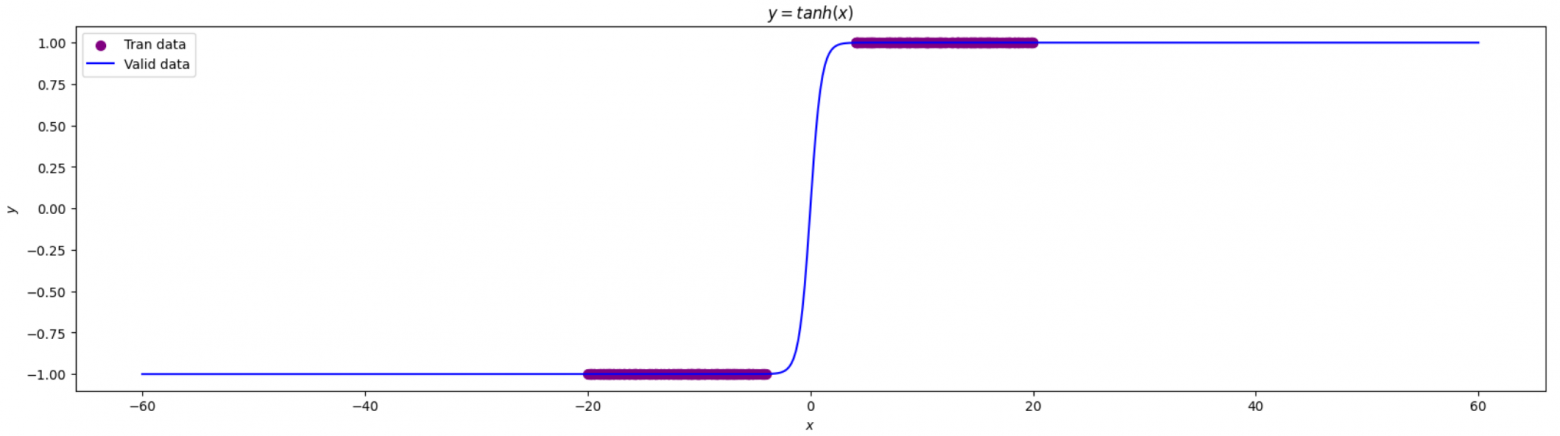
code y=tahn (x)
matplotlib.rcParams['figure.figsize'] = (20.0, 5.0)
tanh_data = Gen_data(torch.tanh, -2,2)
plot_initdata(tanh_data)
график y=tahn (x)
code y=x**2
matplotlib.rcParams['figure.figsize'] = (20.0, 10.0)
# Define function
def parabola(x_input):
return torch.pow(x_input, 2)
parb_data = Gen_data(parabola,-20,400)
plot_initdata(parb_data)
график y=(x)**2

Создадим нейронную сеть
Создадим однослойную полносвязную нейронную сеть с 1 скрытым слоем из 512 нейронов и активационным слоем Relu
code pytorch Net
import torch.nn as nn
import torch
class Net(torch.nn.Module):
def __init__(self, n_hidden_neurons):
super().__init__()
# YOUR CODE HERE
self.fc1 = nn.Linear(1, n_hidden_neurons)
self.act_relu = nn.ReLU()
self.fc2 = nn.Linear(n_hidden_neurons, 1)
pass
def forward(self, x):
x = self.fc1(x)
x = self.act_relu(x)
x = self.fc2(x)
return x
def loss(pred, target):
squares = (pred - target)**2
return squares.mean()
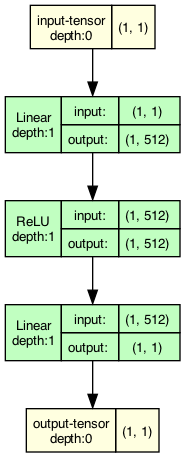
Будем тренировать данную сеть на наших заготовленных данных:
Результат на функции y=x
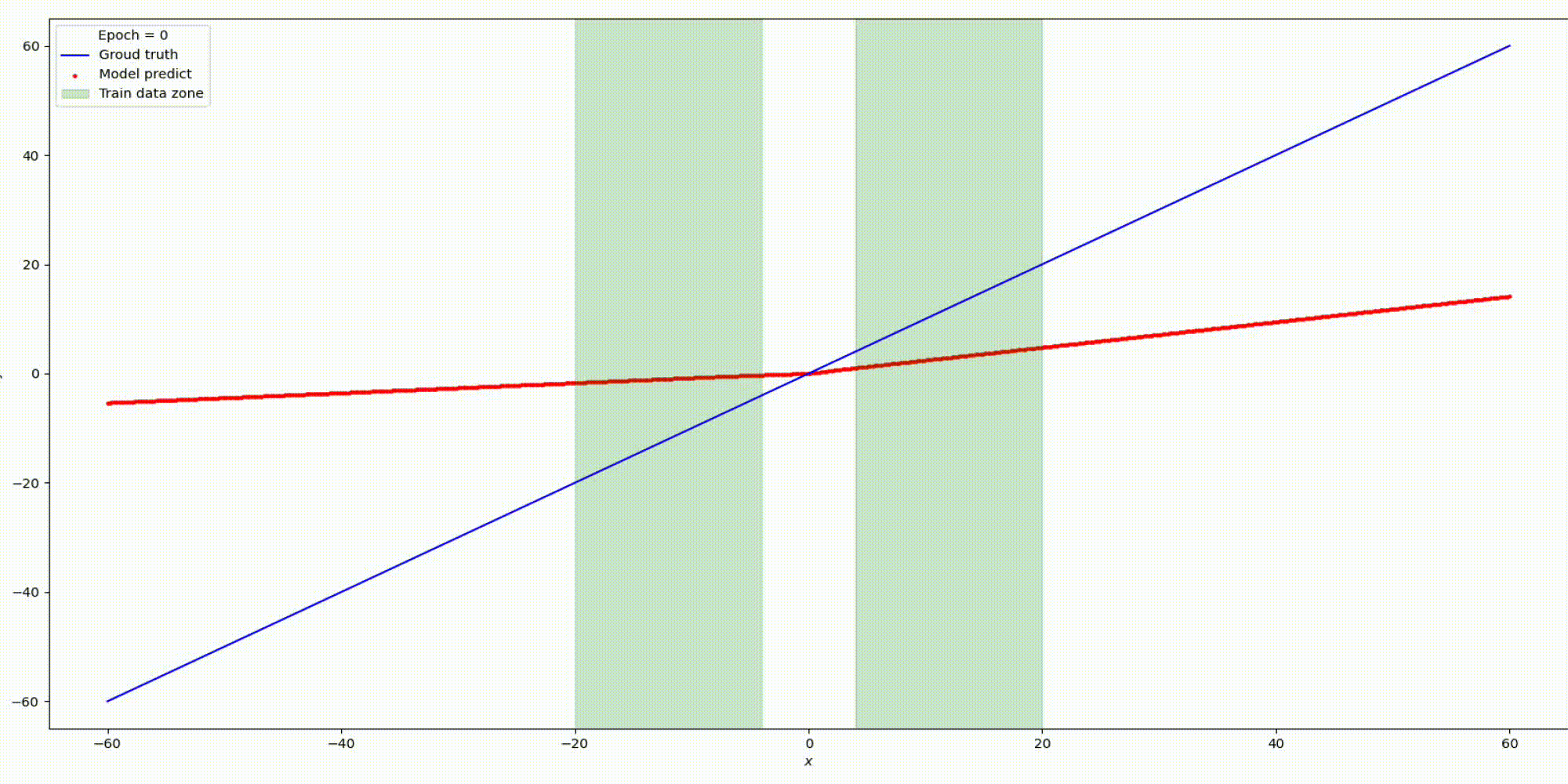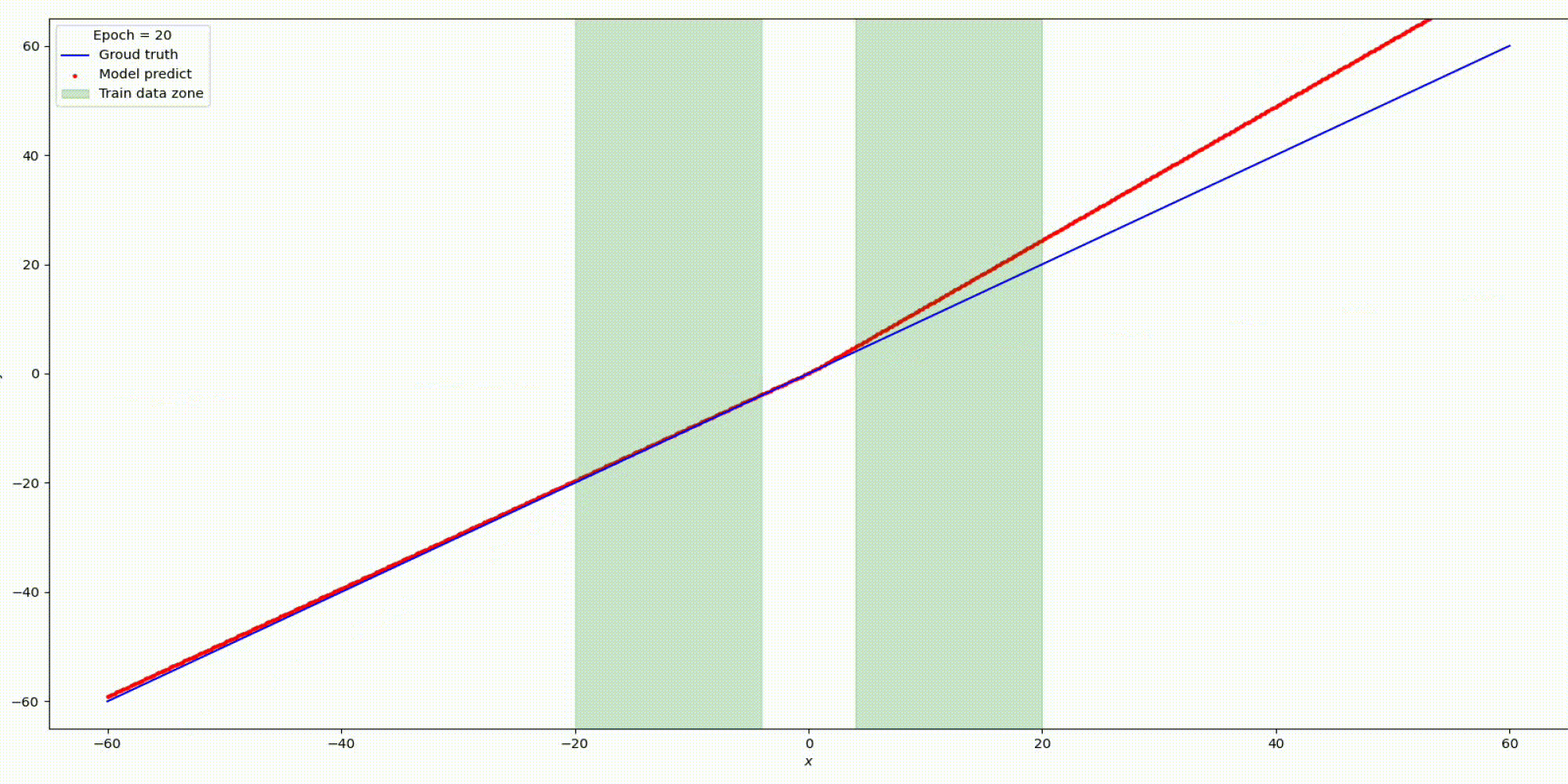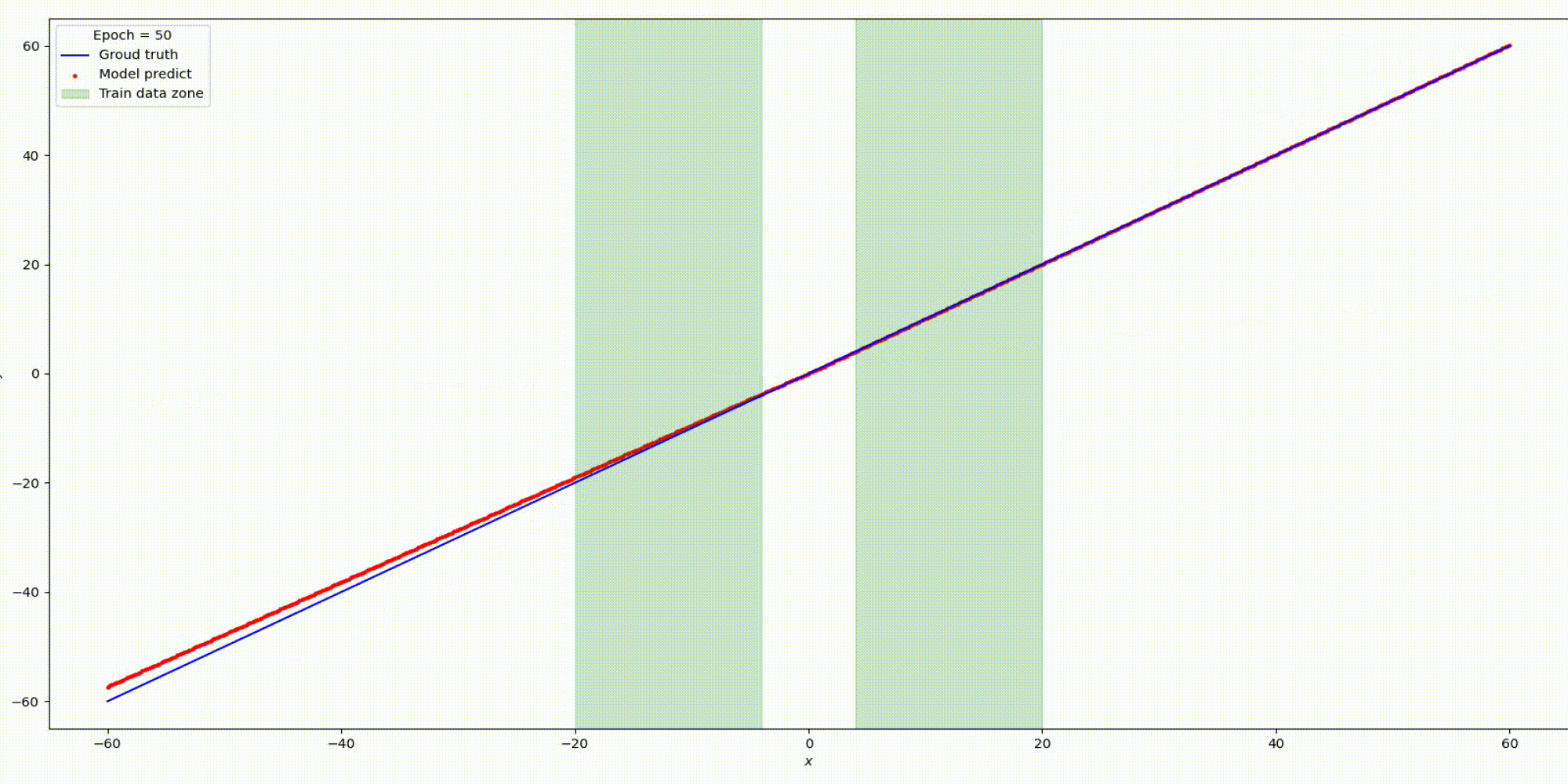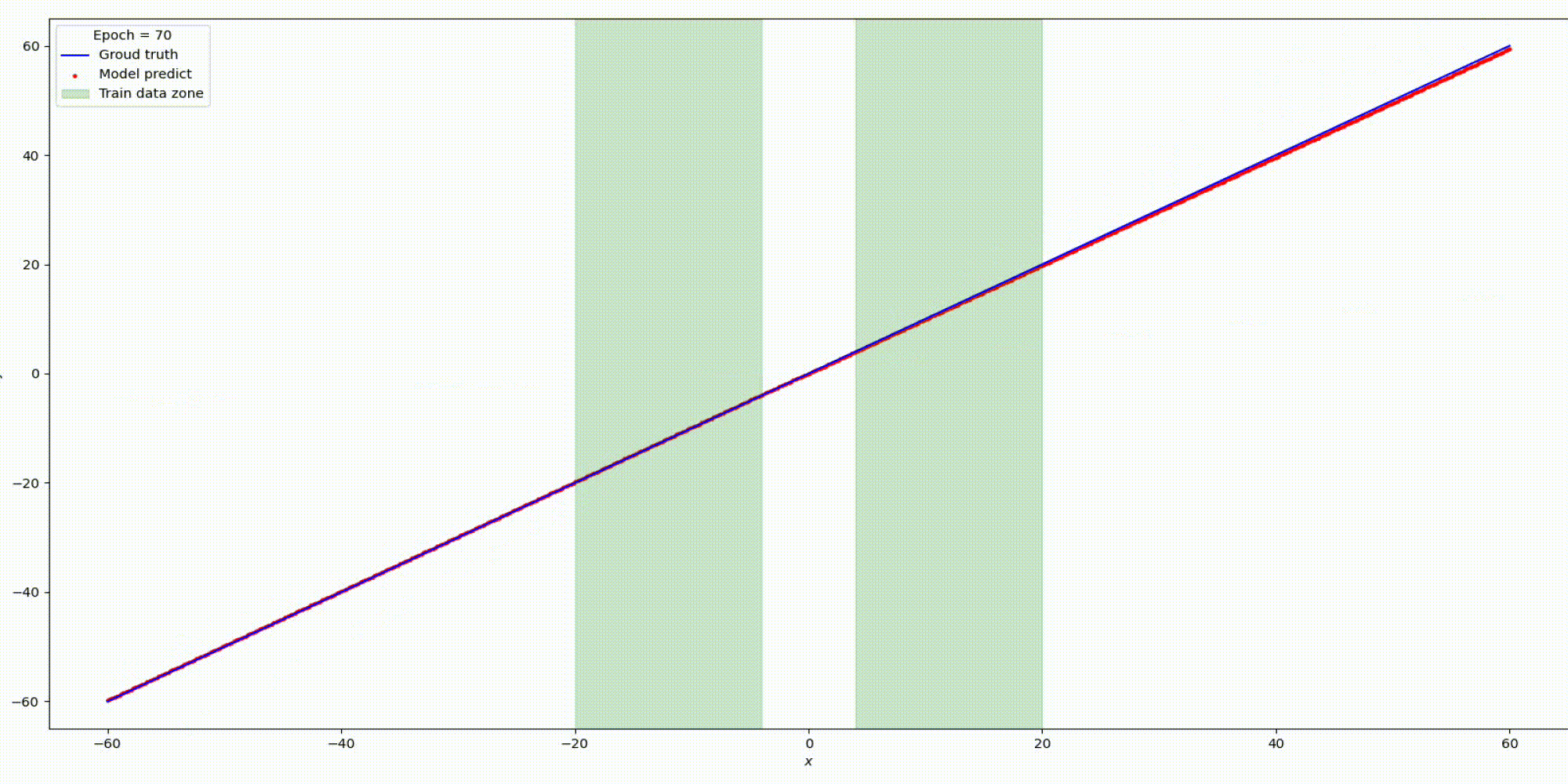

Результат на функции y=sin (x)


Результат на функции y=tanh (x)
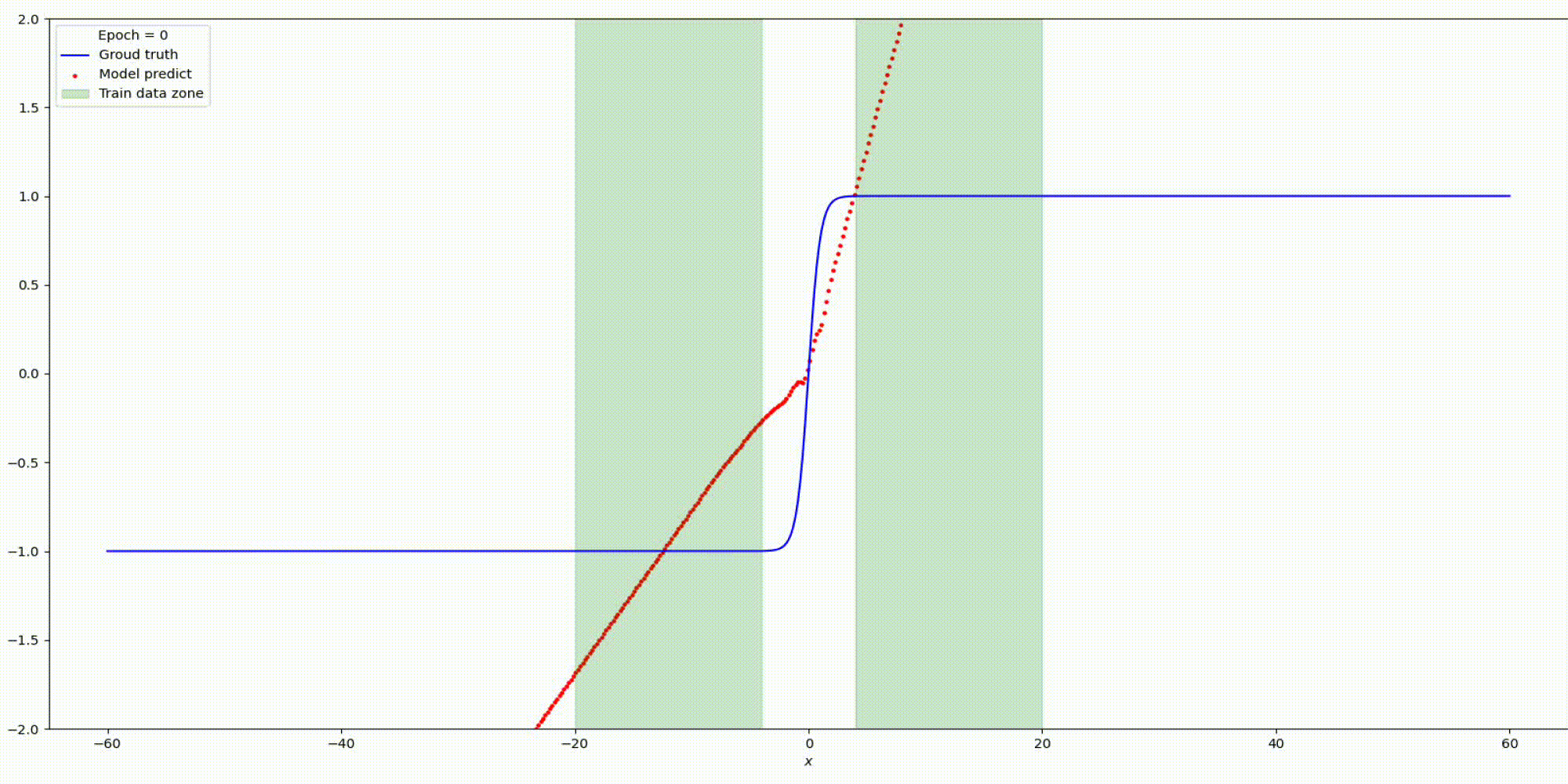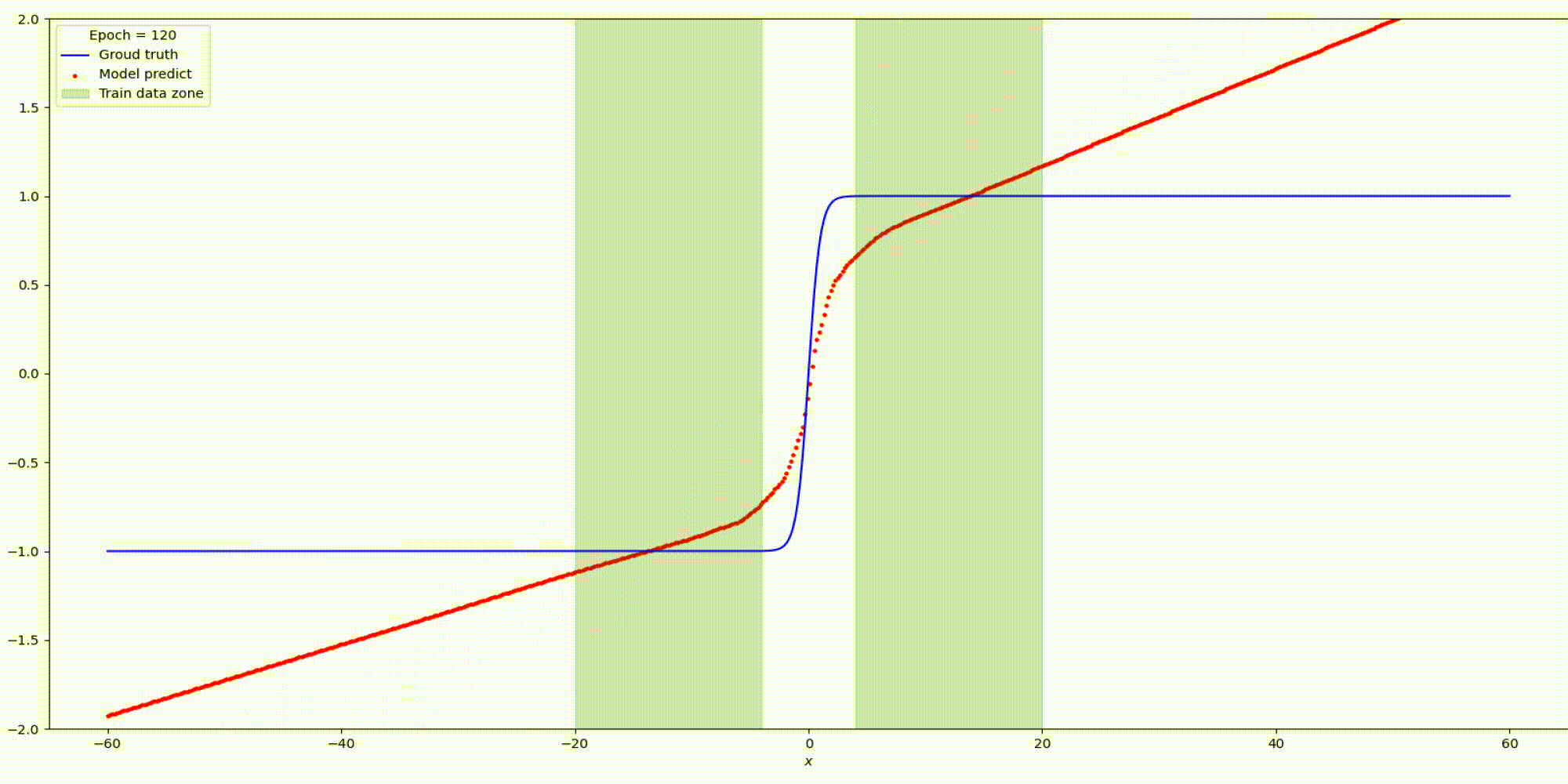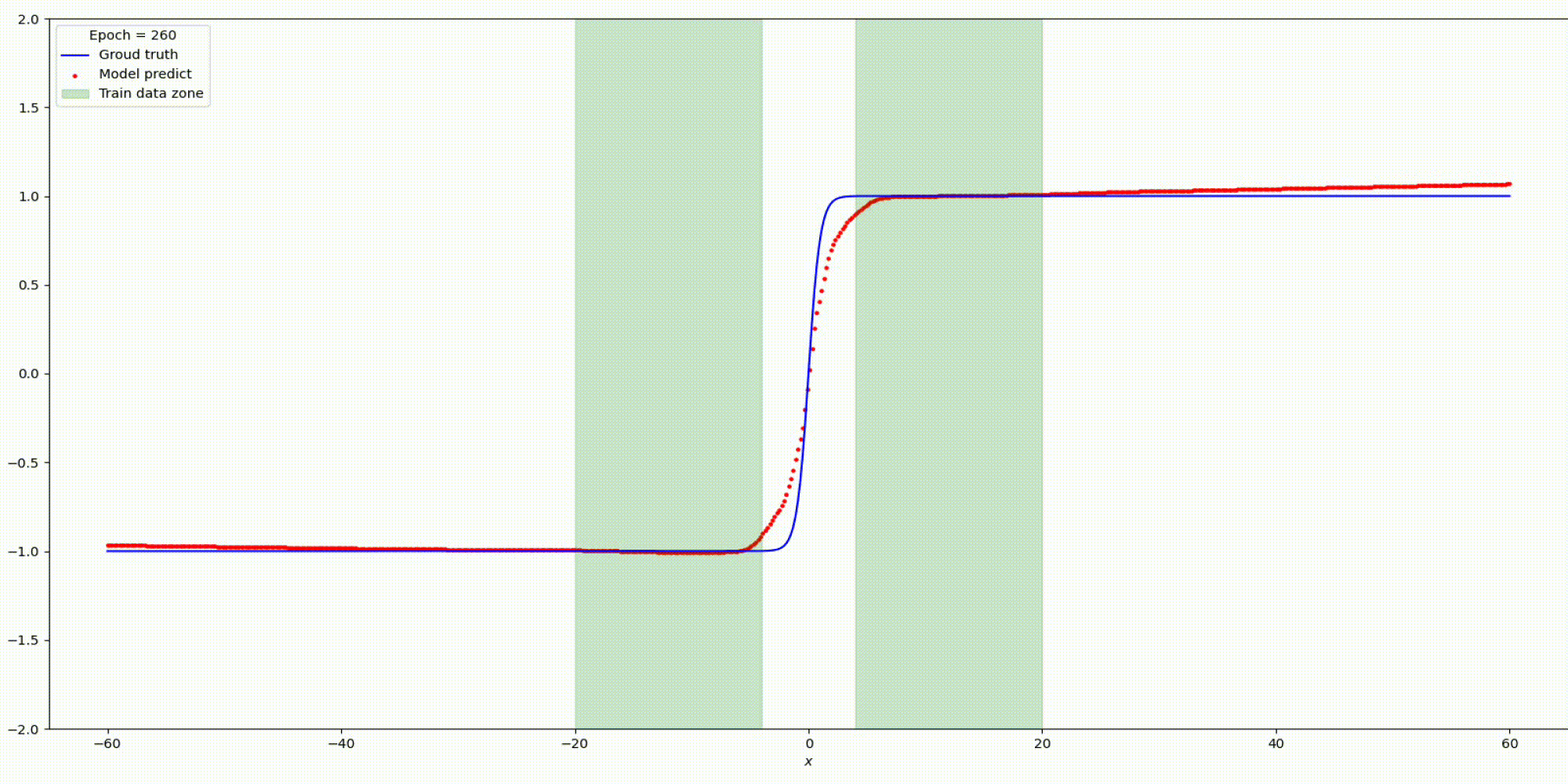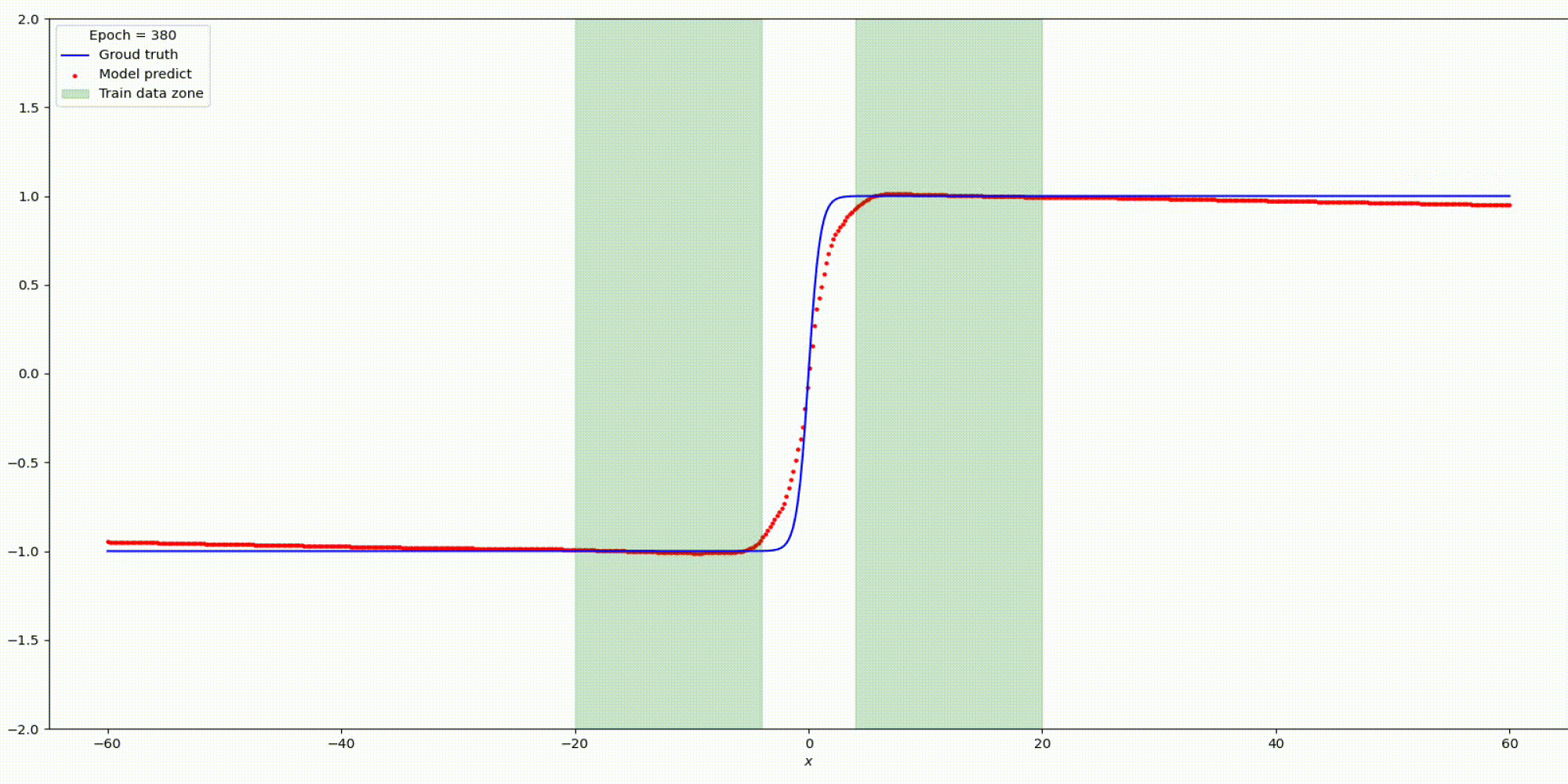
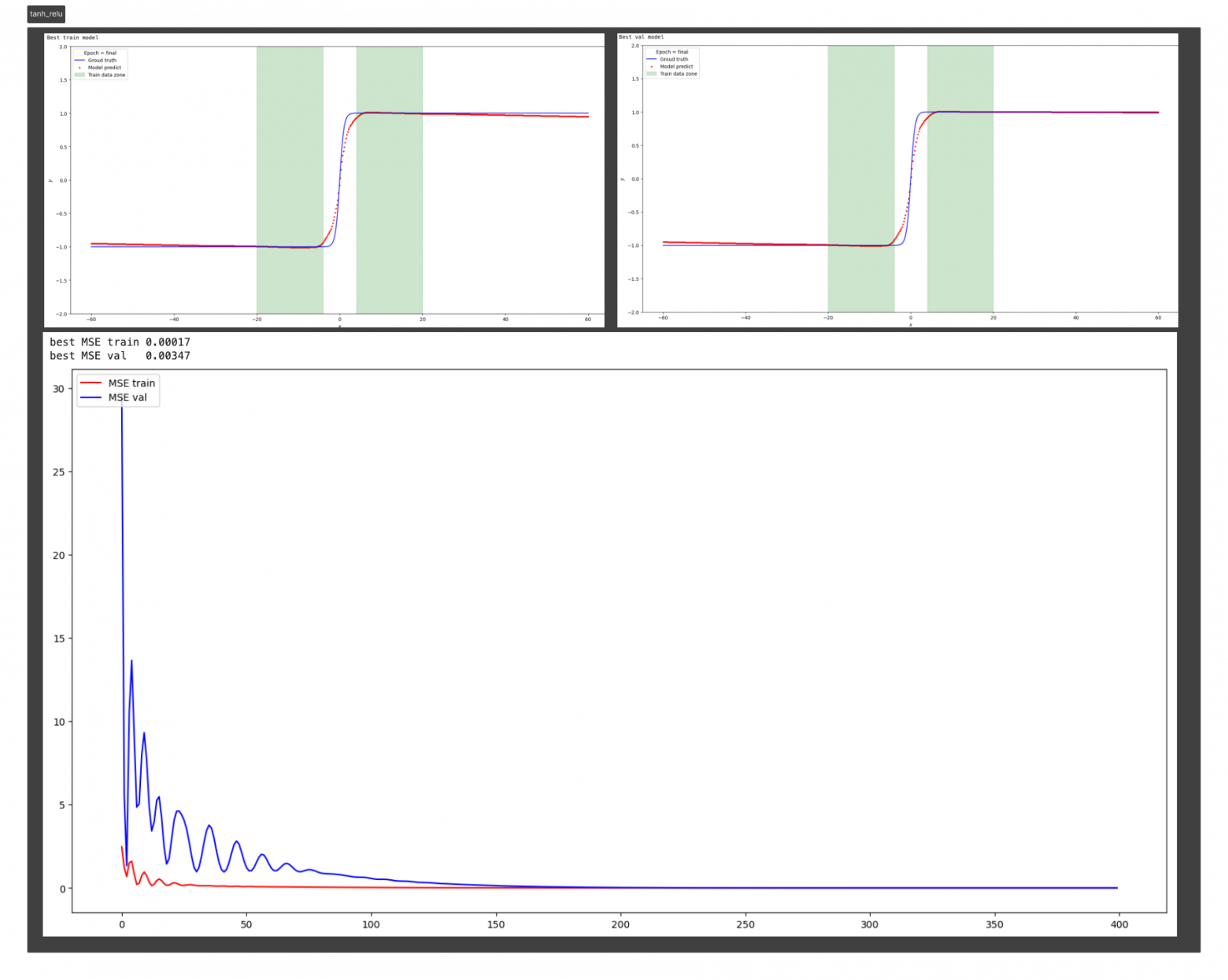
Результат на функции y=parab (x)


Существуют некоторые предыдущие методы, предлагающие использовать функции периодической активации (Fourier neural networks). В данном подходе предлагается использовать периодические функции, sin (x) и cos (x), или их линейные комбинации в качестве функций активации. Однако такие функции активации очень трудно оптимизировать из-за большого вырождения локальных минимумов и экспериментальные результаты показывают, что использование sin в качестве функции активации работает плохо, за исключением очень простых моделей и что оно не может конкурировать с функциями активации на основе ReLU в стандартных задача.
Для начала вспомним как выглядит функция активации Relu:

Теорема:
Рассматривая сети с прямой связью f (relu (x)) с произвольной, но фиксированной глубиной и шириной d_1, … d_h+1
где z есть вещественный скаляр, u — любой единичный вектор размерности d1, а Wu ∈ Rd1×dh — постоянная матрица, зависящая только от u.

Приведенная выше теорема гласит, что любая полносвязная нейронная сеть с активацией ReLU сходится к линейному преобразованию W*u в асимптотическом пределе и это экстраполированное линейное преобразование зависит только от u. Смотрите иллюстрацию. (Не самый удачный перевод через Google Translate)
Также мы имеем понимание, что такая простая однослойная нейронная сеть Linear + Relu, при достаточном количестве нейронов, может апроксимировать с любой точностью, любую последовательность данных.
На основании предыдущих экспериментов с простыми функциями можно сделать вывод: выбор функций активации играет решающую роль интерполяционных и экстраполяционных способностях нейронных сетей и такие свойства интерполяции и экстраполяции, в свою очередь, влияют на обобщающие способности сети.
Мотивация выбора периодичной функции активации.
На ум сразу приходит взять в качестве активационной функции y=sin (x) или y=cos (x).

Однако проблема этих функций заключается не в их способности к обобщению, а в их оптимизации. На самом деле, sin не является монотонной функцией. Использование sin в качестве функции активации создает бесконечно много локальных минимумов в решениях (поскольку сдвиг «значения активации» на 2π дает та же функция), что затрудняет оптимизацию sin (x).
То есть нам нужна какая-то модифицированная sin (x), например, наклонная функция, с каким-то обучающимся параметром.
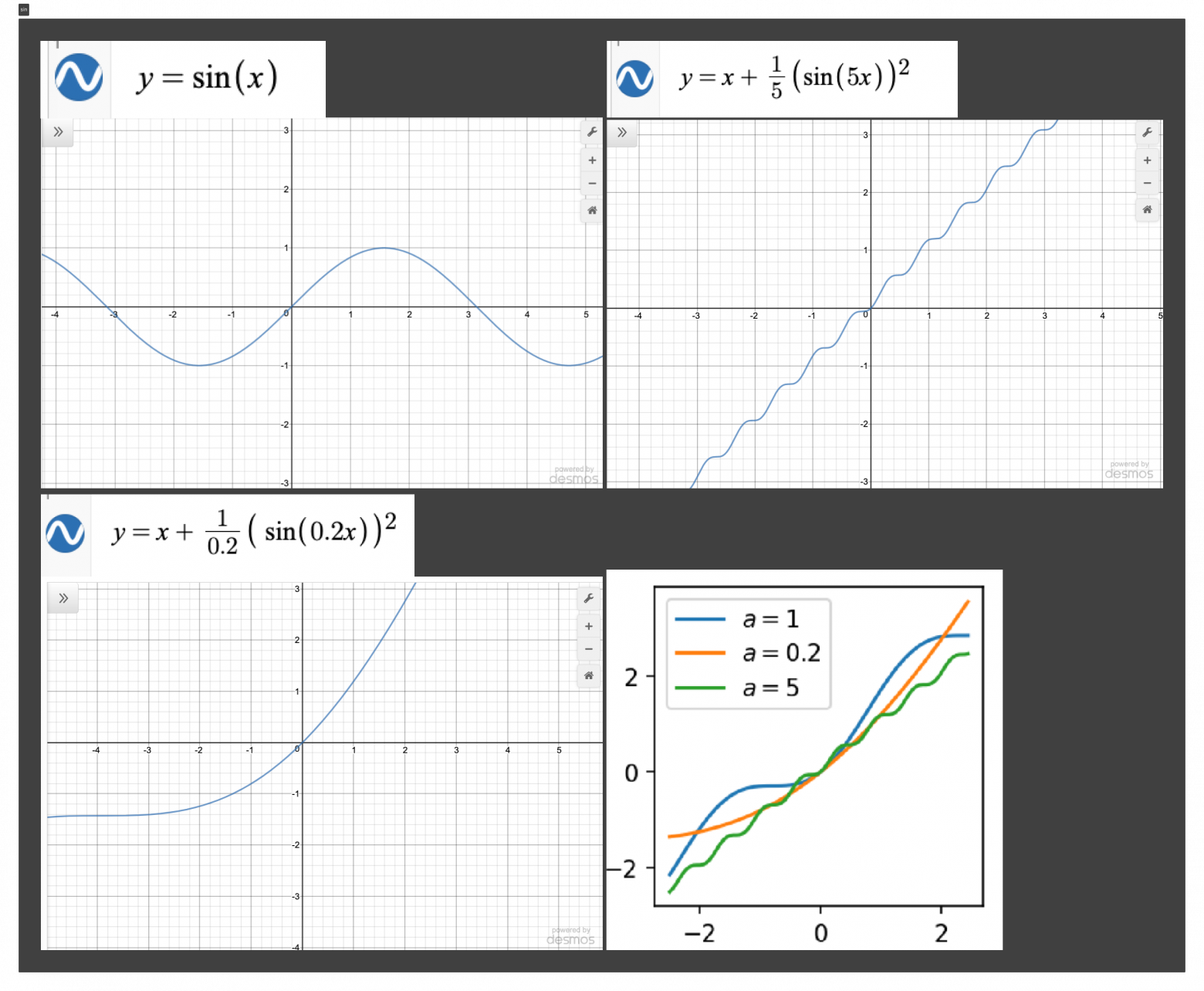
Реализацию данной функции в PyTorch позаимствовал в репозитории EdwardDixon.
