На пути к индивидуальному образованию: анализ данных Яндекс.Репетитора25.06.2020 10:17

vymo7so17xlldmfy42q2ccpg-d4.png

Наверняка почти каждый мечтает о персонализированном образовании: двигаться к своей образовательной цели максимально коротким путём, решать только те задачи, состав и сложность которых подстраиваются под тебя, с пользой проводить любой отрезок времени независимо от длительности и структуры. Неважно, будь то пятиминутный перерыв от работы или ежевечерние занятия на протяжении месяцев.

Такой инструмент позволил бы экономить огромное количество времени и при этом добиваться значительно лучших результатов. Эффективность обмена знаниями значительно повысилась бы, а вслед за этим ускорился бы и прогресс.

Но пока человечество совершает лишь робкие попытки подобраться к пониманию, как создавать такой инструмент. Свою попытку осуществила и команда Яндекс.Репетитора. Сервис, запущенный менее двух лет назад, накопил данные о ста миллионах решений различных задач, и этого достаточно для интересной аналитики. Понятно, что образование состоит не только из задач, но сегодня мы сфокусируемся на них.

В статье я расскажу, какую аналитику мы научились строить на базе собранных данных и благодаря каким свойствам сервиса она оказывается возможной. В самом конце вас ждёт небольшой отчёт о нашей первой попытке построить сервис для персонализированного образования и о результатах этого эксперимента.


1. Почему персонализированное образование — это сложно

Построение современной персонализованной образовательной системы — сложная задача. С точки зрения специалиста по анализу данных ситуация выглядит так:


  • Образовательные процессы предполагают чрезвычайно длительный feedback loop: воздействие производим прямо сейчас (выдаём задачку пятикласснику), результат наблюдаем очень нескоро (поступит ли он в МГУ, заработает ли миллион?). Это ограничивает число доступных наблюдений, затрудняет эксперименты и неблагоприятно сказывается на актуальности моделей: современным пятиклассникам нужно не то же самое, что пятиклассникам пять лет назад.
  • Образовательные данные очень шумные, их мало, к тому же они нерепрезентативны. Результаты обусловлены огромным числом ненаблюдаемых факторов (исторический момент, социальная среда, семья, друзья, дополнительные и самостоятельные занятия…) и доступны, как правило, только для небольших и очень разрозненных групп людей.
  • Exploration ограничен: чтобы получить данные для обучения моделей, нельзя обязать миллионы людей использовать случайные или просто существенно субоптимальные образовательные стратегии.
  • Объём доступного образовательного контента, который подходит для глубокой персонализации, незначителен. В лучшем случае контент производится с прицелом на несколько крупных и очевидных пользовательских групп. Например, это могут быть материалы курсов по ML для трёх типов людей:
    — без математического образования,
    — с математическим образованием и при этом новичков в ML,
    — для людей, уже глубоко погруженных в ту или иную область.

    На такой базе сложно строить хорошие персональные модели, так как выбор будет в большей степени обусловлен качеством материала, а не персональными свойствами студента. Я думаю, этот недостаток можно будет преодолеть, если появится работающий рынок образовательных материалов, который сможет проактивно предлагать лучшим авторам создавать контент, востребованный в узких группах пользователей.


2. Яндекс.Репетитор

Список выше можно продолжать, но перечисленные в нём проблемы поддаются решению. На мой взгляд, хороший план может выглядеть так:


  1. Рассматриваем одну очень простую задачу с коротким feedback loop, решение которой при этом будет востребовано широкими массами пользователей. Например, такой задачей может быть подготовка к выпускным школьным экзаменам: всякий школьник очень хочет получше сдать ОГЭ и ЕГЭ. Скорость фидбэка обеспечим так: индивидуальным событием будет успешность или неуспешность решения очередной предложенной задачи. Тестовый характер большинства заданий снимает сложности с анализом успешности решений.
  2. Создаваемый сервис должен быть популярен, чтобы покрыть максимально возможное количество пользователей. При этом он должен качественно логировать все события, чтобы в дальнейшем можно было учитывать их при создании моделей.
  3. Вместо того чтобы осуществлять честный exploration, можно просто сравнивать разные стратегии подбора заданий для пользователей. Если в их показателях будут статистически значимые различия — вероятно, в будущем мы справимся с построением оптимальных стратегий.
  4. Тогда единицей контента будет являться конкретная задача. За годы создано создано огромное количество задач в области ОГЭ и ЕГЭ, и построение персональных наборов задач кажется очень содержательной работой. Ясно, что у всех разный уровень подготовки, и можно было бы строить рекомендации, исходя из сильных и слабых сторон каждого конкретного школьника.
  5. Когда работоспособность методов и моделей будет показана на примере задачи подготовки к ЕГЭ, мы сможем намного смелее подступаться и к другим дисциплинам, постепенно расширяя границы применимости рекомендательных моделей.

Исходя из таких рассуждений и появился сервис Яндекс.Репетитор. Это, в общем-то, большой задачник для школьников, готовящихся к ЕГЭ или ОГЭ. Школьные задачи можно решать по отдельности или в составе вариантов. Конечно, можно и просто смотреть разборы или оставлять задачи без ответов. При анализе такие случаи потребуется отбрасывать.

Мы сделали блок рекомендованных задач. Предположим, школьник попадает на страницу предмета и для него собрана статистика — достаточный объём решений заданий этого предмета. Каждый такой школьник может увидеть следующий блок:

0eisl4gcmdayhk06oakfwrr6jgu.png
Ссылка на этот блок

В нём демонстрируются задания, подбираемые разными вариантами алгоритмов.


3. Простейшая аналитика

Первая группа наблюдений лежит на поверхности: можно изучать пользовательский интерес к образованию в зависимости от дня недели, времени года, времени суток и т. д.

Вряд ли кто-нибудь удивится, что максимально активные образовательные дни — это дни с понедельника по четверг. Пятница и воскресенье примерно равны, а по субботам наблюдается значительное снижение активности. На сглаженном годовом графике видно, что школьники не проявляют интереса летом, в Новый год и во время других праздников, на каникулах.

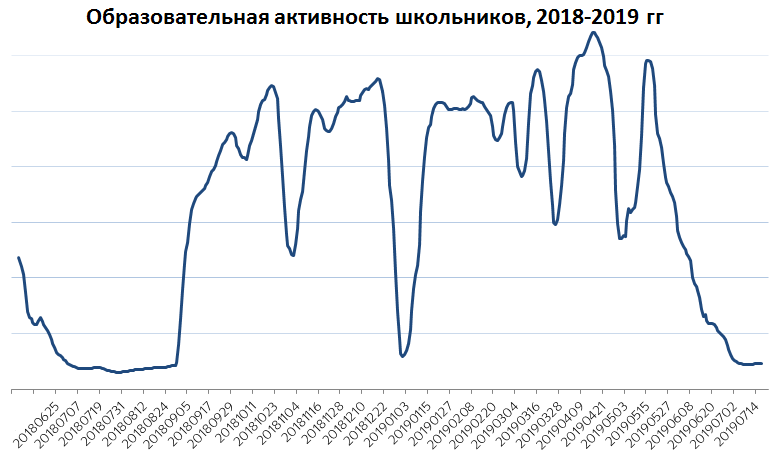
wwj-zdx9xctd7b5rmhinx8b5dde.png
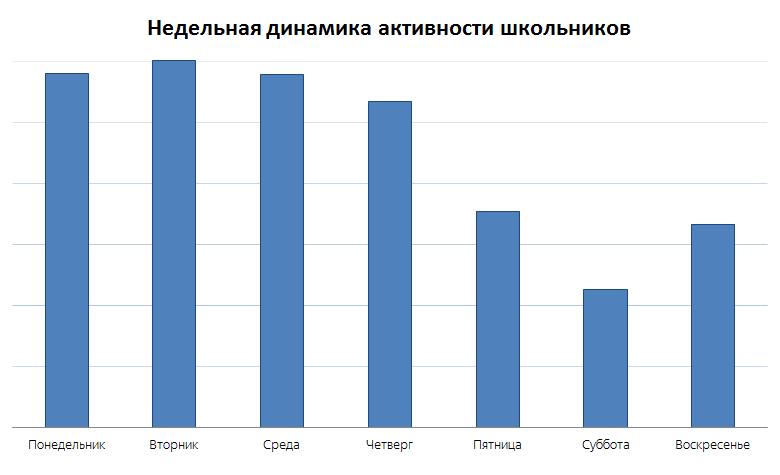
dhy_xxv9xtldggkzav3upq8snpu.png

Но это всё лежит на поверхности и даже не требует создания нового сервиса — хватило бы и анализа данных веб-поиска.


4. Бесконтекстные модели сложности

В простейшем случае показателем сложности задачи может служить средняя успешность её решений: задача, где верными оказались 40% ответов, почти наверняка сложнее задачи, где тот же показатель составляет 60%.

Но такой анализ слишком прост и не учитывает разного уровня подготовки пользователей. Простой пример: задачи тестовой части ЕГЭ по математике профильного уровня решаются в среднем существенно успешнее задач базового уровня. Конечно, из этого нельзя делать вывод, что задачи профильного уровня легче. Просто их решают более подготовленные школьники, для которых сложность не в задачах тестовой части.

Поэтому потребуется более комплексная модель. Первой рассмотрим рейтинговую модель, которую уже давно придумали в шахматах, адаптировали к олимпиадному программированию, баскетболу и многим другим областям.

Введём обозначения:


  • $U=\{u_1,u_2,...,u_n\}$ — множество пользователей;
  • $T=\{t_1,t_2,...,t_m\}$ — множество задач;
  • $X=\{x_1,x_2,...,x_N\}$, где $x_k = (u_{i_k}, t_{j_k}, a_k)$, — множество решений.

Каждая тройка $(u_{i_k}, t_{j_k}, a_k)$ из множества $X$ трактуется так, что пользователь $u_{i_k}$ решал задачу $t_{j_k}$ и дал верный ответ, если $r_k = 1$ и неверный, если $a_k = 0$.

Сопоставим каждому пользователю и каждой задаче рейтинг — некоторое вещественное число. Точнее, определим функцию $r:U \cup T \rightarrow \mathbb{R}$, значения которой и будем называть рейтингами. Скажем, что разница рейтингов пользователя и задачи должна предсказывать вероятность верного решения:

$P_r(a_k = 1) = \frac{1}{1 + \exp\Big(r(t_{j_k}) - r(u_{i_k})\Big)}$

Обозначим через $P_r(x_k)$ вероятность верной классификации:

$P_r(x_k) = a_k \cdot P_r(a_k = 1) + (1 - a_k) \cdot \Big(1 - P_r(a_k = 1)\Big)$

Выбирать значения рейтингов будем простым методом максимального правдоподобия:

$r = \arg \max_{r' : U \cup T \rightarrow \mathbb{R}} \prod_{k=1}^{N}P_{r'}(x_k)$

Выглядит немного громозко, но в действительности всё просто: такие рейтинги легко строить при помощи стохастического градиентного спуска, совсем как при обучении логистической регрессии.

Конечно, можно строить отдельные рейтинги для пользователей в рамках различных тематик. Скажем, школьник может очень хорошо справляться со стереометрическими задачами и при этом плохо с задачами по теории вероятностей. Описанный метод вполне подходит и для этого.

Приведу пример результата вычисления рейтингов для отдельных номеров задач ЕГЭ по матетатике базового уровня и пользователей Яндекс.Репетитора. Чтобы он был насколько-то обозрим, я оставил только четыре группы задач: две самых сложных и две самых простых.

Я привожу три характеристики для каждой темы:


  • сложность — величину рейтинга этой темы;
  • долю верных решений — среди всех решений всех задач, относящихся к этой теме;
  • средний рейтинг пользователей, решавших задачи из этой темы.

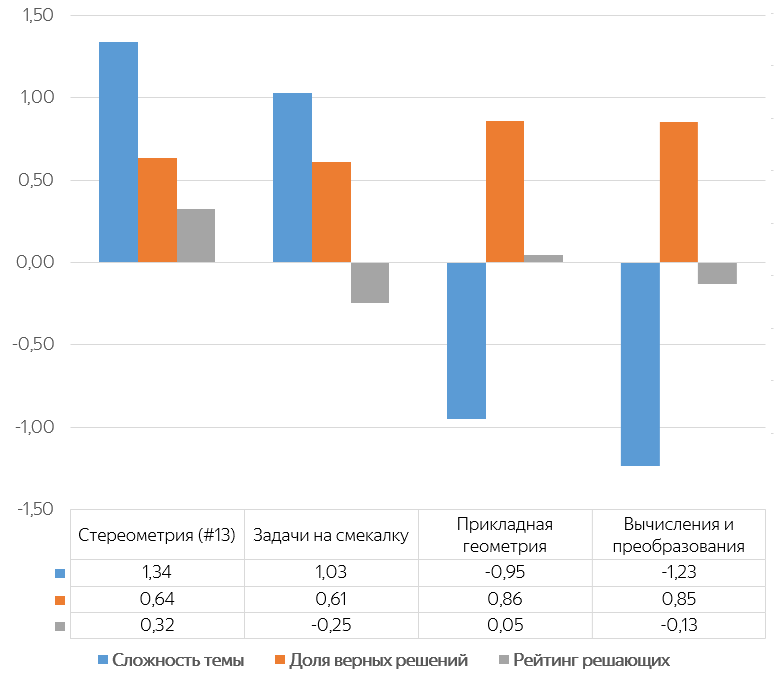
d7mxl5ujev-sl6avqe4i-rcyhb0.png

Например, в среднем стереометрические задачи решают верно чаще, чем задачи на смекалку (64% и 61% верных ответов соответственно), но именно стереометрия оказывается наиболее сложной темой. Причём задания в ней решают более сильные школьники: средний рейтинг пользователей, решающих задачи по стереометрии, оказался равен 0,32, тогда как задачи на смекалку решают пользователи со средним рейтингом -0,25. Таким образом, анализ сложности заданий требует анализа способностей пользователей, и это очень ценный вывод.

Понять, насколько рейтинги информативнее простой доли верных решений, позволяет следующее сравнение. Построим графики обеих величин, отсортировав темы по убыванию рейтинга:

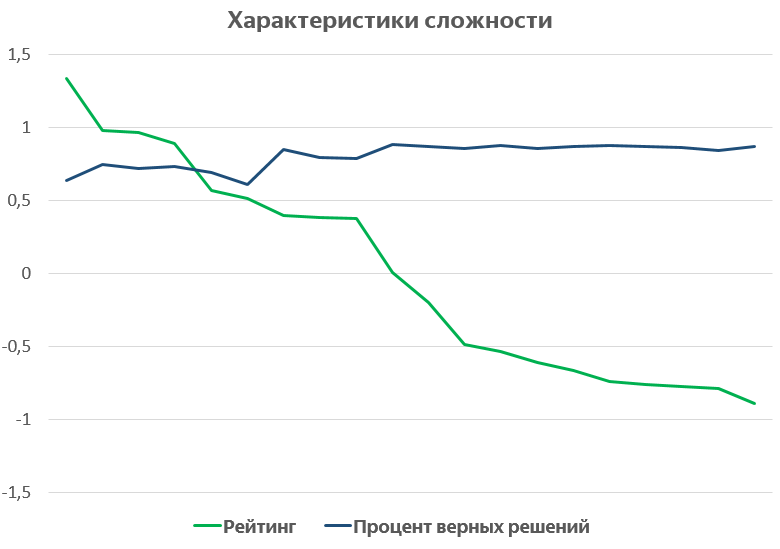
-1vvwhlzwmr0xvqlu6elqxcqkee.png

Хорошо видно, что с точки зрения доли верных ответов есть две группы задач: более сложные (70–75% верных решений) и более простые (85–90% верных решений). Рейтинги в этом смысле выглядят обеспечивающими больший разброс и большее разнообразие значений.

Последнее, на что очень интересно взглянуть: распределение рейтингов пользователей. Я построил вариационный ряд рейтингов пользователей и увидел такую картину:

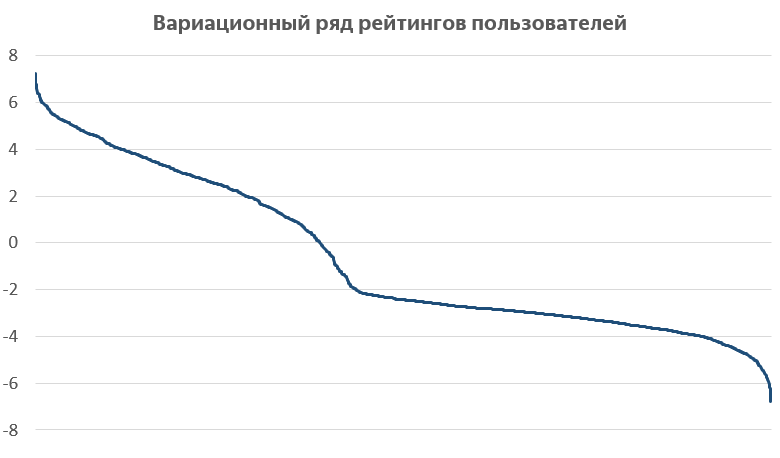
_qb4ajyb_o4pshbmf4_pouuhzqa.png

Этот график построен следующим образом. Для всех пользователей, решивших хотя бы десять задач на сервисе, построены рейтинги. Затем пользователи упорядочены по величине рейтинга, и по горизонтальной оси отложен номер пользователя в полученном рейтинге, а по вертикальной — величина самого рейтинга. Думаю, эта зависимость могла бы стать основой отдельного содержательного исследования.


5. Контекстные модели сложности

В предыдущем пункте я описывал, что происходит при определении рейтингов отдельных групп задач и пользователей. Естественное развитие этой идеи — использовать модели, зависящие от свойств задач и пользователей, а не бесконтекстные рейтинги.

Например, можно в качестве признаков использовать «слова» в условии задачи. К «словам» относятся не только cfvb слова, но и различные специальные термы, такие как математические символы и части формул.

Обучение будет производиться тем же методом максимизации правдоподобия, а модель для простоты используем линейную. То есть фактически будет обучена модель, которая умеет оценивать априорную сложность задачи по её тексту.

Если чуть формальнее, в терминах пункта 4 необходимо переопределить функцию рейтинга для задачи:

$r(t) = \sum_{term \in t} \omega(term)$

Здесь $\omega(term)$ — вес терма $term$. Эти веса будут оптимизироавться в процессе обучения.

Затем рейтинг задачи будет уже линейной функцией по термам, входящим в формулировку задачи. Модель сложности задач будет свободна от смещений, вызванных разными характеристиками пользователей: оптимизация весов этой модели производится одновременно с оптимизацией рейтингов пользователей.

Анализируя веса различных термов, можно понимать, какие части заданий вызывают у школьников сложности. Например, при обучении подобной модели для базовой математики получилась следующая картина:

m6zluiquwdoeqlytn1sluipir2o.png

То есть при прочих равных школьники прекрасно решают задачи с корнями и треугольниками, но вероятность успеха уменьшается, если задача требует знания логарифмов или пирамид.

Ещё интереснее добавлять в такие модели персональные свойства пользователей. Скажем, пользователи, склонные пропускать задачи (оставлять поле ответа пустым), в среднем добиваются результатов аж на треть реже других. Склонность решать варианты, напротив, является показателем качества: в среднем такие пользователи справляются с задачами на 37% успешнее.

Конечно, это не означает, что прорешивание вариантов — отличный способ подготовки (впрочем, здорово, что более упорные школьники чаще добиваются успеха). Текущий уровень анализа не позволяет определять, какие из зависимостей отражают объективные причинно-следственные связи. Есть и хорошие новости: ясно, что нужно поменять в сервисе, чтобы это стало возможным.


6. Рекомендации

Я хочу, чтобы развитие идей из пунктов 4 и 5 привело к созданию модели, которая бы хорошо предсказывала полезность действий на сервисе (в том числе — полезность решения тех или иных задач).

В первом приближении такую модель можно вывести из любой модели сложности задач, использовав побольше персональных факторов пользователей. Тогда можно будет вычислить ожидаемую успешность в решении задач экзамена до и после решения той или иной задачи (с учётом вероятности её успешного решения). Этот метод выглядит реализуемым, необходимо лишь собрать побольше данных и аккуратно учесть каждый bias в них. Кроме того, для демонстрации работоспособности модели потребуется эксперимент, поставленный корректно, с соблюдением всех требований double blind studies.

Сейчас я не могу похвастаться всем этим, зато могу поделиться первыми результатами, дающими надежду на итоговый успех.

Для начала посмотрим на график априорной сложности самостоятельно решаемых задач. По горизонтали — номер задачи, которую решает пользователь (например, это 100-я задача, которую он решает на сервисе), по вертикали — сложность в простейшем её понимании: какая доля всех решений этой задачи является успешной.

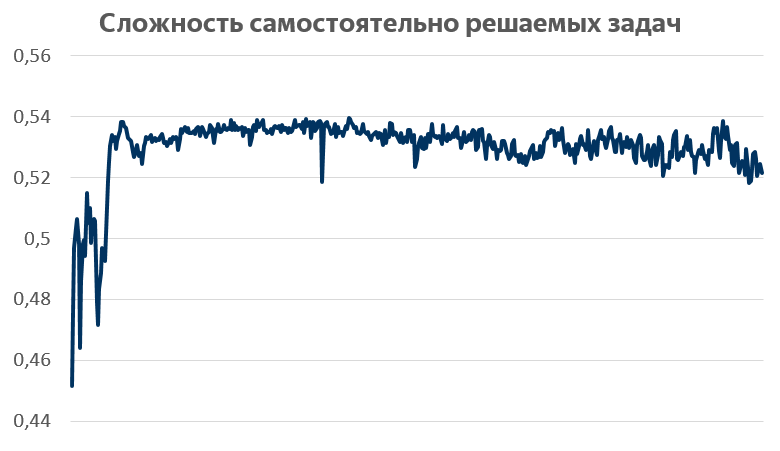
6pyhxegpkw-vdsxn6t31br2qohq.png

Здесь видны две важные проблемы самостоятельной подготовки. Первая: школьники решают задачи одной и той же сложности. Вторая: они решают слишком сложные задачи, с априорной вероятностью успеха всего 50%.

Мы на сервисе реализовали две стратегии рекомендации задач пользователям. Первая выдаёт случайные задачи, другая генерирует их неким относительно умным образом. На картинке ниже — динамика сложности предлагаемых задач в зависимости от номера.

Синяя линия показывает предсказание априорной вероятности решить задачу, зелёная — предсказание персональной вероятности решения (априорная не зависит от пользователя, персональная — зависит).

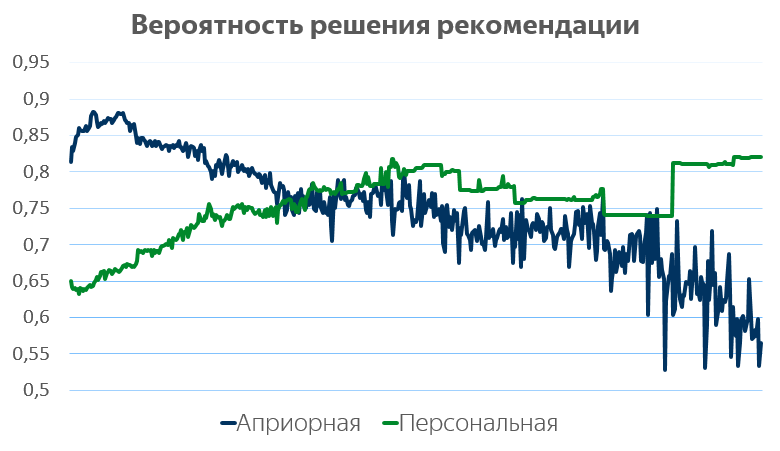
gc-33c2cluotsx6mr1xiw_fweh8.png

Хорошо видно, что поначалу мы предлагаем достаточно простые задачи, которые решаются с вероятностью 80–90%. Затем сложность постепенно нарастает, так что после нескольких сотен решённых задач их априорная вероятность решения снижается до 50%. Одновременно вероятность, что пользователь решит рекомендованную ему задачу, вырастает с 65% почти до 80%. Таким образом, пользователи наших «умных» рекомендаций всё лучше решают всё более сложные задачи!

Здесь я обязан сделать методологическое замечание: сказанное не доказывает, что наши рекомандации являются причиной роста успешности пользователей. Для такого вывода нужно провести корректное A/Б-тестирование. Например, возможен такой случай: более успешные школьники решают большее количество рекомендованных задач и график показывает только это, хотя при построении персональной модели сложности применялись различные методы для минимизации этого смещения. Тем не менее, приведённый график оставляет возможность того, что причиной являются именно рекомендации.

Есть, впрочем, один факт, который можно установить со всей определённостью. Оказывается, управляя только набором рекомендуемых задач (не меняя расположение блока рекомендаций, его визуальное представление или набор пользователей), можно статистически значимо влиять на количество решаемых задач.

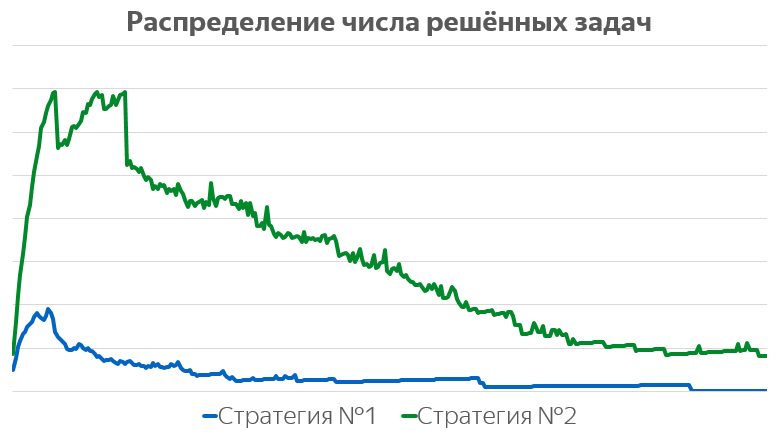
nabxcg_aygmwifkgmospoem8fvk.png

Эти графики устроены так: по горизонтали — число решённых рекомендованных задач, по вертикали — число пользователей, решивших не менее выбранного числа рекомендованных задач.

Хорошо видно, что «умные» рекомендации намного сильнее вовлекают пользователей. Некоторые особенности графиков вызваны тем, что на сервисе рекомендации выдаются блоками — по несколько десятков задач в день.


Что дальше

В статье я попытался показать, какого рода данные можно собирать, анализировать и использовать во благо общества при помощи сервисов, подобных Яндекс.Репетитору.

Очевидно, это не исчерпывающий набор возможных применений. Самое простое, что приходит на ум: анализ ошибочных ответов в задачах, определение причин ошибок и дальнейшее использование полученного знания в образовательном процессе. Стоило бы также поискать зависимости между темами. Скажем, школьник, плохо справляющийся с дробями, вряд ли преуспеет в решении задач по теории вероятностей. Думаю, неравнодушные читатели смогут придумать множество приложений, которые я даже не упоминал в статье.

Мы продолжим работать в этом направлении, будем улучшать методику экспериментов и, я надеюсь, в конечном счёте преуспеем.

© Habrahabr.ru