На чем основана логика? Часть 1. Алгебра множеств без аксиом19.12.2023 16:00

Сразу начну с гипотезы, положенной в основу данной статьи: вся классическая логика основана на множествах, точнее, на алгебре множеств. Должен сказать, что в современной логике и математике эта гипотеза считается ошибочной, так как еще на рубеже XIX и XX столетий сложилось убеждение (точнее, заблуждение), что понятие «множество» противоречиво. Мне представляется, что настала пора избавляться от этого и некоторых других заблуждений, связанных с логикой.

Вступление

В предлагаемой статье будут показано, как можно без противоречий использовать понятие «множество» в основаниях логики. Будет обоснована возможность доказательства законов алгебры множеств без использования аксиом, а также показано, как можно некоторые из этих законов использовать в качестве методов логического анализа. Будут обоснованы ранее неизвестные законы алгебры множеств.

Чтобы выполнить эти задачи, пришлось взять за основу не абстрактный и труднопонимаемый вариант теории множеств (Цермело — Френкеля, Неймана — Бернайса — Геделя, Тарского — Гротендика и др.), а «примитивный» вариант, который был предложен в книге, вышедшей впервые в 1941 году и до сих пор еще не утратившей своей популярности. Речь идет о книге Р. Куранта и Г. Роббинса «Что такое математика?». А «примитивный» вариант — это математическая система, которая в этой книге названа «Алгеброй множеств» (см. стр. 134 — 142 цитируемого издания). Система достаточно проста — ее легко могут усвоить школьники младших классов.

В Части 1 показано обоснование законов алгебры множеств без аксиом на основе определений операций и отношений.

В Части 2 мы убедимся, что эта «примитивная» система позволяет не только строго обосновать силлогистику и полисиллогистику, но и значительно расширить их аналитические возможности.

В Части 3 будет показано, что при подключении к алгебре множеств некоторых малоизвестных свойств декартова произведения множеств мы получим все законы и методы исчисления высказываний, а также значительную часть законов и методов исчисления предикатов. Для «примитивного» варианта, согласитесь, это немало.

А чтобы наслаждаться сложностями и парадоксами, без которых не мыслят математику многие профессионалы (актуальная бесконечность, гипотеза континуума, парадокс Банаха — Тарского о равновеликом удвоении шара и др.), достаточно продолжить эту «примитивную» теорию, добавив в нее соответствующие аксиомы теории множеств.

Поймите, я не призываю расшатывать основы современной логики, я просто предлагаю начать ее с более простого и общедоступного варианта учения о множествах. И посмотреть, что мы в результате получим.

Что понимается под алгеброй множеств

В настоящее время термин «алгебра множеств» неоднозначен. В русскоязычной математической литературе под ним чаще всего понимается система подмножеств некоторого множества с операциями «пересечение», «объединение» и «разность». При этом не принимается во внимание, что между множествами существуют отношения «включения» и «равенства», хотя речь идет о подмножествах (т.е. отношение «включение» неявно присутствует в данном варианте определения алгебры множеств).

Такое «однобокое» и невнятное определение соответствует определению «алгебры множеств» в Математической энциклопедии, выпущенной в 1977 — 1985 годах издательством «Советская энциклопедия». Это определение остается без изменения и в современной русской Википедии (см. вариант статьи «Алгебра множеств» до даты публикации этой моей статьи).

Мне кажется, что такая «однобокость» обусловлена тем, что термин «алгебра» с точки зрения разработанной академиком А.И. Мальцевым теории алгебраических систем подразумевает систему объектов, в которой определены только операции. Что касается отношений, то с точки зрения этой теории в алгебре их не должно быть. Курант и Роббинс в своей книге не учли этот «запрет». Это можно объяснить тем, что книга «Что такое математика?», в которой определена алгебра множеств, была впервые издана в 1941 году, когда теория алгебраических систем еще не была известна!

В англоязычной литературе под алгеброй множеств понимается система, в которой помимо операций определены отношения включения и равенства, что соответствует описанию алгебры множеств в книге Р. Куранта и Г. Роббинса.

Иногда алгебру множеств отождествляют с «наивной теорией множеств», ставшей широко известной после публикации в 1960 году книги Пола Халмоша». Однако эта отождествление не вполне корректно. В своей книге Халмош излагает понятным для студентов языком один из вариантов аксиоматической теории множеств. А в книге «Что такое математика?» алгебра множеств — это математическая система с определенными операциями и отношениями, законы которой, как считают авторы книги, можно обосновать без аксиом.

Алгебра множеств как альтернатива аксиоматическим системам

Современную математику невозможно представить без термина «множество» — он прочно укрепился практически во всех ее основных разделах, включая математическую логику. Есть веские основания полагать, что законы алгебры множеств можно использовать в качестве математической модели семантики.

На рубеже XIX и XX столетий были попытки положить «множество» в основу всей математики, но не получилось, так как примерно в то же время были обнаружены многочисленные парадоксы, многие из которых тесно связаны с понятием «множество». Чтобы оберечься от этого кошмара, была придумана и безоговорочно принята в качестве оснований логики и математики Теория формальных систем, а также ее детище — Язык первого порядка, который лежит в основе современной математической логики.

Результатом этих событий стало то, что слово «множество» в основаниях современной логики оказалось под запретом. Хотя на самом деле под запретом оказалось не понятие «множество», а термин «множество», поскольку в многочисленных современных учебниках по логике используются для обоснований диаграммы Венна, модельные схемы, семантические схемы, круги Эйлера и т.д., которые, по сути, являются ничем иным, как наглядными отображениями соотношений между множествами.

В математической логике помимо аксиом предусмотрены правила вывода, причем и те, и другие никак не обоснованы. Мы просто должны поверить, что так надо. А что тогда нам мешает изменить эти аксиомы и правила вывода и получить бесчисленные варианты неклассических логик? В принципе так и получилось в современной науке, в результате чего «строгая» наука пришла к тому, что теперь у нас нет четких критериев выбора правильной логики для анализа рассуждений и обоснований.

Далее мы увидим, что в этом отношении алгебра множеств отличается от аксиоматических теорий тем, что в ней законы и правила логического вывода можно обосновать без аксиом. Это свойство алгебры множеств, а также полное совпадение ее законов с законами классической логики можно считать веским доводом в пользу того, что именно классическая логика является правильной логикой.

Основные понятия и законы алгебры множеств

Для тех, кто не изучал алгебру множеств или забыл ее, подробное и понятное для многих изложение ее основных понятий (множество, элемент, отношение включения множеств, пустое множество, операции дополнения, пересечения и объединения, законы алгебры множеств) можно найти в главе «Алгебра множеств» цитируемой выше книги Куранта и Роббинса. Книга доступна в Интернете. В данной статье приведены лишь краткие определения и современные обозначения.

Отношения в алгебре множеств

Такое «отрицательное» определение обусловлено тем, что допускается случай, когда множество A не содержит элементов, т.е. является пустым множеством (A = \varnothing). Тем самым из этого определения следует, что пустое множество включено в любое множество.

  • Строгое включение. Разновидностью отношения включения множеств является строгое включение (\subset), когда A \subseteq B, но при этом точно известно, что в множестве B существует хотя бы один элемент, который не является элементом множества A.

Рассмотрим вкратце, почему в алгебре множеств можно не опасаться парадоксов. В теории множеств отношение принадлежности является основным. Одна из аксиом теории множеств позволяет использовать множества в качестве элементов. Это означает, что в теории множеств, если не вводить ограничений в виде других аксиом, допустимы такие выражения, как «множество всех множеств» и «множество, являющееся элементом самого себя» (самоприменимое множество), которые и вызывают парадоксы. В то же время в алгебре множеств отношение принадлежности вспомогательное и служит лишь для описания или определения конкретных множеств. И в ней не предписано отождествлять элемент и множество (ниже приведено одно важное исключение из этого правила).

Основным (системообразущим) в алгебре множеств является отношение включения. Его «самоприменимость» (A \subseteq A) является одним из законов алгебры множеств и не влечет парадоксов.

  • Отношение равенства множеств. Помимо включения в алгебре множеств определено отношение равенства. Если множества содержат небольшое число элементов, то их равенство можно установить с помощью сравнения содержащихся в них элементов. Если элементов много или множества заданы с помощью описания свойств, то можно установить равенство двух множеств (допустим, A = B), если доказать справедливость отношений A \subseteq B и B \subseteq A. Этот метод доказательства основан на одном из законов алгебры множеств.

Операции алгебры множеств

Во многих случаях предполагается, что анализ соотношений между множествами выполняется в рамках некоторого универсального множества, называемого универсумом. Обозначим его \bf{\it{U}}.

Например, если \bf{\it{U}}= \{a, b, c, d\}, а S = \{ a, c, d\}, то \overline{S} = \{b\}.

Например, если K = \{b, d\}, L = \{b, c, d\} и M = \{a, c\}, то K \cap L = \{b, d\},
K \cap M = \varnothing.

  • Объединение множеств. Объединением двух множеств (например, A и B) называется операция (обозначается A \cup B), в результате которой образуется множество, содержащее те и только те элементы, которые содержатся хотя бы в одном из этих множеств.

Например, если K = \{b, d\}, L = \{a, c, d\}, то K \cup L = \{a, b, c, d\}.

Элементы в множествах не повторяются. В противном случае это будет уже другой математический объект — мультимножество, законы которого существенно отличаются от законов алгебры множеств.

Законы алгебры множеств

В книге «Что такое математика?» перечислено 26 законов алгебры множеств. Все они приведены ниже. Пусть A, B и C — произвольные множества, \bf{\it{U}} — универсум рассуждения и \varnothing — пустое множество.
1) A \subseteq A.
2) Если A \subseteq B и B \subseteq A, то A = B.
3) Если A \subseteq B и B \subseteq C, то A \subseteq C.
4) \varnothing \subseteq A. \qquad \qquad \qquad \qquad \qquad \qquad 5) A \subseteq \bf{\it{U}}.
6) A \cup B = B \cup A. \qquad \qquad \qquad \qquad \: 7) A \cap B = B \cap A.
8) A \cup (B \cup C) = (A \cup B) \cup C. \qquad \quad \; 9) A \cap (B \cap C) = (A \cap B) \cap C.
10) A \cup A = A. \qquad \qquad \qquad \qquad \qquad 11)A \cap A = A.
12) A \cap (B \cup C) = (A \cap B) \cup (A \cap C). 13) A \cup (B \cap C) = (A \cup B) \cap (A \cup C).
14)A \cup \varnothing = A. \qquad \qquad \qquad \qquad \qquad 15)A \cap \bf{\it{U}}= A.
16) A \cup \bf{\it{U}} = \bf{\it{U}}. \qquad \qquad \qquad \; \qquad \quad \; 17) A \cap \varnothing = \varnothing.
18) A \subseteq B эквивалентно A \cup B = B и эквивалентно A \cap B = A.
19) A \cup \overline{A} = \bf{\it{U}}. \qquad \qquad \qquad \qquad \qquad 20) A \cap \overline{A} = \varnothing.
21) \overline{\varnothing} = \bf{\it{U}}. \qquad \quad \qquad \qquad \qquad \qquad \quad 22) \overline{\bf{\it{U}}} = \varnothing.
23) \overline{\overline{A}} = A.
24) A \subseteq B эквивалентно \overline{B} \subseteq \overline{A}.
25) \overline{A \cup B}= \overline{A} \cap \overline{B}. \qquad \qquad \qquad \qquad 26) \overline{A \cap B}= \overline{A} \cup \overline{B}.

В литературе закон 3 называют законом транзитивности включения множеств, законы 12 и 13 — законами дистрибутивности, закон 23 — законом инволюции дополнения, закон 24 — законом контрапозиции, а законы 25 и 26 — законами де Моргана. В логике закону 19 соответствует закон исключенного третьего, а закону 20 — закон непротиворечия.

Обоснование законов алгебры множеств без аксиом

В книге Куранта и Роббинса говорится о том, что проверить справедливость этих законов можно с помощью «самой элементарной логики». Под этим понимается перебор вариантов соотношений между множествами. Эти соотношения можно отобразить с помощью диаграмм Венна. Рассмотрим этот способ на примере вывода некоторых законов алгебры множеств. На рисунке ниже показана диаграмма Венна, с помощью которой можно выразить все возможные соотношения между двумя множествами A и B с учетом их общего универсума \bf{\it{U}}.

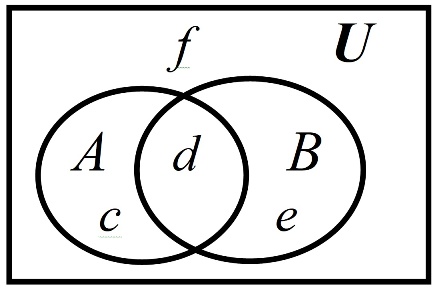
Диаграмма Венна для двух множеств

Диаграмма Венна для двух множеств

Выделим на рисунке области c, d, e и f, не имеющие внутренних границ. Ясно, что эти области не пересекаются друг с другом, а их объединение равно \bf{\it{U}}. Тем самым они образуют разбиение универсума. Это означает, что полученные в результате разбиения множества никак не связаны между собой. К тому же с их помощью можно единственным способом представить множества \bf{\it{U}}, A и B, поэтому их можно использовать в качестве элементов этих множеств. Тогда для доказательства законов алгебры множеств можно взять за основу следующие исходные данные: \bf{\it{U}}= \{c, d, e, f\}; A = \{c, d\}; B = \{d, e\}.

Здесь можно избежать сомнительного использования множеств в качестве элементов. Для этого достаточно представить, что c, d, e и f — это просто обозначения соответствующих множеств (кавычки в обозначениях подразумеваются). Тогда все последующие операции с ними в качестве элементов будут уже не с множествами, а с обозначениями.

Для этих исходных данных докажем один из законов де Моргана: \overline{A \cup B}= \overline{A} \cap \overline{B}. Для этого в соответствии с определениями операций последовательно выполним следующие вычисления.

  1. A \cup B = \{c, d, e\};

  2. \overline{A \cup B} = \{f\};

  3. \overline{A} = \{e, f\};

  4. \overline{B} = \{c, f\};

  5. \overline{A} \cap \overline{B} = \{f\};

  6. Сравним 2 и 5. В результате получим: \overline{A \cup B}= \overline{A} \cap \overline{B}.

Вычисления подтверждают справедливость закона де Моргана. Однако этого недостаточно, так как необходимо проверить этот закон для всех возможных вариантов соотношений между множествами A и B. Эти варианты можно получить, если последовательно исключать элементы c, d, e и f и их сочетания из универсума \bf{\it{U}}. Нетрудно убедиться, что таких вариантов 16. Для ясности перечислим их.

  1. \bf{\it{U}}= \{c, d, e, f\}; A = \{c, d\}; B = \{d, e\}.

  2. \bf{\it{U}}= \{c, d, e\}; A = \{c, d\}; B = \{d, e\}.

  3. \bf{\it{U}}= \{c, d, f\}; A = \{c, d\}; B = \{d\}.

  4. \bf{\it{U}}= \{c, e, f\}; A = \{c\}; B = \{e\}.

  5. \bf{\it{U}}= \{d, e, f\}; A = \{d\}; B = \{d, e\}.

  6. \bf{\it{U}}= \{c, d\}; A = \{c, d\}; B = \{d\}.

  7. \bf{\it{U}}= \{c, e\}; A = \{c\}; B = \{e\}.

  8. \bf{\it{U}}= \{c, f\}; A = \{c\}; B = \varnothing.

  9. \bf{\it{U}}= \{d, e\}; A = \{d\}; B = \{d, e\}.

  10. \bf{\it{U}}= \{d, f\}; A = \{d\}; B = \{d\}.

  11. \bf{\it{U}}= \{e, f\}; A = \varnothing; B = \{e\}.

  12. \bf{\it{U}}= \{c\}; A = \{c\}; B = \varnothing.

  13. \bf{\it{U}}= \{d\}; A = \{d\}; B = \{d\}.

  14. \bf{\it{U}}= \{e\}; A = \varnothing; B = \{e\}.

  15. \bf{\it{U}}= \{f\}; A = \varnothing; B = \varnothing.

  16. \bf{\it{U}}= \varnothing; A = \varnothing; B = \varnothing.

Например, докажем справедливость закона де Моргана для варианта 8:
\bf{\it{U}}= \{c, f\}; A = \{c\}; B = \varnothing.

  1. A \cup B = \{c\};

  2. \overline{A \cup B}=\{f\};

  3. \overline{A} = \{f\};

  4. \overline{B} = \{c, f\};

  5. \overline{A} \cap \overline{B} = \{f\};

  6. Сравним 2 и 5. В результате получим: \overline{A \cup B}= \overline{A} \cap \overline{B}.

Рассмотрим некоторые варианты доказательства закона контрапозиции (номер 24). В этом законе соотношение A \subseteq B является обязательным условием, поэтому необходимо рассматривать только те варианты соотношений между множествами A и B, в которых соблюдается это соотношение. К ним относятся следующие 8 вариантов
5) \bf{\it{U}}= \{d, e, f\}; A = \{d\}; B = \{d, e\}.
9) \bf{\it{U}}= \{d, e\}; A = \{d\}; B = \{d, e\}.
10) \bf{\it{U}}= \{d, f\}; A = \{d\}; B = \{d\}.
11) \bf{\it{U}}= \{e, f\}; A = \varnothing; B = \{e\}.
13) \bf{\it{U}}= \{d\}; A = \{d\}; B = \{d\}.
14) \bf{\it{U}}= \{e\}; A = \varnothing; B = \{e\}.
15) \bf{\it{U}}= \{f\}; A = \varnothing; B = \varnothing.
16) \bf{\it{U}}= \varnothing; A = \varnothing; B = \varnothing.

Докажем этот закон для варианта 5.

  1. Убедимся, что A \subseteq B: \{d\} \subseteq \{d, e\};

  2. \overline{A} = \{e, f\};

  3. \overline{B} = \{f\};

  4. проверка показывает, что \overline{B} \subseteq \overline{A}.

Нетрудно убедиться, что закон контрапозиции подтверждается и для всех других перечисленных вариантов.

Разумеется, предложенный метод доказательства, в котором используется «тупой» перебор вариантов, многим может показаться весьма трудоемким. Например, чтобы доказать законы дистрибутивности, в которых участвуют 3 множества, потребуется рассмотреть 256 вариантов в каждом случае. Можно сократить число вариантов, если для доказательства этого закона воспользоваться другими, менее трудоемкими при обосновании, законами алгебры множеств. Идею такого доказательства законов дистрибутивности можно найти в книге Роберта Р. Столла «Множества. Логика. Аксиоматические теории» (стр. 29).

Однако, несмотря на большой объем вычислений, несомненное преимущество этого метода в том, что он ясно показывает возможность строгого доказательства законов алгебры множеств без аксиом. Тем самым мы получаем систему, в которой можно не сомневаться.

Дизайн баннера выполнен Анной Горской

© Habrahabr.ru