Монады как паттерн переиспользования кода02.03.2020 10:53

В предыдущей статье мы обсуждали, почему функциональное программирование это совсем не то, что распиарено, и что оно совершенно не противоречит ООП, так, что даже сам Фаулер пишет про хороший ФП дизайн порождающий хороший ООП дизайн программы (и наоборот).

Сейчас же я хочу рассказать, что такое монады на самом деле, чем они полезны для обычного практикующего разработчика, и приведу примеры, почему недостаточная поддержка их в распространенных языках приводит к копипасте и ненадежным решениям.

Но ведь в интернете буквально сотни статей про ФП и монады, зачем писать еще одну?

Дело в том, что все их (по крайней мере те что я читал) можно поделить условно на две категории: с одной стороны это статьи где вам объяснят что монада это моноид в категории эндофункторов, и что если монада T над неким топосом имеет правый сопряжённый, то категория T-алгебр над этой монадой — топос. На другой стороне располагаются статьи, где вам рассказывают, что монады — это коробки, в которых живут собачки. кошечки, и вот они из одних коробок перепрыгивают в другие, размножаются, исчезают… В итоге за горой аналогий понять что-то содержательное решительно невозможно.

Получается, что первые обычно полезны тем, кто и так знает обсуждаемую тему, а вторые даже не знаю на кого рассчитаны: сколько я их не прочитал, ничего полезного понять из них мне не удалось.

Я же хотел бы занять промежуточную позицию, и рассказать про монады без заумных терминов, но и без котиков, используя понятные ООП разработчикам термины: интерфейсы, паттерны, копипаста, инкапсуляция сложности, бойлерплейт, и так далее. В процессе работы над статьёй ни один термин теории категории использован не был.

Вступление

Итак, с чего бы начать? В нашем случае имеет место проблема курицы и яйца: чтобы мотивировать узнать про монады, я должен привести примеры их использования, но чтобы привести примеры использования, вы должны их уже знать. Поэтому я попрошу вас набраться немного терпения, и сначала узнать, что же это такое, а потом уже я обещаю показать, почему это знание полезное, и как его можно применить на практике.

Я долго думал на каком языке писать примеры, перебрал все варианты, которые знал. В итоге остановился на модифицированном C#. Scala оказалась слишком вербозной, Rust хотя и имеет концепцию трейтов, не может выразить самый простой из требуемых тайпклассов, ну, а Haskell знают не все.

Но обычный сишарп не обладает нужными фичами, поэтому в статье я буду использовать синтаксис C# 10 (который еще не вышел), в частности расширение Shapes и расширение HKT. Первый из них добавляет в язык шейпы (aka тайпклассы, aka трейты). Если привести пример зачем они нужны, то вот так мы могли бы объявить тайпкласс для того, чтобы помечать классы как сериализуемые

public shape JsonDeserialize
{
    static T Deserialize(JObject input);
}

Такой тайпкласс превратил бы рантайм эксепшн JsonSerializationException: Could not create an instance в ошибку времени компиляции. Лично я с этой ошибкой часто встречаюсь на проектах с десириализацией нетривиальных типов в кастомных форматах, поэтому и пример про него.

Шейпы отличаются от интерфейсов двумя особенностями: во-первых, они позволяют объявлять статические методы (и даже константы), а не только инстансные, а во-вторых, позволяют расширять чужие классы. Например, ICollection не наследует IReadOnlyCollection, и мы ничего с этим не можем поделать. Будь они тайпклассами, мы легко могли бы зачинить эту проблему. Или мы можем расширить функциональность стандартных классов. Если вы когда-нибудь хотели написать генерик-функцию вида where T : Number, работающую с любыми числами, то вы сразу должны оценить, какая это нужная штука: с тайпклассами объявить такой Number не составляет никаких проблем.

Второе расширение нам поможет работать с открытыми генерик-аргументами как типами. Например, это может выглядеть так:

public static T CreateSomethingOfInts() where T : <>, new() 
{
    return new T();
}

Возможно, выглядит страшновато, но просто посмотрите на пример использования, и всё станет понятно:

// можем создать инстанс любого типа с одним генерик параметром

var list = CreateSomethingOfInts();
var hashSet = CreateSomethingOfInts();
// …
// Array, Nullable, LinkedList, ... - можно использовать любой подобный тип
// получим в результате Array, Nullable, LinkedList, ...

Ко всему этому в статье будут ссылки на плейграунд с реализацией на актуальном C# 8. Они явно выигрывают в том, что их можно запускать, однако пользы в таком виде от них не очень много. Они приложены только для лучшего понимания написанного, потому что их можно позапускать и потыкать в дебаггере.

Что ж, прелюдия довольно ощутимо затянулась, приступим.

Functor

И первое с чего мы начнем — с функтора. «Как же так, ты же про монады рассказать обещал!» — скажете вы. Да, но функтор базовый строительного блока многих ФП понятий, в том числе и монады, поэтому без него не обойтись.

Итак, что такое функтор? Можно долго рассуждать в терминах объектов категорий и морфизмов между ними, а можно взять наш понятийный аппарат ООП разработчиков и сказать, что Функтор — это любой объект, реализизующий тайпкласс Functor следующего вида:

public shape Functor where T : <>
{
    static T Map(T source, Func mapFunc);
}

Собственно, это всё. Это полное определение, прочитав которое вы можете смело сказать «я знаю, что такое функтор». Если бы терминологию придумали джависты, то они назвали бы его Mappable, потому что он, собственно, определяет единственный метод Map, который позволяет преобразовать наш тип-контейнер, параметризованный типом A, в такой же контейнер, но уже с элементами типа B.

Например, был у нас массив чисел и функция ToString, получили массив строк. Или был список строк, а получили список длин этих строк. А может и не список, и не массив, а стек какой-нибудь. Суть одна — у нас есть наша структура данных, в которой лежат какие-то объекты. У нас есть функция A => B, которая преобразует один такой объект в другой такой объект. Тогда с использованием функции Map мы можем сделать такой же контейнер, как тот, что хранит A, но теперь в нём будут B.

Для Map сущестует единственное правило: если наша mapFunc это Identity-функция вида x => x, то контейнер должен остаться неизменным. То есть, чтобы считаться «законным» функтором, для нашего контейнера всегда должно выполняться вот это равенство:

Map(something, x => x) === something

Это правило достаточно очевидное, оно, по сути, говорит, что сам контейнер по себе ничего со значением не делает, и всё взаимодействие с его элементами мы можем контролировать при помощи mapFunc. Там нет никаких рандомов, внешних взаимодействий, и так далее, мы можем безопасно вызывать Map как угодно.

Давайте подумаем какие типы из стандартной библиотеки удовлетворяют этому правилу?
Ну, самое простое, это итераторы:

public extension EnumerableFunctor of IEnumerable : Functor { public static IEnumerable Map(IEnumerablesource, Func map) => source.Select(map); } // проверяем закон функторов var range = Enumerable.Range(1, 10); Console.WriteLine(Map(range, x => x).SequenceEquals(x)) // выведет True

Раз этот код компилируется и тест проходит, то мы доказали, что итератор в дотнете является функтором! Хотя в дотнете нет тайпклассов, тем не менее IEnumerable — это функтор, раз закон выполняется

Какой еще тип может вести себя подобным образом? Подумайте немного, вы с ним работаете каждый день по 100 раз на дню.

Скрытый текст
И конечно же это Nullable. Давайте реализуем для него тайпкласс функтора:
public extension NullableFunctor of Nullable : Functor { public static B? Map(A? source, Func map) => source is A notNullSource ? map(notNullSource) : default(B?); } // проверяем закон функторов int? nullableTen = 10; int? nullableNull = null; Console.WriteLine(Map(nullableTen, x => x) == nullableTen); // выведет True Console.WriteLine(Map(nullableNull, x => x) == nullableNull); // выведет True
Ссылка на плейграунд
Таким образом мы доказали, что Nullable — это тоже функтор.
Другой очевидный ответ — Task, для него нетрудно реализовать Map самостоятельно.

В учебниках по ФП часто упоминают про еще один закон для функторов, но тут есть один нюанс: если вы соблюдаете первый закон, то второй соблюдается автоматически. Это математический факт, так называемая «бесплатная теорема». Так что для того, чтобы проверить является ли наш класс функтором, достаточно проверить только одно простое правило, которое мы обсудили.

Map позволяет абстрагироваться от структуры контейнера, давая способ менять содержимое контейнера, ничего про эту структуру не зная

Вот мы и познакомились с одним из страшнейших зверей мира ФП — целым функтором! А дальше нас ждет ещё более сложный тайпкласс и зовут его…

Applicative

Аппликативный функтор! Который определяет не один метод, а целых два:

public shape Applicative where T : <> { static TPure(A a); static T LiftA2(T ta, T tb, Func map2); }

Что мы тут видим? Аппликативный функтор, это любой тип, который умеет:

Создаваться из одного значения любого типа. По сути аналогичен констрейнту where T : new(), за исключением того, что new() не принимает аргументов, а мы принимаем один.

А тут уже интересно. Интерфейс говорит нам, что если у нас есть два значения T и T и функция, преобразующая пару значений A, B в C, то мы можем получить T. Название LiftA2 происходит из того, что мы как бы «поднимаем» вычисление над двумя голыми переменными A и B в вычисление над аппликативами T и T соответственно.

Непонятно? Давайте разбираться. Самый простой способ разобраться в чем-то — сделать это что-то своими руками. Класс называется аппликативный функтор, в предыдущем разделе мы как раз пару функторов разобрали, возможно, они как-то связаны?

«Talk is cheap, show me the code», поэтому в качестве доказательства что наш класс является аппликативом мы, как и раньше, постараемся просто реализовать соответствующий интерфейс. Если компилятор нас не остановит — то значит мы успешно доказали то, что хотели, если же у нас в какой-то момент возникнут трудности — значит мы не правы. Давайте начнем с итератора:
public extension EnumerableApplicative of IEnumerable : Applicative { static IEnumerablePure(A a) => new[] { a }; static IEnumerable LiftA2(IEnumerable ta, IEnumerable tb, Func map2) => ta.SelectMany(a => tb.Select(b => map2(a, b))); }

Ну, вроде у нас всё получилось. Что интересно — всё это дело прекрасно компилируется восьмым сишарпом, если закомментировать часть про public extension. То есть в обычном кроваво-энтерпрайзном языке есть давно все эти прелести, просто они не оформлены в виде тайпкласса, от которого можно абстрагироваться (зачем это вообще может понадобиться я покажу ниже).

Что же насчёт Nullable? Тоже никаких проблем:
public extension NullableApplicative of IEnumerable : Applicative { static A? Pure(A a) => a; static C? LiftA2(A? ta, B? tb, Func map2) => (ta, tb) switch { (A a, B b) => map2(a, b), // Если оба не null - то вычисляем _ => default(C?) // кто-то нулл - результат null }; }

В примере с итератором выше мы релизовали семантику «каждый с каждым», но мы все прекрасно знаем, что есть другая равнозначная семантика «первый с первым, второй со вторым, …». К сожалению, реализовать один и тот же интерфейс для одного типа двумя различными способами нельзя, поэтому нам подойдет паттерн Адаптер, который в ФП мире называют ньютайп. Для итератора таким адаптером является класс ZipList:

public class ZipList : IEnumerable { private IEnumerable _inner; // .. конструктор и реализация IEnumerable опущена для краткости } public extension ZipListApplicative of ZipList : Applicative { static IEnumerablePure(A a) => // вообще тут должен быть бесконечный генератор элемента 'a' Enumerable.Repeat(a, int.MaxValue); static IEnumerable LiftA2(IEnumerable ta, IEnumerable tb, Func map2) => ta.Zip(tb, map2); }

Оказывается, ZipList давно существует в стандартной поставке, просто очень хорошо скрывается. Но без общего зонтичного типа Applicative он не особо полезен, поэтому дотнет обходится просто одинокой функцией Zip.
Мы узнали, что такое аппликативы, а какие-нибудь примеры использования будут? Что мы можем с ними сделать? Ну, с ними можно много чего интересного делать — библиотеку парсер-комбинаторов с их помощью удобно выражать, проперти-тест фреймворк можно написать, но для статьи такие примеры слишком большие, поэтому давайте возьмем чего-нибудь попроще. Например, можно написать функцию, которая из пары аппликативных функторов нам сделает аппликатив пары оригинальных значений, то есть: (F, F) -> F<(A, B>). Давайте напишем:
public static T<(A, B)> Combine(Tta, T tb) => LiftA2(ta, tb, (a, b) => (a, b)); var eta = Enumerable.Range(3, 2); var etb = Enumerable.Range(15, 4); int? nta = 10; int? ntb = null; Combine(eta, etb) // [(3, 15), (3, 16), (3, 17), (3, 18), (4, 15), (4, 16), (4, 17), (4, 18)] Combine(nta, nta) // (10, 10) Combine(nta, ntb) // Null Combine(new ZipList(eta), new ZipList(etb)) // [(3, 15), (4, 16)]

Ссылка на плейграунд

С одной стороны, функция простая, можно даже сказать скучная. А с другой — посмотрите, мы написали очень абстрактную функцию Combine, которая совершенно ничего не знает о переданных значениях, но при этом умеет производить очень сильно различающиеся действия. Для двух списков она считает комбинаторику всех пар, для нуллейблов оно возвращает либо пару элементов, если оба переданных параметра имели значение, либо null. Для ZipList мы сцепили соответствующие элементы двух списков, причем результирующий список был усечен до самого короткого из двух. Таким образом, аппликатив позволяет нам разделить действие над элементами контейнера (это наша функция (a, b) => (a, b)) и форму контейнера (это T<>). То есть, с одной стороны, мы можем описывать вычисления, не заботясь о форме контейнера (опциональное значение/список/промис/что угодно), а с другой мы, наоборот, можем реализовать некий контейнер, а варианты работы с этим контейнером оставить на откуп клиентскому коду.

Остаётся добавить, что еще есть всякие законы, которые должны выполняться, но они достаточно очевидны, вроде ассоциативности операций и так далее. Чтобы не раздувать текст статья я их доказывать не буду, потому что, по сути, эти законы просто проверяют соблюдение «Принципа наименьшего удивления». Можно почитать про них по ссылке и удостовериться, что они накладывают достаточно ожидаемые ограничения.

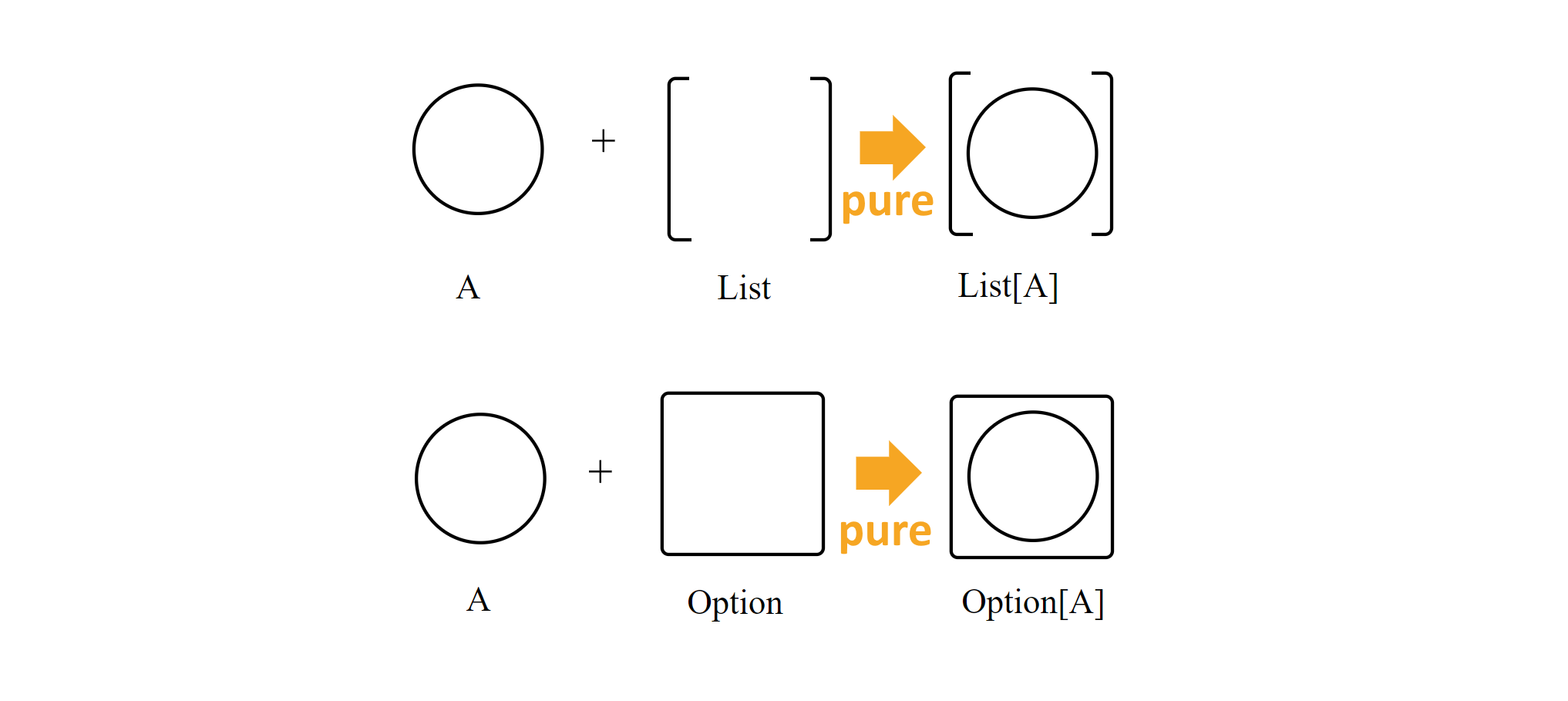
pure позволяет нам создать контейнер, содержащее единственное значение

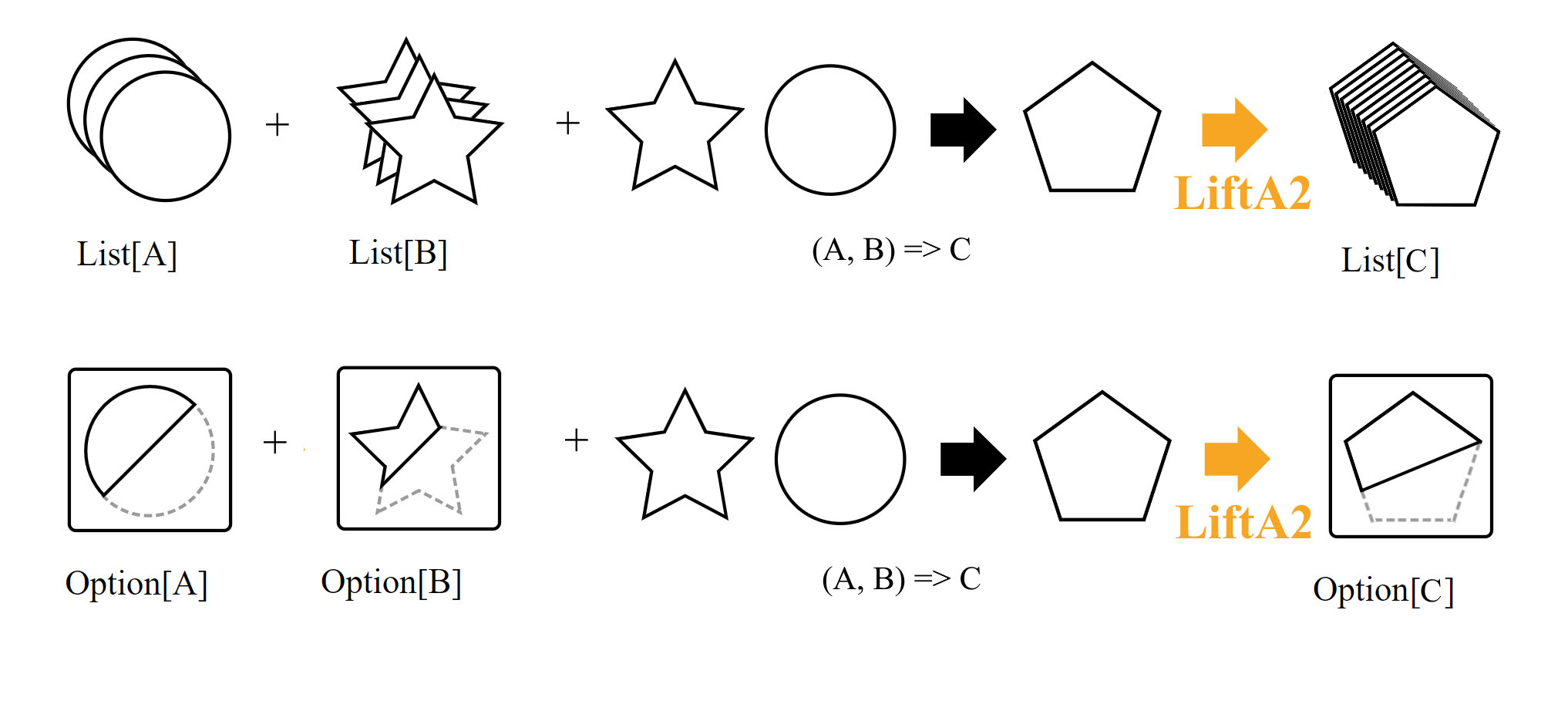
liftA2 позволяет нам использовать функцию от двух аргументов, имея на руках
два контейнера с соответствующими типами, упакованными внутри

Прежде, чем мы приступим к герою сегодняшнего дня, хочу обратить внимание, что тайпкласс который мы только что обсудили называется «Аппликативный функтор». Почему именно так? «Аппликативный» означает что с ним мы можем применять упакованные функции к упакованным значениям. Например, у нас может быть список функций, и список значений. Применив к ним LiftA2 мы получим список результатов каждой функции примененной к каждому значению. Ну, это нужно бывает не часто, а вот из двух опциональных значений сделать третье, если в обоих не null — буквально каждый день. Или выполнить две асинхронные операции и вычислить на их основании какой-то ответ.

А почему функтор? Имея функции LiftA2 и Pure легко реализовать Map:
static T MapAnyFunctor(Tsource, Func map) where T : Applicative => LiftA2(source, Pure(0), (a, _) => map(a));

Как это работает? Очень просто — мы создаем мусорное значение и с помощью функции Pure оборачиваем его в аппликатив T<>. Теперь у нас есть T и T<НашМусорныйТип>, которые по типам подходят для LiftA2. Нам остаётся только её вызвать, а в передаваемом коллбеке игнорировать это мусорное значение, вызывая map для элементов настоящего контейнера T. Написав эту функцию мы доказали, что любой функтор является аппликативом. Можно дополнить нашу изначальную сигнатуру:

public shape Applicative : Functor where T : <> { static TPure(A a); static T LiftA2(T ta, T tb, Func map2); }

Ссылка на плейграунд. Можно убедиться, что поведение такое же, какое было изначально.

Бонус
Также легко реализовать тайплкасс аппликатива для Task:
public extension EnumerableApplicative of IEnumerable : Applicative { public static TaskPure(A a) => Task.FromResult(a); public static async Task LiftA2(Task ta, Task tb, Func map2) { await Task.WhenAll(ta, tb); return map2(ta.Result, tb.Result); } }
Ссылка на плейграунд

Monad

И вот он. Тайпкласс, одним своим названием повергающий в ужас. И который состоит
из целых двух функций, одну из которых мы уже знаем:
public shape Monad where T : <> { static TPure(A a); static T Bind(T ta, Func> mapInner); }

Если говорить по-русски, то:

Монада — это любой класс с функциями Pure и Bind, которая принимает аргумент типа T и функцию, преобразующую распакованное значение A в T, и возвращает значение того же типа T
И никаких моноидов в категориях эндофункторов, заметьте. Сигнатура может выглядит немного перегруженной, но она иллюстрирует простую идею: у вас есть упакованное в контейнер значение типа А. И у вас есть функция из голого A в такой же контейнер, но уже со значением B. Функция Bind позволяет «связать» эти два выражения вместе, получив из пары (T, A => T) значение T.

Таким образом монада — это простейший интерфейс, который тривиально реализовать для того же итератора, что мы в очередной раз и сделаем:
public extension EnumerableMonad of IEnumerable : Monad { static IEnumerable Bind(IEnumerableta, Func> mapInner) => ta.SelectMany(mapInner); // Pure такой же как и в аппликативе }

Легко увидеть, что Nullable тоже является монадой. А что насчет ZipList? А вот он, оказывается, не подходит: если вы попробуете для него реализовать такой интерфейс, то у вас ничего не выйдет, потому что у монад тоже есть тройка законов, которые типы должны соблюдать (хотя они тоже тривиальные).
Некоторое время назад я сделал небольшую песочницу на расте, в котором можно проверить, выполняются ли законы для произвольного типа. Можно попробовать подставить туда ZipList со своей реализацией и убедиться, что один или несколько тестов пройти не получится.

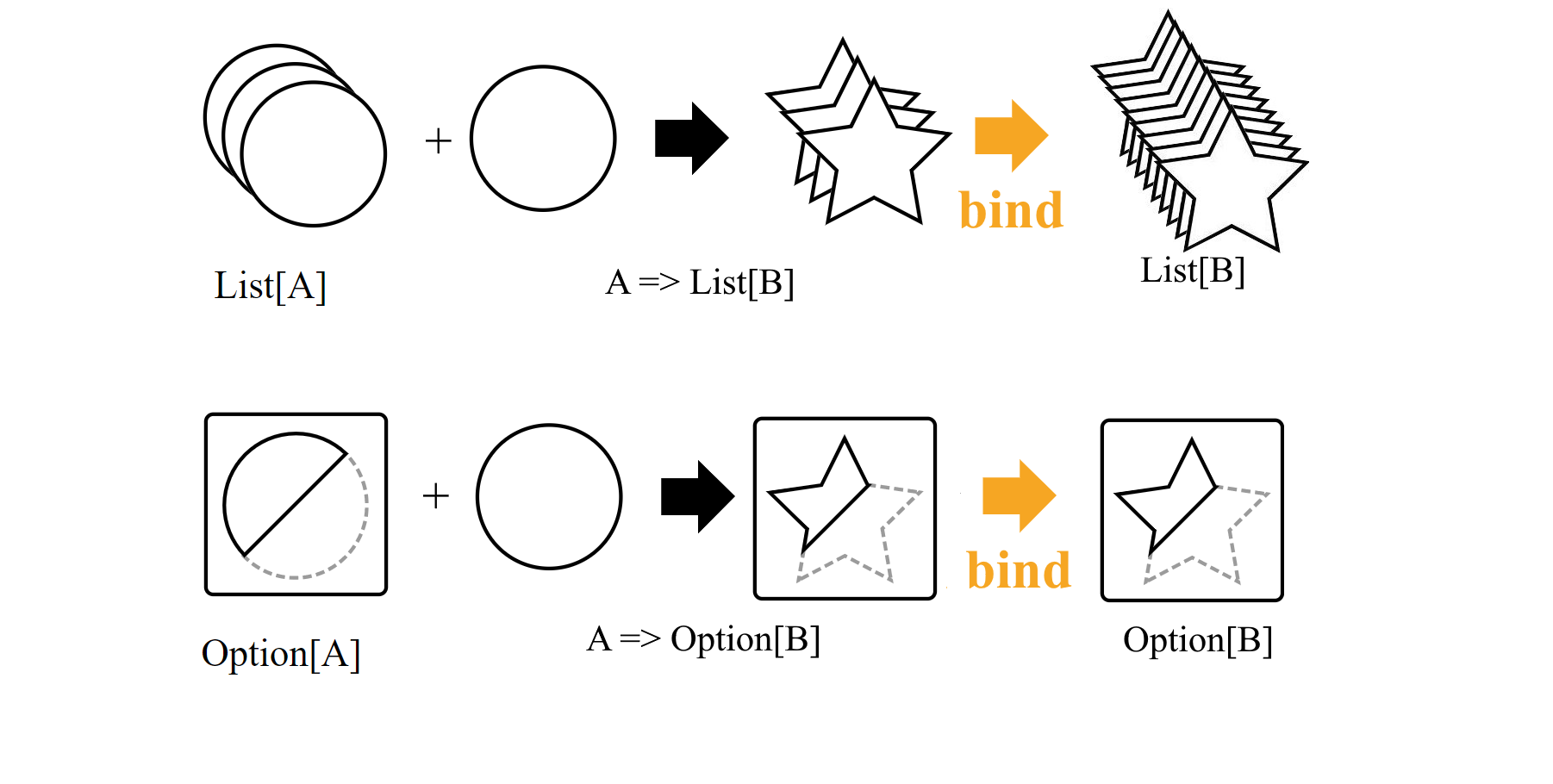
Монады позволяют имея на руках контейнер с элементами типа А и функцией из А в такой же контейнер типа В получить контейнер типа В

Любая монада также является аппликативом, поэтому реализацию Pure копипастить не надо: её можно отнаследовать от базового аппликатива. Что до LiftA2, то в качестве упражнения предлагаю реализовать её при помощи функций Pure и Bind, там нет ничего сложного.

Кроме того, что монады чрезвычайно просты, они еще и настолько полезны, что захардкожены в большинстве языков. Думаю, многим хабровчанам известно, что в хаскелле и скале есть так называемая do-нотация. Она рассахаривает такой хаскель код:

let foo = do a <- someA b <- someB pure (doSomethingWith a b)

в последовательность вызовов функции Bind которую мы только что разобрали:

var foo = Bind(someA, a => Bind(SomeB, b => Pure(DoSomethingWIth(a,b)))

Паттерн очень простой. Всё что справа от стрелочки <- идет как первый аргумент функции Bind,
то, что слева — становится именем параметра лямбды, которая передаётся как второй аргумент.
Элементарно.

Как видите, это одна простая конструкция, которая работает по одному паттерну.

А что у нас в сишарпе? А в нём есть аж целых три его захардкоженных вариации. Например, что это за код?

var values = from x in new []{ 1, 2, 3 } from y in new []{ 4, 5, 6 } select x + y;

Это ни что иное, как do-нотация для монады итератора (в хаскелле итератор называется списком):

let values = do x <- [1,2,3] y <- [4,5,6] pure (x + y)

Давайте теперь посмотрим на такой код:

var maybeA = GetMaybeA(); var maybeB = maybeA?.GetB(); var maybeC = maybeb?.GetC(); var result = maybeC;

А это do-нотация для монады Maybe (она же Option, она же с некоторой натяжкой — Nullable):

let result = do maybeA <- getMaybeA maybeB <- getB maybeA maybeC <- getC maybeB pure maybeC

Что насчет вот такого кода?

var valueA = await GetSomeA(); var valueB = await GetSomeB(valueA); var result = valueB;

А это do-нотация для монады IO (про которую мы не говорили, но, по сути, это просто аналог Task из сишарпа):

let result = do valueA <- getSomeA valueB <- getSomeB valueA pure valueB

Таким образом у нас в языке образовалось сразу три различных синтаксиса для того,
чтобы делать абсолютно одно и то же: имея на руках объект типа T<А> и функцию
из A в T, получить T, будь то A[] и A -> B[], или A? и A -> B?,
или Task и A -> Task, … И это далеко не полный перечень.

На этой ноте предлагаю перейти к первому пункту обещанного параграфа под названием…

Зачем нам монады

Упрощение синтаксиса языка

Первым пунктом, следующим из предыдущего абзаца, стоит выделить упрощение языка. Посмотрите, сколько мусора натащил сишарп, чтобы выразить простую идею «Сделай что-нибудь, а затем сделай кто-нибудь еще». И асинк-авейт, и LINQ, и null propagation являются частными случаями общей идеи. Причем которые очень часто ломаются на ровном месте. Захотел вызвать статический метод на nullable-параметре? Всё, элвис-оператор использовать не получится, пиши, как в старые-добрые времена проверку на нулл. Захотел заавейтиться внутри лямбды? Тебе компилятор скажет всё, что он думает об этой затее. Ну, хоть в случае списка, ломаться особо нечему, за исключением уродливых скобочек если нужно сделать хоть что-то выходящее за рамки LINQ-синтаксиса (например, вызвать First в конце запроса).

А еще большая проблема различного синтаксиса в том, что это всего лишь сахар: ту же функцию MapAnyFunctor написать в текущем сишарпе не выйдет. Мы годами ждали фичу async enumerable, которую наконец-таки релизнули (как всегда с кучкой костылей, все ведь например уже в курсе магических атрибутов для CancallationToken?), но сколько лет мы её ждали? Сколько человеко-лет понадобилось, чтобы её реализовать?

В языках с описываемыми возможностями системы типов это делается за день силами одного разработчика, достаточно написать адаптер для двух монад: List и IO.

Если вы думаете, что сишарп в этом плане выделяется, то спешу вас обрадовать: это не так. Тот же Rust с удовольствием прошелся по тем же граблям, и продолжает идти. Сюда относятся: и try-блоки, и Try-трейт, и всё тот же элвис-оператор, а асинк-авейт. Уверен, в будущем кортима раста будет еще годами запиливать async enumerable, как это сделала команда сишарпа, тратя кучу ресурсов на проблему, которой изначально не должно было быть.

А в другом углу ринга у нас do-нотация, которая выглядит абсолютно одинаково во всех случаях, которая позволяет всё, что позволяет родная монада, и которая состоит всего из одного ключевого слова, вместо россыпи операторов и кейвордов в случаях других языков.

И главное: при этом она базируется на интерфейсах, а не на захардкоженных в компиляторе эвристиках преобразования кода в стейт-машины. На интерфейсах, которые позволяет разработчику не ждать годами, пока команда языка соблаговолит наконец реализовать комбинатор пары монад, и которые не требуют костылить в язык кучу хаков. Что насчёт асинк энумерейбла, который автоматически параллелит получение данных по сети (мы не обсуждали, но в хаскелле для параллелизации есть монада Par)? Ну, пока ничего, ждем C# 15, в котором, возможно, это появится. А может и не появится.

Упрощение стандартной библиотеки языка

В сишарпе есть некоторое количество функций, работающих по принципу «сделай что-то, а потом еще что-то». Как мы уже выяснили, все функции такого вида отлично ложатся на монадический Bind. Это и ContinueWith, и SelectMany, и некоторые другие. Но если сишарпе их хотя бы не так уж и много, то в Rust это выглядит совершенно вопиюще. В Option/Result/Future напокопипащены буквально десятки функций, делающих ровно одно и то же, и которые могли бы быть выражены в терминах общего тайпкласса: большая часть операций через Monad, некоторые потребовали бы более редких вроде MonadFail/Bifunctor/…, но общий смысл остается тем же.

А по факту что мы имеем? Абсолютно ужасную копи-пасту в стандартной библиотеке. Вот в версии 1.29 появляется flatten для итератора, а вот спустя более чем год он же, но для опшна. Для футур он живет в стороннем крейте, который надо подключать.

Вот год назад появился transpose для Option/Result друг в друга, при том, что transpose из итератора для них появился аж в версии 0.8 в 2013 году. transpose для футур (которые как мы помним реализация IO монады для раста) до сих пор нет, еще 7 лет подождем, и они появятся.

Продолжать можно ещё долго, но суть остается прежней: можно было реализовать Monad трейт один раз, и дальше эти transpose/flatten/... появлялись бы во всех совместимых типах автоматически. Да, для конкретных классов реализация по-умолчанию может быть не оптимальной, но ведь всегда можно выполнить специализацию, особенно в стандартной библиотеке. В итоге имеется огромная проблема, которой в языке от 2015 года вообще не должно было быть изначально. Но, монад нет, и починить это в текущей версии языка невозможно, остается только копипастить однотипные реализации из типа в тип.

Сишарп тут в абсолютно схожей ситуации. Посмотрите на вот этот пакет System.Linq.Async. Разработчики из майкрософта в нём занимаются буквально тем, что копипастят реализацию LINQ из corefx, расставляя где надо async-await. Ну, там всё немного сложнее, но суть та же. Это еще один пример библиотеки, которой никогда не должно было существовать. Люди пишут руками код, который компиляторы давным-давно научились генерировать. Уже в первых версиях хаскелля были комбинаторы filterM/mapM/whateverM, которые как вы можете догадаться по их названию позволяют сделать фильтрацию/маппинг/… коллекции, производя при этом монадический эффект (отсюда буковка M в конце), в случае обсуждаемой библиотеки этим эффектом был бы асинхронный запрос.

Однако, не стандартной библиотекой единой живы, и наш следующий пункт

Сторонние библиотеки

Благодаря тому, что тайпкласс Monad (да и в целом тайпклассы) чрезвычайно абстрактный, можно создавать совершенно потрясающие удобные библиотеки. Например, возможно, вы помните мою статью, где я попробовал написать простенькое приложение на хаскелле и на го. В комментариях мне справделиво указали на то, что сравнение было «нечестным» — в го я старательно писал всё с нуля, в процессе чего я собственно несколько раз и ошибся, а в хаскелле я взял пару библиотек (для работы с деревьями и последовательностями), и написал только пару строчек, которая их склеивает вместе, где ошибиться было просто негде, ну оно и заработало как надо.

Но в тех же комментариях один из хабровчан дал замечательный ответ, который объясняет, что вовсе не случайно в хаскеле такие библиотеки есть, а в Go нет. Именно возможность спрятать конкретные реализации за тайпклассами Functor/Applicative/Monad/… и позволяет таким библиотекам существовать. Нет тайпклассов и HKT — не будет крутых библиотек, зато нужны будут разработчики, которые на зарплате будут копипастить реализации для новых конкретных монад, буде условному майкрософту или мозилле вздумается добавить их в язык. И, в отличие от общего решения, они будут это делать для тех кейсов, которые сочтут достойными. Если ваша монада не такая популярная, как список или опциональное значение, то останетесь без удобного способа смоделировать предметную область.

Для опытных шарпистов, кстати, это вовсе не новость. Например, есть куча полезных библиотек, на базе IEnumerable. Не будь такого интерфейса — не было бы и их. Куча удобных ORM в сишарпе основанна на IQueryable, который является такой специализированной монадой списка для БД, и без которого я думаю ситуация с ORM в сишарпе была бы куда печальнее. Именно подобные абстракции дают возможность творить по-настоящему мощные библитеки, и если даже на единственной монаде списка мы можем делать такое, то чего мы можем достичь с их совокупной мощью? А если мы еще и комбинировать их будем?

И именно благодаря им появляется возможность вместо сотен строчек кода написать десяток, который просто склеивает уже существующий библиотечный код. И это не обязательно код от высоколобых математиков из стандартной библиотеки Haskell, это может быть и ваш собственный My.Big.Corporation.Utils, который решает вашу конкретную практическую проблему, но решение которой чуть сложнее чем «отнаследовались от пары базовых классов и порядок». И дело не в том, что задача такая простая, что её может решить даже библиотечный код, а библиотечный код настолько абстрактный, что без проблем сможет помочь вам в вашей сложнейшей бизнес-логике.

Заметка об абстрактности
Хотел заметить, что абстрактный — не значит сложный, а скорее наоборот. Как известно — любую проблему в программировании можно решить еще одним уровнем абстракции, кроме слишком большого количества уровней абстракции. Поэтому, когда я говорю «смотрите какая абстрактная мощь», я говорю про то, что эта мощь позволяет просто рассуждать о сложных процессах, а не просто никому не нужная акробатика на типах. Абстракции — упрощают программирование, а не усложняют.

Да, нужно изучить, какие бывают тайпклассы и что они умеют, хотя не так уж это и страшно: мы в статье рассмотрели где-то треть основных. Но потом этим знанием можно пользоваться до конца жизни. Посмотрите на объем документации Akka, там её действительно очень много. Но теперь спросите у людей, которые на ней пишут — хотели бы они сами с нуля реализовывать весь функционал, который в ней есть? Да, верю, что многие разработчики пожурят что они-то дескать лучше бы сами все сделали, и было бы их решение простое, красивое, да еще и производительное как у гугла. Но вот только велика вероятность что они лукавят, и если у них на проекте используется и персистентность, и автобалансировка акторов, и гарантированная доставка, и какие-нибудь другие нетривиальны фичи, то куда проще разобраться один раз в документации и настроить всю машинерию, чем сделать что-то подобное с нуля. Потому что умные люди написали удобную абстракцию, и работать с ней куда проще, чем делать такое самому. Это правда, что чем сложнее система типов, тем более инопланетную фигню можно навертеть, но так же верно и то, что некоторые вещи просто невозможно сделать удобно в более слабых системах типов.

Поэтому я считаю, что будущее именно за мощными языками, позволяющими делать удобные библиотеки, а не за кодом, который быстро написал — быстро выбросил и сделал новый. Такой подход работает, да, но по-моему опыту на проектах не больше пары сотен строк кода, как только их стало больше — лучше с библиотеками, которые кто-то написал, и хорошо бы, чтобы они были достаточно абстрактными и удобными, чтобы их можно было взять и использовать. Плюс монады — вещь стандартизованная, с простым интерфейсом, и что немаловажно — предсказуемыми свойствами, а гениальные архитектурные решения в каждой компании — свои уникальные, и последствия от их использования бывают самые разные.

Выразительность

Тайпкласс монады позволяет очень четко выражать намерения в коде. К слову, пример того, как хорошо дружит ООП с ФП: монады позволяют удобно и красиво следовать четвертому принципу SOLID. Каким образом? А таким, что код, написанный с использованием монад, выглядит подобным образом:

public M GetArticleComment(int articleId) where M : MonadWriter, MonadReader, MonadHttp

Где MonadWriter/MonadReader/MonadHttp — это те самые сегрегированные по принципу SOLID интерфейсы, каждый из которых отвечает за свой маленький аспект. То есть наша функция говорит о том, что ей нужно уметь писать логи (при этом только в формате LogMessage!), читать конфиг (но только Config!) и ходить по Http (но только на AllowedSite!), и используя всё это она в качестве результата вернет комментарий.

Возможно, это выглядит немного чужеродно, но концепт на самом деле очень простой. Мы делаем это сотни раз, когда после авейта возвращаем значение, а оно завернуто в Task. Мы пишем return 10, тогда как возвращаемое значение Task.

Тут ровно та же история, только вместо Task может быть любая монада M, а соотвественно действием — любой эффект, а не только асинхронный запрос.

Причем, таким образом с монадами мы одновременно следуем и последней букве SOLID, решая одну из самых больших головных болей в ООП разработке — инверсию зависимостей. Нам не нужны гигантские Autofac/Windsor/Ninject/… которые падают в рантайме «нишмагла найти зависимость», вы просто описываете в обычных where условиях нужный функционал, и если вы забыли передать зависимость, то компилятор вам об этом напомнит. Вам не нужна магия, внешняя по отношению к языку, вы просто пишете на сишарпе, а компилятор вам поможет.

Тестируемость

Частично связанное с предыдущим пунктом, абстрагированность от некоторых особенностей логики вроде того, является ли функция асинхронной, позволяет избавиться от моков.

Один из примеров, как ФП
© Habrahabr.ru