Молчание — золото: доказательство существования Гамильтонова цикла в графе
Ульям Гамильтон придумал множество игр, одна из них — задача «кругосветного путешествия» по додекаэдру. В ней вершины додекаэдра носили названия известных городов, а рёбрами были соединяющие их дороги. Игрок должен был совершить путешествие «вокруг света», найдя дорогу, которая проходит через все вершины ровно один раз.
Заменив такую сложную конструкцию плоским графом, изоморфным исходному, получим задачу, которую далее рассмотрим в системе протоколов с нулевым разглашением.
Доказательство с нулевым разглашением
Пусть существует некоторая теорема и две стороны — доказывающая и проверяющая. Первой стороне необходимо убедить вторую в истинности данного утверждения, не открывая при этом никакой другой информации. Таким образом, можно сказать, что передается «нулевое знание» фактического доказательства теоремы.
Очень убедительное (но не абсолютно определенное) свидетельство, что теорема верна, и что доказывающий знает это самое доказательство, дает интерактивный вероятностный протокол, называющийся доказательством с нулевым разглашением.
Интерактивность в данном определении говорит о том, что стороны общаются в течение нескольких раундов. В стандартных математических доказательствах имеет место только один вид взаимодействия: доказывающий дает проверяющему доказательство «на проверку», и на этом все заканчивается. В нашем же случае процесс доказательства утверждения превращается в разговор, который заканчивается убеждением проверяющего (если все идет хорошо).
Доказательства с нулевым разглашением не являются доказательствами в математическомсмысле этого термина, потому что есть некоторая небольшая вероятность, что обманом доказывающий сможет убедить проверяющего в ложном утверждении, хотя она и будет приближаться к 0 по мере увеличения числа этапов взаимодействия. С другой стороны, протокол абсолютно -, а не только вероятно — гарантирует доказывающему, что проверяющему не разглашается ни намека на доказательство.
Как убедить кого-то в существовании Гамильтонова цикла, не раскрывая сам цикл
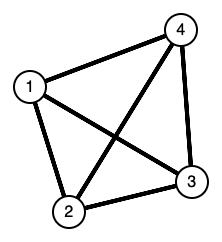
Пусть обеим сторонам известен некоторый граф 
, вершины которого пронумерованы от 
до 
. Необходимо доказать проверяющему существование цикла в G, который посещает каждую вершину ровно один раз.
На вход системе с нулевым разглашением мы подаем
, где 
— положительное целое число, которое играет роль параметра безопасности и является количеством последовательных взаимодействий между сторонами: чем больше 
, тем больше уверенность проверяющего в доказательстве.
Дальнейшие шаги будут выполняться
раз.
Доказывающая сторона выбирает случайную перестановку чисел 
и рисует матрицу смежности для графа, помечая строки и столбцы в соответствии с этой перестановкой. Получается новый граф, изоморфный исходному, построенный по данной матрице, если бы нумерация строк и столбцов у нее шла в естественном порядке.
Проще говоря, мы шифруем исходный граф в изоморфный ему.
Приватное состояние матрицы, доступное только доказывающей стороне.
Публичное состояние матрицы, известное обеим сторонам.
Проверяющая сторона получает скрытую матрицу и делает выбор:
Попросить доказывающую сторону открыть
сетки, соответствующих краям цикла Гамильтона. Процесс раскрытия симметричен: если показана запись 
в матрице, доказывающая сторона должна также показать запись
.C другой стороны, можно попросить доказывающую сторону открыть граф целиком.
Результат для проверяющей стороны в первом случае будет выглядеть, например, так:
Наличие 1 во всех открытых квадратах доказывает существование цикла Гамильтона в графе.
Если у проверяющего была бы возможность задавать только первый вопрос, доказывающий мог бы его легко обмануть, и, не зная Гамильтонова цикла исходного графа G, мог бы подменить его на другой с тем же количеством вершин, в котором сам знал бы цикл. Короче говоря, проверяющий благодаря второму вопросу, хочет убедиться в том, что рассматриваемый граф действительно изоморфен исходному.
Выбор того, что проверяющий будет просить у доказывающего, на каждом шаге определяется «подбрасыванием монетки».
В итоге проверяющая сторона либо поверит доказательству, либо отклонит его.
Почему это — нулевое знание?
Докажем, что проверяющая сторона, благодаря разговору, не может получить никакой «лишней» информации.
Может показаться, что ответ на первый вопрос предоставляет проверяющему знание, благодаря которому он способен самостоятельно полностью узнать доказательство.
Это было бы верно, если бы он знал перестановку вершин, переводящую шифрованный графв исходный, но поскольку вопросы задаются по одному, и каждый раз изоморфная копия G меняется, то найти перестановку — дело безнадёжное — это значило бы решить проблему изоморфизма графов.
С другой стороны, ответ на второй вопрос, очевидно, не даст проверяющему никакой информации, так как, он получает изоморфную копию графа G , но мог бы и самостоятельно построить их сколько угодно, переставляя вершины исходного графа.
Что и требовалось доказать.
Заключение
Рассмотрим задачу идентификации личности. Если решать ее простым использованием пароля, то гарантия того, что он не попадет в руки злоумышленников, не очень велика. Поэтому на арену врывается протокол, описанный выше, работая по принципу «я знаю только половину информации».
Конечно, при таком условии нельзя быть абсолютно уверенным в том, что идентификация личности будет стопроцентной. Но проверяющий каждый раз может спросить любую часть информации, причём несколько раз. К тому же, можно использовать при этом Гамильтоновы циклы, получая очень надёжную систему доступа.
Материал подготовлен при использовании литературы:
Manuel Blum «How to Prove a Theorem So No One Else Can Claim It»
Шнайер Б. Прикладная криптография, 2-е издание: протоколы, алгоритмы, исходные тексты на языке Си //Под редакцией ПВ Семьянова. М., Триумф. — 2002.
