Моделирование физических процессов на примере гидропривода в SimInTech
В предыдущей статье (Конечные автоматы в SimInTech), было показано как создавать модель системы управления на основе конечных автоматов и получать из нее код Си, готовый для загрузки в контроллер. В качестве объекта управления была выбрана достаточно простая система нагреватель и была создана примитивная модель. Чем сложнее модель, объекта тем сложнее система управления и тем интереснее ее моделирования на стадии разработки.
Основное назначение данного текста — показать как создавать модели в ПО SimInTech, зная математические уравнения физических процессов. В качестве примера использовались уравнения физических процессов в гидроприводе. По аналогии так же можно решать задачу с другими физическими процессами, уравнения которых нам известны.
За основу, с любезного разрешения автора, было взято вот это методическое пособие: Андреев М.А. Математическое моделирование гидропривода: Учебное пособие. — на правах рукописи, 2017. — 61 с.
Оригинал расположен здесь: vk.com/doc2869_441829149
С автором оригинального руководства можно связаться по контактам
ВКонтакте: vk.com/max.andreev
Facebook: www.facebook.com/max.andreev
Telegram: t.me/MaximAndreev
Предисловие от Максима Андреева:
С программой SimInTech я столкнулся будучи студентом ещё в те времена, когда она называлась «МВТУ» (Моделирование В Технических Устройствах). Так что, свои первые неловкие попытки моделировать гидропривод я предпринимал именно в ней. Скажу честно, что после того как у меня появилась возможность работать в MATLAB Simulink, я постарался забыть об этом опыте как о страшном сне (впрочем, после пары лет работы в программе SimulationX я и об опыте моделирования в Simulink (включая Simscape) предпочитаю лишний раз не вспоминать).
Тем не менее, мои глубинные патриотические чувства не может не трогать тот факт, что команда разработчиков в последние годы активно принялась за совершенствование этого важного для отечественной инженерной отрасли наследия советских инженеров и существенно продвинулась в этом деле (об этом говорит хотя бы то, что модели, созданные в SimInTech, используются для моделирования работы АЭС, в т.ч. и в Германии). Поэтому, когда ко мне обратились за разрешением адаптировать текст моего учебного пособия для SimInTech, я конечно же согласился.
Введение
В советское время было написано достаточно много литературы, посвященной расчету гидропривода, в том числе описанию физических процессов и математическому моделированию. Но проблема заключается в том, что для того, чтобы эти книги принесли пользу читателю, необходимо уже уметь писать математические модели. По крайней мере мне нигде не удалось найти описания пошагового процесса создания математической̆ модели гидропривода. В лучшем случае автор подробно описывает откуда берётся каждое уравнение огромной системы, но что с ними дальше делать, обычно не очень понятно.
Здесь я постараюсь изложить общую методологию создания математической модели гидропривода различной сложности, начиная от расчетной схемы, записи уравнений и заканчивая реализацией в SimInTech, демонстрационную версию которой можно получить здесь.
После прочтения этого руководства вы будете в состоянии самостоятельно, без использования каких-либо шаблонов, смоделировать работу гидропривода с учетом основных физических процессов и понимать специальную литературу, из которой сможете опять-таки самостоятельно почерпнуть способы описания более сложных процессов.
Принципы создания моделей гидропривода можно применять для любых других систем, дифференциальные уравнения которых, вам известны.
От записи уравнений к результату
В освоении любого незнакомого ранее ремесла, очень важно взять посильную тренировочную задачу.
В нашем случае задача будет предельно проста:
Имеется цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, он работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Нужно посмотреть как он будет перемещаться, если мы ступенькой подадим в полость с начальным объемом 20 см3 давление 200 бар. Чтобы плунжер не превратился в пулю, поставим между источником давления и камерой дроссель диаметром 0,2 мм.
С чего же начать? Многим может показаться, что нужно начать с выбора софта, в котором можно моделировать такую систему. Это не так. На самом деле, начать нужно с листа бумаги и карандаша. Если при помощи этих инструментов внимательно записать уравнения, то потом можно будет решить их в любом софте.
Более того, как показывает практика, если посадить человека за какую-нибудь программу, где математические модели можно писать путем перетаскивания готовых блочков из библиотек, чаще всего результат оказывается неудовлетворительным. В лучшем случае модель просто отказывается считаться. В худшем случае она выдает какой-то бредовый результат, но автору уже трудно поверить в то, что проблема не в софте, а в его кривых руках.
Поэтому я убежден, что по крайней мере на начальном этапе просто необходимо прописывать все уравнения. Этим и займёмся.
Первое правило: »Дроби задачи на подзадачи! »
В нашем случае можно выделить несколько физических процессов, поддающихся математическому описанию:
• прохождение рабочей жидкости через дроссель (дросселирование);
• её сжатие в рабочей полости плунжера;
• перемещение массы с учетом взаимодействия с пружиной и демпфером.
Второе правило: »Начинай с конца! »
Что мы хотим получить в итоге? Наверное, график зависимости перемещения плунжера x от времени t. Так давайте и начнем описание с уравнения движения этого плунжера: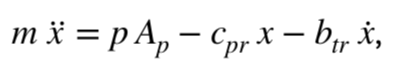 
(1)
где m — масса плунжера, Ap — площадь плунжера, Сpr — жесткость пружины, btr — коэффициент вязкого трения, p — давление в камере.
Здесь нет ничего нового для тех, кто учился хотя бы до 6-го класса школы. Разве что производные заменены точками для удобства. Единственное на что необходимо обратить внимание, это на выбор положительного направления перемещения и на знаки действующих сил.
На рисунке видно, что в качестве положительного направления я выбрал перемещение плунжера вправо. Тогда сила со стороны жидкости в уравнении будет со знаком «плюс», сила со стороны пружины и демпфера со знаком «минус». Вот и всё.
К черту формулы! Даешь моделирование!
Поскольку мы моделируем в SimInTech, то что бы не откладывать в долгий ящик, мы можем начинать создавать модель, в полном соответствии с правилом 1, решаем задачу по частям сначала — плунжер с пружиной.
Открываем SimInTech и создаем новый проект общего вида (Главное меню »Файл/Новый проект/Схема модели общего вида»).
Сначала запишем в качестве констант исходные данные, которые нам нужны для расчета. На схемном окне проекта вызовем редактор скрипта, здесь мы запишем все константы из исходных данных (см. рисунок 1).
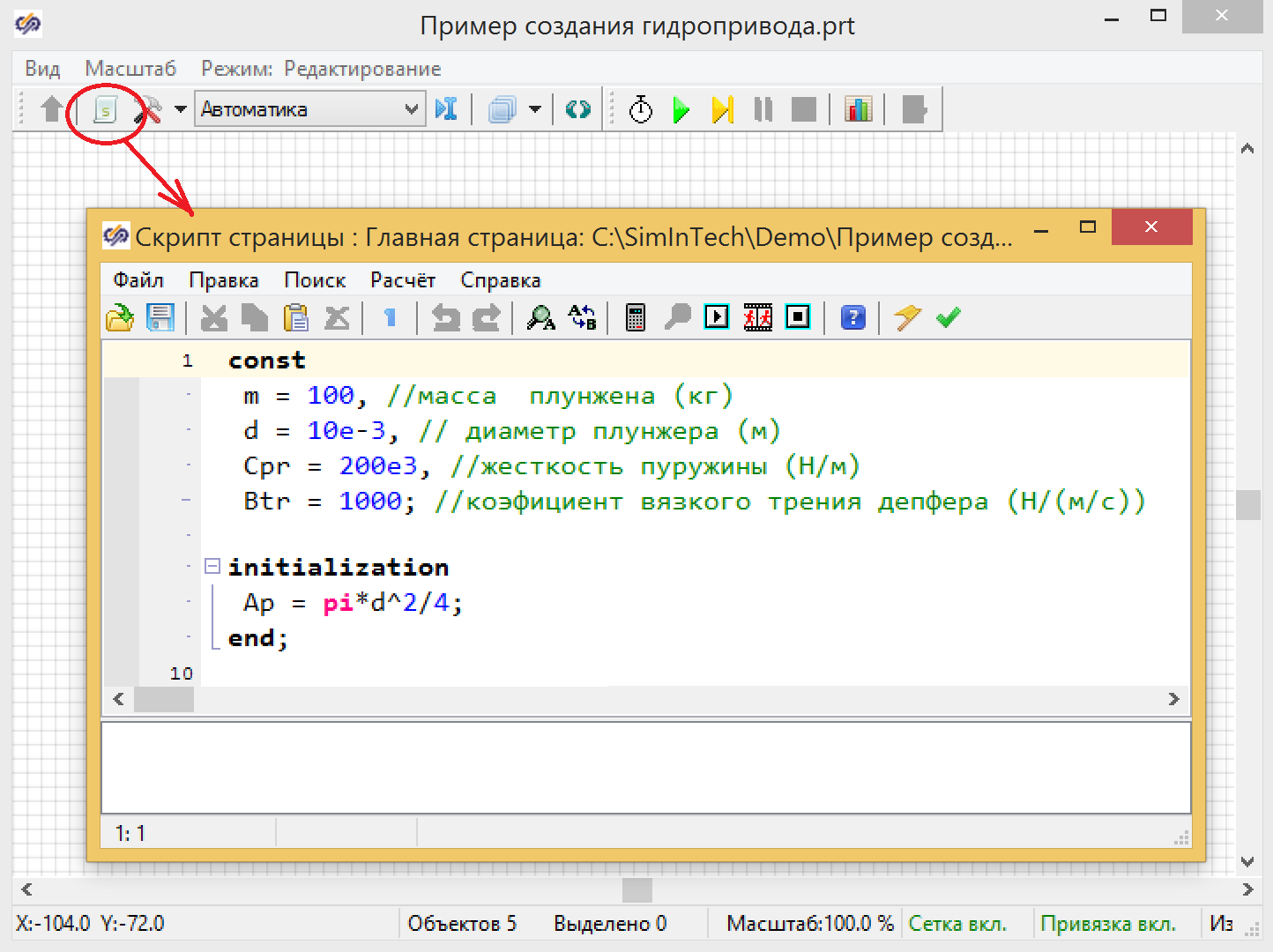
Рисунок 1. Задание глобальных параметров расчета.
Константы задаются через запятую, после последней ставится точка запятой. (см. рис. 1). Для того, чтобы не путаться в дальнейшем, все константы заданы в стандартных единицах измерений.
Так же выполним расчет площади проходного сечения. Площадь мы рассчитываем в секции инициализации, которая выполняется только один раз при старте расчета.
Константы и переменные, заданные в данном окне, доступны в любой части проекта.
Разместим на схеме блоки »Ступенька» из закладки »Источники»,»Язык программирования» из закладки »Динамические» и «График» из закладки »Данные». Схема должна получится сходной с рисунком 2:
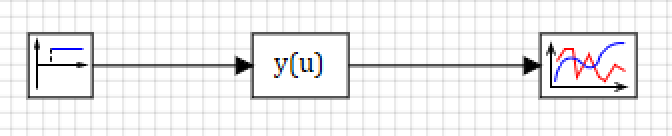
Рисунок 2. Схема модели плунжера.
С помощью блока ступенька будем моделировать входное воздействие, для модели плунжера это давление.
На 1 секунде расчета значение будет меняться с 0 до 200 бар. Для этого в свойствах блока зададим значения, указанные на рисунке 3:
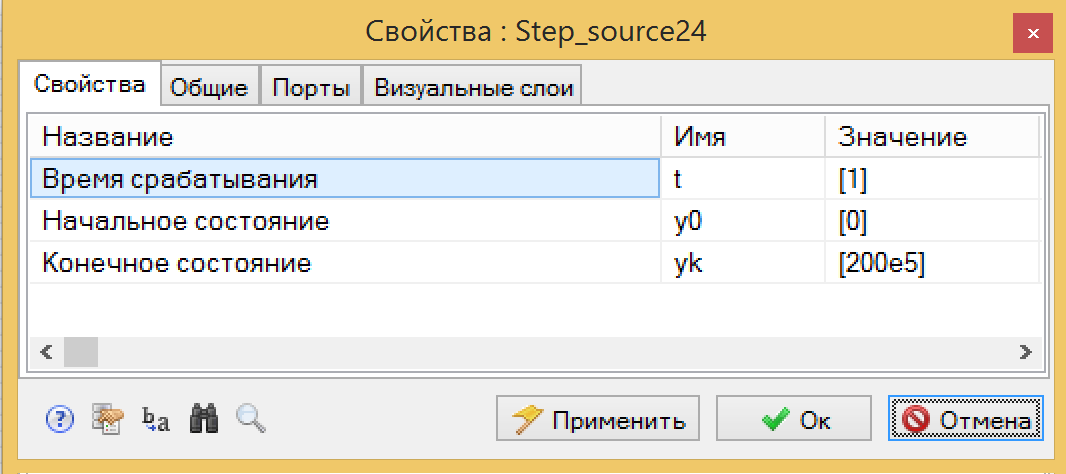
Рисунок 3. Настройки параметров ступеньки.
Если сейчас запустить модель на расчет (кнопка »Пуск»), то график отразит ступеньку исходных данных, блок »Язык программирования», по умолчанию просто передает сигнал без изменений:
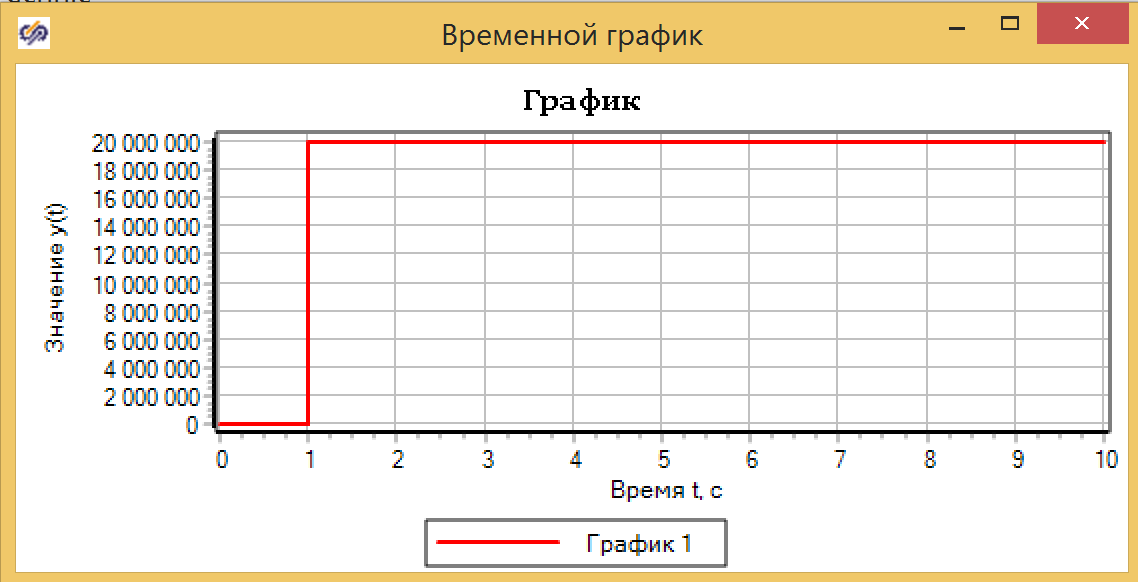
Рисунок 4. График ступеньки.
В блоке «Язык программирования» можно записывать уравнения динамики объекта в форме Коши.
Прежде чем перейти к записи модели преобразуем уравнение (1), в систему двух уравнений, добавив новую переменную — скорость v (t) = dx (t)/dt.
Таким образом, уравнения движения примут вид 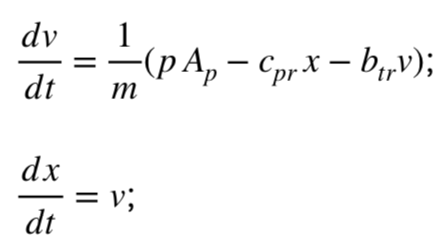2: 
(2)
Из такой системы уже можно создавать модель. Входным параметром модели будет давление p (t), выходным параметром будет перемещение плунжера х (t).
В модели будут две динамические переменные х (t) и v (t), начальные значения этих переменных принимаем равными 0.
Такую систему уже можно записывать на языке программирования, как показано на рисунке 5.
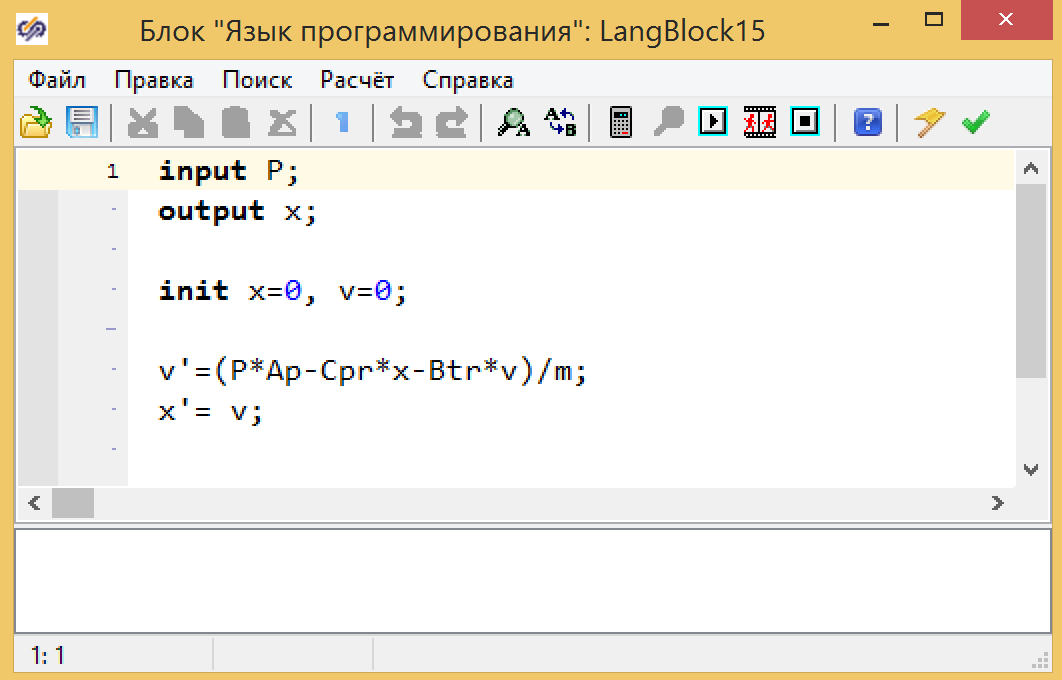
Рисунок 5. Модель плунжера с пружиной
Текст, по моему мнению, максимально понятен практически каждому человеку, кто знаком с любым языком программирования.
input P; — вход в блок (давление)
оutput x; — выхода из блока.
init x=0, v=0; — объявление динамических переменных и присвоение им начальных значений;
Дальше идет текст, который выполняется на каждом шаге моделирования.
В принципе текст на языке программирования практически повторяет систему уравнений, где производные dx (t)/dt и dv (t)/dt обозначены как x» и v».
Если сейчас запустить процесс моделирования, то скорее всего вы получите график как на рисунке 6. Как говорится упс! У нас получилась полная хрень, ни на что не похожая. Данный график наглядно иллюстрирует необходимость соблюдения правила номер раз. «Дроби задачи на подзадачи!»
Поскольку мы решаем уравнение, описывающее движение массы на пружинке, мы приблизительно понимаем, что ожидать. Должен быть колебательный процесс, который из-за наличия силы трения должен затухать. Мы же видим колебания, которые ведут себя очень странно.
Рисунок 6. График перемещения плунжера.
Главное здесь не пугаться и не впадать в панику, таких бессмысленных и беспощадных графиков вы еще насмотритесь. Первое, что рекомендуем сделать — изменить шаг интегрирования. Фактически эта уневерсальная рекомендация явялется третьем правилом моделирования :
Третье правило моделирования: При любых непонятных результатах уменьшай шаг интегрирования!
Нажмите кнопку с молотком и отверткой на схемном окне, найдите в параметрах расчета максимальный шаг моделирования и измените его на 0.01 (см. рис. 7.) Закройте окно настроек нажав кнопку ОК.
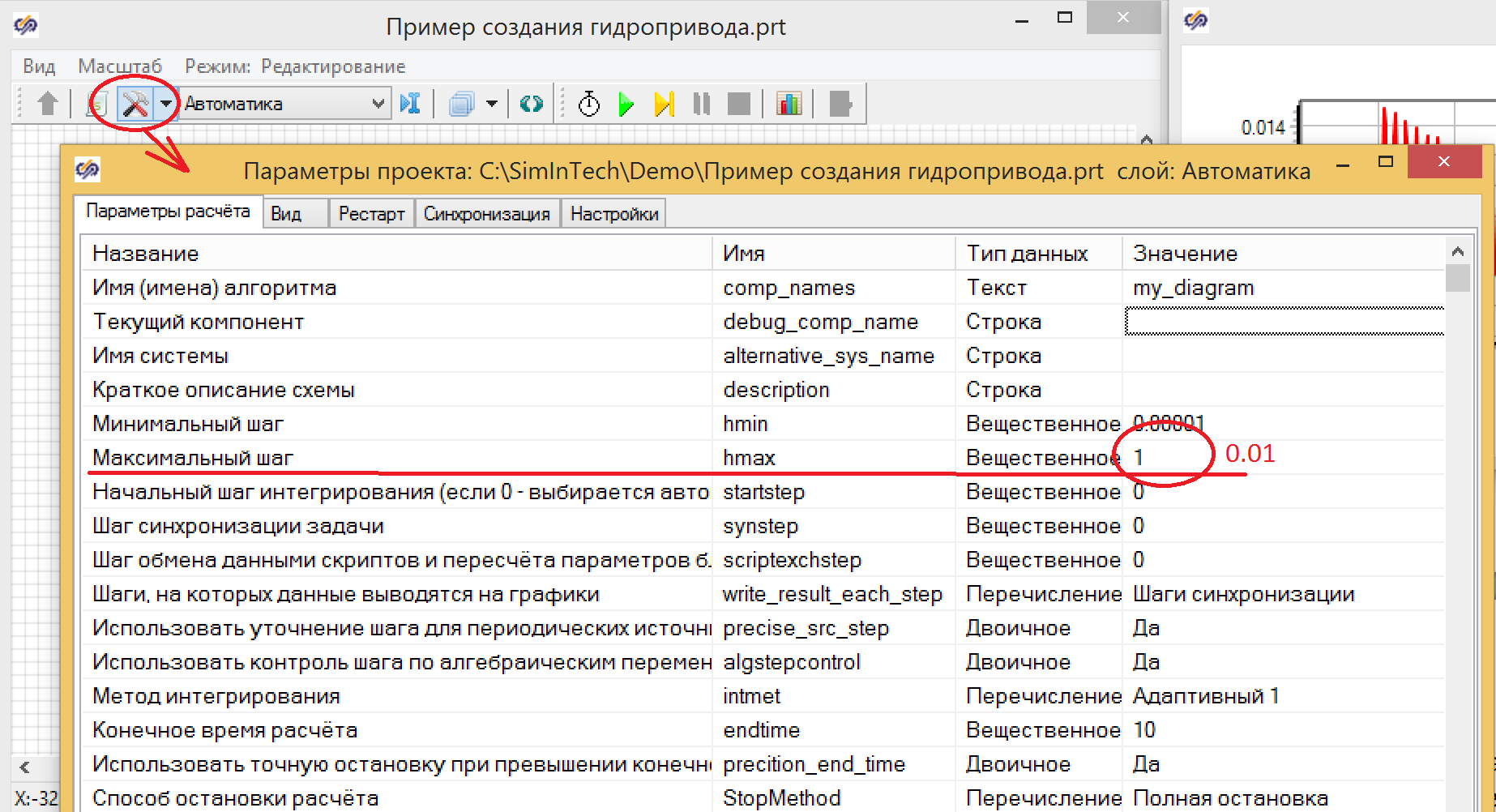
Рисунок 7. Настройка шага интегрирования.
Если запустить расчет с такими настройками (как показано на рисунке 7), то результат буде более похож на правду (см. рис. 8).
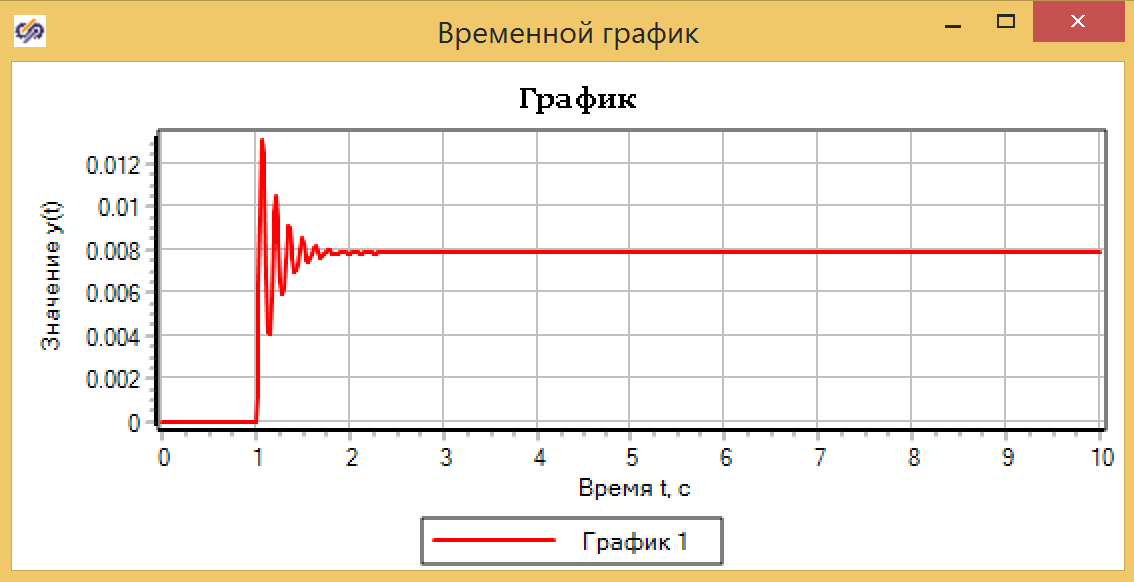
Рисунок 8. Результат при максимальном шаге 0,01.
Результат расчета на рисунке 8 показывает, что у нас в момент возникновения давления на 1 секунде происходит быстрый разгон плунжера, из-за инерции движения, плунжер проскакивает точку равновесия, пружина сжимается и возвращает поршень назад, возникают колебания, а поскольку у нас есть сопротивление трения, то колебания затухающие.
Решение задачи по частям дает возможность нам проверить правильность физического моделирования, путем постановки численного эксперимента.
Например, если уменьшить коэффициент вязкого трения в 10 раз, то колебания должны затухать дольше. Изменим данный параметр в основном скрипте модели (см. рис. 1) и при моделировании получим график как на рисунке 9:
Рисунок 9. Результат при Btr = 100.
Если увеличить массу плунжера в 10 раз, оставляя все остальные параметры заданными изначально, то колебания будут происходит с меньшей частотой, и время переходного процесса так же увеличится, что мы наблюдаем на рисунке 10.
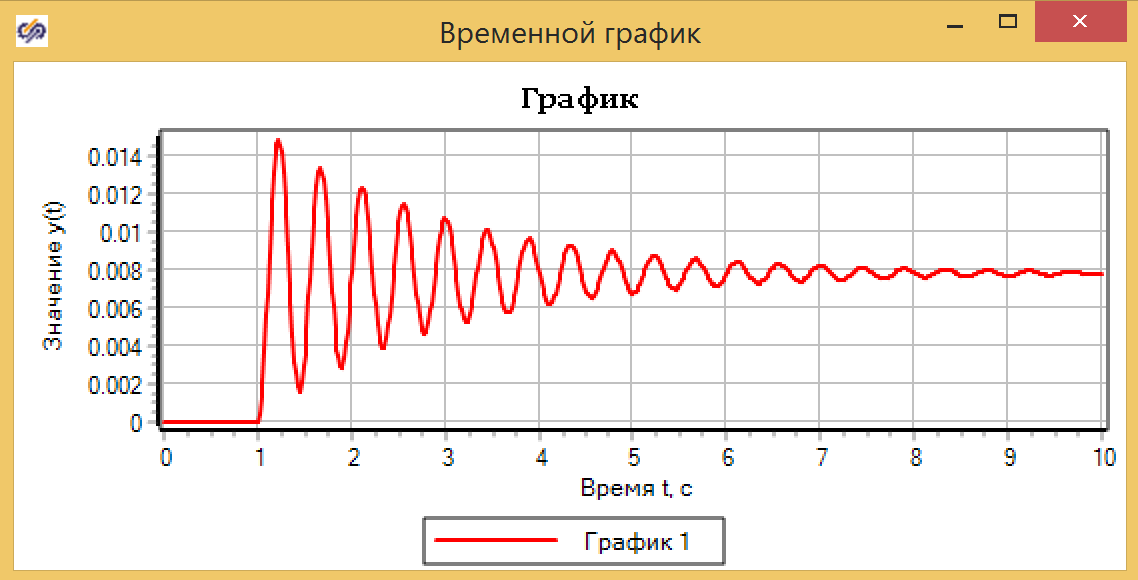
Рисунок 10. Результат при m = 1000.
Еще одним способом проверки правильности модели будет сравнение конечного перемещения, полученного в модели и рассчитанного из условия равновесия системы. В случае равновесия сила, действующая на плунжер (Pst*Ap), уравновешивается силой сжатой пружины (Cpr*x_st), где:
Pst — давление статическое;
x_st — перемещение поршня (сажание пружины);
Pst*Ap = Cpr*x_st или x_st = Pst*Ap/Cpr.
Расчет конечного положения плунжера можно выполнить прямо в окне блока «Язык программирования» (см. Рисунок 11).
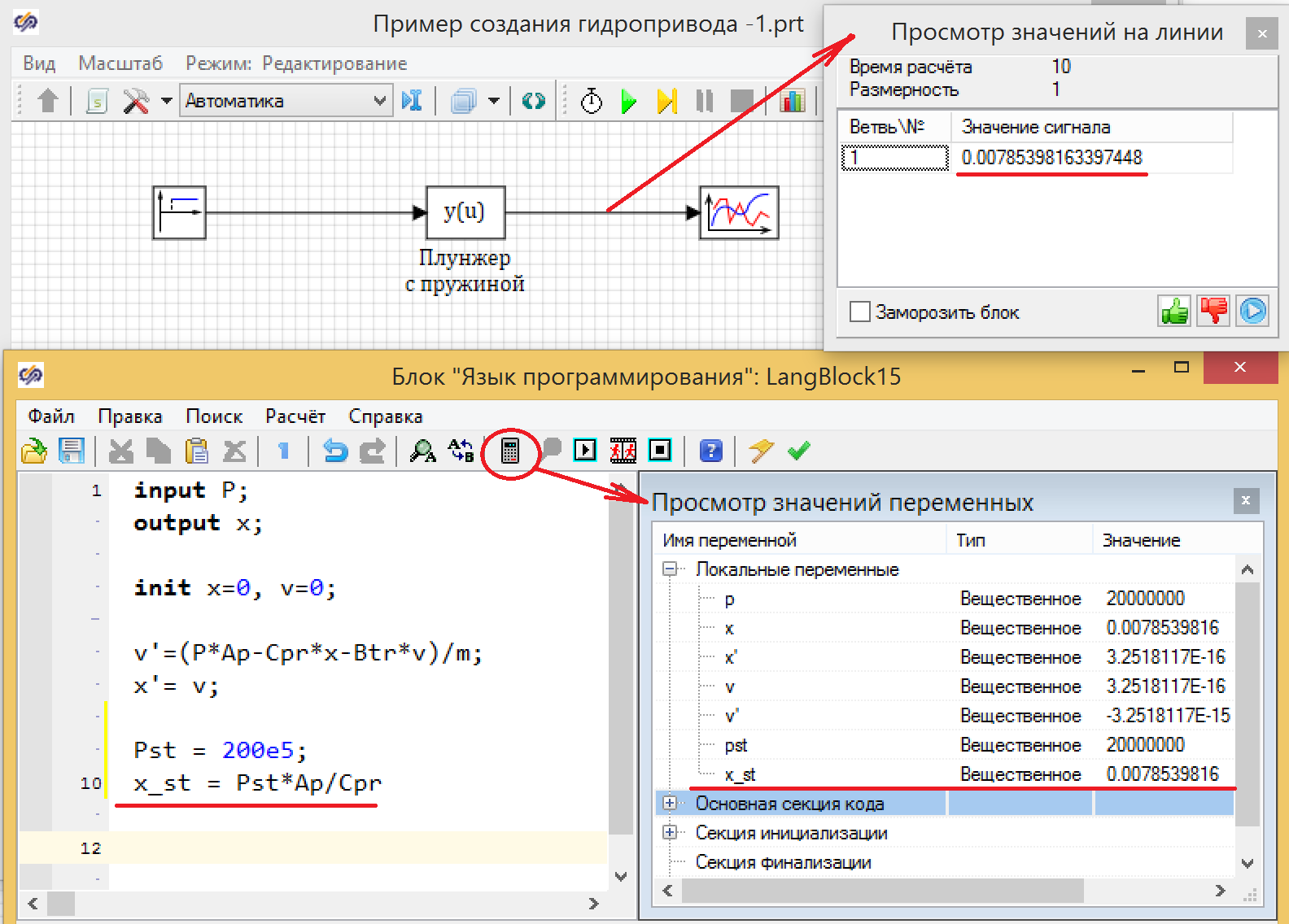
Рисунок 11. Проверка конечного положения плунжера.
Запись расчета стационарного положения можно внести прямо в тело программы блока, и при нажатии на кнопку «калькулятор» будет выведено окно с значениями переменных скрипта, двойной клик по линии связи на выходе из блока покажет значение сигнала на линии связи. Мы убеждаемся, что переходный процесс завершился с таким же значением, как и статический расчет (см. рис 11.) Таким образом можно убедиться, что модель выходит на правильные значения положения и при 150 бар и при 250 бар.
Получив и проверив модель плунжера с пружиной, можно переходить к модели камеры.
Модель камеры
Уже понятно, что входным сигналом для модели плунжера является давление в рабочей камере. Неплохо было бы знать это значение давления в рабочей камере. И тут уже появляется что-то новенькое. Оказывается, то что нам рассказывали в школе и на младших курсах про несжимаемость жидкости — враньё. На самом деле она сжимается, особенно в гидроприводе с давлением от 160 бар и выше.
Да, я знаю, что вы сейчас в глубоком шоке от этой новости, но нужно как-то с этим дальше жить и описывать этот процесс уравнениями. На мой взгляд, удобнее всего это описывается следующим образом:
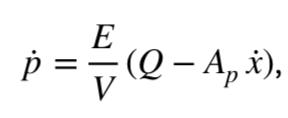(3)
где: ṗ — скорость изменения давления; E — приведенный объемный модуль упругости рабочей жидкости; V — объем сжимаемой рабочей жидкости; Q — расход, поступающий в рабочую камеру; Aр*x' — скорость изменения объема камеры из-за перемещения плунжера
Вывести это выражение нетрудно из формулы для определения объемного модуля упругости:
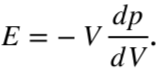(4)
Если разнести дифференциалы давления и объема по разные стороны знака равенства, а затем продифференцировать обе части по времени.
Логично предположить, что давление будет меняться тем быстрее, чем выше модуль упругости рабочей жидкости E, и тем медленнее, чем больше объем этой жидкости V. Поэтому модуль упругости у нас в числителе, а объем — в знаменателе. В скобки я поместил алгебраическую сумму расходов. В данном случае мы имеем дело с расходом через дроссель Q и с геометрическим расходом от перемещения плунжера. Положительное значение расхода Q при прочих равных будет приводить к росту давления (положительная скорость изменения давления), а положительная скорость перемещения плунжера к падению давления. Поэтому расход через дроссель в уравнении со знаком «плюс», а геометрический расход со знаком «минус».
Объем камеры в свою очередь можно описать формулой: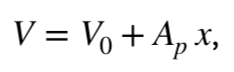 
(5)
Где V0 — т.н. «мертвый» объем (объем жидкости при нулевом положении x (t) поршня).
На самом деле, влияние изменения объема жидкости очень несущественно, и во избежание лишних ошибок (например, при отрицательных x), лучше принимать просто постоянный объём, равный половине разницы объёмов в конечном и начальном положениях.
Ко мне часто приходят студенты, которые не первые сутки бьются над своей моделью, которая выдаёт какой-то бред в виде астрономических значений давления, нереальных перемещений и т.п. Очень часто мне бывает достаточно примерно одной минуты «общения» с моделью, чтобы она заработала. И дело тут не в моей гениальности, а в том, что почему-то около 80% ошибок у начинающих «моделистов» приходятся именно на неправильную расстановку знаков в уравнении баланса расходов (уравнении сжимаемости жидкости). Я не был исключением. Мне, насколько я помню, понадобилась где-то неделя, чтобы найти в своей первой̆ модели гидропривода эту ошибку.
А поскольку у нас модель плунжера в SimInTech уже отлажена, более того, у нас есть возможность проверить положение штока, мы не будем тратить недели на поиск ошибок.
Модель камеры в SimInTech
Вспоминая правило первое, решаем задачу по частям, создаем модель камеры и подключаем ее к уже испытанной и проверенной модели плунжера.
Для создания модели камеры нам в общих константах проекта понадобятся две новые величины
V0 — начальный объем камеры и Е = 13e8 — приведенный объемный модуль упругости, добавим их в нашем главном скрипте программы:
Рисунок 12. Константы в главном скрипте модели.
Обратите внимание на перенос знака «точка с запятой». Все константы разделены запятыми, секция заканчивается «точкой с запятой».
Входными параметрами для расчета является расход жидкости Q, положение поршня x и скорость перемещения v (смотри формулу 3).
Поставьте новый блок типа «Язык программирования» на схему и просто перепишите уравнения 5 и 3.
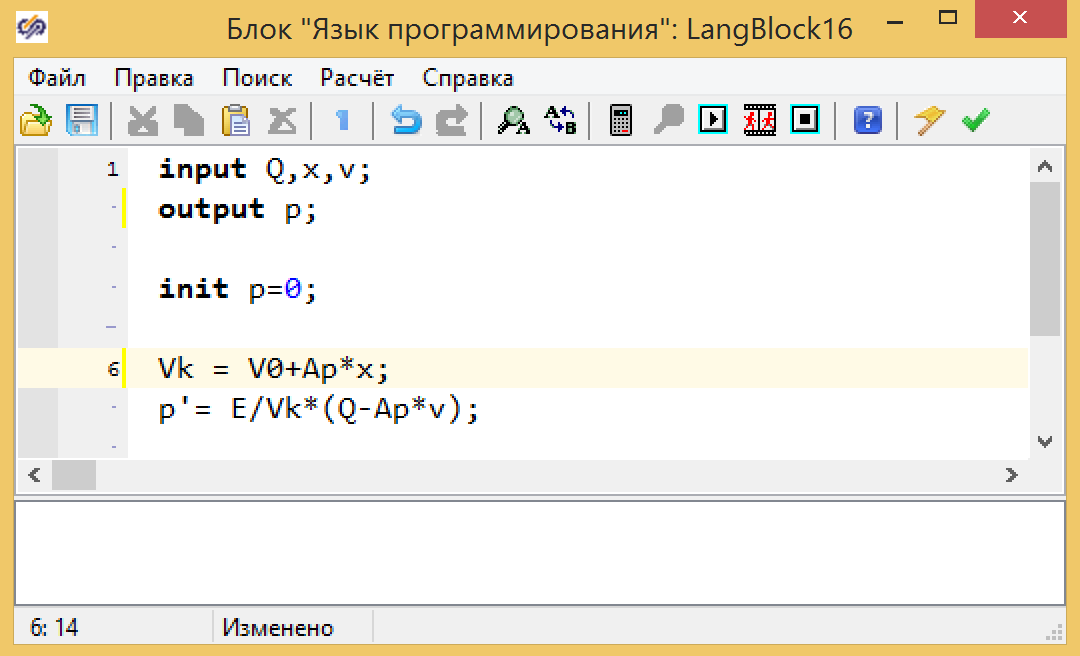
Рисунок 13. Модель камеры цилиндра.
Скорость перемещения плунжера необходимо забрать из блока плунжера с пружиной. Для этого меняем текст модели в готовом блоке, добавив еще один выход (см. рис. 14).
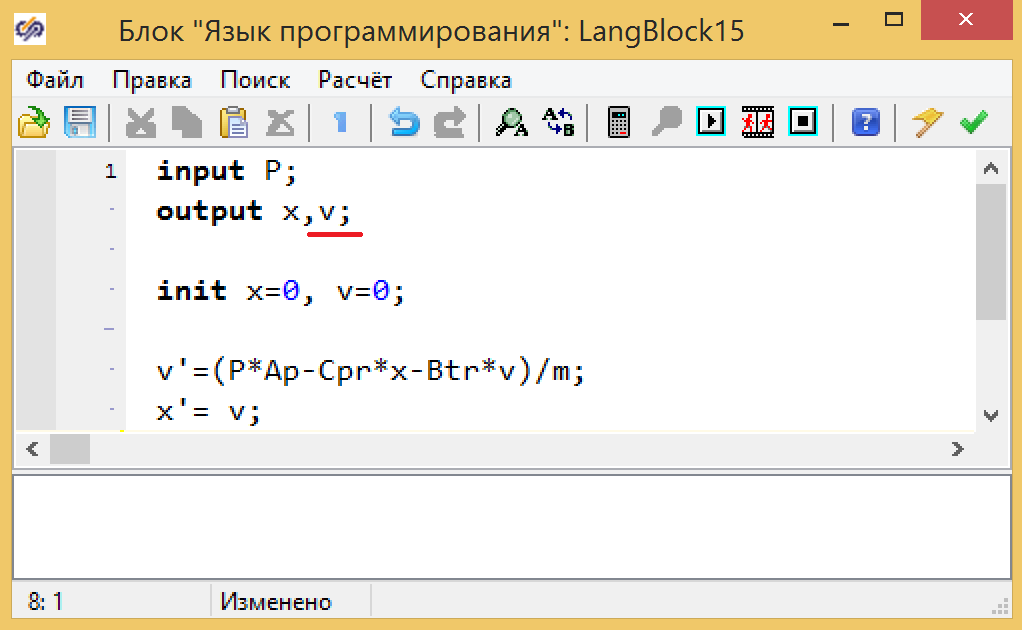
Рисунок 14. Модель плунжера с добавленных выходом — скоростью.
Соединяем схему как показано на рисунке 15, подписываем блоки для наглядности.
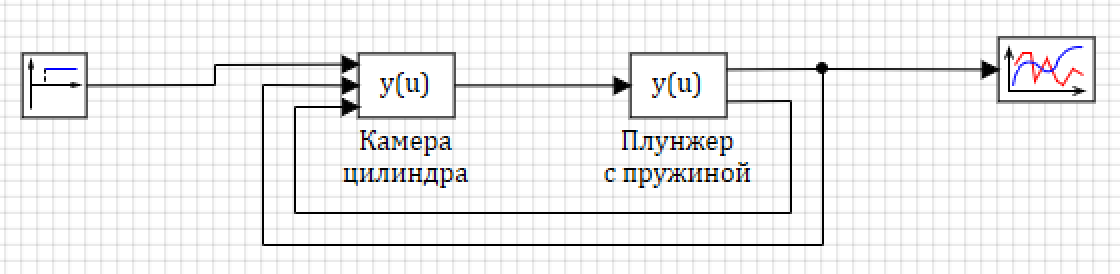
Рисунок 15. Общая модель цилиндра и камеры.
В принципе можно запустить проект на моделирование и получить несуразные астрономические значения перемещения плунжера в тысячи километров.
Но можно включить голову и вспомнить, что на предыдущем этапе мы подавали на вход модели плунжера давления ступенькой с 200е5 Па (200 бар). Теперь нам нужно из этого блока подать такой расход, чтобы в камере сформировалось давление 200 бар.
Если использовать блок ступенька, то в момент его включения начнет подаваться расход, и он будет постоянным в течение всего времени моделирования, а для требуемого повышения давления мы должны подать в камеру расход только на некоторое время, достаточное для создания давления 200 бар, и после этого прекратить подачу.
Поскольку мы сейчас не знаем, сколько нужно закачать жидкости, для создания требуемого давления в 200 бар, мы используем блок »Кусочно-постоянная» из закладки »Источники». В качестве параметров зададим »прикидочные» значения, приведенные на рисунке 16.
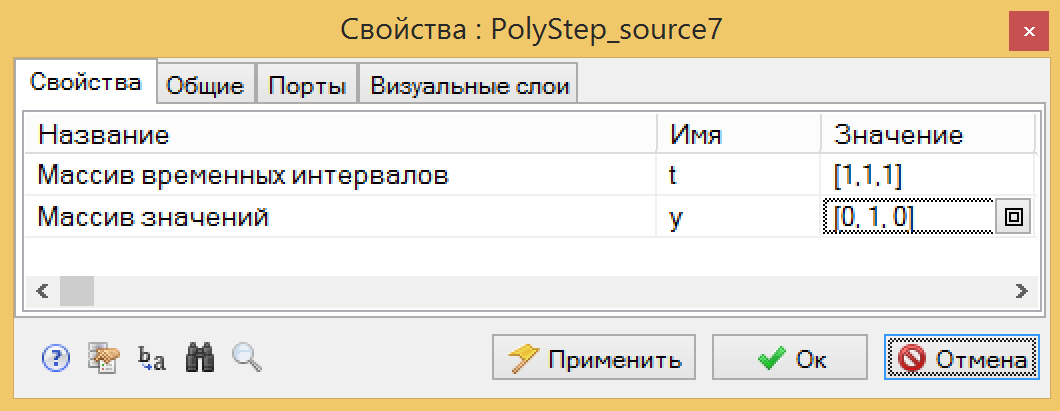
Рисунок 16. Настройки источника расхода в камеру.
В данном блоке задается 3 интервала по 1 секунде. На первом интервале расход 0, на втором интервале расход 1, на следующем и до конца расчета расход 0. Таким образом мы моделируем накачку камеры расходом 1 м^3/c в течение одной секунды. Логично, что такой расход создаст невозможное давление, но мы подберем ее на следующей итерации, сейчас мы просто посмотрим, что у нас получается.
Чтобы понять, насколько мы не угадали с расходом, включим отображение значений на линиях связей (см. рис. 17), что позволит нам видеть, какое давление создано этим объемом жидкости.
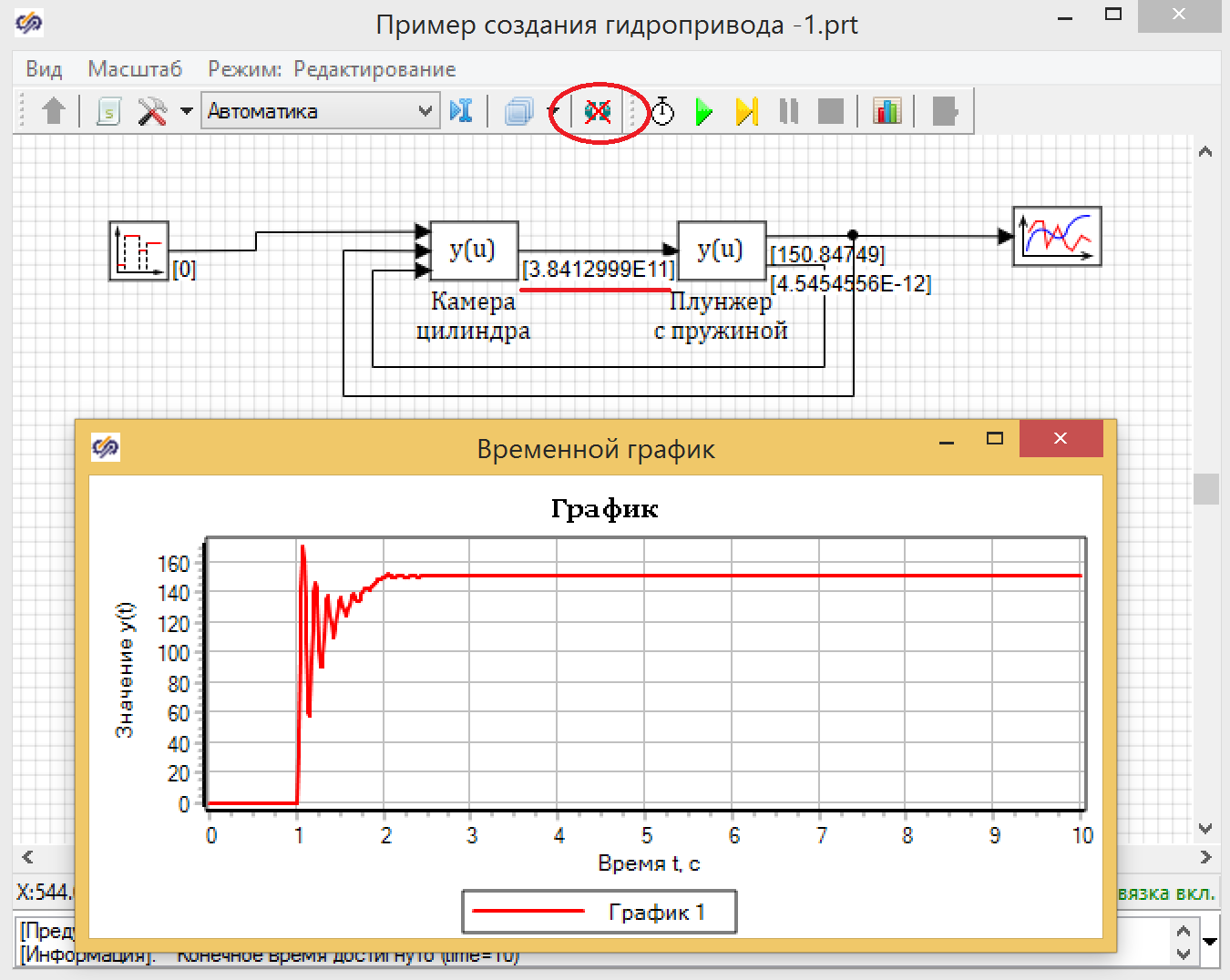
Рисунок 17. Результаты расчета первое приближение.
Результаты расчета показывают, что мы «не угадали» и давление в камере установило на уровень около 3.84 е11 вместо необходимого 200е5 (200 бар).
Путем подбора определяем, что для создания давления в 200 бар необходимый расход должен составлять примерно 0.98e-7 в течение 1 секунды. Результаты моделирования — на рисунке 18
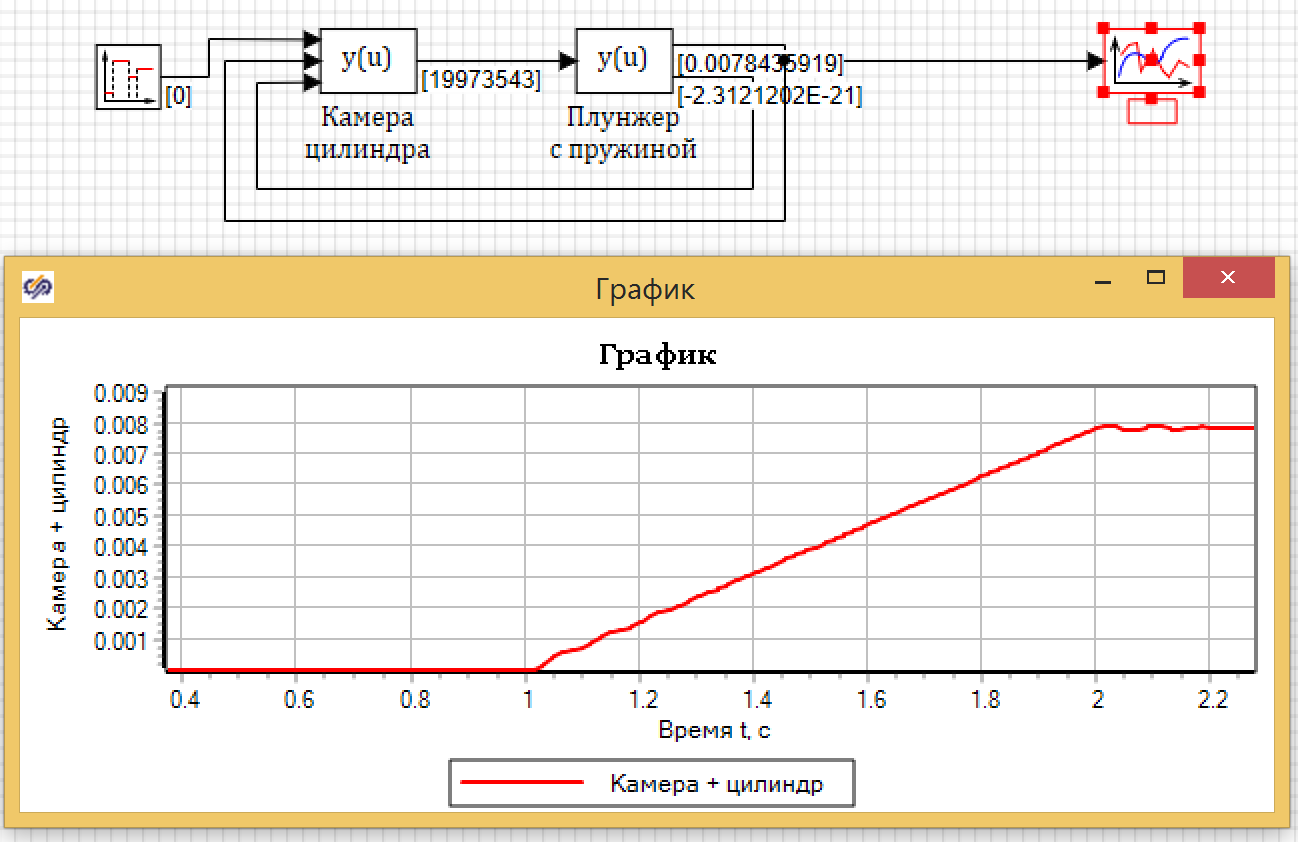
Рисунок 18. Результаты моделирования равномерной подачи в камеру.
На графике видно, что если расход подавать равномерно в течение секунды, то на начальном этапе происходит рост, с колебаниями, затем устанавливается практически равномерный процесс перемещения в течение секунды, пока мы подаем расход в камеру, и затем после 2 секунд остановка с небольшими затухающими колебаниями.
Теперь нам интересно сравнить модель плунжера с пружиной, которую мы создали на первом этапе и ту же модель, но уже подключённую к камере. Поскольку первую модель мы нагружали ударной нагрузкой (ступенькой), то для формирования похожего импульса, необходимо быстро подать в камеру объем, который необходим для создания такого же давления, но за более короткое время. Можно попробовать сократить время импульса, например в 10 раз, и увеличить в 10 раз расход.
Скопируем блок плунжера с пружиной и подадим на него ступеньку 200 бар.
Подадим на вход камеры расход импульсом длительностью 0.1 секунды, подобрав его так, чтобы конечное давление было около 200 бар. Должна получится примерно такая модель как на рисунке 19.
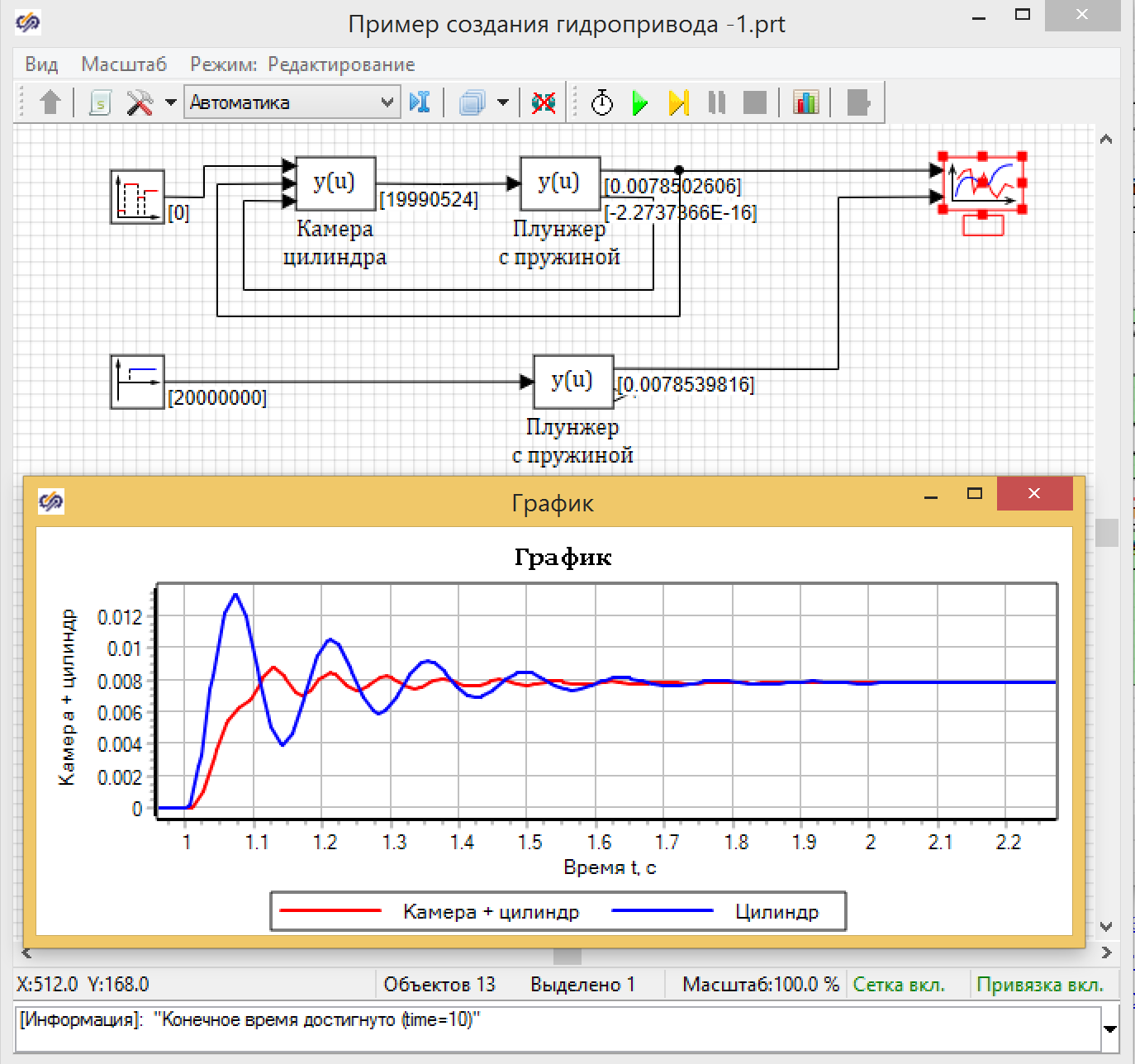
Рисунок 19. Сравнение модели плунжера с камерой и без камеры.
Если посмотреть на графики, видно, что в течении 0,1 секунды пока идет подача расхода в камеру идет перемещение плунжера, которое потом затухает быстрее, чем без камеры (с мгновенным ростом давления), что похоже на правду.
Видно, что у нас положение плунжера примерно соответствует полученному при отдельном моделировании. Таким образом, мы с помощью SimInTech решили еще одну подзадачу.
Остался последний рывок!
Моделирование дросселя.
Ну вот мы и подходим к последнему уравнению, которое описывает расход через дроссель:
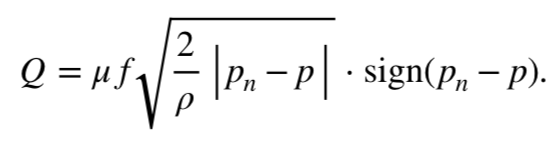(6) где:
- f — площадь сечения дросселя;
- μ — коэффициент расхода;
- pn –давление нагнетания;
- p — давление в камере цилиндра.
В этой формуле тоже нет ничего нового для тех, кто хотя бы пол семестра изучал курс гидравлики. Единственная поправка, которую нужно внести — это учёт теоретической возможности обратного тока рабочей жидкости в случае отрицательной разницы давлений (например, когда на поршень действует сила больше, чем может противопоставить сила со стороны рабочей жидкости). Без этого мы рискуем получить отрицательное подкоренное выражение.
По цифрам: коэффициент расхода μ можно взять равным 0.62, а плотность рабочей жидкости ρ = 850 кг/м^3.
Добавляем новые константы в общий скрипт, который итого принимает вид, представленный на рисунке 20:
Рисунок 20. Список констант проекта.
Расчет проходного сечения дросселя также производим в секции инициализации.
После этого нам остается только записать последнее уравнение 6 в новом блоке «Язык программирования», см. рисунок 21.
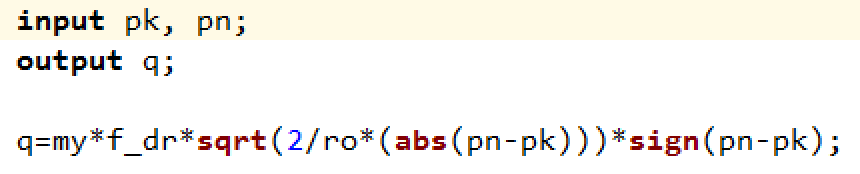
Рисунок 21. Программа блока дроссель.
Обратите внимание, что первым в описании входов записано pk — давление в камере, соответственно вход с этим именем будет сверху, а давление нагнетания — второе, его вход на блоке будет ниже.
После этого можно соединить на схеме: выход расхода соединить с камерой, а на вход нагнетания подать ступеньку с 0 до 200 бар, как мы делали при создании плунжера с пружинкой. Общая схема получится как на рисунке 22.
Там же приведен и результат расчета переходного процесса при увеличении давления нагнетания скачком с 0 до 200 бар
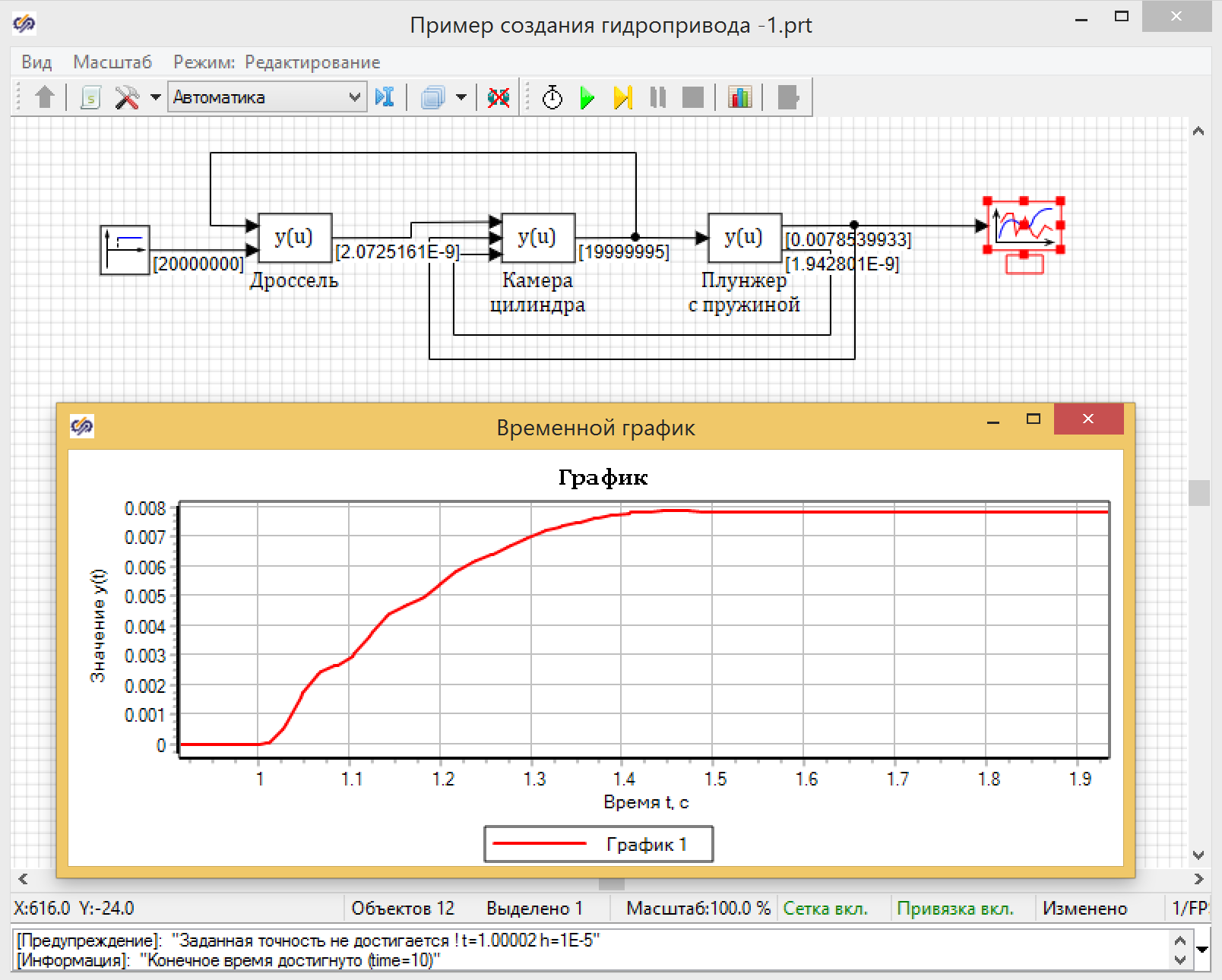
Рисунок 22. Схема моделирования и результат расчета.
Если у вас получился результат как на рис. 22, то поздравляют! Вы только что разработали модель гидропривода в SimInTech. При этом у вас в качестве исходных данных были только диференциальные уравнения.
Теперь по данном образцу и подобию вы можете созать модель для чего угодно, как говорится отмоделировать все что движется и шевелится, а что не движется — подвигать и тоже отмоделировать!
В следующих частях:
- Три варианта представления модели одной и той же модели в SimInTech.
- Сравнение разных моделей гидравлических систем.
- Создание модели реального гидропривода.
