Моделирование движения космических тел08.11.2023 12:45

Давным-давно я прочитал про Демона Лапласа. Это мысленный эксперимент, предложенный французским математиком Пьером-Симоном Лапласом. Суть этого эксперимента в том, что вымышленное существо в определенный момент времени измеряет положение и скорость каждой частицы во Вселенной и таким образом может рассчитать положение любой частицы в любой момент времени: и в будущем, и в прошлом. То есть такое существо смогло бы узнать все, что когда-либо происходило во Вселенной и будет происходить.

Нетрудно догадаться, что такое существо (или машина) невозможно по нескольким причинам. Во-первых, предсказания существа влияют на будущее (например, на мысли этого существа) и существо в каждом своем предсказании должно было бы учитывать влияние результата предсказания на будущее, потом снова влияние нового предсказания на будущее и т.д. Получилась бы своего рода бесконечная рекурсия. Во-вторых, существует принцип неопределенности, согласно которому при повышении точности измерения одной характеристики (в данном случае скорости или положения) точность измерения другой падает. То есть существо не смогло бы достаточно точно измерить положения и скорости частиц, тем самым сделав ошибку предсказания ощутимой. И в-третьих, каким образом возможно измерить положение и скорость всех частиц во Вселенной?

Но ничто не мешает нам создать «упрощенного» Демона Лапласа. Если мы возьмем систему тел, которую можно считать «почти замкнутой» (например, Солнечная система), и определим положение и скорость не каждой частицы (что мы сделать не сможем), а выделим какие-то группы частиц, которые можно объединить в одно тело (планету) и будем рассчитывать положения исходя из этих тел, то получим приемлемую точность, в зависимости от задачи.

Таким вот образом мы будем моделировать движение небесных тел.

Часть 1. Бэкэнд

Переходим к разработке программы. Принцип работы программы довольно прост: мы разбиваем путь тела на много маленьких отрезков (каждый из которых тело проходит за T секунд), на котором считаем ускорение постоянным. Чем меньше будет величина T, тем меньше будут эти отрезки, и тем точнее получится итоговая траектория. С графикой особо напрягаться не будем и используем pygame.

Из физики нам понадобится только одна формула: $F = G \cdot \frac{m_{1} \cdot m_{2}}{r^2}{}$ . Закон всемирного тяготения.

У нас будет набор параметров, куда положим гравитационную постоянную, единичный промежуток времени и масштаб изображения в метрах на пиксель. Пригодится он нам позже.

params = {
    "G" : 6.6743E-11,
    "T" : 3600,
    "scale" : 6E+8
}

В программе будет 2 класса: класс всей системы и класс отдельного тела. При каждой итерации объект класса системы будет вызывать функцию итерации у каждого тела в этой системе, передавая туда параметры. Переходим к написанию класса тела:

class Body:
    def __init__(self, m, x, y, vx, vy, R, color='red'):
        self.m = m # масса тела в кг
        self.x = x # начальная координата в м
        self.y = y # начальная координата в м
        self.vx = vx # начальная скорость по x в м/с
        self.vy = vy # начальная скорость по y в м/с
        self.R = R # радиус круга pygame в пикселях
        self.color = color # цвет тела
        self.ax = self.ay = 0 # инициализируем ускорения сил, действующих на тело

Теперь пишем функцию итерации в классе. Для этого нам нужно разложить по осям силу тяготения:

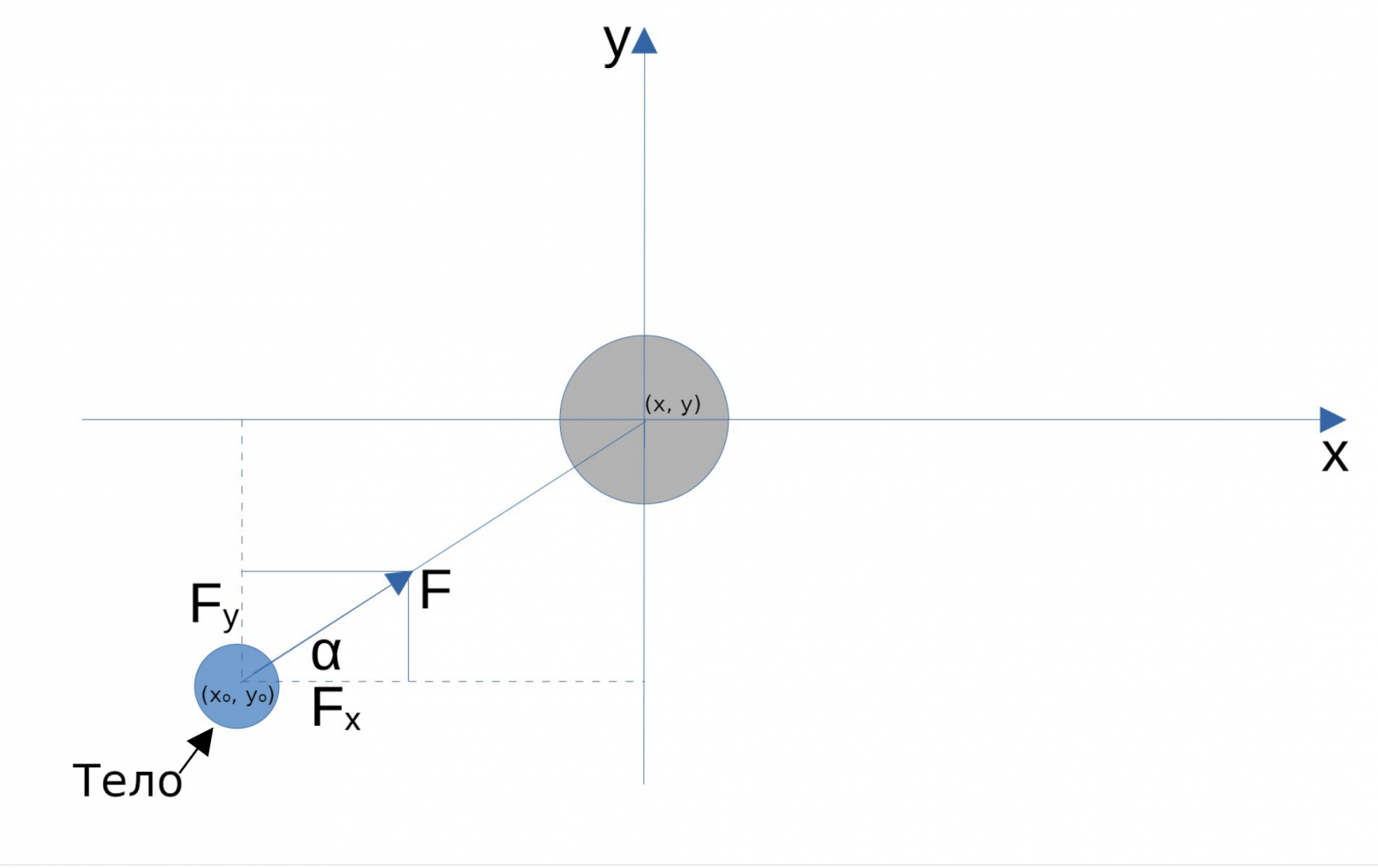
Немного поколдовав с Законом всемирного тяготения и Вторым законом Ньютона получаем:

В формуле x_o, y_o это координаты тела, для которого мы ищем ускорение. А x, y — координаты тела, которое на него действует.

Функция итерации тела будет принимать параметры нашей системы (T, G) и list из всех объектов, кроме текущего, далее высчитывать суммарные ускорения сил, действующих на тело и раскладывать по осям. Нам понадобится модуль math.

def iterate(self, objects, params):
    self.ax = self.ay = 0 #обнуляем ускорение для пересчета
    G = params['G']
    T = params['T']
    # считаем ускорение от всех сил
    for obj in objects:
        self.ax += G * obj.m * (obj.x - self.x) / math.sqrt((obj.x - self.x)**2 + (obj.y - self.y)**2)**3
        self.ay += G * obj.m * (obj.y - self.y) / math.sqrt((obj.x - self.x)**2 + (obj.y - self.y)**2)**3
        
    self.x += self.vx * T + self.ax * T**2 / 2 # по формуле равноускоренного движения считаем новую координату
    self.y += self.vy * T + self.ay * T**2 / 2

    self.vx += self.ax * T # считаем новую скорость в конце отрезка
    self.vy += self.ay * T

Полный код программы на данный момент:

import pygame
import math

class Body:
    def __init__(self, m, x, y, vx, vy, R, color='red'):
        self.m = m # масса тела в кг
        self.x = x # начальная координата в м
        self.y = y # начальная координата в м
        self.vx = vx # начальная скорость по x в м/с
        self.vy = vy # начальная скорость по y в м/с
        self.R = R # радиус круга pygame в пикселях
        self.color = color # цвет тела
        self.ax = self.ay = 0 # инициализируем ускорения сил, действующих на тело

    def iterate(self, objects, params):
        self.ax = self.ay = 0 #обнуляем ускорение для пересчета
        G = params['G']
        T = params['T']
        # считаем ускорение от всех сил
        for obj in objects:
            self.ax += G * obj.m * (obj.x - self.x) / math.sqrt((obj.x - self.x)**2 + (obj.y - self.y)**2)**3
            self.ay += G * obj.m * (obj.y - self.y) / math.sqrt((obj.x - self.x)**2 + (obj.y - self.y)**2)**3
        
        self.x += self.vx * T + self.ax * T**2 / 2 # по формуле равноускоренного движения считаем новую координату
        self.y += self.vy * T + self.ay * T**2 / 2

        self.vx += self.ax * T # считаем новую скорость в конце отрезка
        self.vy += self.ay * T

Теперь переходим к классу системы.

class System:
    def __init__(self, objects, params):
        self.objects = objects
        self.params = params
        self.t = 0 # счетчик прошедшего времени

    def iterate(self):
        for i in range(len(self.objects)):
            obj = self.objects[i]
            obj.iterate(self.objects[:i] + self.objects[i+1:], self.params) # вызывается функция итерации, и в качестве аргумента передаются все объекты, кроме текущего
        self.t += self.params['T']

Вычислительная часть закончена, переходим дальше.

Часть 2. Графика

Сейчас мы настроим pygame, создадим объект класса системы, добавим туда несколько тел и будем в цикле pygame отрисовывать кружок с заданным радиусом, цветом и координатами, после чего вызывать функцию итерации системы.

Только еще нужно немного повозиться с конвертацией координат для отображения на экране. Для этого у нас есть масштаб, а также не забываем, что направление оси y в pygame противоположно (да и начало координат в левом верхнем углу, а нам нужно в центре). Еще pygame автоматически преобразует float в int, поэтому используем округление.

def convert(point, scale, DISPLAY): 
    return (round(point[0] / scale + DISPLAY[0]/2.0), round(-point[1] / scale + DISPLAY[1] / 2.0))

Теперь переходим к pygame. Для ускорения работы программы мы можем сделать 2 вещи: либо увеличить временной промежуток T, что уменьшит точность, либо отрисовывать не каждый кадр, а только каждый n-ый, что мы и сделаем. И если вы не хотите, чтобы fps зависело напрямую от скорости вычислений (которая колеблется довольно амплитудно), стоит добавить time.sleep (0.0001) в каждый кадр, поэтому импортируем еще time.

def main():
    pygame.init()
    DISPLAY = [700,700]
    screen = pygame.display.set_mode(DISPLAY)
    running = True

    earth = Body(m=5.97E+24, x=150E+9, y=0, vx=0, vy=30000, R=5, color='blue')
    sun = Body(m=1.99E+30, x=0, y=0, vx=0, vy=0, R=10, color='yellow')

    params = {
        "G" : 6.6743E-11,
        "T" : 3600,
        "scale" : 6E+8
    }

    solar_system = System([earth, sun], params)
    n = 25
    count = 0
    while running:
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                running = False
        if count % n == 0:
            screen.fill((20, 20, 20))
            for obj in solar_system.objects:
                pygame.draw.circle(screen, obj.color, convert((obj.x, obj.y), params['scale'], DISPLAY), obj.R)
            pygame.display.flip()

        solar_system.iterate()

        count += 1
        time.sleep(0.0001)

    pygame.quit()
    
if __name__ == '__main__':
    main()

Получилась вот такая орбита Земли!

Позднее напишу про то, что можно сделать с этим простейшим симулятором.

Весь код:

import pygame
import math
import time

class Body:
    def __init__(self, m, x, y, vx, vy, R, color='red'):
        self.m = m # масса тела в кг
        self.x = x # начальная координата в м
        self.y = y # начальная координата в м
        self.vx = vx # начальная скорость по x в м/с
        self.vy = vy # начальная скорость по y в м/с
        self.R = R # радиус круга pygame в пикселях
        self.color = color # цвет тела
        self.ax = self.ay = 0 # инициализируем ускорения сил, действующих на тело

    def iterate(self, objects, params):
        self.ax = self.ay = 0 #обнуляем ускорение для пересчета
        G = params['G']
        T = params['T']
        # считаем ускорение от всех сил
        for obj in objects:
            self.ax += G * obj.m * (obj.x - self.x) / math.sqrt((obj.x - self.x)**2 + (obj.y - self.y)**2)**3
            self.ay += G * obj.m * (obj.y - self.y) / math.sqrt((obj.x - self.x)**2 + (obj.y - self.y)**2)**3
        
        self.x += self.vx * T + self.ax * T**2 / 2 # по формуле равноускоренного движения считаем новую координату
        self.y += self.vy * T + self.ay * T**2 / 2

        self.vx += self.ax * T # считаем новую скорость в конце отрезка
        self.vy += self.ay * T

class System:
    def __init__(self, objects, params):
        self.objects = objects
        self.params = params
        self.t = 0 # счетчик прошедшего времени

    def iterate(self):
        for i in range(len(self.objects)):
            obj = self.objects[i]
            obj.iterate(self.objects[:i] + self.objects[i+1:], self.params)
        self.t += self.params['T']

def convert(point, scale, DISPLAY): 
    return (round(point[0] / scale + DISPLAY[0]/2.0), round(-point[1] / scale + DISPLAY[1] / 2.0))

def main():
    pygame.init()
    DISPLAY = [700,700]
    screen = pygame.display.set_mode(DISPLAY)
    running = True

    earth = Body(m=5.97E+24, x=150E+9, y=0, vx=0, vy=30000, R=5, color='blue')
    sun = Body(m=1.99E+30, x=0, y=0, vx=0, vy=0, R=10, color='yellow')

    params = {
        "G" : 6.6743E-11,
        "T" : 3600,
        "scale" : 6E+8
    }

    solar_system = System([earth, sun], params)
    n = 25
    count = 0
    while running:
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                running = False
        if count % n == 0:
            screen.fill((20, 20, 20))
            for obj in solar_system.objects:
                pygame.draw.circle(screen, obj.color, convert((obj.x, obj.y), params['scale'], DISPLAY), obj.R)
            pygame.display.flip()

        solar_system.iterate()

        count += 1
        time.sleep(0.0001)

    pygame.quit()
    
if __name__ == '__main__':
    main()

by Real Universe