Моделирование дипольной антенны в openEMS
В предыдущей части было рассказано как промоделировать распространение ЭМВ при помощи симулятораopenEMS. Теперь рассмотрим как рассчитать что-либо полезное. Промоделируем дипольную полуволновую антенну на частоту 500 МГц. Будет рассмотрено моделирование в частотной области и моделирование диаграммы направленности (ДН) антенны. Схема данной антенны показана на рисунке.
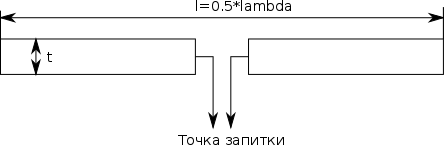
Дипольная антенна состоит из двух лучей, каждый из которых имеет длину равную ¼ волны для резонансной частоты. Запитывается антенна из центра. Антенна имеет сопротивление на чатоте резонанса, равное приблизительно 75 Ом и дигарамму направленности в форме тора. Подробнее о теории работы дипольной антенны можно прочитать, например, в учебнике Айзенберга или Белоцерковского. Эти результаты мы и должны получить после моделирования.
Под катом приведён скрипт с моделью дипольной антенны с построчным разбором. Предполагается, что читатель знаком с основами Matlab/Octave, электротехники и теории антенн (знает что такое комплексное сопротивление, S-параметры и КСВ).
Для тех, кто не в курсе, что здесь происходит, ссылки на мои предыдущие статьи:
Скрипт для моделирования нужно сначала сохранить в текстовый файл с расширением *.m, используя ваш любимый тестовый редактор (например KWrite). Потом нужно запустить Octave с командной строки, передав ему в качестве параметра имя скрипта. Допустим, если наш скрипт называется dipole.m, то симуляция запускается так:
octave dipole.m Если хотим использовать просмотр графиков из Octave в интерактивном режиме, то нужно сначала запустить Octave из командной строки, а затем использовать команду source. Она загрузит скрипт dipole.m из текущего каталога.
source dipole.m В результате моделирования мы хотим получить:
Зависимость входного сопротивления антенны в точки запитки от частоты. Зависимость КСВ антенны в точке запитки от частоты для 50 Ом источника ДН в полярных координатах 3D ДН в сферических координатах Приступим к построчному разбору скрипта. Документация openEMS страдает пробелами, поэтому кое-что пришлось додумывать самому.
Итак в начале скрипта очищаем все переменные:
close all; clear; clc; Теперь нужно объвить имя XML-файла, который содержит задание для моделирования и временный каталог, в котором будут храниться результаты моделирования. Файлы с результатами расчётов достигают 100 Мб, поэтому нужно позаботиться о месте на диске.
physical_constants SimPath = 'tmp'; SimCSX = 'tmp.xml'; Теперь начинаем описание параметрической модели антенны. Это означает, что при изменении параметров (например расчётной резонансной частоты) Matlab/Octave автоматически будет пересчитывать все размеры антенны. Шаг сетки выбираем равным 1/50 длины волны.
f_max = 0.5e9; # расчётная частота резонанса lambda = c0/f_max; # длина волны step=lambda/50; # шаг сетки Как вы помните из физики, длина волны и частота связаны через скорость светаc0
Объявляем пространство моделирования (SimBox) — куб с ребром равнымудвоенной длине волны (2*lambda). Пространство заполняем сеткойmesh.
CSX = InitCSX (); mesh.x = -lambda: step: lambda; mesh.y = -lambda: step: lambda; mesh.z = -lambda: step: lambda; SimBox = [2*lambda 2*lambda 2*lambda]; CSX = DefineRectGrid (CSX,1, mesh); Теперь задаём источник возбуждения. В прошлой части мы использовали синусоидальный источник фиксированной частоты. openEMS сначала проводит расчёт во временной области, а затем пересчитывает результат в частотную область. Поэтому, чтобы смоделировать частотные свойства системы, нужен источник с протяжённым спектром. В качестве такого источника в openEMS доступен Гауссов импульс.
Итак сначала объевляем переменные, в которых будем хранить параметры Гауссова импульса. Нужно задать центральную частоту спектра Гауссова импульса и половину ширины спектра. Мы будем моделировать нашу антенну в полосе частот от 200 МГц до 600 МГц. Следовательно центральная частота будет 400 МГц, а ширина спектра ±200 МГц от центральной частоты.
f0 = 400e6; fc = 0.5*f0; FDTD = InitFDTD ('NrTS',30000); FDTD = SetGaussExcite (FDTD, f0, fc); Пространство FDTD инициализируется при помощи функции InitFDTD () Ей вторым параметром нужно передать количество выборок во временной области. Его нужно подобрать таким образом, чтобы оно превышало длительность импульса в шагах дискретизации. Обычно 30000 бывает достаточно. В противном случае мы получим сообщение об ошибке, которое гласит, что интервал расчёта меньше длительности Гауссова импульса.
Теперь нужно задать граничные условия. Мы моделируем антенну в свободном пространстве, поэтому она со всех сторон будет окружена абсолютно поглощающим диэлектриком MUR
BC = {'MUR','MUR','MUR','MUR','MUR','MUR'}; FDTD = SetBoundaryCond (FDTD, BC); Теперь объявляем геометрию. Процесс описания геометрии для тех кто знаком например с HFSS выглядит необычно и непривычно.
Диполь будет состоять из двух проводящих параллелепипедов, между которыми подключается источник возбуждения. Толщина лучей диполя может быть меньше шага сетки. Как говорит теория, чем больше толщина дипольной антенны, тем шире её полоса пропускания. Вся геометрия у нас параметризована и будет автоматически пересчитываться при изменении параметров. В этом заключается преимущество симулятора, встроенного в Matlab/Octave.
t = step/4; # толщина луча диполя (1/200 длины волны) CSX = AddMetal (CSX,'right_beam'); # правая половинка диполя start = [t -t -t]; # начальная точка stop = [lambda/4 t t]; # конечная точка CSX = AddBox (CSX,'right_beam',1, start, stop); # строим параллелепипед из металла Координаты точек в пространстве задаются в openEMS как матрица-строка из трёх компонентов, которые следуют в порядке [x y z]
Функция AddMetal () добавляет некоторый объект из металла. Созданный объект необходимо ассоциировать с некоторым геометрическим объектом. Функция AddBox () добавляет параллелепипед. Предпоследний и последний параметры — это координаты его крайних вершин. Третий параметр — это приоритет. Его назначение остаётся для меня неясным. Можно установить его всегда равным 1. Второй параметр — имя объекта материала параллелепипеда. Мы должны использовать объект 'right_beam', который мы создали ранее.
Аналогичный действия для левого луча:
CSX = AddMetal (CSX,'left_beam'); start = [0 -t -t]; stop = [-lambda/4 t t]; CSX = AddBox (CSX,'left_beam',1, start, stop); Теперь нужно запитать антенну. Для запитки антенны служит специальный объект, называемый порт (Lumped Port).
Бывает ещё распределённый порт, который представляет собой область пространства из которого распространяется ЭМВ. Распределённый порт использовался во второй части.
Нам нужно использовать обычный порт. Он соответвует случаю запитки антенны от источника напряжения. В качестве источника напряжения выступает объявленный ранее Гауссов импульс. Порт представляет собой две точки в пространстве, между которыми подключаются зажимы виртуального источника напряжения. Сначала объявляем две эти точки. Они должны лежать на поверхности лучей диполя:
start = [0 0 0 ]; # сюда подключаем порт stop = [step 0 0]; Теперь объявим выходное сопротивление источника:
R = 50; И можно добавлять собственно порт:
[CSX port] = AddLumpedPort (CSX,1,1, R, start, stop,[1 0 0], true); Функция AddLumpedPort () имеет 8 параметров. Рассмотрим их подробнее:
Второй параметр — приоритет. Можно поставить в 1 Третий параметр — порядковый номер порта. Может быть несколькопортов. Четвёртый параметр — выходное сопротивление источника Пятый и шестой параметры — точки подключения порта Седьмой параметр — направление сигнала. Вектор из трёх компонентов, который показывает направление сигнала в формате [x y z]. У нассигнал направлен вдоль оси X. Теперь нужно задать область в которой будет рассчитываться поле, излучаемое антенной. openEMS расчитывает поле в ближней зоне, а затем при помощи постпроцессора NF2FF пересчитывает его в поле в дальней зоне. ДН антенны рассчитывается по полю в дальней зоне. Область в которой, рассчитывается поле, нужно принять равной области моделирования, обязательно отступив внутрь несколько шагов сетки от границы.
SimBox = SimBox-step*4.0; # отступаем от границы [CSX nf2ff] = CreateNF2FFBox (CSX,'nf2ff',-SimBox/2, SimBox/2); Всё! Геометрия задана. Можно записать файл задания для openEMS и посмотреть результат в интерактивном просмотровщике AppCSXCAD.
mkdir ('tmp');
SimPath = 'tmp/tmp.xml'
WriteOpenEMS (SimPath, FDTD, CSX);
CSXGeomPlot (SimPath);
Если всё сделали правильно, то увидим следующую картинку (в зазоре диполя виден порт):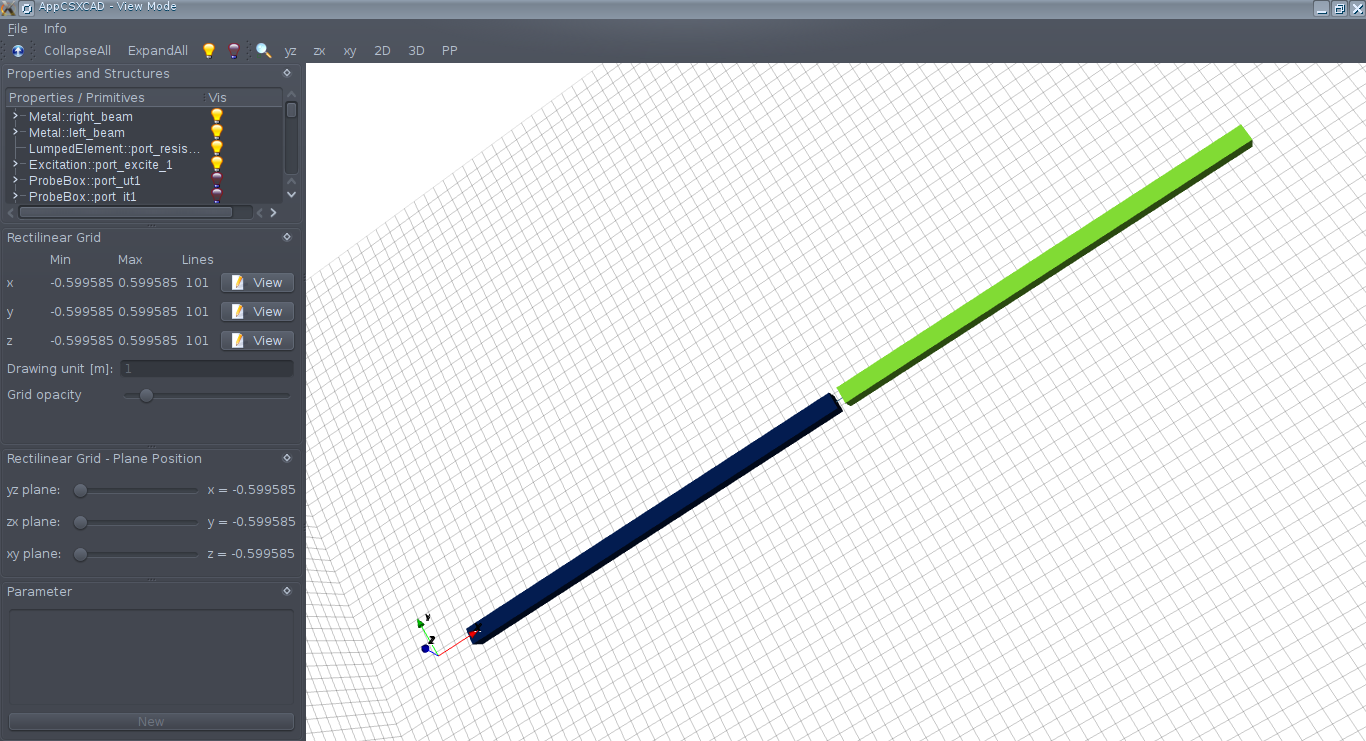 
Тепрь запускаем openEMS.
RunOpenEMS ('tmp','tmp.xml'); Расчёт идёт довольно долго. После расчёта создаются для структуры:
port — содержит информацию о характеристиках антенны вчастотной области nf2ff — содержит информацию о ДН антенны Нам нужно извлечь из структуры port информацию о входном сопротивлении антенны и коэффициенте отражения S11. Для этого понадобятся следующие поля структурыport:
port.uf.tot — Полное напряжение на зажимах порта port.if.tot — Полный ток, протекающий через порт port.uf.inc — Амплитуда напряжения падающей волны port.uf.ref — Амплитуда напряжения отражённой волны Тепрь при помощи формул, известных из курса радиотехники, рассчитываем входной сопротивление Zin и коэффициент отражения по входу S11 (его можно пересчитать вкоэффициент стоячей волны — КСВ). Теперь можно построть графики Zвх (активной и реактивной части), КСВ и S11, используя стандартные средства Matlab/Octave Этот кусок кода не требует пояснений.
freq = linspace (f0-fc, f0+fc,501); # ось частот port = calcPort (port,'tmp', freq); # извлекаем параметры Zin = port.uf.tot ./ port.if.tot; S11 = port.uf.ref ./ port.uf.inc;
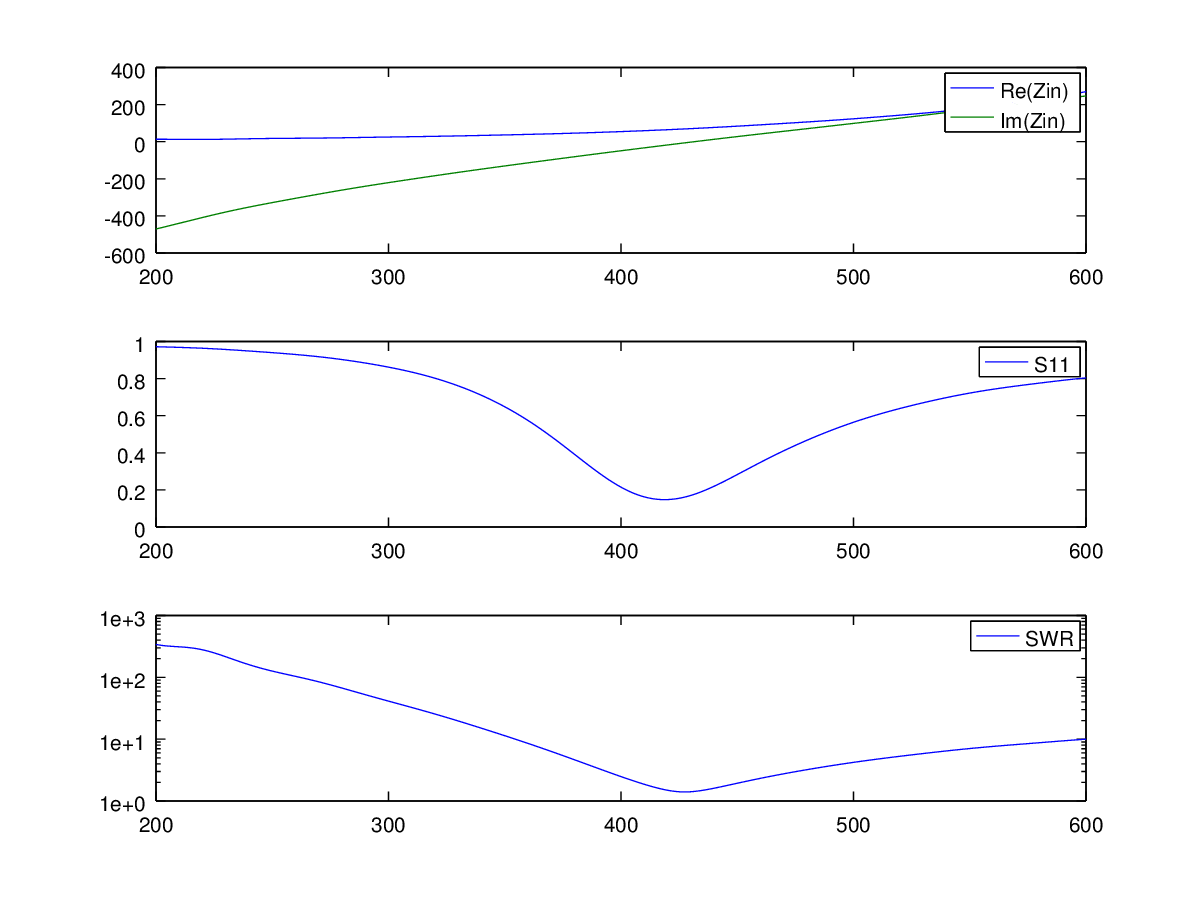
subplot (3,1,1); plot (freq/1e6, real (Zin), freq/1e6, imag (Zin)); # строим графики Rвх и Xвх legend ('Re (Zin)','Im (Zin)'); subplot (3,1,2); plot (freq/1e6, S11); # строим график S11 swr = (1+abs (S11))./(1-abs (S11)); # найдём точку минимального КСВ [swr_min idx] = min (swr); [Xmin idx1] = min (abs (imag (Zin))); # и точку резонанса fr = freq (idx); fr1 = freq (idx1); Zr = Zin (idx); Zr1 = Zin (idx1); disp («Minimum SWR frequency:»); # выведем параметры антенны disp (fr); disp («Resonant frequency (jX=0)»); disp (fr1); disp («Impedance at minimum SWR»); disp (Zr); disp («Impedance at resonant frequency»); disp (Zr1); disp («Minimum SWR:»); disp (swr_min); subplot (3,1,3); semilogy (freq/1e6, swr); Получаем следующие параметры антенны. Видно, что частота резонанса ушла вниз от расчётной. Сопротивление антенны в резонансе 71,2 Ом — почти как в учебниках, отклонение вызвано толщиной диполя.
Minimum SWR frequency:
427200000
Resonant frequency (jX=0)
431200000
Impedance at minimum SWR
68.7692 — 6.5511i
Impedance at resonant frequency
71.18555 — 0.45064i
Minimum SWR:
1.4013
Теперь рассчитаем ДН в полярных координатах. Последние два параметра функции CalcNF2FF () — это диапазон углов в пределах которых рассматривается ДН. Третьим параметром ей нужно передать частоту, на которой рассчитывается ДН.Получаем следующие графики:
nf2ff = CalcNF2FF (nf2ff,'tmp', fr,[-180:2:180]*pi/180,[0 90]*pi/180);
figure
polarFF (nf2ff,'xaxis','theta','param',[1 2],'normalize',1);
ДН в декартовых координатах:
figure
plotFFdB (nf2ff,'xaxis','theta','param',[1 2]);
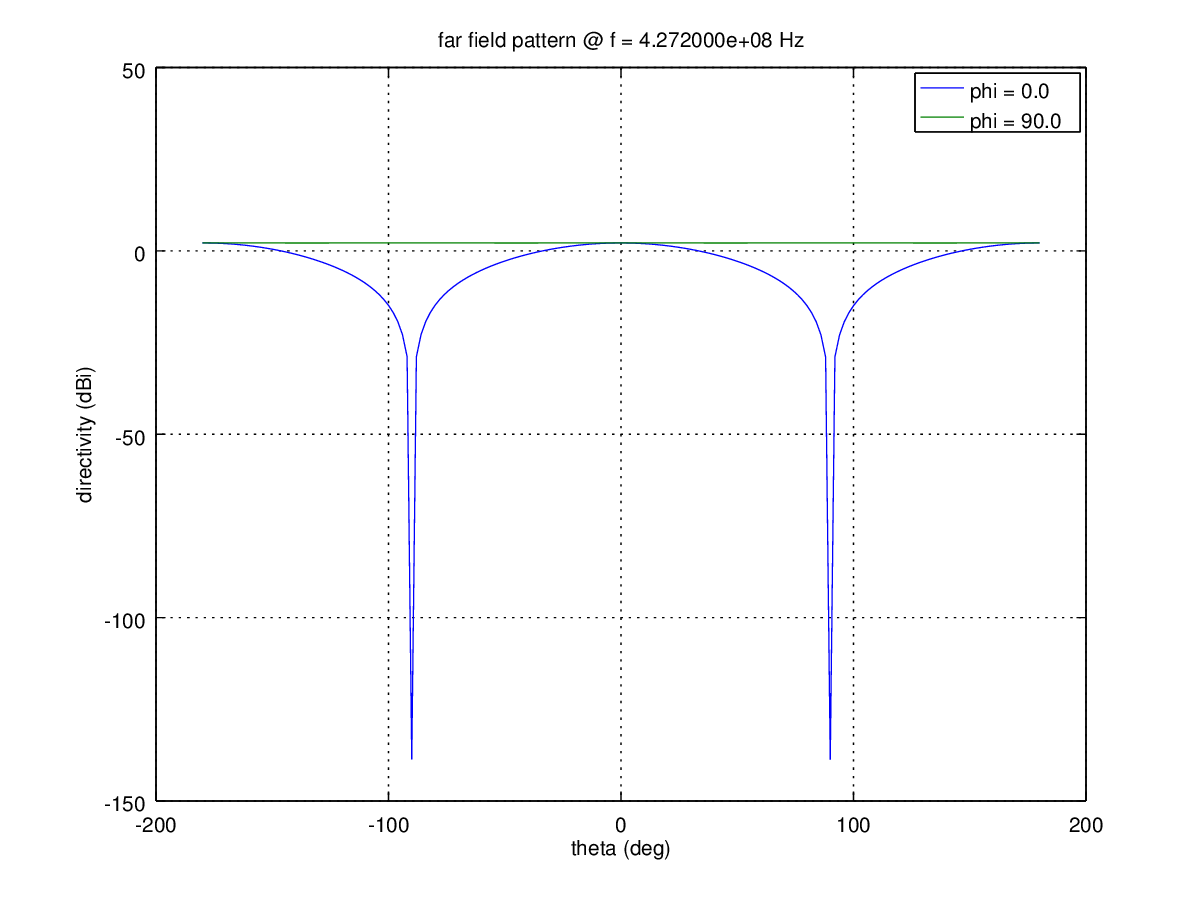
thetaRange = (0:2:180);
phiRange=(0:2:360)-180;
nf2ff =
CalcNF2FF (nf2ff,'tmp', fr, thetaRange*pi/180, phiRange*pi/180,'Verbose',1,'Outfile'
,'3D_Pattern.h5');
figure
plotFF3D (nf2ff,'logscale',-20);
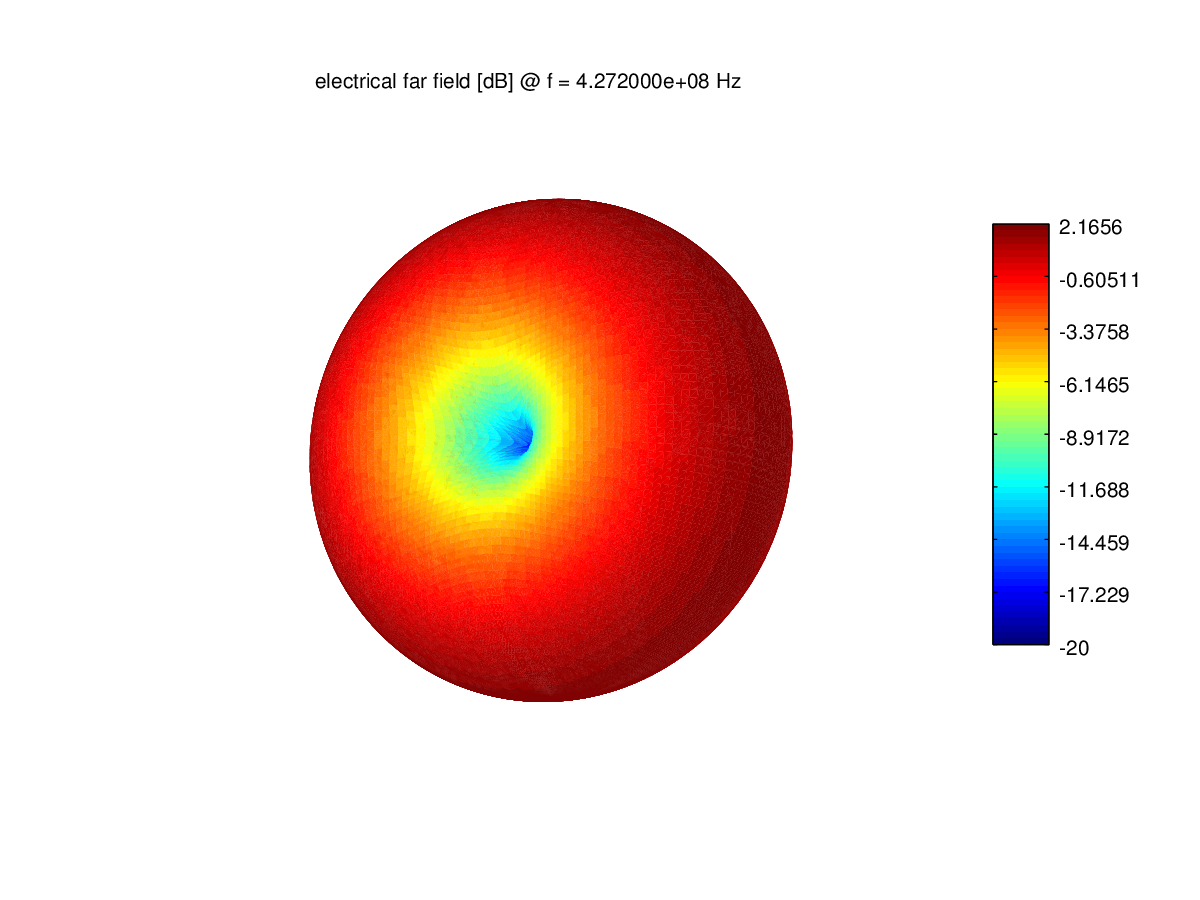
Пространственная ДН имеет форму тора как в учебниках по антеннам. Коэффициентусиления антенны 2,1 дБ.
Ещё можно создать файл *.vtk, чтобы его потом просматривать при помощи Paraview:
E_far_normalized = nf2ff.E_norm{1} / max (nf2ff.E_norm{1}(:)) * nf2ff.Dmax; DumpFF2VTK (['tmp/3D_Pattern.vtk'], E_far_normalized, thetaRange, phiRange,'scale', 1e-3); Вот так ДН выглядит в Paraview (нужно открывать файл 3D_Pattern.vtk):
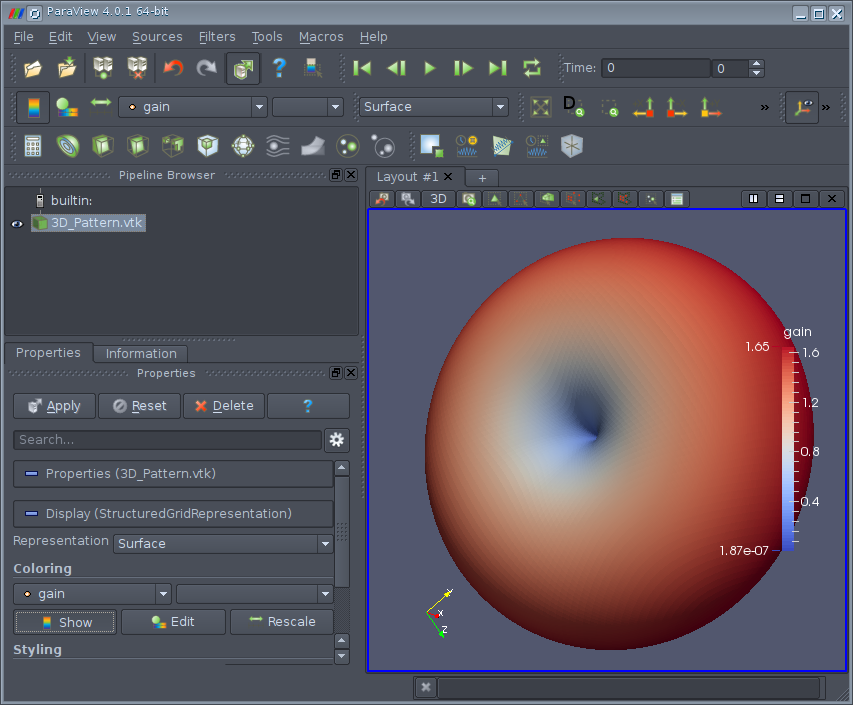
Мы промоделировали дипольную антенну в диапазоне частот от 200 до 600 МГц. Как видно, моделирование даёт результаты близкие к теории и позволяет учитывать влияние отклонения параметров диполя от идеальных. Те, у кого есть под рукой HFSS могут проверить результат.
В заключении приведём наш скрипт целиком
Скрытый текст close all; clear; clc;
physical_constants #unit = 1e-3; # Units in mm SimPath = 'tmp'; SimCSX = 'tmp.xml';
f_max = 0.5e9; lambda = c0/f_max;
dipole_L = lambda/2; step=lambda/50;
CSX = InitCSX ();
mesh.x = -lambda: step: lambda; mesh.y = -lambda: step: lambda; mesh.z = -lambda: step: lambda; SimBox = [2*lambda 2*lambda 2*lambda];
CSX = DefineRectGrid (CSX,1, mesh);
#f0 = f_max; f0 = 400e6; fc = 0.5*f0; FDTD = InitFDTD ('NrTS',30000); FDTD = SetGaussExcite (FDTD, f0, fc); BC = {'MUR','MUR','MUR','MUR','MUR','MUR'}; FDTD = SetBoundaryCond (FDTD, BC);
t = step/4; CSX = AddMetal (CSX,'right_beam'); start = [t -t -t]; stop = [lambda/4 t t]; CSX = AddBox (CSX,'right_beam',1, start, stop);
CSX = AddMetal (CSX,'left_beam'); start = [0 -t -t]; stop = [-lambda/4 t t]; CSX = AddBox (CSX,'left_beam',1, start, stop);
start = [0 0 0 ]; stop = [step 0 0]; R = 50; [CSX port] = AddLumpedPort (CSX,1,1, R, start, stop,[1 0 0], true); SimBox = SimBox-step*4.0; [CSX nf2ff] = CreateNF2FFBox (CSX,'nf2ff',-SimBox/2, SimBox/2);
mkdir ('tmp'); SimPath = 'tmp/tmp.xml' WriteOpenEMS (SimPath, FDTD, CSX); CSXGeomPlot (SimPath);
RunOpenEMS ('tmp','tmp.xml');
freq = linspace (f0-fc, f0+fc,501); port = calcPort (port,'tmp', freq); Zin = port.uf.tot ./ port.if.tot; S11 = port.uf.ref ./ port.uf.inc;
subplot (3,1,1); plot (freq/1e6, real (Zin), freq/1e6, imag (Zin)); legend ('Re (Zin)','Im (Zin)'); subplot (3,1,2); plot (freq/1e6, S11); legend ('S11'); swr = (1+abs (S11))./(1-abs (S11)); [swr_min idx] = min (swr); [Xmin idx1] = min (abs (imag (Zin))); fr = freq (idx); fr1 = freq (idx1); Zr = Zin (idx); Zr1 = Zin (idx1); disp («Minimum SWR frequency:»); disp (fr); disp («Resonant frequency (jX=0)»); disp (fr1); disp («Impedance at minimum SWR»); disp (Zr); disp («Impedance at resonant frequency»); disp (Zr1); disp («Minimum SWR:»); disp (swr_min); subplot (3,1,3); semilogy (freq/1e6, swr); legend ('SWR');
nf2ff = CalcNF2FF (nf2ff,'tmp', fr,[-180:2:180]*pi/180,[0 90]*pi/180); figure polarFF (nf2ff,'xaxis','theta','param',[1 2],'normalize',1);
figure plotFFdB (nf2ff,'xaxis','theta','param',[1 2]);
thetaRange = (0:2:180); phiRange=(0:2:360)-180; nf2ff = CalcNF2FF (nf2ff,'tmp', fr, thetaRange*pi/180, phiRange*pi/180,'Verbose',1,'Outfile' ,'3D_Pattern.h5'); figure plotFF3D (nf2ff,'logscale',-20);
E_far_normalized = nf2ff.E_norm{1} / max (nf2ff.E_norm{1}(:)) * nf2ff.Dmax; DumpFF2VTK (['tmp/3D_Pattern.vtk'], E_far_normalized, thetaRange, phiRange,'scale', 1e-3);
pause; Возможно, продолжение следует…
