Модель камеры08.01.2023 17:16

Модель камеры описывает преобразование из 3D координат сцены в 2D координаты изображения.

В статье будет подробно рассказано о модели, описывающей бо́льшую часть современных камер. Будут затронуты такие понятия как камера обскура, пинхол камера, фокусное расстояние, глубина резкости, дисторсия и т.д. Статья будет особенно полезна, если вы занимаетесь или планируете заниматься фотографией, компьютерным зрением или компьютерной графикой.

Камера обскура

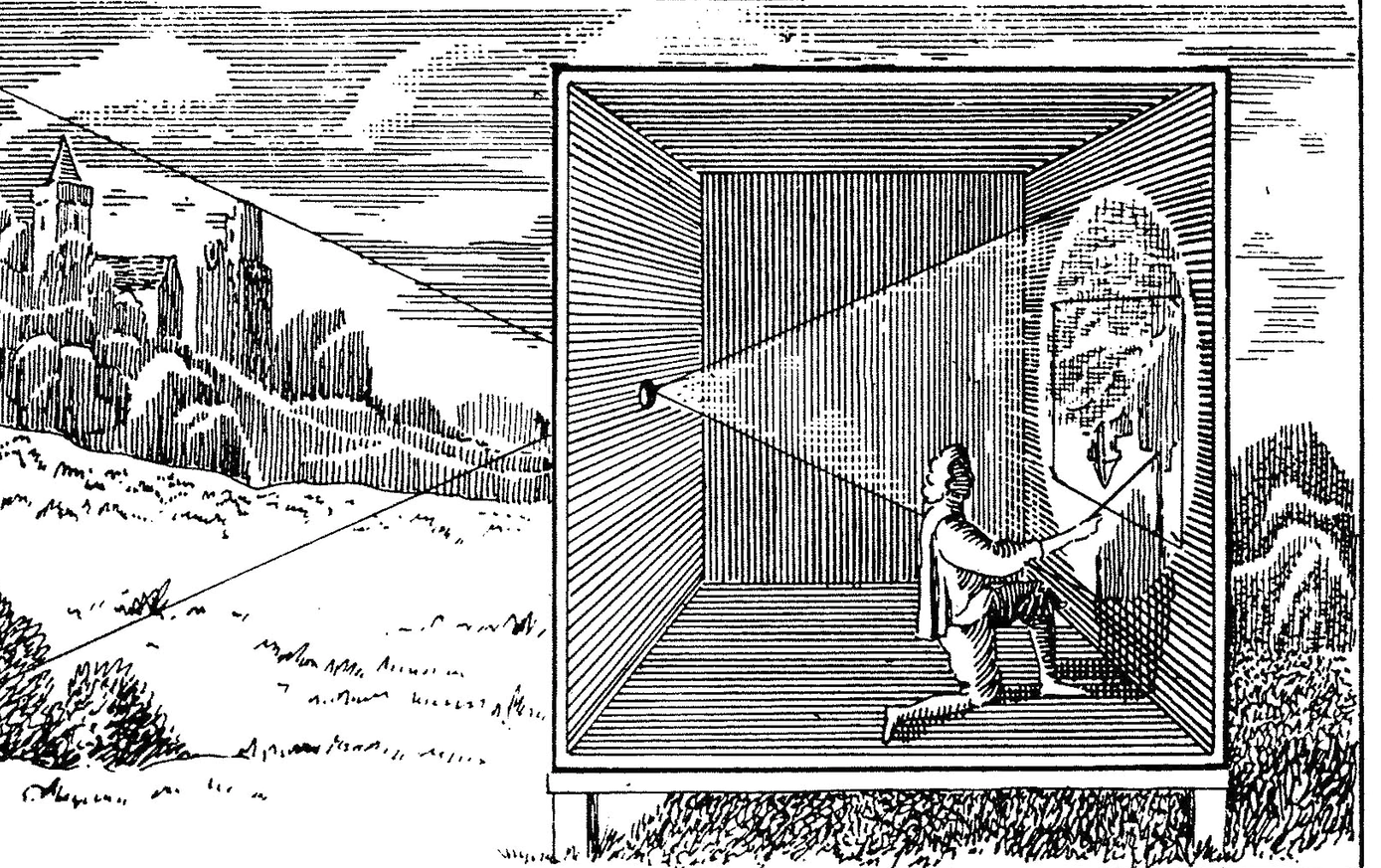камера-обскура

Камера-обскура (лат. camera obscūra — «тёмная комната») — один из предшественников современных камер. Представляет собой тёмную комнату. На одной из стен располагается холст. На противоположной стене небольшое отверстие. Лучи света, проходя через отверстие, формируют на стене перевёрнутое изображение мира.

Такие помещения использовались художниками для рисования пейзажей.

проекция улицы с помощью камеры-обскура проекция улицы с помощью камеры-обскура

На картинке слева можно увидеть пример изображения, формирующегося на стене. Эта фотография была снята с большой выдержкой. В реальности же картинка на стене будет весьма тусклой.

Современные камеры похожи на камеру-обскура не только названием. Формирование изображения в современных камерах происходит похожим образом и моделируется одной и той же моделью, что и в «тёмной комнате».

Пинхол камера

пинхол камера

Пинхол камера (англ. pinhole от pin «булавка» + hole «отверстие») — камера, работающая по принципу камеры-обскура.

По сути это уменьшенная версия «тёмной комнаты», где вместо холста напротив отверстия находится фотоматрица (фотоплёнка, сенсор).

Ещё на пинхол камеру можно смотреть как на камеру (в современном понимании), у которой объектив заменили на заглушку с небольшим отверстием.

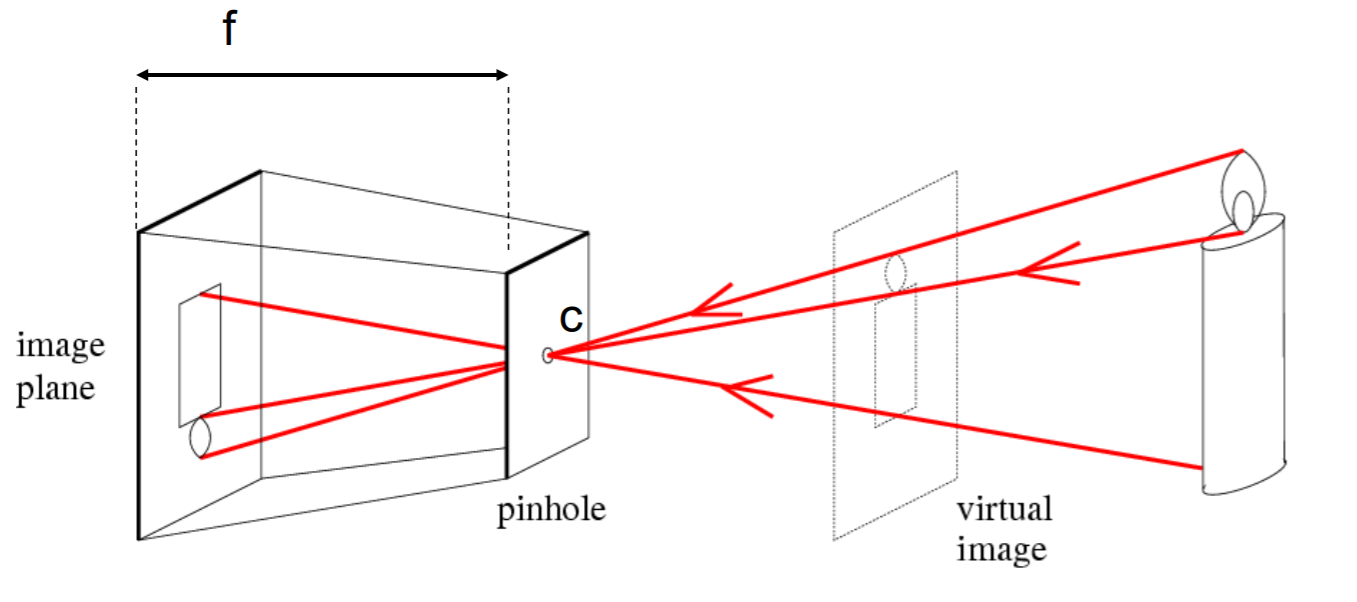формирование изображения в пинхол камере формирование изображения в пинхол камере

Посмотрите на картинку слева. На ней показано как формируется изображение в пинхол камере.

Справа находится свеча — трёхмерный объект, проекцию которого мы хотим получить. Буквойобозначено отверстие нашей камеры. Слева находится плоскость изображения, в которой находится наш сенсор. В этой плоскости, проходящими через отверстие лучами, формируется перевёрнутое изображение свечи. Буквойобозначено фокусное расстояние — расстояние от сенсора (плоскости изображения) до отверстия.

Часто для удобства работы и размышлений вместо плоскости изображения рассматривают виртуальную плоскость изображения. Она находится на расстоянии f перед отверстием и на ней «виртуально» формируется такое же изображение, как и на сенсоре, но уже не перевёрнутое.

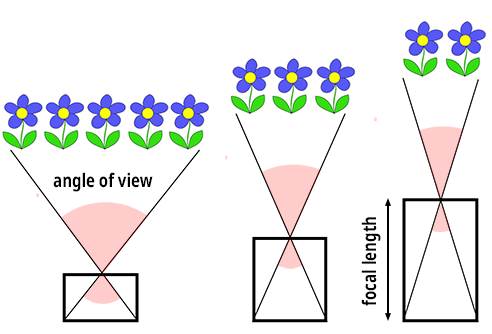влияние фокусного расстояния

Если считать что размер сенсора (плоскости изображения/фотоматрицы/фотоплёнки) фиксирован, то единственным параметром пинхол камеры является её фокусное расстояние.

Фокусное расстояние влияет на угол обзора камеры и на то под каким углом падают лучи на плоскость изображения. Чем больше фокусное расстояние, тем меньше угол обзора.

фотографии девушки с разным фокусным расстоянием фотографии девушки с разным фокусным расстоянием

Изменение фокусного расстояния может сильно влиять на то, как объект будет выглядеть в проекции.

На картинке слева находятся несколько фотографий, снятых с разными фокусными расстояниями таким образом, чтобы объект съёмки полностью занимал кадр. Фотографии с маленьким фокусным расстояниям сняты с близкой дистанции и наоборот.

Обратите внимание, как сильно меняются черты лица при изменении углов лучей, которыми формируется изображение.

У пинхол камеры есть множество недостатков по сравнению с обычной камерой:

в реальности отверстие имеет ненулевой размер. А значит в каждую точку сенсора попадает ни один луч, а множество лучей. Что делает изображение размытым. И чем больше отверстие, тем более размытое получится изображение;
сделать отверстие пренебрежимо малым также нельзя. Когда отверстие очень мало в дело вступает такое физическое явление как дифракция. Для заданной длины волны и заданного фокусного расстояния существует оптимальный размер отверстия. Подробнее можно почитать тут;
каждая точка на изображении формируется небольшим количеством света. Для получения хорошего изображения нужен чувствительный сенсор и большая (иногда очень большая) выдержка.

Но пинхол камеры используют и сейчас так как у них есть и преимущества:

большая (по сути бесконечная) глубина резкости (об этом ниже);
простота, дешивизна и возможность миниатюризации;
«правильное» изображение (отсутствие дисторсии. Об этом ниже);
возможность использовать там, где оптические системы использовать нельзя. Например, если вместо фотоплёнки расположить массив детекторов частиц, то можно получить «фотографии» количества частиц, прилетевших с определённых направлений. Это уже не совсем камера, но принцип очень похож.

Оптическая система из одной линзы

Модель пинхол камеры (без учёта дисторсии) моделирует бо́льшую часть используемых камер (например, камеры мобильных телефонов, зеркальные фотоаппараты и т.д.).

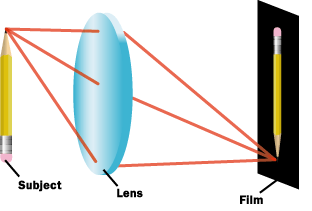модель камеры

Обычную камеру можно смоделировать пинхол камерой с линзой, вместо отверстия.

При этом термины используются те-же: плоскость изображения — плоскость, где находится сенсор, фокусное расстояние — расстояние от центра линзы до плоскости изображения.

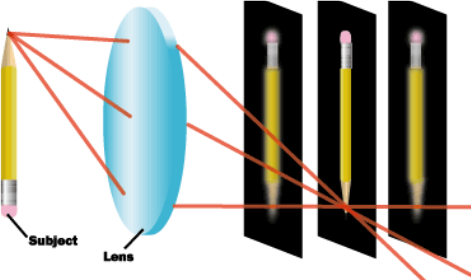
Обратите внимание на картинку слева. Лучи, проходящие через центр линзы, ведут себя в точности также как лучи, проходящие через отверстие в пинхол камере. При этом остальные лучи сходятся в той же точке, куда падает центральный луч. Это решает все основные проблемы пинхол камеры — на сенсор падает много света, который собирается со всей площади линзы, и изображение не размывается (при условии, что все лучи сходятся в одной точке).

фокус

Но лучи от объекта съемки могут и не сойтись в плоскости изображения.

Для фиксированного фокусного расстояния (положения сенсора) есть оптимальная глубина на которой должен располагаться объект, чтобы все лучи от этого объекта сходились в плоскости изображения. Тогда говорят что объект находится в фокусе. И наоборот, для фиксированного положения объекта есть оптимальное фокусное расстояние (среднее положение сенсора на картинке слева).

глубина резкости

Диапазон глубины (расстояния от камеры) при котором лучи от объекта съемки сходятся примерно на сенсоре (например, с ошибкой меньше размера пикселя) называется глубиной резкости.

Обратите внимание, что в пинхол камере такого понятия в принципе нет, потому что лучи не фокусируются.

В большинстве алгоритмов компьютерного зрения считают что объект съемки находится в фокусе. Таким образом задачу держать объект в фокусе перекладывают на плечи фотографов и видеооператоров.

диафрагмой можно контролировать глубину резкости

Посмотрите на картинку выше (с тремя плоскостями изображения). При расположении сенсора в самой левой плоскости изображения картинка будет сильно размытой. Теперь представьте что вы закрыли всю поверхность линзы, кроме небольшого отверстия в центре. Теперь из всех лучей через линзу проходит только центральный луч. Света будет мало, но при этом изображение на сенсоре будет не размытым. По сути мы получили пинхол камеру.

Если закрывать не всю линзу, а часть, то мы получим что-то посередине. Мы убираем часть лучей с края линзы и получаем меньше света, но при этом увеличивается глубина резкости (уменьшается пятно размытия). Фотографы пользуются диафрагмой, чтобы закрывать часть линзы и контролировать глубину резкости, количество света на сенсоре и некоторые другие параметры.

Сложные оптические системы

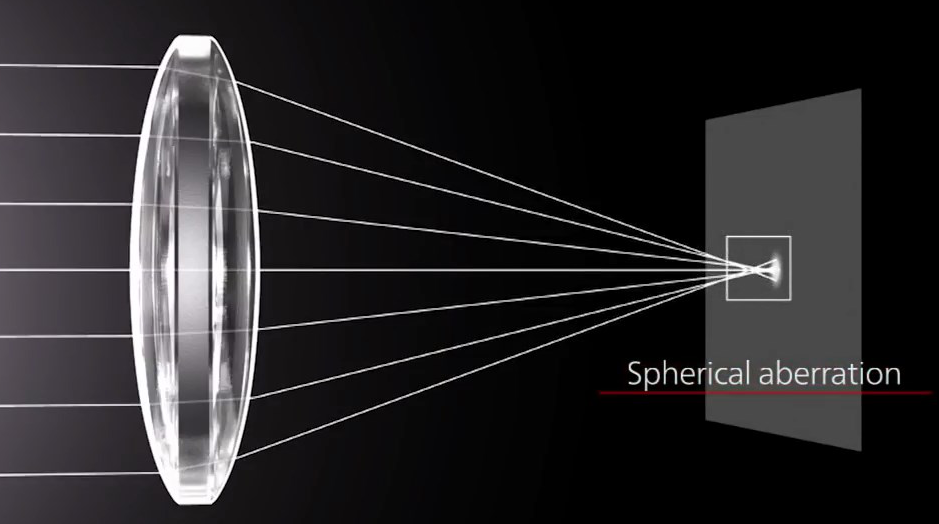сферическая аберрация

Как модель можно представлять оптическую систему камеры как одну линзу. Но в реальности с одной линзой будут возникать разные оптические искажения. Например, сферическая аберрация и хроматическая аберрация.

Для исправления искажений в оптическую систему добавляют дополнительные линзы. Например, как в простейшем анастигмате — объективе триплет.

зеркальная камера Canon в разрезе, видна система линз, некоторые из линз подвижны зеркальная камера Canon в разрезе, видна система линз, некоторые из линз подвижны

Кроме исправления искажений линзы в оптическую систему камеры добавляют для фокусировки, изменения фокусного расстояния и стабилизации. Современные объективы содержат сложную систему линз разной формы и из разных материалов.

Системой линз исправляют большую часть оптических искажений. Часто остающееся искажение — дисторсия.

Дисторсия

Дисторсия — один из видов искажений в оптических системах, часто встречающийся в современных камерах. В результате линии, которые в реальности прямые, на изображении выглядят изогнутыми. В большинстве современных камер дисторсия небольшая. А с использованием ортоскопических объективов можно добиться околонулевой дисторсии.

Дисторсия вносит искажения (по сравнению с пинхол камерой) в пространстве изображения. Это когда лучи попадают не в тот пиксель в который должны, а рядом. Для исправления изображения с дисторсией достаточно сместить каждый пиксель на его «законное» место. Дисторсия не зависит от того что вы снимаете. Но зависит он конфигурации оптической системы камеры. В том числе от зума.

Существует множество моделей дисторсии. Большинство искажений в камерах можно исправить используя модель радиальной дисторсии.

исправления

Для камеры с фиксированной конфигурацией линз можно снять изображение с множеством прямых линий (например, шахматную доску, как на картинке слева), найти линии которые должны быть прямыми и подобрать параметры выбранной модели дисторсии чтобы эти линии выпрямились. После, эти параметры можно использовать для исправления всех изображений, полученных с помощью этой камеры.

Модель пинхол камеры

Не считая дисторсию, которую можно исправить или игнорировать, для моделирования современных камер можно использовать модель пинхол камеры.

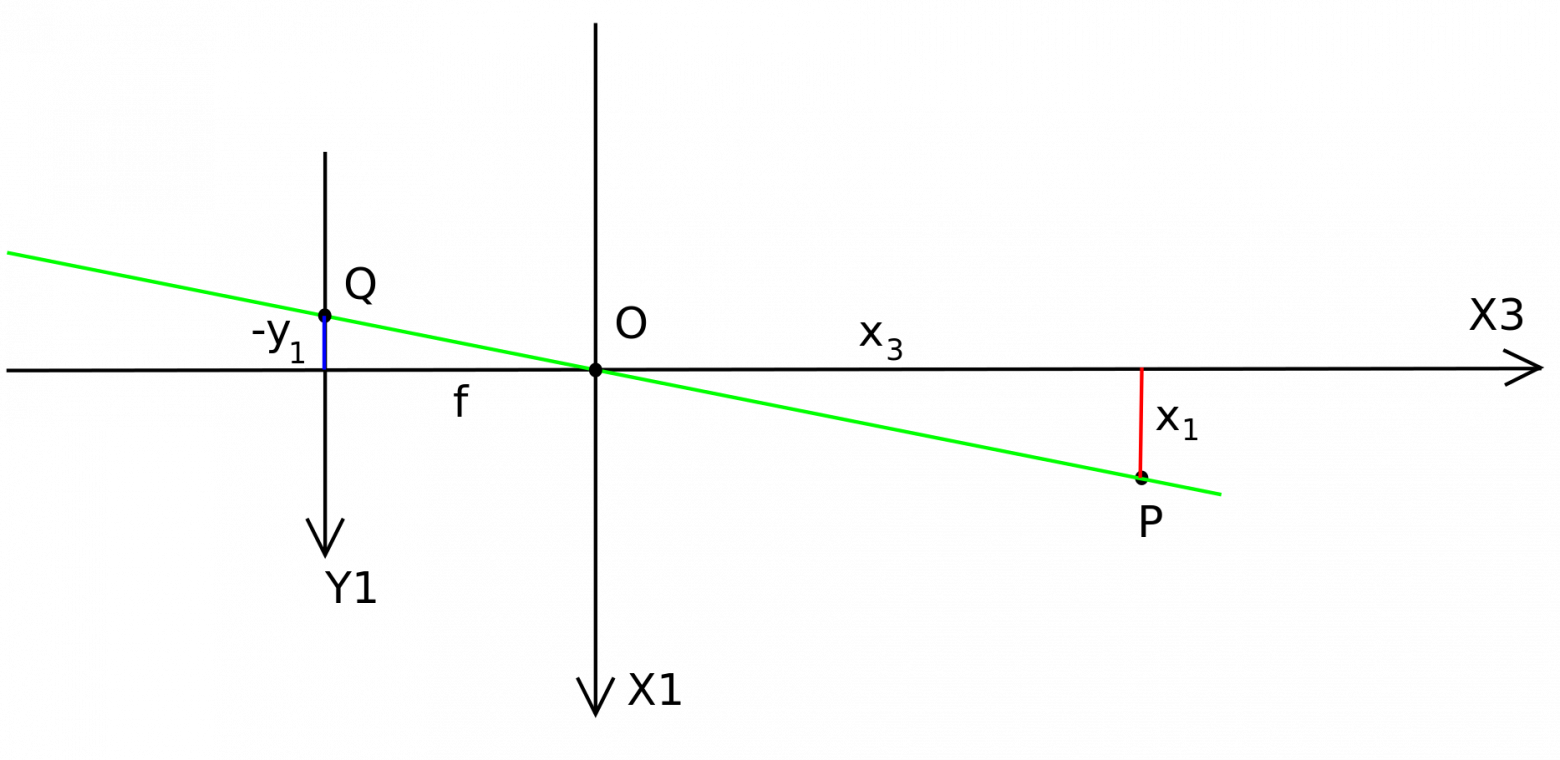модель пинхол камеры (в общем виде) модель пинхол камеры (в общем виде)

Давайте выведем формулы преобразования 3D координат сцены в 2D координаты в плоскости изображения для пинхол камеры.

Будем считать что отверстие пинхол камеры находится в точке [0, 0, 0] нашего 3D пространства, ось X_3 направлена вперёд, относительно камеры, ось X_1 — вправо, а ось X_2 — вниз.

На картинке можно видеть изображение пространства сверху (вдоль оси X_2 ). Осью Y_1 обозначена ось плоскости изображения, направленная вправо. Фокусное расстояние обозначено буквой .

Пусть P = [x_1, x_2, x_3] точка нашего пространства. Давайте выведем координаты точки Q = [y_1, y_2] , находящейся на плоскости изображения.
Обратим внимание, что треугольники со сторонами (-y_1, QO, f) и (x_1, PO, x_3) подобны.
Отсюда можно выразить. y_1 . Опустим выражение y_2 , логика там такая же.

Получим $y_1 = -\frac{fx_1}{x_3}$ .

Обратите внимание, масштаб что одного, что второго треугольника не важны. Мы можем увеличить всё 3D пространство в 10 раз и получим то-же изображение. Нам не важно заданы x_1, x_3 в метрах или дюймах. Важно только их отношение.

Так же мы можем свободно менять единицы в которых у нас заданы y_1, f . Но они должны быть в одних единицах измерения! Если у нас фокусное расстояние задано в миллиметрах, то по этой формуле мы получим координаты в плоскости изображения в миллиметрах. Часто полезно работать в координатах пикселей. Соответственно размер фокусного расстояния переводить из миллиметров в пиксели. Это полностью легально т.к. в фотоматрице пиксели имеют физический размер.

Разные модели пинхол камеры могут немного различаться. Например, направлением осей в 3D и 2D пространствах.

Самое главное — для получения координаты в плоскости изображения нужно умножить одну из координат 3D точки на фокусное расстояние и поделить на глубину 3D точки.

Модель камеры OpenCV

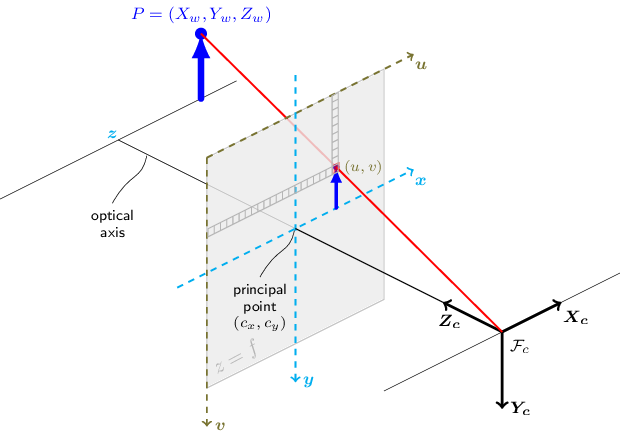модель камеры OpenCV

Модель пинхол камеры из библиотеки OpenCV — одна из популярных и часто использующихся моделей пинхол камеры.

Ось 3D пространства направлена вперёд, ось — вправо, — вниз.

Здесь используется виртуальная плоскость изображения. Осьнаправлена вправо, ось — вниз. Координаты заданы в пикселях. Центр изображения (точка вдоль оси ) находится в пикселе (c_x, c_y) . А пиксель (0, 0) находится в левом верхнем углу изображения.

Модель камеры OpenCV параметризуется 4 числами, заданными в пикселях: (f_x, f_y, c_x, c_y) . Формулы для преобразования координат 3D точки (x, y, z) в точку (u, v) на изображении выглядят следующим образом:

$u= \frac{f_xx}{z} + c_x, v = \frac{f_yy}{z} + c_y$

Параметры (c_x, c_y) задают центр изображения в пикселях. В большинстве ситуаций центр изображения будет в точке (w/2, h/2) , где и это ширина и высота изображения в пикселях. Центр изображения может быть смещён. Например, если изображение, с которым мы работаем, это не оригинальный кадр сделанный камерой, а обрезанный кадр. Важно чтобы (c_x, c_y) соответствовали оптической оси камеры.

Параметры (f_x, f_y) задают фокусное расстояние, выраженное в «ширинах» в «высотах» пикселя. В большинстве случаев пиксели в изображении квадратные. Тогда эти параметры равны и соответствуют физическому понятию фокусного расстояния f = f_x = f_y . Иногда приходится работать с изображениями, где пиксели неквадратные. Например, при съемке анаморфными объективами. Тогда растяжение вдоль одной из осей выражается в модели как разные фокусные расстояния.

Модель камеры OpenGL

Коротко про вторую популярную модель пинхол камеры.

Понятия камеры (или модели камеры) в OpenGL нет. Но чаще всего операция проекции в компьютерной графике задаётся следующей матрицей гомографии 4×4:

$P = \begin{bmatrix} f_x & 0 & 0 & 0 \\ 0 & f_y & 0 & 0 \\ 0 & 0 & \frac{far+near}{near-far} & \frac{2far \times near}{near-far} \\ 0 & 0 & -1 & 0 \end{bmatrix}$

При этом считают что оси в 3D пространстве направлены так: — назад, — вправо, — вверх. А в 2D пространстве оси направлены вправо и вверх, с центром в точке (0, 0) . А фокусные расстояния задаются в размерах дисплея (так, чтобы плоскость изображения находилась в квадрате $[-1, 1] \times [-1, 1]$ ).

Не будем сейчас разбирать что такое гомография, однородные координаты, far, near. А просто выпишем как из 3D точки (x, y, z) получается точка (u, v) :

$u = -\frac{f_xx}{z}, v = -\frac{f_yy}{z}$ . Формулы немного различаются, но суть та-же.

Например, тут стоит минус, потому что ось направлена назад и глубина точки это .

Практическое применение

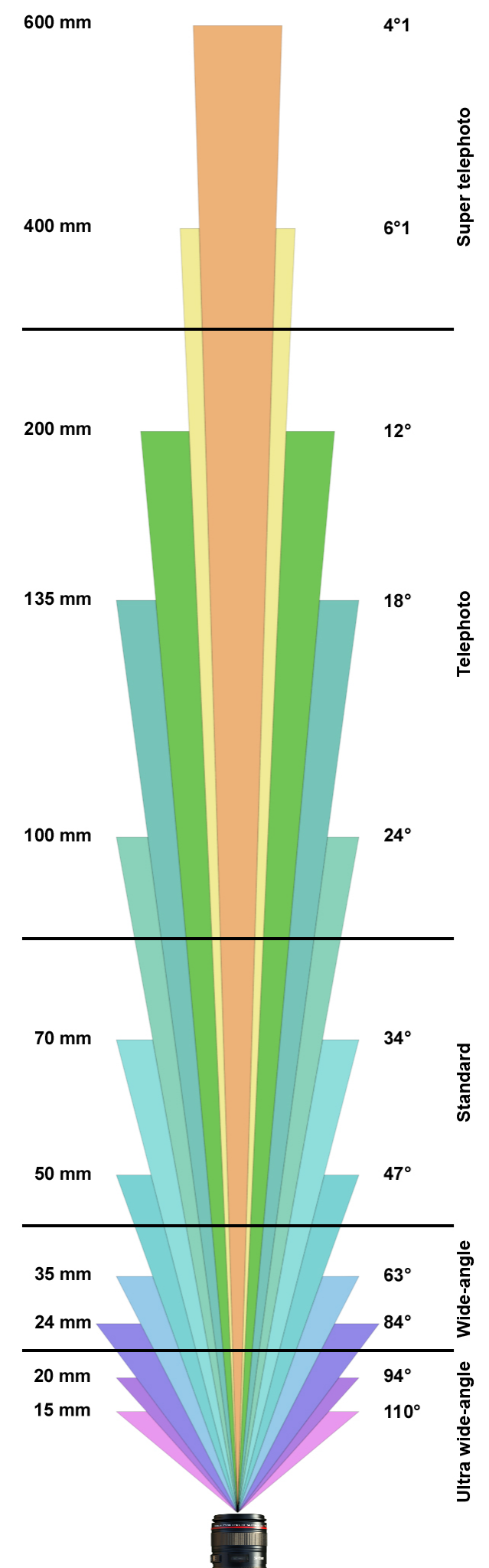фокусное расстояние в сравнении с диагональным углом обзора (для full frame камеры) фокусное расстояние в сравнении с диагональным углом обзора (для full frame камеры)

Давайте возьмём какую-нибудь Full Frame камеру и посчитаем для неё параметры модели пинхол камеры OpenCV.

Например, камеру Canon EOS 5D Mark II. Размер её фотоматрицы $36mm\times24mm$ в миллиметрах или $5616px\times3744px$ в пикселях. Обратите внимание, что соотношение сторон в пикселях и миллиметрах равны. Значит пиксели квадратные и для перевода из миллиметров в пиксели можем просто домножать миллиметры на 5616/36 = 3744/24 = 156 .

К камере подберём подходящий объектив. Например, Canon EF 50mm f/1.8 STM. Это объектив с фиксированным фокусным расстоянием f=50mm (при использовании с full frame камерой). Давайте пересчитаем фокусное расстояние в пиксели: $f_{px}=50\times156 = 7800px$ .

Соберём всё вместе и получим следующие параметры модели камеры OpenCV:

f_x = f_y = 7800,
c_x = 5616/2 = 2808,
c_y = 3744/2 = 1872

На картинке слева для Full frame камер представлены значения фокусного расстояния и соответствующие им значения диагонального угла обзора. Угол обзора можно посчитать как двойной угол $\measuredangle (QO, f)$ по следующей формуле:

$\alpha = 2\arctan{\frac{d}{2f}}$ ,

где — диагональ матрицы.

В случае Full frame камеры ( $d = \sqrt{36^2 + 24^2} \approx 43.26$ ) и f=50mm получим:

$\alpha = 2\arctan{\frac{43.26}{100}}\approx46.8^{\circ}$ .

Иногда считают также горизонтальный или вертикальный углы обзора (вместо используется или ).

Так же на картинке можно видеть термины, которыми обозначают тип объективов (камер). Например, телефото объективом считается объектив с большим фокусным расстоянием (малым углом обзора), а сверхширокоугольными называют камеры с большим углом обзора (маленьким фокусным расстоянием).

Заключение

Целью статьи было подробно рассказать о модели пинхол камеры, и о том почему она подходит для моделирования современных фото и видеокамер.

Мы подробно разобрали как в камерах формируется изображение и вывели соответствующие формулы.

Описанные в статье термины и формулы будут полезны всем, кто занимается или планирует заниматься компьютерным зрением (например, задачами отслеживания камеры или 3D реконструкции, дополненной реальностью и т.д.), компьютерной графикой (для понимания связи между реальными и виртуальными камерами) или фотографией (для понимания принципов работы камеры и соответствующей математики).