Минисериал: троичный компьютер своими руками
Многие утверждали, что строят троичный компьютер, однако, насколько мне известно, никто не завершил проект. Проект Триадор не дает пустых обещаний!
Я строю очень простой, но функциональный и при этом бескомпромиссно троичный вычислитель, основанный на сбалансированной троичной системе счисления. Весь компьютер будет построен только на базе троичных мультиплексоров, которые собраны из аналоговых ключей. Следите за мини-сериалом о постройке моего вычислителя на ютубе:

Скоро 22е апреля, да не просто так, а 2020 го года. Каждый советский школьник должен был знать, что это за праздник 22 го апреля. Однажды, когда я был в первом классе, наша учительница спросила ласковым голосом, что за праздник сегодня. Увидев, что моя соседка по парте, Оля Пенкина, заёрзала, учительница задала вопрос именно ей: «Оленька, знаешь ли ты, какой сегодня праздник?» На что Оля потупилась и сказала: «День моего рождения». Мне было понятно, что день рождения Оли Пенкиной тут совершенно ни при чём (тем более, что Оля зажала принести конфет на весь класс), а разговор идёт о дне рождения дедушки Ленина. Учительница настолько растерялась, что я этот момент отчётливо помню до сих пор. Итак, 22 го апреля этого года исполнится сто пятьдесят лет со дня рождения Владимира Ильича.
Но есть и третье важное событие (после дней рождения Оли Пенкиной и Володи Ульянова), произошедшее 22 го апреля, о котором я узнал гораздо, гораздо позже. 22 го апреля 1970 го года увидел свет компьютер Сетунь-70. Итак, коллеги, буквально на днях будет большой юбилей, пятьдесят лет второй версии Сетуни.
Чтобы отметить это знаменательное событие, я решил снять первый сезон мини-сериала о постройке троичного вычислителя. Для того, чтобы понять что происходит, совсе не обязательно разбираться в электронике, достаточно немного здравого смысла и знания арифметики на уровне пятого класса. Лично я в электронике не понимаю строгим счётом ничего, но мне это не мешает, ведь у меня же ардуино головного мозга! Я паяльник впервые в руки взял ровно для этого проекта. И вы знаете, если запаять восемь сотен корпусов микросхем, то навык волшебным образом прокачивается! Сейчас мой монтаж выглядит примерно так:

Итак, поехали!
Самым первым делом я расскажу о том, как работает плата ввода-вывода, та, что из гетинакса на вот этой фотографии:

Почему я начал именно с этой платы? Потому что она играет одновременно роль и клавиатуры, и монитора для моего вычислителя. Практически все особенности работы моего вычислителя я буду иллюстрировать при помощи этой платы, так что важно понять, что именно она делает, благо это просто. На этой плате расположено девять независимых линий ввода-вывода, которые схематически выглядят следующим образом:
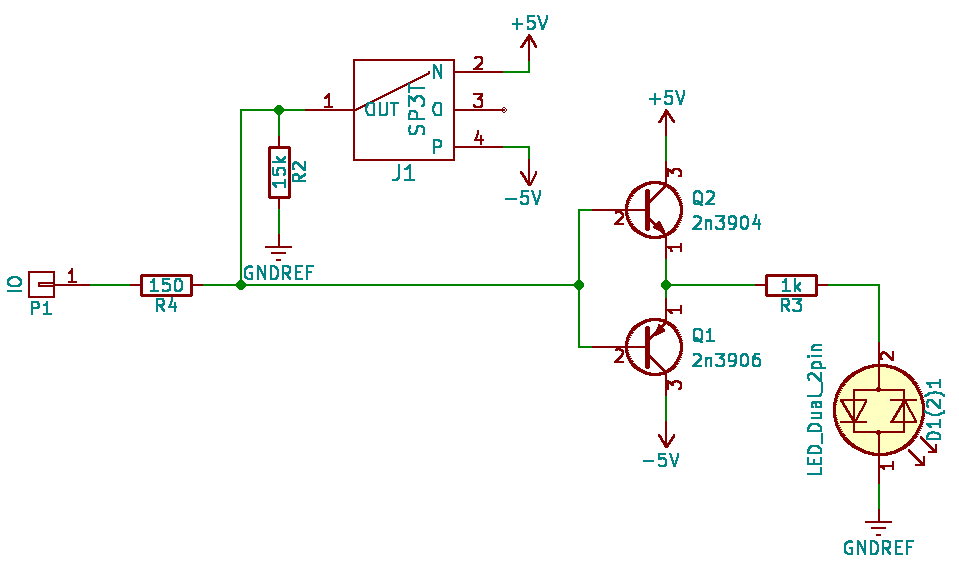
Каждый ввод-вывод несёт на себе один трёхпозиционный переключатель, который в режиме «клавиатуры» может выдать на линию одно из трёх возможных напряжений: -5, 0 или +5 вольт.
А что с режимом «монитора»? К каждой линии у меня подключен двуцветный светодиод, таким образом, если у нас на линии +5 В, то диод горит зелёным, если -5 В, то красным, ну, а если 0 В, то диод погашен. В среднем положении переключателя линия слабо подтянута к 0 В, и тогда входящий сигнал перетянет слабую подтяжку к 0 В. Эмиттерный повторитель обеспечивает надёжную индикацию даже самых слабых сигналов.
На гетинаксе плата выглядит как-то так:

Плата предназначена для лёгкого воспроизведения дома даже такими кривыми руками, как у меня: она однослойная и не содержит ни одной перемычки.
Вот самая первая серия моего сериала:
Сбалансированная троичная система — это необычная, но математически довольно красивая система счисления. Она имеет свойство, что все числа могут быть представлены в единой нотации; не нужен знак минус, чтобы указать на то, что «это число отрицательное». Если вам нравится играть с числами, вероятно, вам понравится.
В десятичной системе счисления используются десять цифр, от 0 до 9, соглашение, при котором каждая позиция в числе стоит в десять раз больше значения позиции справа от нее. Так, например, число 7204 обозначает «семь тысяч, две сотни, без десятков и четыре». Точно так же стандартная позиционная троичная система использует три цифры, обычно 0, 1 и 2, и соглашение, при котором каждая позиция в числе стоит в три раза больше значения позиции справа от нее.

— Жуткий кошмар! Нули и единицы повсюду. И кажется, я видел двойку.
— Это просто сон, Бендер. Двоек не бывает.
Хреновый из меня художник, давайте про арифметику лучше. Несмотря на троичность, двойки не существует! В сбалансированной троичной системе три цифры имеют значения 0, 1 и -1. Чтобы избежать неудобства использования двух символов, '-' и 1, для обозначения цифр, будем использовать символы N, O и P. Как и в вышеприведенном примере, тогда число PONP обозначает «один раз 27, ни одной девятки, минус одна тройка, и одна единица».
В сбалансированной троичной системе, равно как и в более привычных позиционных системах счисления, существует ровно один способ представления любого (целого) числа. В отличие от привычных систем, нет необходимости в дополнительном символе, указывающем на то, что число является отрицательным; например, -5 представлено в виде NPP: -9 + 3 + 1.
Чуть подробнее об этом во втором эпизоде первого сезона:
А теперь мы поговорим о крайне важной вещи: о троичных мультиплексорах. Эта тема особенно важна тем, что троичный мультиплексор является базовым блоком, из которого будет построено абсолютно всё остальное.
Логически троичный мультиплексор может быть представлен как блок с пятью выводами, которые я назову S, N, O, P и C. Это очень просто, вот этот переключатель, который я позаимствовал из электрического конструктора своего сына-дошкольника — это самый настоящий троичный мультиплексор-демультиплексор!

Линия S (селектор) работает только на вход, и может принимать одно из трёх возможных состояний,
которые на нашем переключателе соответствуют трём разным положениям. В зависимости от линии S мы замыкаем линию C с одной из линий N, O или P.
Схематически такие мультиплексоры обозначают как-то так:
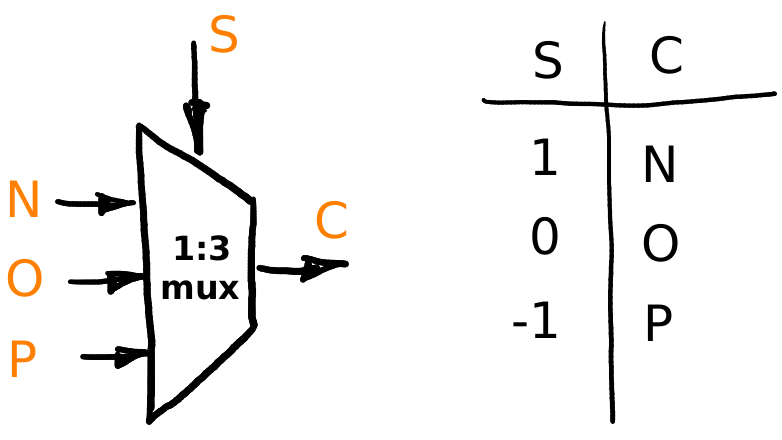
Всем хорош наш мультиплексор, но есть у него один недостаток — надо селектор руками переставлять, что сводит на нет смысл постройки вычислителя. Давайте избавляться от механики, перейдём на чистую электронику.
Вариантов изготовления электронного троичного мультиплексора масса, но мне больше всего приглянулся вариант, предложенный Shaos. Он использует аналоговые ключи dg403, которые, будучи подключены вот таким образом, позволяют получить два троичных мультиплексора:
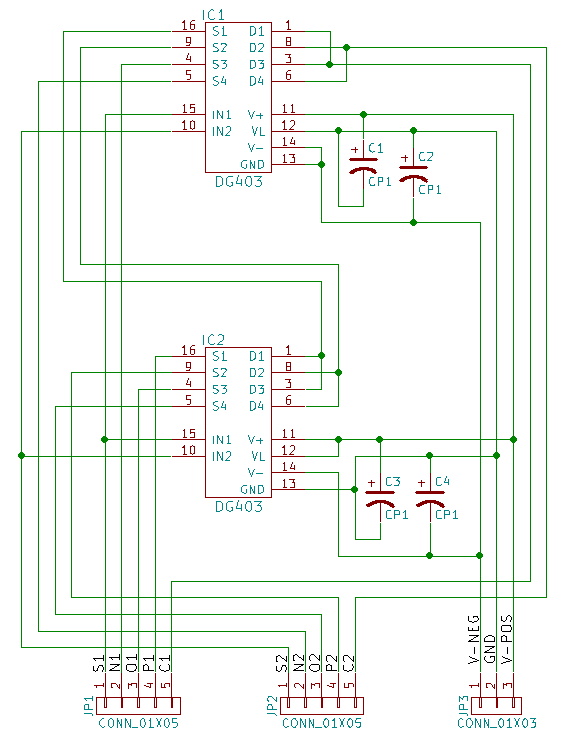
А вот так оно выглядит в железе, эта платка называется тримукс:

У него 13 выводов: три на биполярное питание для ключей, и два набора по пять линий S, N, O, P и C, поскольку на такой плате у нас два независимых мультиплексора. Таких треугольных платок в моём вычислителе будет изрядное количество, я запаял восемь сотен корпусов dg403 (я не псих!), то есть, у меня в распоряжении восемьсот мультиплексоров (четыреста тримуксов).
Смотрим третью серию!
В четвёртом эпизоде я рассказываю о постройке первого вменяемого устройства, а именно — ячейки памяти, которая будет хранить один трит информации. Схематически ячейка памяти выглядит вот так:
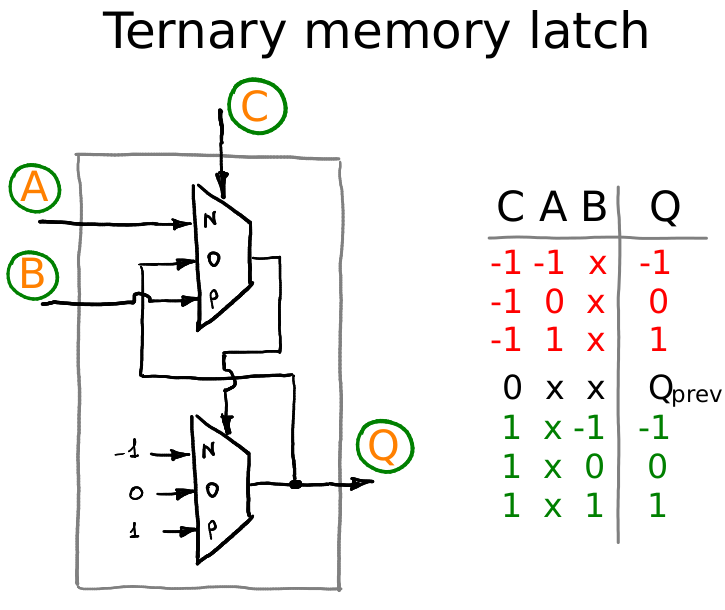
Поскольку в одном тримуксе у нас два мультиплексора, то из одного тримукса можно получить одну ячейку памяти:

Это статическая ячейка памяти с запоминанием по уровню. У неё четыре вывода: A, B, C и Q. Линии направленные, A, B и C работают на вход, ну, а линия Q на выход. Смотрите, если на вход C подать минус единицу, то выход Q будет повторять сигнал с линии A:

Если же на вход C подать единицу, то выход Q будет повторять сигнал с линии B, игнорируя при этом линию A:
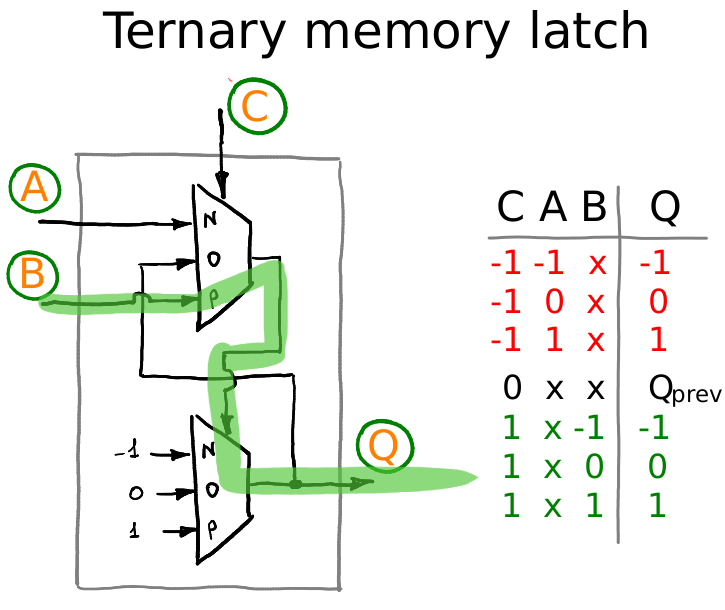
А что будет, если на вход C подать логический ноль? А тогда получится, что внутри нашей схемы сигнал с выхода Q закольцовывается, таким образом запоминая ту информацию, которая была в памяти ровно перед тем моментом, когда селектор C переключился в ноль. Теперь я могу изменять линии записи A и B как хочу, это никак не влияет на то, что записано в нашу ячейку памяти :
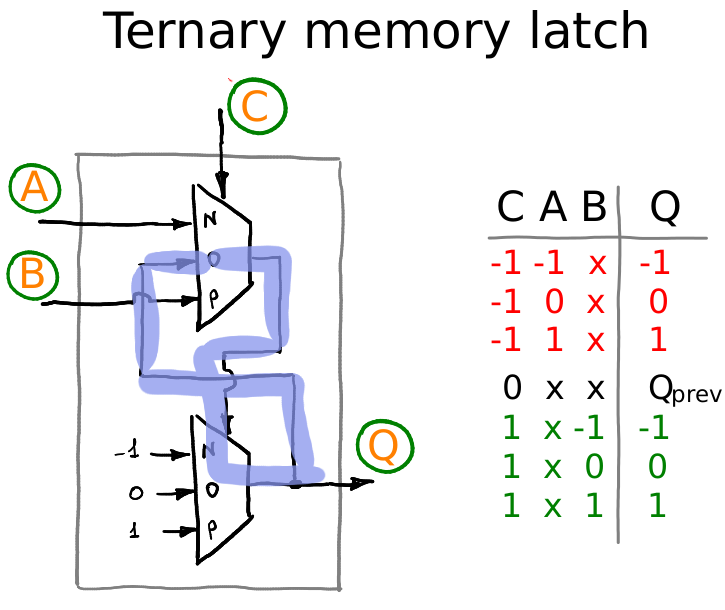
Эта ячейка памяти прекрасно запоминает информацию в зависимости от уровня сигнала C, но мне будет удобнее, если сигналом к запоминанию будет не сам уровень, но его изменение. То есть, я хочу, чтобы моя память сохраняла информацию по фронту сигнала на линии клока. Не беда, это совсем нетрудно сделать.
Мы можем позаимствовать много идей из двоичного мира. Там ровно эта задача уже решена.
Если взять две одинаковые двоичные защёлки, то собрав их в каскад, можно получить D-флип-флоп. Двоичный триггер с управлением по уровню называется gated D-latch. Грубо говоря, у него есть два входа: D (данные) и E (enable). Единственный выход Q равен D если E=1, и сохраняет своё значение если E=0.
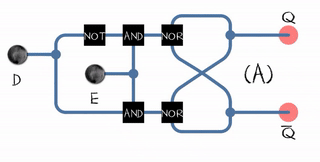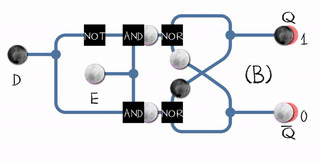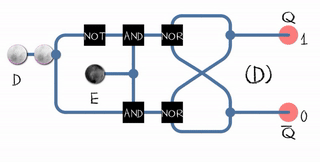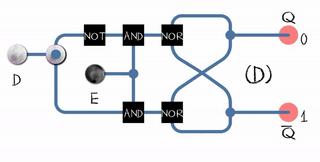
Триггер со срабатыванием по фронту (flip-flop) может быть построен из двух обычных защёлкок (gated D-latch) и одного инвертера:
Эта схема называется Master-slave edge-triggered D flip-flop.
Ну, а я что, рыжий? Давайте сделаем ровно так же, собрав две одинаковые ячейки во флип-флап-флоп!

Если соединить две ячейки как показано на этой схеме, то запоминание информации будет происходить по двум ниспадающим фронтам PO и ON. Давайте скажем, что я хочу записать в память минус единицу. Я подаю -5 вольт на линию A, когда клок переходит в единицу, выход ведущей защёлки получает значение из линии записи. Но как только клок переходит в ноль, то ведущая защёлка уже запомнила значение, и линия записи теперь игнорируется. И при дальнейшем движении клока произойдёт копирование информации из ведущей в ведомую защёлку.
В четвёртой серии я рассказываю, как устроен модуль памяти, который может запомнить трёхтритное число, он как раз на превьюшке эпизода:
Ну и венчает первый сезон сериала плата памяти с произвольным доступом:

Схематически её можно представлять следующим образом:
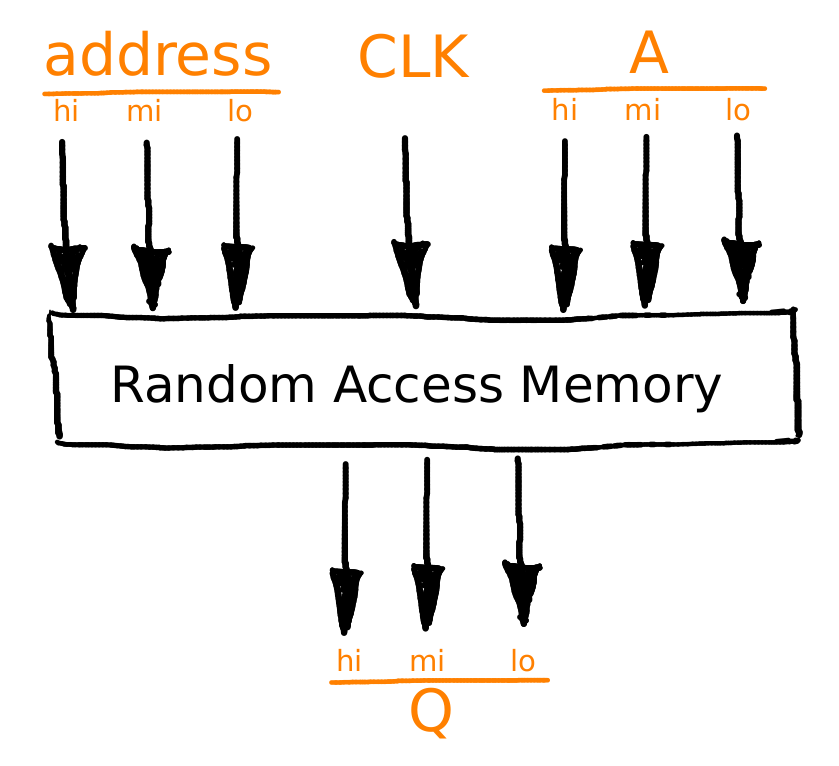
Три линии адреса выбирают нужную ячейку памяти, три линии A подают трёхтритное число на запись в память, а три линии Q говорят, что именно сейчас в память записано. Ну и тактирующий сигнал, который подаёт команду записи.
Итак, слева внизу на моей на моей плате видны 13 трёхтритных модулей памяти, которые были разобраны в предыдущем эпизоде. А как происходит адресация? Очень просто, давайте рассмотрим троичный мультиплексор 1-к-13:
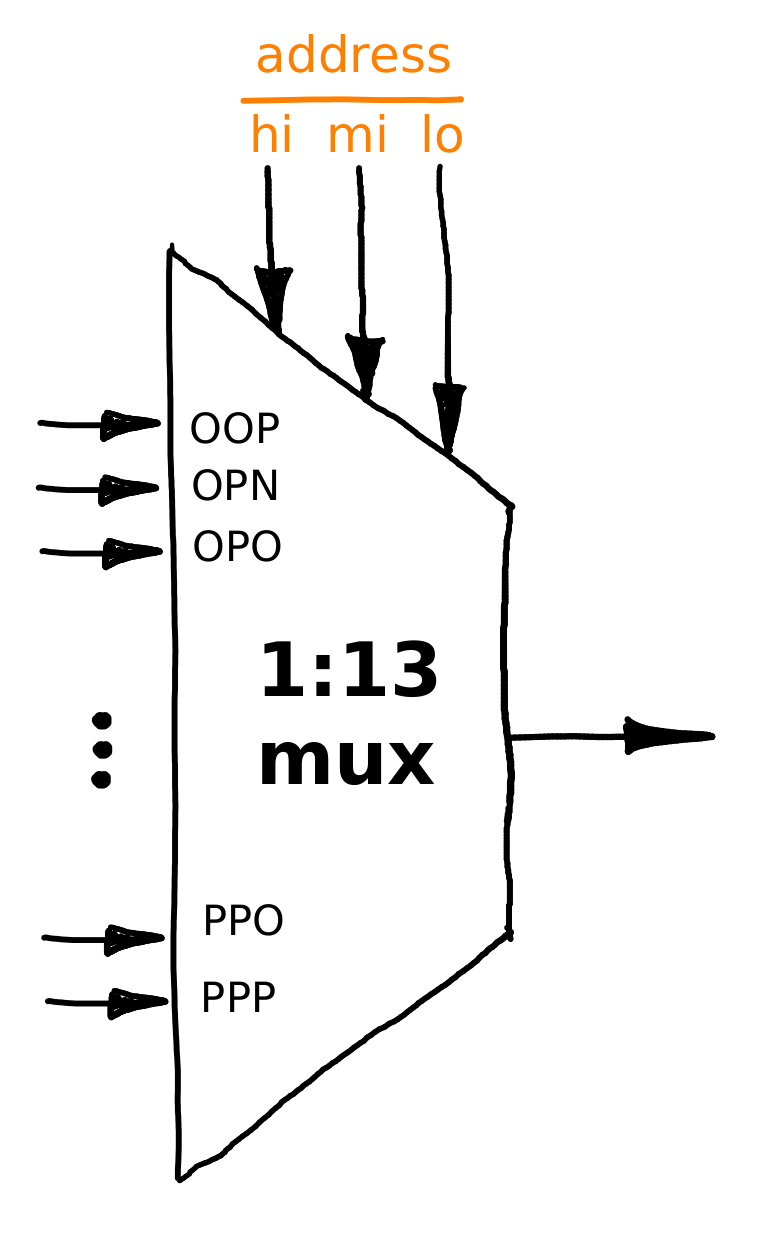
Он очень похож на обычный троичный мультиплексор, единственная разница — у него входных каналов не 3, а 13, и линия селектора трёхтритная.
Обратите внимание, что при помощи трёхтритного адреса мы можем адресовать 27 разных ячеек, в то время как моё запоминающее устройство имеет только 13. Поэтому все адреса, меньшие либо равные единице, выбирают первую ячейку памяти. Этот мультиплексор 1:13 — просто урезанная версия мультиплексора 1:27:
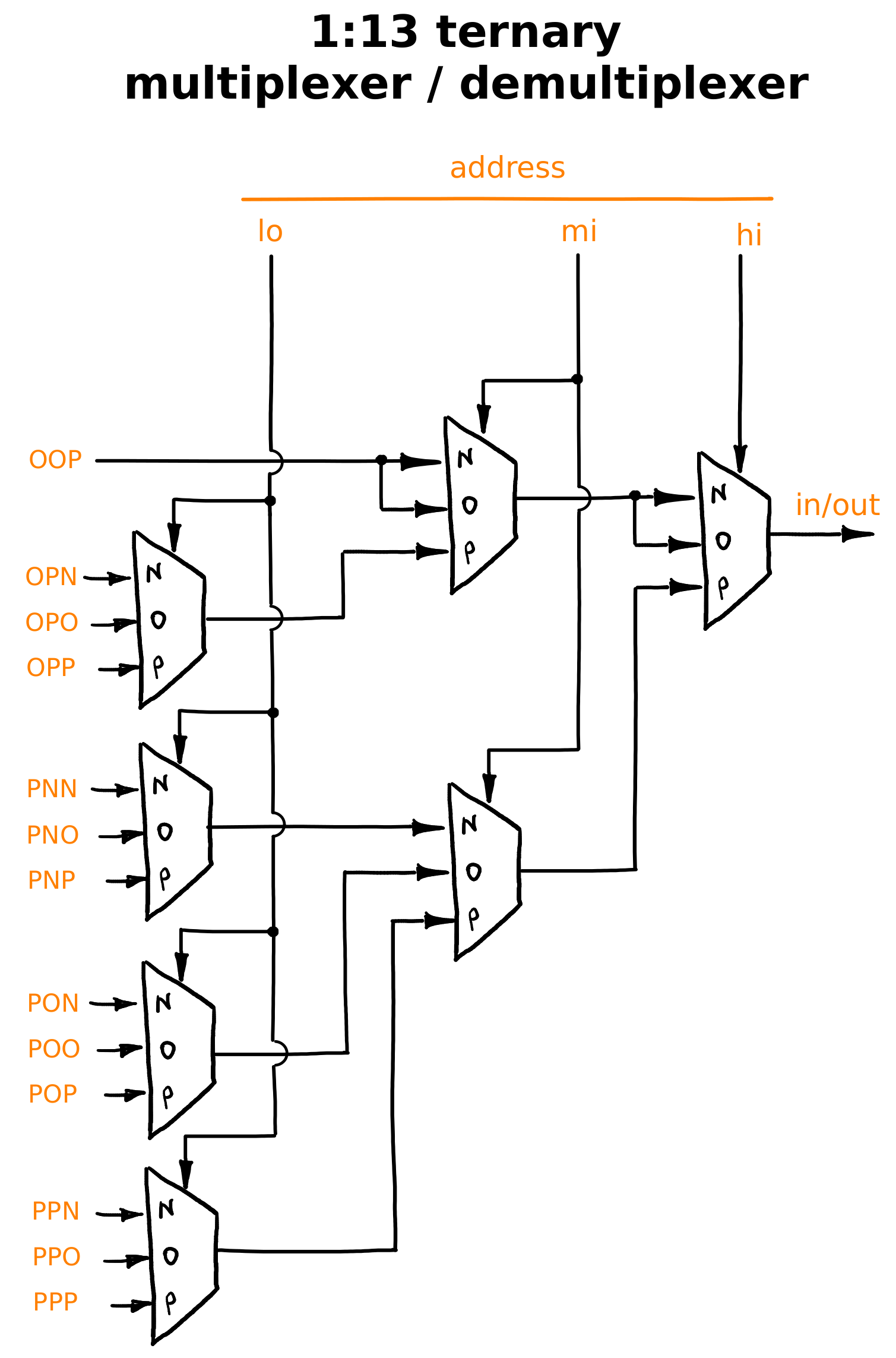
Итак, на моей плате семь таких мультиплексоров 1:13. Какова их функция? Возьмём, например, тактирующий сигнал, входящий на запоминающее устройство. Вполне очевидно, что этот сигнал должен попасть не на все тринадцать ячеек памяти, но только на выбранную. Поэтому тринадцать линий клока заведены в этот мультиплексор, и я коммутирую входящий клок в нужную ячейку. Ровно так же нам нужно три линии на сигнал A и три линии на сигнал Q.
Ну и последняя нерассмотренная вещь на плате памяти — это белая плата в левом верхнем углу фотографии. Это мой страшный сон, я её разводил очень долго. На ней нет ни одного активного элемента, это просто провода и ничего больше. Её задача — соединить правильные линии ячеек памяти с нужными линиями мультиплексоров 1:13. Делать это проводами я бы просто застрелился. 151 провод без ошибок монтажа мне не по силам!

Итак, давайте я вам покажу эту плату памяти в действии:
На этом первый сезон минисериала завершился, по мере готовности железа я буду снимать продолжение. В следующем сезоне мы поговорим о системе команд моего вычислителя, а также об арифметико-логическом устройстве.
Если вам понравилось, то чтобы скрасить ожидание следующего сезона, вы можете попробовать свои силы в программировании Триадора уже сейчас, я специально для этого подготовил эмулятор.
С днём Космонавтики и до новых встреч в эфире!
