Метрика в машинном обучении сложных систем, алгоритм и программный код
Для решения задач машинного обучения предлагается метрика, основанная на формуле отношения сигнала к шуму, SNR:
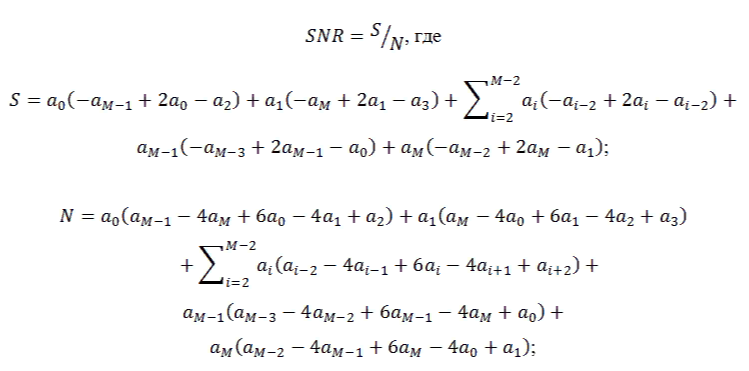
Для приложений в сфере информационных технологий, измерительной технике, где существует проблема выбора объективного количественного критерия помехоустойчивости устройств применяется отношение сигнала к шуму, SNR.
Предложенная формула SNR инвариантна относительно любых линейных преобразований наборов a (i) (инвариантность по масштабу и сдвигу) и не зависит от числа гранулирования M для множества точек нормального гауссова распределения. Квадратичные формы S и N положительно определены для произвольных наборов a (i).
Вывод формулы осуществляется из фрактала «пыль Кантора». Из вывода формулы и опыта применения, уместно приложение в сложной системе, когда упорядоченность причинно-следственных связей элементов внутри сложной системы не значима, а заметны нелинейные тенденции к самоорганизации данных.
Отношение сигнала к шуму обратно пропорционально числу степеней свободы сложной системы. Характерны для системы максимальные и минимальные значения SNR, последовательное их чередование.
Для применения метрики в машинном обучении критически важна оптимизация по времени расчёта. Исходя из опыта, предлагается следующий программный продукт.
# SNR, автор Александр Макарик(с)
import numpy as np
from numba import njit
@njit(fastmath=True)
def calcChisl(m):
n=m.size-1
s=0
for i in range (2, n - 1):
s = s + m[i] * (2 * m[i] - m[i + 2] - m[i - 2])
#'s = s + massivOfElements(i] * (massivOfElements2(i] - massivOfElements(i + 2] - massivOfElements(i - 2])
#'для замкнутого контура
s = s + m[0] * (2 * m[0] - m[2] - m[n - 1])
s = s + m[1] * (2 * m[1] - m[3] - m[n])
s = s + m[n - 1] * (2 * m[n - 1] - m[0] - m[n - 3])
s = s + m[n] * (2 * m[n] - m[1] - m[n - 2])
return s
@njit(fastmath=True)
def calcZnam(m):
n=m.size-1
s=0
for i in range (2, n - 1):
s = s + m[i] * (6 * m[i] - 4 * m[i + 1] + m[i + 2] + m[i - 2] - 4 * m[i - 1])
# 's = s + massivOfElements(i] * (massivOfElements6(i] - massivOfElements4(i + 1] + massivOfElements(i + 2] + massivOfElements(i - 2] - massivOfElements4(i - 1])
#'для замкнутого контура
s = s + m[0] * (6 * m[0] - 4 * m[1] + m[2] + m[n - 1] - 4 * m[n])
s = s + m[1] * (6 * m[1] - 4 * m[2] + m[3] + m[n] - 4 * m[0])
s = s + m[n - 1] * (6 * m[n - 1] - 4 * m[n] + m[0] + m[n - 3] - 4 * m[n - 2])
s = s + m[n] * (6 * m[n] - 4 * m[0] + m[1] + m[n - 2] - 4 * m[n - 1])
# 'для незамкнутого контура
# 's = s + m(1] * (3 * m(1] - 4 * m(2] + m(3])
# 's = s + m(2] * (7 * m(2] - 4 * m(1] + -4 * m(3] + m(4])
# 's = s + m(n - 1] * (7 * m(n - 1] - 4 * m(n - 2] - 4 * m(n] + m(n - 3])
# 's = s + m(n] * (3 * m(n] - 4 * m(n - 1] + m(n - 2])
return s
def calcSNR(arr):
#print(arr[0:10])
z=calcZnam(arr)
#if z!=0:
a=calcChisl(arr)/z
#else:
# a=0
if a<0:print ('znam=',znam)
if a<0:print ('Chisl=',znam)
return a
def snrVectorSlow(arr,deslength):
vSNR=np.zeros(arr.size-deslength)
for i in range(arr.size-deslength):
b=arr[i:i+deslength]
# vSNR = np.append(vSNR, SNR.calcSNR(b])
vSNR[i]= calcSNR(b)
return vSNR
@njit(fastmath=True)
def snrChislVector(m):
chisl=np.zeros(m.size)
n=m.size-1
for i in range (2, n - 1):
chisl[i] = m[i] * (2 * m[i] - m[i + 2] - m[i - 2])
#'s = s + massivOfElements(i] * (massivOfElements2(i] - massivOfElements(i + 2] - massivOfElements(i - 2])
#'для замкнутого контура
chisl[0] = m[0] * (2 * m[0] - m[2] - m[n - 1])
chisl[1] = m[1] * (2 * m[1] - m[3] - m[n])
chisl[n-1] = m[n - 1] * (2 * m[n - 1] - m[0] - m[n - 3])
chisl[n] = m[n] * (2 * m[n] - m[1] - m[n - 2])
return chisl
@njit(fastmath=True)
def snrZnamVector(m):
n=m.size-1
k=m
tempV=np.zeros(m.size)
for i in range (2, n - 1):
tempV[i] = k[i] * (6 * k[i] - 4 * k[i + 1] + k[i + 2] + k[i - 2] - 4 * k[i - 1])
tempV[0] = k[0] * (6 * k[0] - 4 * k[1] + k[2] + k[n - 1] - 4 * k[n])
tempV[1] = k[1] * (6 * k[1] - 4 * k[2] + k[3] + k[n] - 4 * k[0])
tempV[n - 1] = k[n - 1] * (6 * k[n - 1] - 4 * k[n] + k[0] + k[n - 3] - 4 * k[n - 2])
tempV[n] = k[n] * (6 * k[n] - 4 * k[0] + k[1] + k[n - 2] - 4 * k[n - 1])
znam=tempV #*9
return znam
@njit(fastmath=True)
def snrVector(arr,deslength):
vSNR=np.zeros(arr.size-deslength)
b=arr[0:deslength]
chisl=snrChislVector(b)
znam=snrZnamVector(b)
vSNR[0]=np.sum(chisl)/np.sum(znam)
n=deslength-1
#d=arr[0:deslength]
for k in range(1,arr.size-deslength):
if (k%1000==0):print(k)
d=arr[k:k+deslength]
#chisl=np.delete(chisl,0)
chisl=chisl[1:chisl.size] #так быстрее
chisl = np.append(chisl, 0) # просто в конец добавляем элемент
chisl[1] = d[1] * (2 * d[1] - d[3] - d[n])
i = n - 2
chisl[i] = d[i] * (2 * d[i] - d[i + 2] - d[i - 2])
chisl[n - 1] = d[n - 1] * (2 * d[n - 1] - d[0] - d[n - 3])
chisl[n] = d[n] * (2 * d[n] - d[1] - d[n - 2])
znam=znam[1:znam.size] #так быстрее
znam = np.append(znam, 0) # просто в конец добавляем элемент
znam[0] = d[0] * (6 * d[0] - 4 * d[1] + d[2] + d[n - 1] - 4 * d[n])
znam[1] = d[1] * (6 * d[1] - 4 * d[2] + d[3] + d[n] - 4 * d[0])
znam[i] = d[i] * (6 * d[i] - 4 * d[i + 1] + d[i + 2] + d[i - 2] - 4 * d[i - 1])
znam[n - 1] = d[n - 1] * (6 * d[n - 1] - 4 * d[n] + d[0] + d[n - 3] - 4 * d[n - 2])
znam[n] = d[n] * (6 * d[n] - 4 * d[0] + d[1] + d[n - 2] - 4 * d[n - 1])
vSNR[k]=np.sum(chisl)/np.sum(znam)
return vSNR
@njit(fastmath=True)
def snrVectorFastest(arr,deslength):
vSNR=np.zeros(arr.size-deslength)
d=arr[0:deslength]
chisl=np.sum(snrChislVector(d))
znam=np.sum(snrZnamVector(d))
kkk=chisl/znam
vSNR[0]=kkk
n=deslength-1
v=np.zeros(6)
# chisl[i] = m[i] * (2 * m[i] - m[i + 2] - m[i - 2])
for k in range(1,arr.size-deslength):
# if (k%1000==0):print(k)
v[0] = d[0] * (2 * d[0] - d[2] - d[n-1])
v[1] = d[1] * (2 * d[1] - d[3] - d[n])
v[2] = d[2] * (2 * d[2] - d[4] - d[0]) #его не обязательно...cчитать потом
i = n - 2
# v[3] = d[i] * (2 * d[i] - d[i + 2] - d[i - 2]) #его удалять не надо...!!! но добавить надо
v[4] = d[n - 1] * (2 * d[n - 1] - d[0] - d[n - 3])
v[5] = d[n] * (2 * d[n] - d[1] - d[n - 2])
chisl=chisl-v[0]-v[1]-v[2]-v[4]-v[5]
#tempV[i] = k[i] * (6 * k[i] - 4 * k[i + 1] + k[i + 2] + k[i - 2] - 4 * k[i - 1])
v[0] = d[0] * (6 * d[0] - 4 * d[1] + d[2] + d[n - 1] - 4 * d[n])
v[1] = d[1] * (6 * d[1] - 4 * d[2] + d[3] + d[n] - 4 * d[0])
v[2] = d[2] * (6 * d[2] - 4 * d[3] + d[4] + d[0] - 4 * d[1]) #его не обязательно считать потом
# v[3] = d[i] * (6 * d[i] - 4 * d[i + 1] + d[i + 2] + d[i - 2] - 4 * d[i - 1]) #его удалять не надо...но добавить надо
v[4] = d[n - 1] * (6 * d[n - 1] - 4 * d[n] + d[0] + d[n - 3] - 4 * d[n - 2])
v[5] = d[n] * (6 * d[n] - 4 * d[0] + d[1] + d[n - 2] - 4 * d[n - 1])
znam=znam-v[0]-v[1]-v[2]-v[4]-v[5]
d=arr[k:k+deslength]
v[0] = d[0] * (2 * d[0] - d[2] - d[n-1])
v[1] = d[1] * (2 * d[1] - d[3] - d[n])
v[3] = d[i] * (2 * d[i] - d[i + 2] - d[i - 2]) #его удалять не надо...!!! но добавить надо
v[4] = d[n - 1] * (2 * d[n - 1] - d[0] - d[n - 3])
v[5] = d[n] * (2 * d[n] - d[1] - d[n - 2])
chisl=chisl+ v[0] + v[1]+v[3]+v[4]+v[5]
v[0] = d[0] * (6 * d[0] - 4 * d[1] + d[2] + d[n - 1] - 4 * d[n])
v[1] = d[1] * (6 * d[1] - 4 * d[2] + d[3] + d[n] - 4 * d[0])
#v[2] = d[2] * (6 * d[2] - 4 * d[3] + d[4] + d[0] - 4 * d[1]) #его не обязательно считать потом
v[3] = d[i] * (6 * d[i] - 4 * d[i + 1] + d[i + 2] + d[i - 2] - 4 * d[i - 1]) #его удалять не надо...но добавить надо
v[4] = d[n - 1] * (6 * d[n - 1] - 4 * d[n] + d[0] + d[n - 3] - 4 * d[n - 2])
v[5] = d[n] * (6 * d[n] - 4 * d[0] + d[1] + d[n - 2] - 4 * d[n - 1])
znam=znam + v[0] + v[1]+v[3]+v[4]+v[5]
vSNR[k]=chisl/znam
return vSNR