Memento Mori или вычисляем «магические квадраты» 5x5
Привет Хабр.
Примерно год назад я рассматривал тему использования GPU на примере вычисления «магических квадратов» 4×4. Там все довольно-таки очевидно, этих квадратов всего 7040, и вычислить их можно практически на чем угодно, хоть на Ардуине (но это не точно). Аналогичным способом я решил найти все квадраты 5×5, и результаты оказались весьма интересными, забегая вперед, скажу сразу, найти их я так и не смог.
Если кому интересно, подробности решения пятничной «несложной задачи» под катом.

Чтобы не повторяться, для тех кто плохо помнит, что такое «магический квадрат» и как его находить, советую прочитать первую часть. В частном случае, квадрат 5×5 это поле из 25 ячеек, в которые вписаны цифры от 1 до 25, так что суммы каждой горизонтали, вертикали и диагонали равны. Пример такого квадрата показан на картинке выше.
Поиск «магического квадрата» интересен для программирования тем, что с одной стороны, задача является весьма простой и понятной даже школьнику, с другой стороны, она является довольно-таки нетривиальной в плане объема вычислений, и открывает большой простор для разных оптимизаций. Эту задачу можно решать и на 1 м, и на 2 м и на 20 м году программирования, и каждый раз найти для себя что-то новое. Итак, приступим.
С/С++
Первый вариант будет самым простым, безо всякой многопоточности. Идея кода весьма тривиальна — берем первое число из множества 1…25, затем второе число из всех кроме первого, и так далее. Крайние числа из правой и нижней колонок перебирать не нужно, т.к. они вычисляются из имеющихся.
На С++ это можно легко записать с помощью std: set:
const int N=5, S = 65, MAX=N*N;
std::set mset = { 1,2,3,4,5, 6,7,8,9,10, 11,12,13,14,15, 16,17,18,19,20, 21,22,23,24,25 };
for(auto x11 : mset) {
std::set set12(mset);
set12.erase(x11);
for(auto x12 : set12) {
std::set set13(set12);
set13.erase(x12);
for(auto x13 : set13) {
if (x11 + x12 + x13 >= S-2) continue;
std::set set14(set13);
set14.erase(x13);
for(auto x14 : set14) {
elem x15 = S - x11 - x12 - x13 - x14;
if (x15 < 1 || x15 > MAX || x15 == x11 || x15 == x12 || x15 == x13 || x15 == x14) continue;
...
}
}
}
Запускаем, все работает, но как-то медленно. Чисто для интереса, пишу код «втупую» на С, безо всяких std, просто проверяя в каждом цикле, что переменная уже использовалась.
for(elem x11=1; x11<=MAX; x11++) {
for(elem x12=1; x12<=MAX; x12++) {
if (x12 == x11) continue;
for(elem x13=1; x13<=MAX; x13++) {
if (x13 == x11 || x13 == x12) continue;
if (x11 + x12 + x13 >= S-2) continue;
for(elem x14=1; x14<=MAX; x14++) {
...
}
}
}
Я конечно, понимаю, что реализация sdt: set не так уж проста, но чтобы до такой степени… Разница во времени исполнения 12.0 и 0.35с — Си-код работает быстрее в 34 раза!
Идем дальше. Попробуем оценить, сколько займет расчет целиком. Для упрощения задачи разобьем квадрат на две части. Верхние две строки квадрата максимально имели бы 25×24*23×22*21×20*19×18 = 43.609.104.000 вариантов расстановки чисел, но поскольку мы отбрасываем часть вариантов с неподходящей суммой, остается «всего лишь» 8.340.768.000. Теперь рассмотрим две оставшиеся (3ю и 4ю) строки. Несложное профилирование показало, что перебор строк с проверками суммы занимает 1.48с. Итого, умножив одно на другое, получаем что время проверки всех «магических квадратов» 5×5 составит 391 год. Это правда, без многопоточности, но тут она нас не спасет — сколько там ядер в CPU, в лучшем случае 16? Даже если ускорить вычисление в 16 раз, окончания я пожалуй, все равно не дождусь. Пора переходить к NVIDIA CUDA.
NVIDIA CUDA
Принцип вычислений на видеокарте по сути, прост. В CUDA «железо» видеокарты делится на множество блоков, каждый блок может иметь несколько потоков. Весь бонус состоит в том, что блоков этих много, и они могут делать вычисления параллельно.
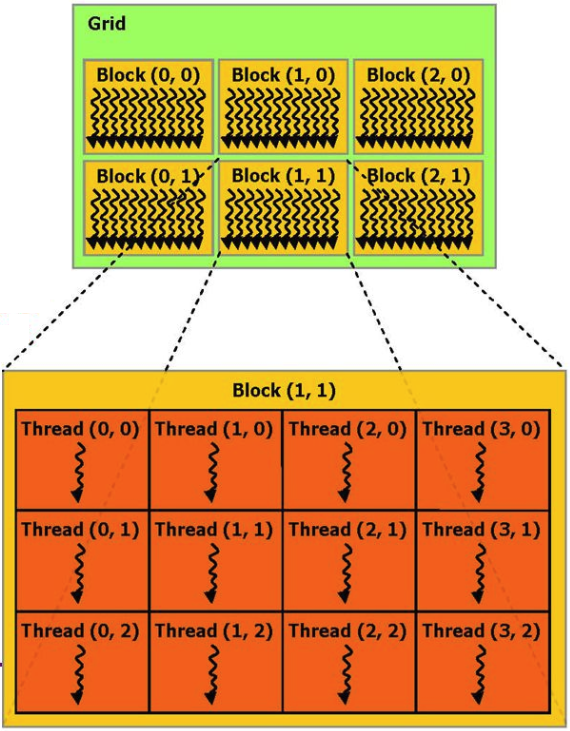
Логически, блоки могут адресовываться как 1D, 2D или 3D массив, внутри каждого блока адресация потоков также может быть сделана как 1D, 2D или 3D. Как показал эксперимент, CUDA вполне позволяет выделить 25×25x25 = 15625 блоков, при 25×25 = 625 процессов на каждый блок. Максимальные ограничения указаны в спецификации CUDA.
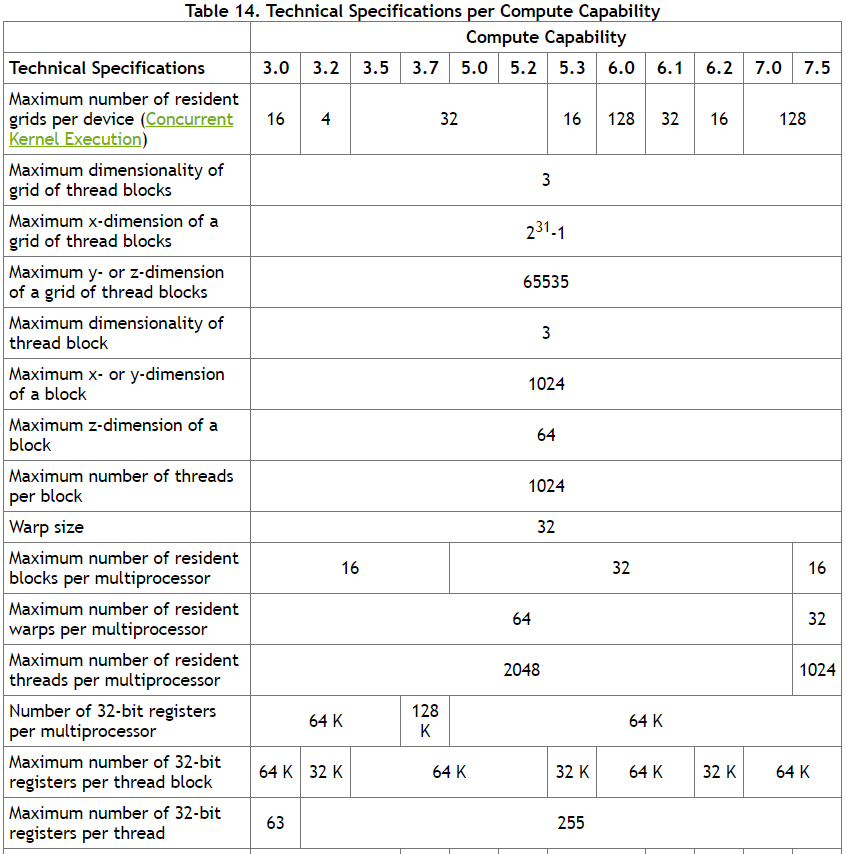
Разумеется, в реале, 15625×625 = 9 млн процессов видеокарта параллельно не запустит — по крайней мере, явно не та, которая стоит у меня в ПК. Но можно надеяться, что драйвер NVIDIA обеспечит загрузку ядер по-максимуму, взяв всю работу по распараллеливанию на себя.
Таким образом, логика кода получается довольно простой — внешний цикл, подсчитывающий первые 16 чисел магических квадратов, мы перебираем на CPU, а внутренний цикл «отдаем» видеокарте, которая (теоретически) должна сделать расчет заметно быстрее. Каждый поток будет делать достаточно простой расчет со всего тремя вложенными циклами. Важно еще иметь в виду, что видеокарта работает со своей памятью, так что перед запуском расчета данные туда нужно положить, а по окончании расчета, забрать результаты обратно.
Код я здесь не привожу, чтобы не загромождать текст, ссылка на исходники в конце статьи.
Результаты
Результаты, разумеется, зависят от видеокарты. Код был протестирован на 2х ПК — ноутбуке с GeForce GTX 950M и десктопе с GeForce GTX 1060.
GTX 950M
Внутренний цикл, который в CPU-варианте выполнялся за 1.48с, с помощью GPU был выполнен за… 0.5с. Увы, прирост составил всего 3 раза. Видимо, 625 потоков на ядро все же большая нагрузка для ноутбучной видеокарты, и накладные расходы превышают плюсы от распараллеливания. Интересно, что попытки поменять количество потоков и блоков в разных пропорциях результата не улучшили — если вынести часть кода в CPU, то GPU вычисления выполняются быстрее, зато остальное делается медленнее. В общем, драйвер NVIDIA, похоже, действительно делает свою работу по распараллеливанию задач весьма неплохо.
Результат работы программы показан на скриншоте.

Как можно видеть, первый «магический квадрат» был найден за 680с, а окончательных результатов расчета я скорее всего, не дождусь, если конечно медицина не сделает какой-то реальный шаг вперед ;)
GTX 1060M
Тут все заметно пободрее:
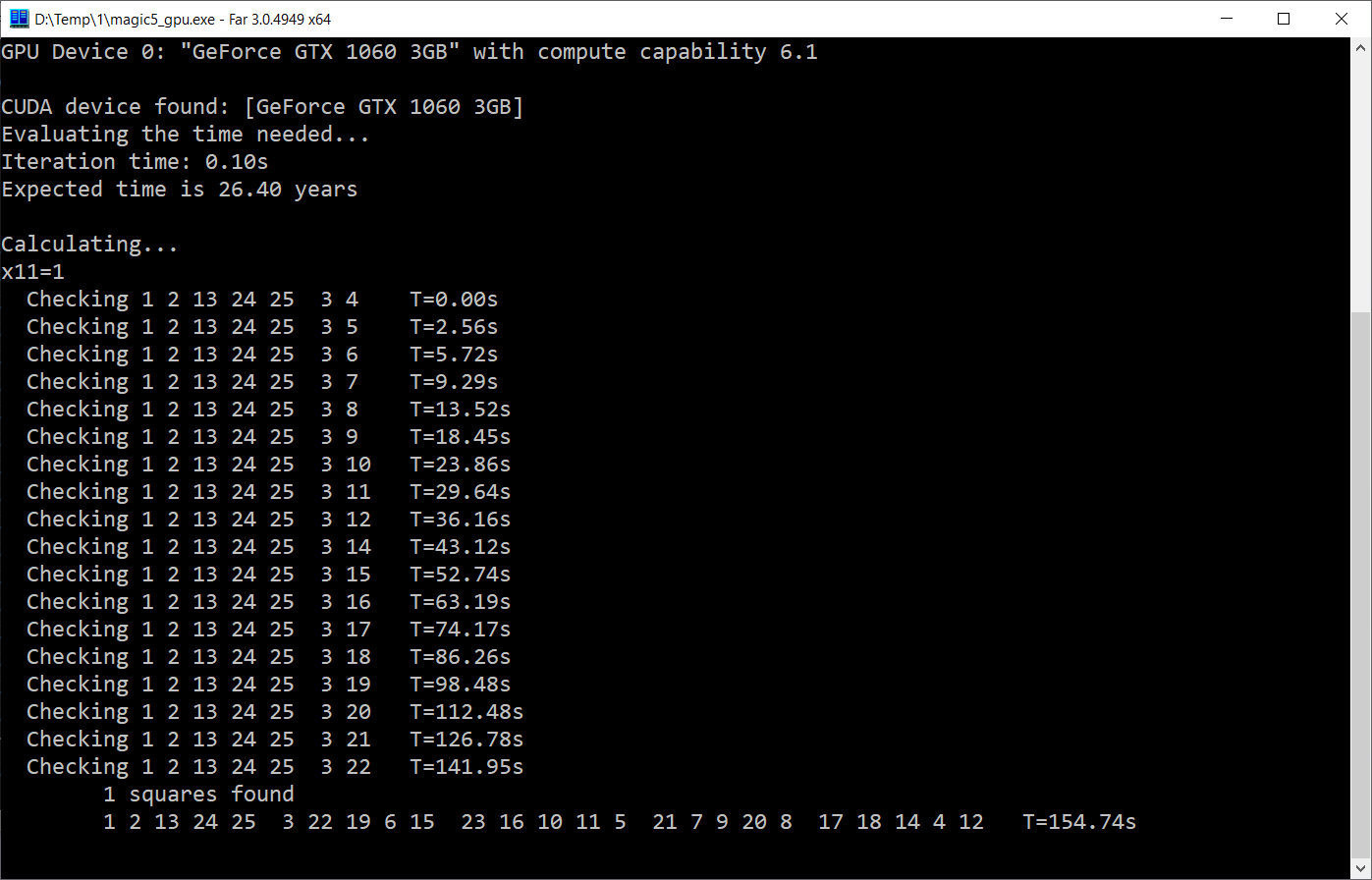
Как можно видеть, GPU-версия выполняется за 0.1с, что в 15 раз быстрее. И я даже наверно доживу до окочания расчета. Конечно, это тоже очень медленно — физических блоков в видеокарте явно больше чем 15, и теоретически можно было бы расчитывать на прирост хотя бы раз в 100. Но либо я не умею «это» готовить, либо такой тип задач не очень ложится на логику работы CUDA.
В принципе, результаты можно было бы и не выкладывать, ибо по большому счету, хвастаться нечем, даже на простой детский вопрос «сколько всего существует магических квадратов 5×5» ответа пока нет. Но с другой стороны, я все же решил все это выложить из нескольких соображений.
— Это интересно и заставляет поломать голову и попробовать что-то новое. Не так уж много можно придумать задач, на решение которой нужно 100 лет.
— В результате получился достаточно интересный и кроссплатформенный бенчмарк, позволяющий сравнить скорость вычислений на разных ПК.
— Данные результаты будут интересны с исторической точки зрения — будет любопытно лет через 10 запустить этот же код на каком-нибудь Core i17 с GeForce 10600 и сравнить результаты. Кстати, если кто может запустить код на старом ПК, сделанном лет 10 назад, тоже было бы интересно.
— Наконец, может кто-то укажет на узкое место в коде или на то, что я сделал не так. Учиться никогда не поздно.
Заключение
Как можно видеть, даже такая простая «школьная» задача с, казалось бы, несложной арифметикой можеть оказаться непростой для вычислений.
Для желающих сделать эксперименты самостоятельно, код и исполняемые файлы выложены в архиве.
Windows-версия — cloud.mail.ru/public/3NJX/3o6c7×6kX
Linux-версия — cloud.mail.ru/public/4csS/2HGCiNurP
Также объявляется конкурс на самый быстрый и самый продолжительный результат :) Особенно интересно было бы посмотреть на новые процессоры i9 с видеокартами GTX2060, ну, а если у кого-то есть доступ к AWS и узлам с профессиональными GPU, было бы совсем круто. Лучшие результаты будут добавлены в текст.
