Математика за оптимизаторами нейронных сетей07.06.2021 19:01

В этой статье мы поговорим о математике градиентного спуска, почему при обучении нейронных сетей применяется стохастический градиентный спуск и о вариации SGD (Stochastic Gradient Descent) с использованием скользящего среднего (SGD с momentum и Nesterov Accelerated Gradient).

mibft6_v8ig1dql4c45iuqvj0sw.png

Градиентный спуск

Предполагается, что вы знакомы с понятием нейронной сети, вы имеете представление, какие задачи можно решать с помощью этого алгоритма машинного обучения и что такое параметры (веса) нейронной сети. Также, важно понимать, что градиент функции —  это направление наискорейшего роста функции, а градиент взятый с минусом это направление наискорейшего убывания. - \nabla_\theta J(\theta) — это антиградиент функционала,
где \theta — параметры функции (веса нейронной сети), J(\theta) — функционал ошибки.

Обучение нейронной сети —  это такой процесс, при котором происходит подбор оптимальных параметров модели, с точки зрения минимизации функционала ошибки. Иными словами, осуществяется поиск параметров функции, на которой достигается минимум функционала ошибки. Происходит это с помощью итеративного метода оптимизации функционала  ---градиентного спуска. Процесс может быть записан следующим образом:

\Delta \theta(t) = - \eta\nabla_\theta J(\theta(t)),

\theta(t + 1) = \theta(t) + \Delta \theta(t) = \theta(t)- \eta\nabla_\theta J(\theta(t)),

где t — это номер шага, \eta — размер шага обучения (learning rate). В результате шага оптимизации веса нейронной сети принимают новые значения.

Виды градиентного спуска


  • Пакетный градиентный спуск (batch gradient descent).

    При этом подходе градиент функционала обычно вычисляется как сумма градиентов, учитывая каждый элемент обучения сразу. Это хорошо работает в случае выпуклых и относительно гладких функционалов, как например в задаче линейной или логистической регрессии, но не так хорошо, когда мы обучаем многослойные нейронные сети. Поверхность, задаваемая функционалом ошибки нейронной сети, зачастую негладкая и имеет множество локальных экстремумов, в которых мы обречены застрять, если двигаться пакетным градиентным спуском. Также обилие обучающих данных, делает задачу поиска градиента по всем примерам затратной по памяти.

  • Стохастический градиентный спуск (stochastic gradient descent)

    Этот подход подразумевает корректировку весов нейронной сети, используя аппроксимацию градиента функционала, вычисленную только на одном случайном обучающем примере из выборки. Метод привносит «шум» в процесс обучения, что позволяет (иногда) избежать локальных экстремумов. Также в этом варианте шаги обучения происходят чаще, и не требуется держать в памяти градиенты всех обучающих примеров. Под SGD часто понимают подразумевают описанный ниже.

  • Mini-batch градиентный спуск

    Гибрид двух подходов SGD и BatchGD, в этом варианте изменение параметров происходит, беря в расчет случайное подмножество примеров обучающей выборки. Благодаря более точной аппроксимации полного градиента, процесс оптимизации имеет большую эффективность, не утрачивая при этом преимущества SGD. Поведение трёх описанных варианта хорошо проиллюстрировано на картинке ниже.

imageИсточник

В общем случае, при работе с нейронными сетями, веса оптимизируют стохастическим градиентным спуском или его вариацией. Поговорим о двух модификациях, использующих скользящее среднее градиентов.

SGD с импульсом и Nesterov Accelerated Gradient

Следующие две модификации SGD призваны помочь в решении проблемы попадания в локальные минимумы при оптимизации невыпуклого функционала.
image
Гладкая выпуклая функция
image
Функция с множеством локальных минимумов (источник)

Первая модификация

При SGD с импульсом (или SGD with momentum) на каждой новой итерации оптимизации используется скользящее среднее градиента. Движение в направлении среднего прошлых градиентов добавляет в алгоритм оптимизации эффект импульса, что позволяет скорректировать направление очередного шага, относительно исторически доминирующего направления. Для этих целей достаточно использовать приближенное скользящее среднее и не хранить все предыдущие значения градиентов, для вычисления «честного среднего».
Запишем формулы, задающие этот подход:

v(t) = \alpha v(t-1) + \eta \nabla_\theta J(\theta(t)),

\theta(t+1) = \theta(t) - v(t),

v(t) — это накопленное среднее градиентов на шаге t, коэфициент \alpha \in [0,1] требуется для сохранения истории значений среднего (обычно выбирается близким к 0.9.

Вторая модификация

Nesterov accelerated gradient отличается от метода с импульсом, его особенностью является вычисление градиента при обновлении v(t) в отличной точке. Эта точка берётся впереди по направлению движения накопленного градиента:


v(t) = \alpha v(t-1) + \eta \nabla_\theta J( \theta(t) - \alpha v(t-1)),

\theta(t+1) = \theta(t) - v(t).

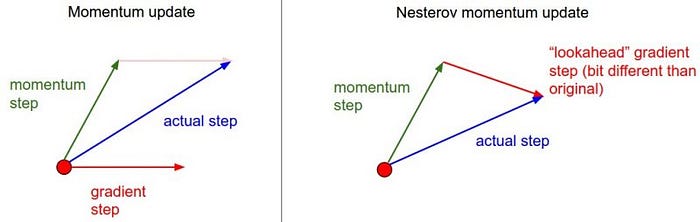
На картинке изображены различия этих двух методов.

image
источник

Красным вектором на первой части изображено направление градиента в текущей точке пространства параметров, такой градиент используется в стандартном SGD. На второй части красный вектор задает градиент сдвинутый на накопленное среднее. Зелеными векторами на обеих частях выделены импульсы, накопленные градиенты.

Заключение

В этой статье мы детально рассмотрели начала градиентного спуска с точки зрения оптимизации нейронных сетей. Поговорили о трёх разновидностях спуска с точки зрения используемых данных, и о двух модификациях SGD, использующих импульс, для достижения лучшего качества оптимизации невыпуклых и негладких функционалов ошибки. Дальнейшее изучение темы предполагает разбор адаптивных к частоте встречающихся признаков подходов таких как Adagrad, RMSProp, ADAM.

Данная статья была написана в преддверии старта курса «Математика для Data Science» от OTUS.

Приглашаю всех желающих записаться на demo day курса, в рамках которого вы сможете подробно узнать о курсе и процессе обучения, а также познакомиться с экспертами OTUS

— ЗАПИСАТЬСЯ НА DEMO DAY

© Habrahabr.ru