Математика для 3D-приложений. Урок 114.06.2022 17:01

Введение: зачем нужна линейная алгебра в 3D и операции над векторами.

fb5577142b91193652bef8756c24f2b4.png

Это первый, вводный урок по линейной алгебре для разработки 3D-приложений от Александра Паничева — ведущего разработчика логики в UNIGINE. В этом уроке разберемся зачем 3D-разработчикам вообще нужна линейная алгебра, а также рассмотрим основные операции над векторами.

Во втором уроке будут разобраны более сложные темы: углы Эйлера, кватернионы и матрицы.

Почему именно линейная алгебра?

Во-первых, в любом 3D-приложении мы так или иначе сталкиваемся с векторами и вращениями. Vector, Matrix — об этих терминах слышали все. Мы двигаем объекты, поворачиваем их на определенные градусы, вытаскиваем в процессе всякую полезную информацию для дальнейших вычислений… Поэтому умение оперировать с ними быстро и эффективно, минуя лишнюю тригонометрию там, где она не нужна, крайне важно!

Во-вторых, даже после работы в геодезических координатах все сводится к обычному трехмерному евклидову пространству. Таков уж рендер: простой, не кривой. Поэтому знать линал — основа жизни 3D-шника!

А кроме того, у многих знания по математике обрывочные. Надо заполнить пробелы!

Из чего состоит математическая библиотека 3D-движка?

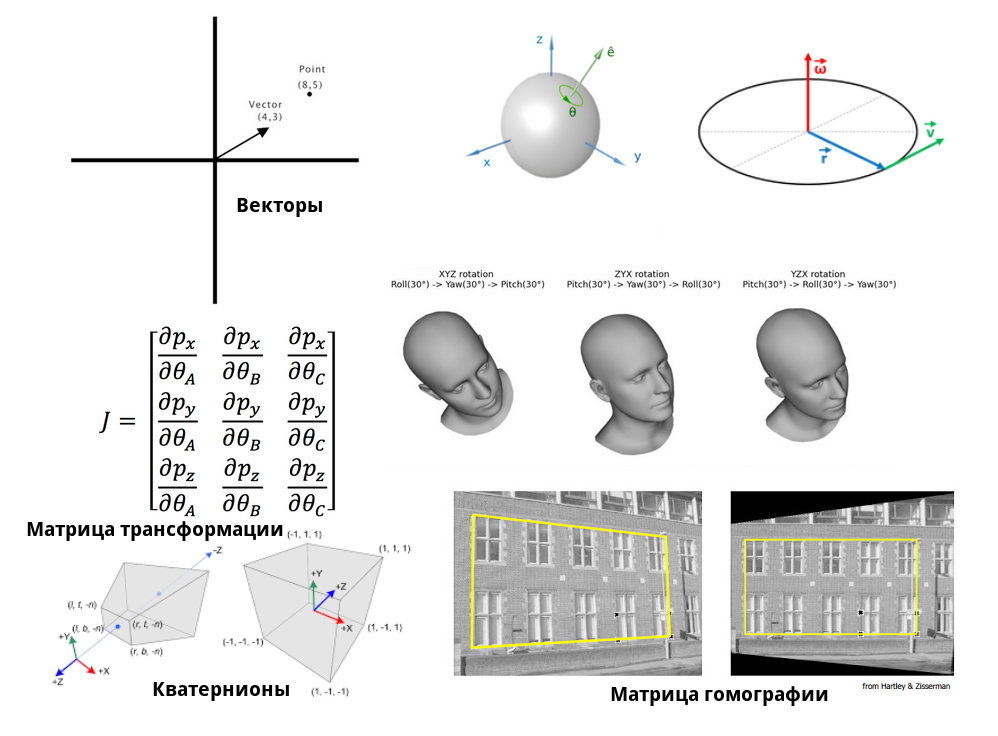
0a4018272ad713a6ac8ece3b392f30d5.png

В игровых движках обычно есть 3 группы:

  1. Вектора. Может быть точкой, радиус-вектором, направлением (нормаль), линейной скоростью, угловой скоростью, углами в градусах или радианах (углах Эйлера).

Вектор-точка — просто позиция в пространстве. Радиус-вектор означает, что его начало находится в 0 относительно начала координат. Направление — это нормализованный вектор, который можно назвать радиус-вектором фиксированной (единичной) длины. Линейная скорость и угловая скорость отвечают за динамику. А углы Эйлера подробно разберем во втором уроке.

  1. Матрицы. Матрица смещения, матрица вращения, матрица масштабирования, матрица трансформации (TRS), проекции (перспективная, ортографическая), система линейных алгебраических уравнений, матрица Якоби и Тензор инерции, матрица гомографии.

Матрица гомографии используется в камерах для правильной проекции с разных углов обзора.

  1. Кватернионы. Вращение, выраженное в кватернионах.

Через что можно представить ориентацию объекта?

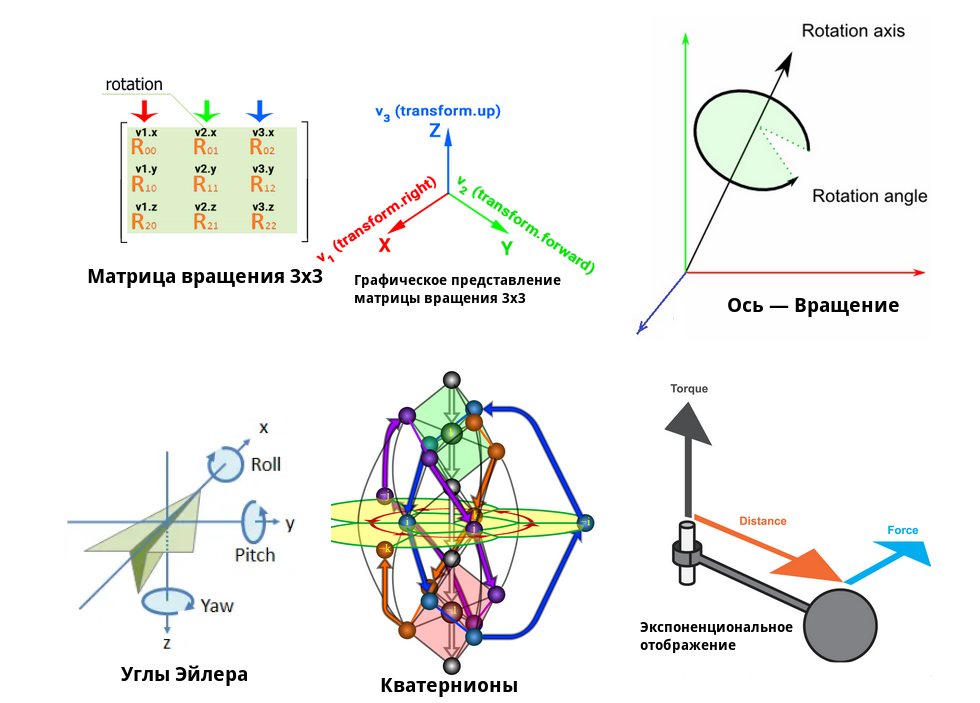
3c8b5ce36130a3415237790bbb6cf819.png

  1. Матрица вращения 3×3 (Matrix 3×3). Чтобы получить поворот, достаточно перемножить матрицу вращения на вектор или на матрицу трансформации. Но возникают проблемы, когда нужно плавно вращать объект из одних углов в другие — простыми способами это не сделать. Кроме того, легко накапливаются ошибки округлений, если много раз перемножать матрицу. В результате объект становится скошенным (ромбообразным).

  1. Углы Эйлера (Euler Angles). Состоят из крена (Roll), тангажа (Pitch) и рысканья (Yaw). С этим легко разобраться и легко представить. Интерполяция вокруг одной оси тоже делается легко, но интерполяция по двум осям будет происходить не по кратчайшему пути, а по S-образной кривой. Кроме того, удобно ограничивать вращение сочленений в градусах. Главный недостаток — шарнирный замок (о нем позже).

  1. Ось-Вращение (Axis — Angle). Простой метод с простой интерполяцией и удобным ограничением вращения. Однако с помощью него неудобно складывать несколько вращений вместе, чтобы получить единый объект вращения.

  1. Кватернионы (Quaternion). Можно представить, как точку на поверхности трисферы единичного радиуса в четырехмерном пространстве. Легко складываются вращения, интерполяция идет по кратчайшему пути. Нет такого недостатка, как шарнирный замок. Просто ограничивать вращение. Однако сложны для прочтения. Кроме того, накапливают ошибку при многоразовом перемножении — нужно периодически нормализовать.

  1. Экспоненциальное отображение (Exponential Map). Напоминает Ось-Вращение. Легко складывать вращения. Меньше степеней свободы, поэтому годится только как динамика вращения.

  1. 6-мерное представление (6D Representation). Зачастую случайно получается в конце вычислений. Часто используется в нейросетях. По сути — две оси: Forward и Up. Используется как основа для создания матрицы 3×3.

Кстати…

bddccc024884629d83336379171b21dd.png

Для x нужно взять cos от угла, а для y — sin от угла. Также можно использовать функцию atan2, которая работает в диапазоне от -π до π.

Пару слов про производительность мат. функций

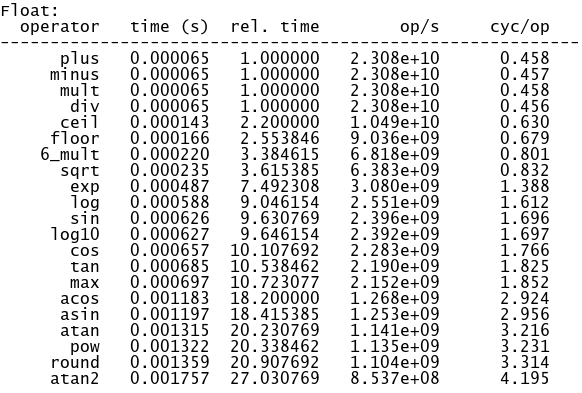
05e86a21b3684f15935d899fa039927e.png

Сложение (plus), вычитание (minus), умножение (mult) и деление (div) занимает примерно одно время. А, например, вычисление квадратного корня (sqrt) в 3,6 медленнее. Самое медленное: аркосинусы (acos), арксинусы (asin), арктангенсы (atan) и округление (round).

Выводы:

  1. Тригонометрия очень медленная. Особенно та, что возвращает углы.

  2. Взятие квадратного корня (sqrt) по скорости примерно как 6 умножений (6_mult).

  3. Вычисление наибольшего элемента (max) и округление (round), внезапно, сильно медленные.

Операции над векторами в 2D

b9e62a36f2cc2d88fa0f30afbc9bce56.png

Основные: сложение векторов, вычитание векторов, умножение вектора на скаляр и нормализация вектора. У них внутри простой код с простой нормализацией и взятием длины.

Пример. Есть персонаж, он стоит в начале координат и хочет добежать до дерева. В этом примере можно использовать все 4 базовые операции:

f7e4d6051116881764d035279af76f96.png

vec2 pos = vec2(2,2); // позиция персонажа
vec2 tree = vec2(6,4); // позиция дерева
vec2 distance = tree - pos // radius vector
vec2 direction = distance.normalize(); // нормализованный unit vector

vec2 new_pos = pos + direction * IFps // берем старую позицию и умножаем вектор на скаляр

dot product — скалярное произведение векторов

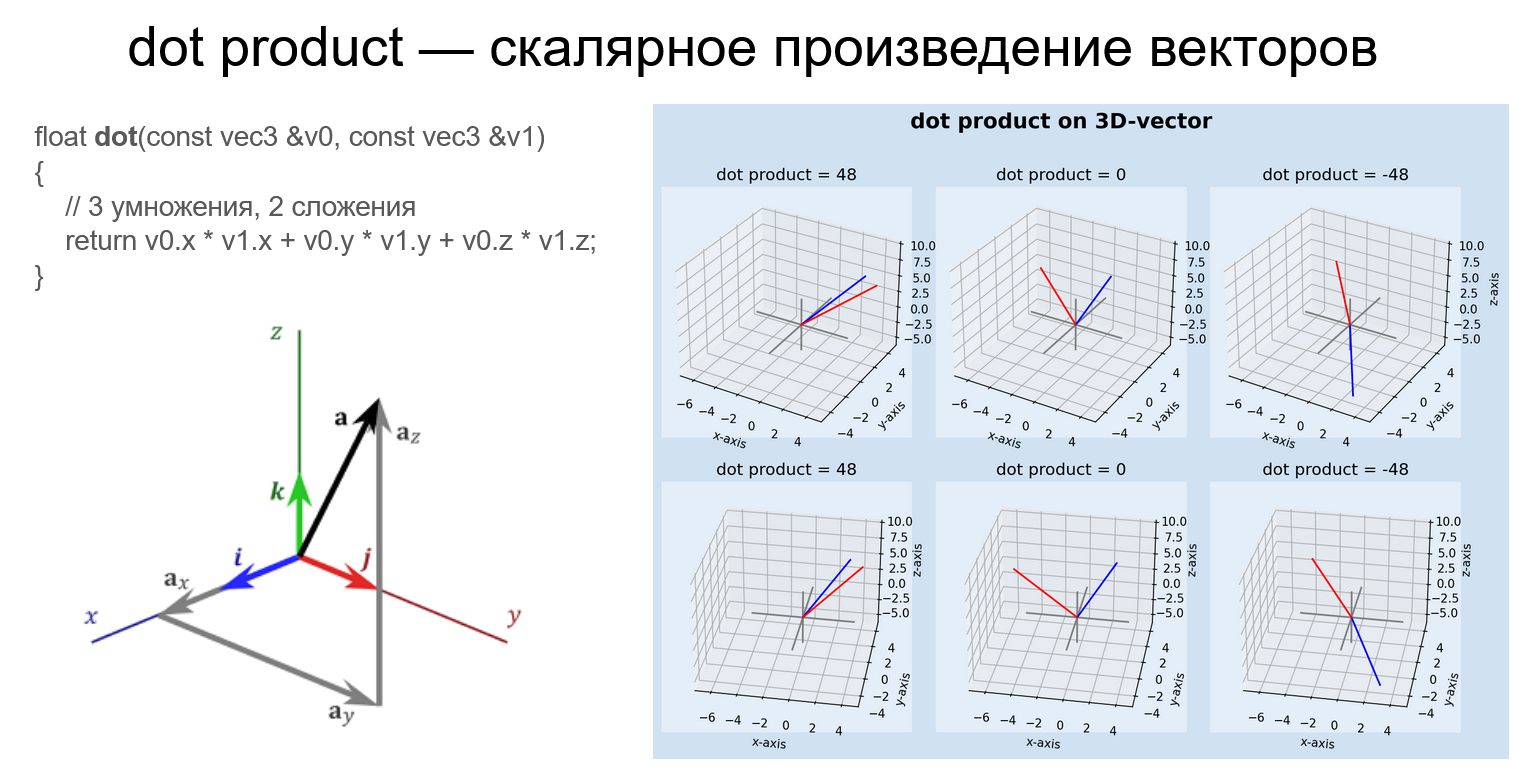
Это операция над двумя векторами, результатом которой является скаляр: 

float dot(vec2 v0, vec2 v1) { v0.x * v1.x + v0.y * v1.y; // 2 умножения, 1 сложение }

d10a5c04076efa615d7771562968abae.png

  1. Равен произведению длин векторов на косинус угла между ними: 

dot(a,b) = |a||b|cos(angle_rad)

  1. Скалярное произведение > 0, если вектора направлены в одну сторону, 0 — если вектора перпендикулярны и < 0, если направлены противоположно.

  2. Является длиной проекции произвольного вектора на нормализованный вектор:

proj_length = dot (a, normal)

  1. Скалярное произведение самого на себя является квадратом длины вектора: 

dot(a,a) == length2(a)

  1. Получить вектор-проекцию можно так: 

proj_point = b*dot(a,b)/dot(b,b)

  1. dot(a,b) == dot(b,a)

Где еще используется dot?

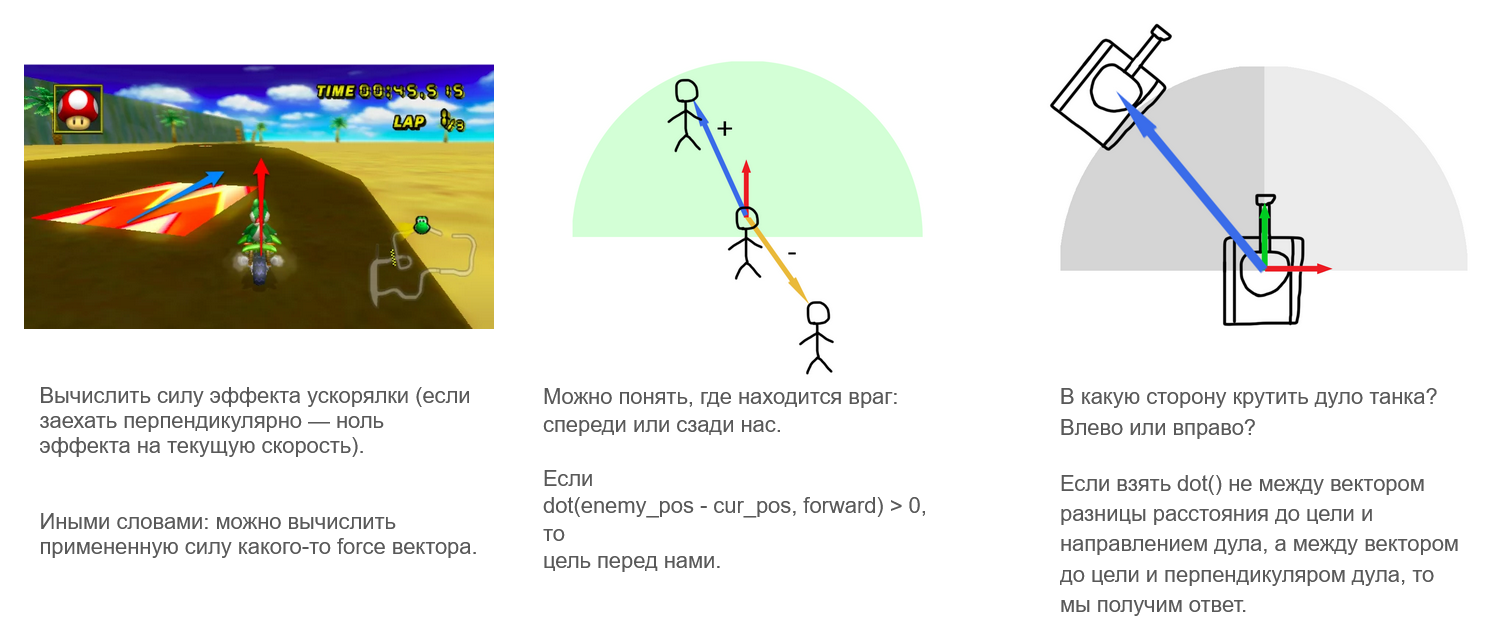
125db1aa7fa7d5136157d6f727c08029.png

А как найти перпендикуляр?

В 2D все просто: переставляем (x, y) местами и у какого-нибудь компонента меняем знак. Например, для поворота по часовой стрелке нужно поставить минус у второго компонента, а против часовой — у первого.

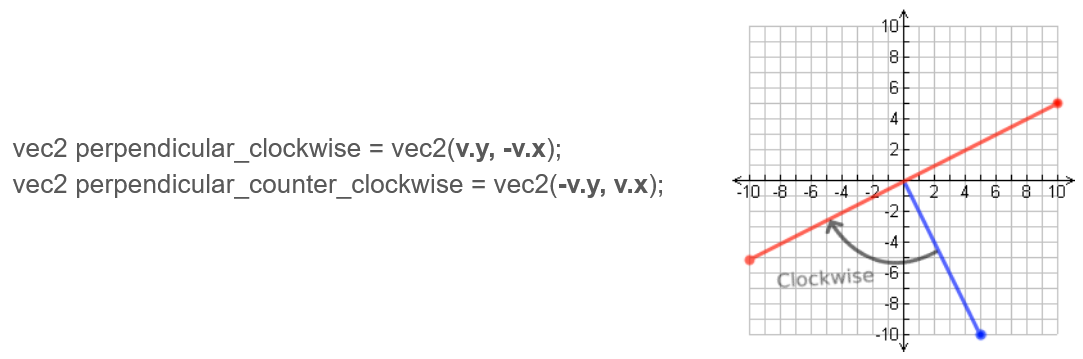
ba32d34aabb7220ad0602e59e9ea2927.png

А если совместить dot и нахождение перпендикуляра?

Для этого есть операция skew product — косое произведение векторов. Это операция над двумя векторами, результатом которой является псевдоскаляр: 

float skew(vec2 v0, vec2 v1) { v0.x * v1.y - v0.y * v1.x; // 2 умножения, 1 вычитание }

e9f64548fc4a3fb7a49a712bc7f80773.png

В UNIGINE такая операция называется cross.

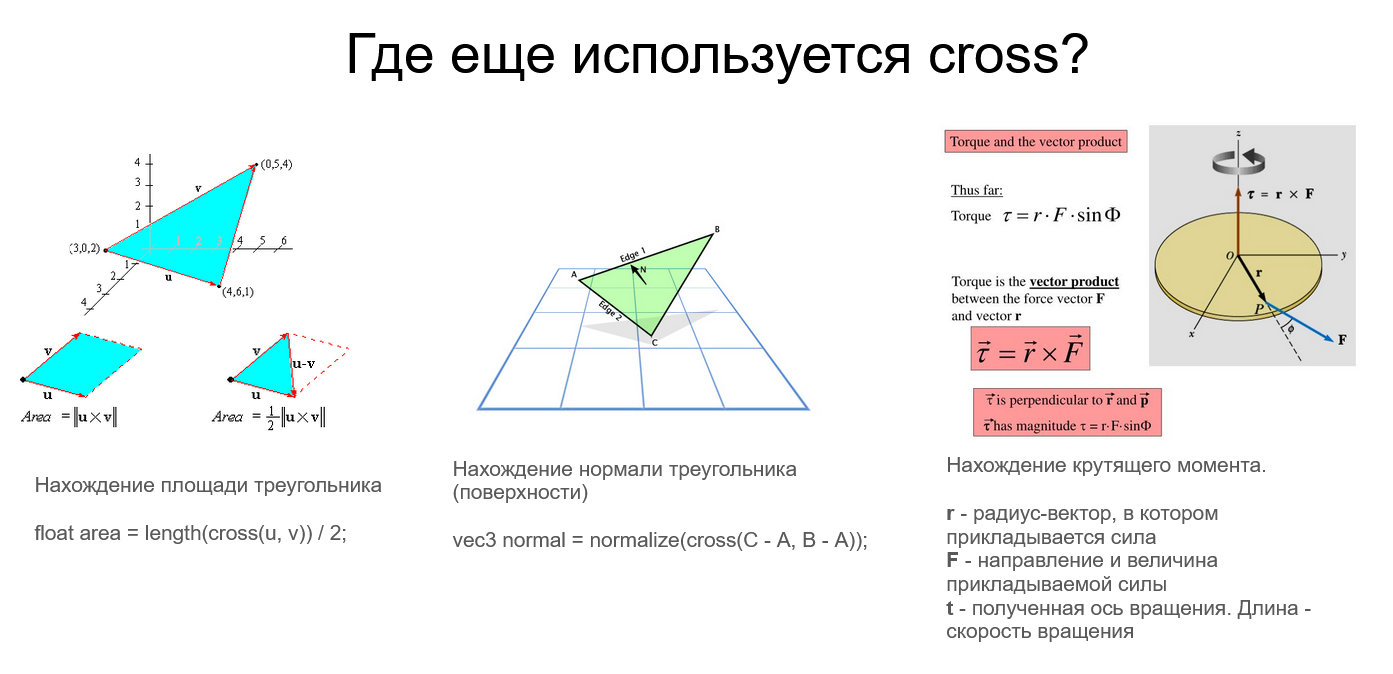
Где еще используется skew?

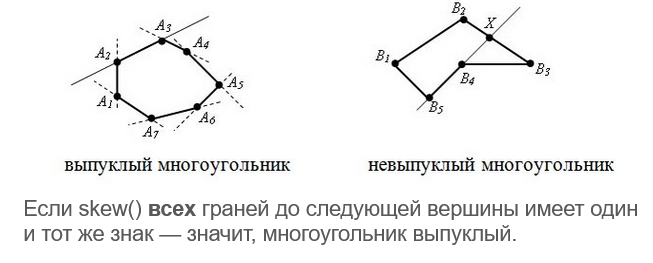
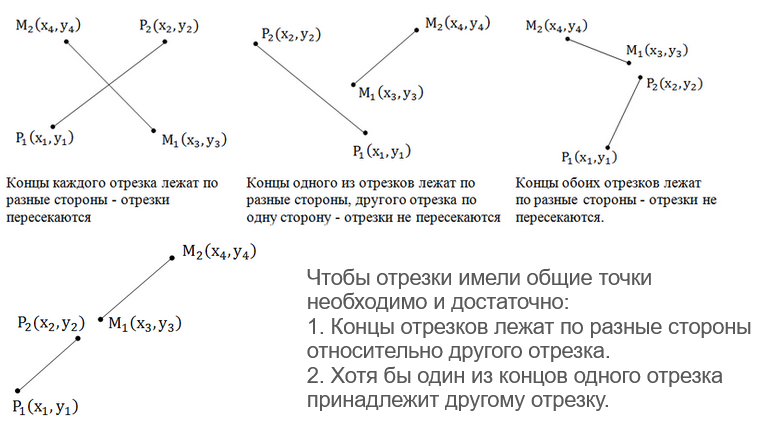
5e712c05b4f9c8d7daf26c7fd6385956.png4a04bafad78d61a5fc5af8520fd3078e.png6bbcab8eaa20f6a93869c33451437483.pngcc0586f0150b31dfbcfc47a8204db0c6.png8f12426128f2006dec860267db3095f6.png

Операции над векторами в 3D

Работа с векторами в 3D мало чем отличается от 2D. Можно сказать, что решив задачу в 2D, вы решите ее и в 3D. Так, например, скалярное произведение векторов dot product, о котором речь ниже, одинаково работает в 2D и 3D.

Но в 3D появляется операция cross product — векторное произведение векторов. О нем поговорим в конце главы.

897f777422879ac0becdfc2af9e428ea.png0498a567b58b91d63ee87a54eb9b653a.png

Где еще используется dot в 3D?

В шейдерах. Повсеместно. Например, рассмотрим простейшую модель освещения Ламберта (Lambert, Lambertian Reflectance, или Diffuse Light):

У нас есть модель с набором нормалей и где-то источник света.

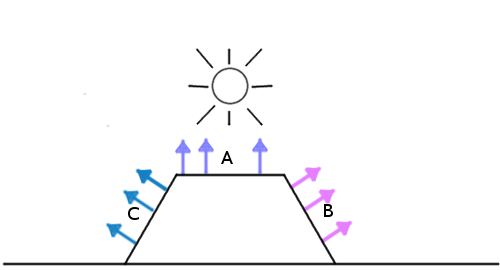
948814545d70c86098f92de01a063934.png

Просто вычисляем угол между источником света и нормалью поверхности. Чем меньше угол, тем ярче пиксель.

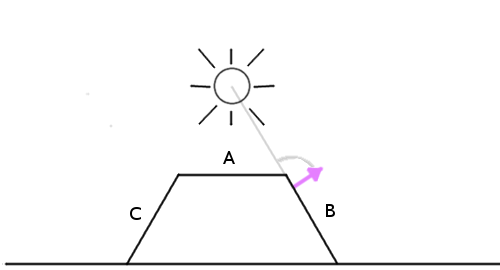
c140cfe74c471127915c5677fb4dbb3e.png

Вот как выглядит алгоритм:

  1. Получаем вектор нормали текущего пикселя — NormalVector.

  2. Получаем вектор направления света относительно текущего пикселя — LightVector.

  3. Нормализуем векторы.

  4. Вычисляем угол между ними — dot.

  5. Умножаем конечный цвет на этот коэффициент и коэффициент затухания.

float diffuse = max(dot( LightVector, NormalVector ), 0.0);
float attenuation = saturate(1.0 - DistanceToLight / LightRadius);

FragColor = color * diffuse * attenuation;

4dbbfe07f32abc79777d87265a83e595.png

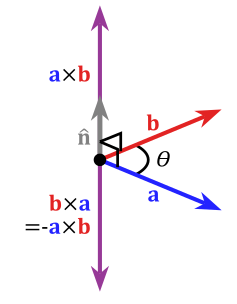
cross product — векторное произведение векторов

cross product появляется в 3D-пространстве. Это операция над двумя векторами, результатом которой является вектор, перпендикулярный исходным двум: 

vec3 cross(const vec3 &v0, const vec3 &v1)
{
    vec3 ret;
    ret.x = v0.y * v1.z - v0.z * v1.y;
    ret.y = v0.z * v1.x - v0.x * v1.z;
    ret.z = v0.x * v1.y - v0.y * v1.x;
    return ret; // 6 умножений, 3 вычитания
}

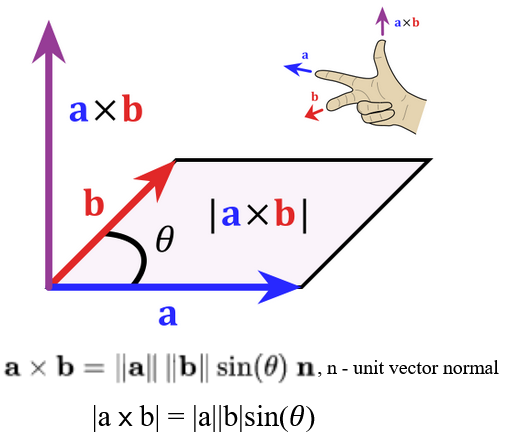
4a0bf892adbab3a9709bf5c8a8286e5a.png

  1. Длина результирующего вектора равна площади параллелограмма, образованного исходными векторами.

  2. Длина результата — это еще и |a||b|sin(angle_rad)

  3. Перпендикуляр строится по правилу «правой руки».

  4. Не коммутативен. То есть: cross(a,b) != cross(b,a)

ed2f5fb074b20d914d93d92293c166c6.pnge878ccead8ae0a0a593c3202fb5bcda7.png

Если вам вдруг интересно как потом этот результат можно использовать для вращения тела: 

vec3 torque; // крутящий момент
quat rotation; // текущее вращение тела

// qnew = q0 + 0.5 * w * q0
quat q = (rotation + quat(torque * ifps) * rotation * 0.5f).normalize();

7343159071713d78ab2b3a1834a5b158.png

Конечно, задачу с танком можно решить и через: 

vec3 rel_pos =
    inverse(tank_transform_mat4) * vec3_target_position;

Если известна обратная матрица, то такой способ будет примерно равен по скорости комбинации dot (cross).

Но… Не всегда у нас есть обратная матрица на руках. Мы можем быть в процессе изменения направления. Да и не всегда есть матрица как таковая.

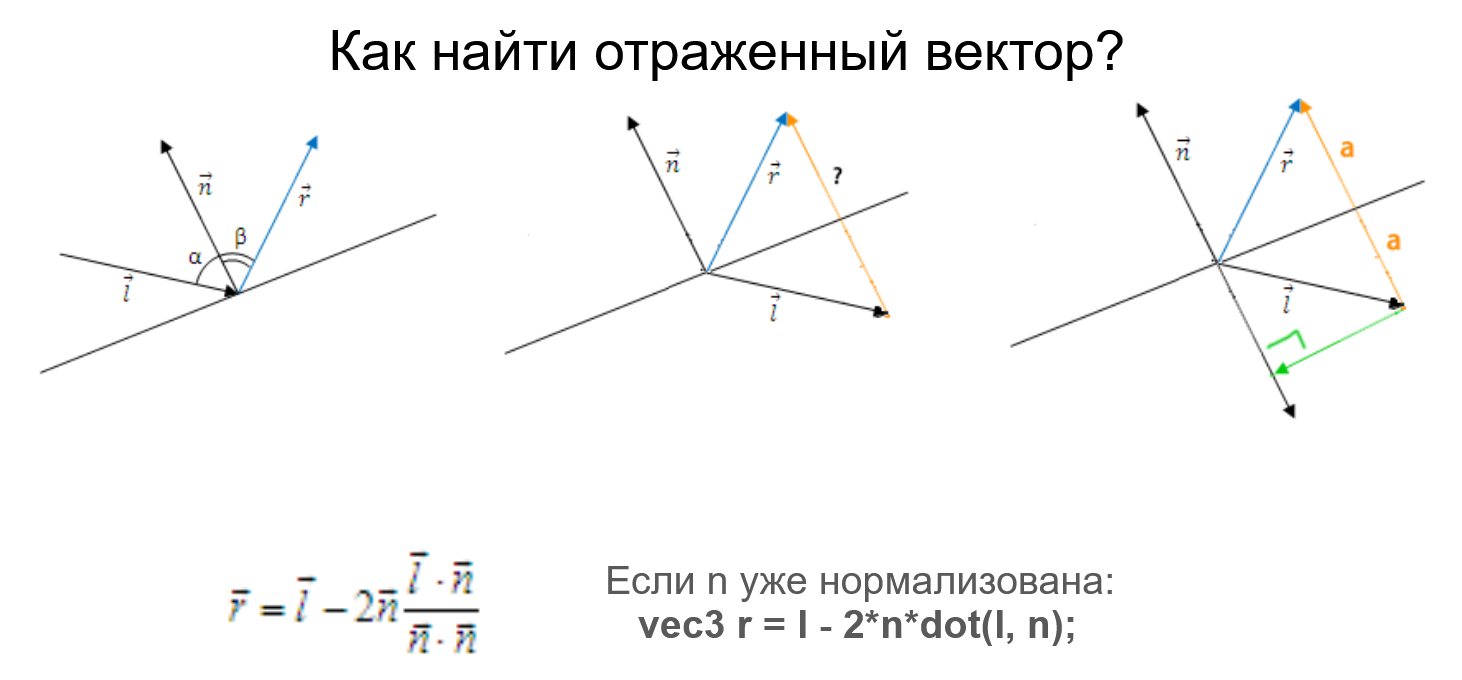
Fun fact: Помните задачу нахождения отраженного вектора? Зная ее, можно легко то же самое сделать через dot (еще и быстрее будет работать!): 

vec3 new_dir = dir - normal * dir(dir, normal);

dot (cross ()) — scalar triple product, смешанное произведение

Скалярное произведение вектора a на векторное произведение векторов b и c

float scalar_triple(const vec3 &a, const vec3 &b, const vec3 &c)
{
    // 9 умножений, 5 сложений
    return dot(a, cross(b, c));
}

cc436fc6e2946710f11f16859c1fbf41.png

  1. Модуль смешанного произведения численно равен объему параллелепипеда, образованного векторами a, b, c.

  2. dot(a,cross(b,c)) == dot(cross(a,b),c)

  3. Равен детерминанту (определителю) матрицы, составленной из векторов a, b, c. В том числе и по перфу.

  4. Аналог skew в мире 3D.

* * *

На этом пока все. Во втором уроке разберем сложные темы: углы Эйлера, кватернионы и матрицы.

© Habrahabr.ru