Математические основы кодирования и шифрования11.08.2020 15:02

Информационное взаимодействие абонентов в компьютерных и связных сетях подвергается возмущениям, которые приводят к возникновению ошибок и возмущений разного рода. Помимо возникновения ошибок в передаваемых сообщениях возможен несанкционированный доступ к содержанию сообщений нарушителя. Борьба с этими нежелательными явлениями ведется тысячелетиями, но с переменным успехом. Создатели Интернета задумывали его совсем не таким, каким он стал сейчас. О хакерах тогда и не думали.

Основные теоретические проблемы информационного противостояния, задачи по их решению возлагаются на теории кодологии, криптологии и стеганологии, в которых во всем мире интенсивно развиваются направления кодоанализа, криптоанализа и стегоанализа. Практические аспекты также не остаются в стороне, но замечу, что в РФ активность не очень-то высока, сказывается инертность молодых (сам я разменял уже 9-й десяток, но администрация Хабра ограничила возрастной ценз 1950 г). Мое мнение, конечно, ограничено наблюдением потомства (вплоть до правнуков) и общением в интернете, а также с обучаемыми и сотрудниками фирмы, где подрабатываю. СМИ тоже добавляют негатива. Кто из молодежи чуть поумнел, уходят за бугор. Поведение остальных видите сами.

Экскурс по публикациям

Разработка (синтез) технических устройств требует от разработчика определенных знаний, умений ими пользоваться и других навыков подобного рода. Существенная составляющая таких знаний — математическая. Это, как правило, алгебра, дискретная математика, геометрия, физика, математическая логика и др. Здесь в статье будем рассматривать алгебраические структуры не совсем в классическом изложении, но с достаточными уровнем строгости и точностью. Главной моей задачей является обеспечение доступности и понятности изложения вещей, которые я использую в своих текстах и изысканиях.

Например, здесь используется поле расширения GF (28) и, если обойтись без него, ничего стоящего изложить не удается. Мои критерии оценки просты. Каждый семестр 2, а то и 3 экзамена и зачеты в разных учебных группах. Там слышу и вижу, что я излагал, выносил на практику, и что мне возвращают в ответах по экзаменационным билетам. Очень полезен анализ экзаменационных ответов, вижу, что следовало бы излагать кое-что по-другому, лучше.

А здесь свойства ZN конечного числового кольца вычетов по составному модулю N =pq используются для поиска решения задачи факторизации больших чисел в рамках нового оригинального подхода. Понятно, что в каждой из последующих публикаций переносить часть стандартных математических средств было бы неразумно, посему принято решение собрать все в одном месте и при необходимости адресовать сюда читателей.

Здесь же рассматривается и используется группа точек эллиптической кривой на плоскости. Операция суммирования в группе очень специального вида, вызывающая недоуменные вопросы, типа как это Вам удается складывать точки кривой, даже от членов ГЭК.

Группы

Предварительно введем ряд необходимых определений.

Определение. Конечное множество А-набор, совокупность любых n объектов ${a_1,a_2,..., a_n}$ , перечисляемых в любом порядке, но среди которых нет повторяющихся. Множества бывают структурированные, над элементами которых задана одна (или более) операция и отношений и неструктурированные, когда операции не заданы.

Ниже, как напоминание, приводится таблица действий (операций) с конечными дискретными множествами, а на диаграммах для наглядности показаны и непрерывные множества А и В.

Таблица операций с множествами

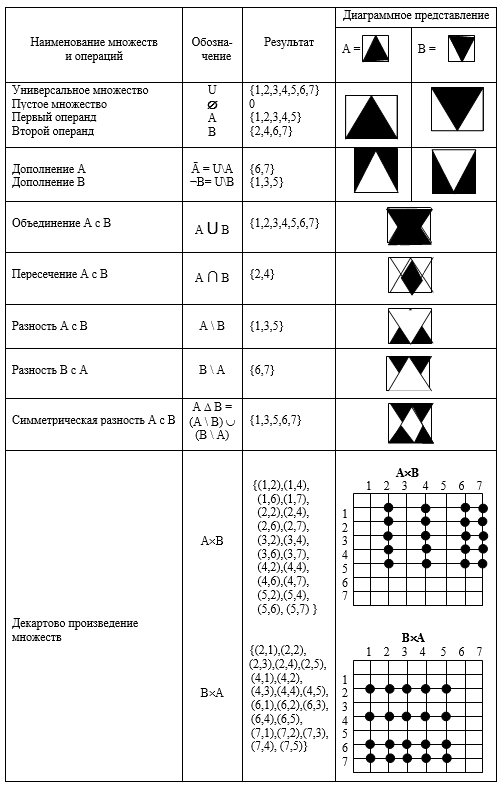
Определение. Операцией называется отображение А×А→А или, например, а·b=с; a, b, c ∊ A. Операции в алгебраических структурах другие нежели в арифметике, рассматриваются: унарные (например, обращение b-1), бинарные, тернарные, …, n-арные (по числу мест для операндов), или умножение перестановок, модулярные (взятие результата по (mod R)) и др. Говорят, что элементы, а и b перестановочны или коммутируют, если ab = ba.

Определение. Группа — это множество G элементов (любой природы), над которыми задана единственная операция, но она может быть сложением (+) и группа называется аддитивной, ее нейтральный элемент (0) или умножением (◦) — называется мультипликативной, ее нейтральный элемент (1), но как правило, операции эти не обычные арифметические, а специальные. Обозначается группа часто символом (G, ◦), среди всех групп важное место отводится симметрическим группам $S_n$ перестановок степени n. Части элементов группы, сохраняющие свойства группы называются подгруппами. В сущности это такие же группы, только меньше исходной. Это неформальное определение группы, формальное будет приведено чуть позже.

Группа G, удовлетворяющая коммутативному закону ba =ab для всех a, b ∊ G называется в честь математика Абеля (1802 -1829) абелевой.

Примером аддитивной группы является набор слов кода Хемминга (см.здесь). Операция в этой группе 16 порядка — суммирование слов по (mod2). С этой группой выполнялась операция разложения в смежные классы группы из 128 слов по подгруппе кода, а также строилась таблица Кели, элементы группы используются в кодере (базис пространства размерности 4) и декодере. Одним словом этот пример наглядно демонстрирует как может использоваться даже маленькая группа для решения очень важной практической задачи (связь).

Очень важными в теории групп являются симметрические группы подстановок (перестановок). Эта важность определяется теоремой, в которой говорится, что для любой группы, возникающей в произвольной предметной области, существует изоморфная ей симметрическая группа (подгруппа) на перестановках. Тогда исследователю новой открытой группы задача ее изучения упрощается. Почти все свойства изоморфной группы перестановок имеют место и в новой группе.

Начнем с простого примера. Заданы n элементов (обозначим их цифрами 1,2,3,…, n) и образуем из них перестановки, число которых n! = 1·2·3·…·n. Ограничимся значением n=3, тогда 3! = 6.

Определение. Порядок группы — число элементов в группе называется ее порядком. В примере число 6 — это порядок группы.

В группе каждый элемент также имеет порядок, который является делителем порядка группы.
Определение. Порядок элемента группы — это наименьший показатель степени элемента в мультипликативной группе (кратности в аддитивной b+b+b+b+…b =nb = 0, порядок =n), при котором он обращается в нейтральный элемент, например ( $р_4$ )3=1, порядок ord ( $р_4$ ) = 3.

В симметрической группе $S_n$ операцией является умножение перестановок. Это умножение аналогично матричному умножению, так как каждой перестановке степени n ставится в соответствие квадратная перестановочная матрица размерности n×n, в которой каждая строка и столбец содержат единственную единицу. Ниже это показано для симметрической группы $S_3$ .

Для удобства работы с группой и ее элементами математиком Кели предложена таблица операций группы (ограниченного размера). В клетке на пересечении строки и столбца ставится результат операции с элементами, которые их обозначают. Результат (как и обозначение строк/столбцов) в таблице представляется десятичными номерами элементов, что экономит место.

Таблица умножения элементов (перестановок) группы $S_3$

Заполнение 36 клеток таблицы умножения упрощается, если воспользоваться свойствами таблицы Кели.
— Все строки и столбцы содержат элементы всей группы.
— Крайние столбцы лексикографически упорядочены и встречно направлены (1-й сверху/вниз — последний наоборот)
— На главной диагонали таблицы стоят квадраты элементов, если там стоит 1, то элемент ей соответствующий — инволюция; инволюциями в $S_3$ являются $р_1,р_2,р_3,р_6$
— Относительно диагоналей матрицы выполняется симметрия положений элементов.
Свойства таблицы позволяют при ее заполнении ограничиться вычислениями только 13 пар элементов (выше они показаны).

Симметрическая группа

Группа $S_3$ имеет маленький порядок (6) и для иллюстрации свойств не очень удобна. Далее будут приводится примеры с симметрической группой $S_4$ 24 порядка. Все четные перестановки степени n образуют знакопеременную подгруппу в симметрической группе, обозначаемую символом Аn.

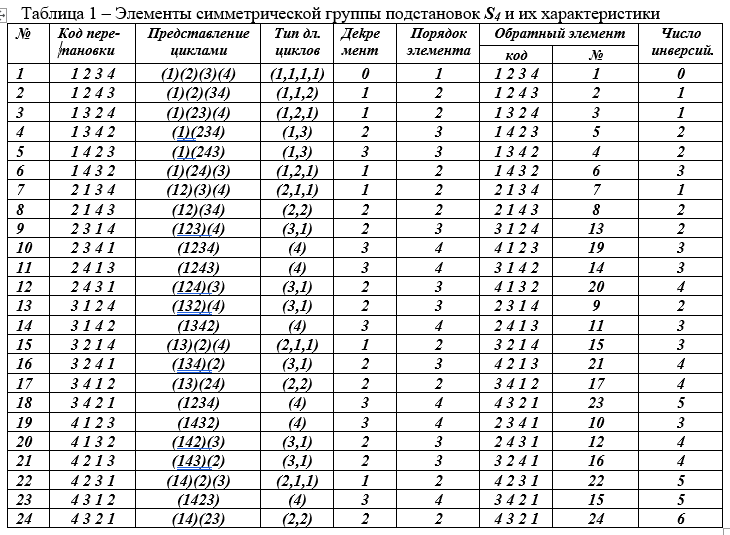
Таблица 2 может использоваться для нахождения произведений любой пары элементов $S_4$ или для их целой цепочки, но находятся последовательным умножением результата на следующий элемент. Переставлять местами элементы в произведении нельзя. Операция умножения перестановок не коммутативна, как и умножение матриц. Один элемент при многократном умножении на себя, пока не получится 1, образует циклическую группу из всех промежуточных результатов. Порядок такой циклической подгруппы является порядком порождающего элемента, он должен делить порядок исходной большой группы.

По таблице умножения находятся подгруппы в составе большой группы. Необходимо помнить, что порядок меньшей подгруппы должен делить порядок большей.
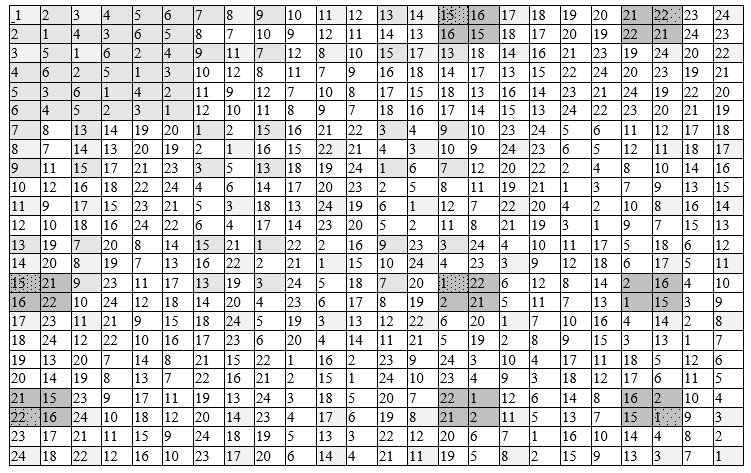
Построим циклическую группу с порождающим р14 элементом. Входим в таблицу 2. В строке 14 находим на пересечении с р14 столбцом элемент р24; в строке 24 находим в клетке пересечения с 14 столбцом элемент р11 и наконец в клетке строки 11 на пересечении со столбцом 14 находим элемент р1, т.е. нейтральный элемент 1. Итак, р14·р14·р14·р14 = р1, это элементы подгруппы 4-го порядка, значение которого нацело делит порядок 24:4 = 6. Для нее можно построить таблицу Кели и в ней не будут появляться никакие элементы кроме найденных.В этой подгруппе элементы р14 и р11 имеют 4-й порядок, а р24 второй — это инволюция.

Морфизмы групп

Отображение f группы (G,*) в группу (G', ◦) называется гомоморфным (или гомоморфизмом), если для любых а, b ∊ G, f (a*b) = f (a)◦f (b). Обычно продолжают эти равенства так f (е) = е',
f (a-1) = (f (a)) -1. Запись справа от равенства обозначает образ и называется образом, слева — прообразом отображения f. Операции над образом и прообразом в общем случае не совпадают. Прообраз единицы (G', ◦) при гомоморфизме f называется ядром этого гомоморфизма и обозначается ker f. Хорошо известным со школьных лет примером является такое отображение log (a◦b) = log (a) + log (b).

Элементы образа с операцией над ними (+), а в прообразе элементы связаны операцией (◦) умножения. Гомоморфный образ группы есть группа (подгруппа), т.е., если f-гомоморфизм G на G' и G — группа, то и G' — группа. Гомоморфизм — обобщение изоморфизма групп: если f — взаимно однозначное гомоморфное отображение G на G', то оно изоморфно, что обозначается так G≈G'.
Две группы G и G' с операциями (·) и (*) называются изоморфными, если существует отображение f: G → G' такое, что (отображение f сохраняет групповую операцию) образа;

Теорема. Пусть Н — нормальная подгруппа группы G и G=G/H. Тогда отображение f группы G на G, заданное формулой f (a) =a является гомоморфизмом. Ядро этого гомоморфизма есть Н. Этот гомоморфизм часто называют естественным (каноническим).
Гомоморфизмы группы по существу исчерпываются каноническими гомоморфизмами.

Выполним разложение группы G 24-го порядка по ее подгруппе H ={1,8, 17,24} в смежные классы и построим для этого разложения факторгруппу по подгруппе Н. С этой целью выпишем в столбцы левые и правые произведения элементов подгруппы Н.

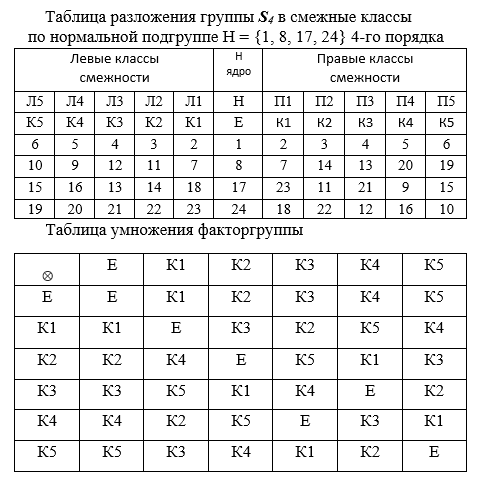
В таблице разложения группы G порядка 24 на классы смежности по подгруппе Н обозначены столбцы л1, л2, л3, л4, л5 имена левых и п1, п2, п3, п4, п5 — правых смежных классов, ведущие представители классов по одному на столбец выписаны в следующей строке.

Средний столбец Н — группа 4-го порядка (ядро гомоморфизма). Столбцы заполняются произведениями ведущих представителей классов на элементы группы Н. После заполнения столбцов выполняется сравнение классов. Если составы левых и правых классов совпадают, то говорят просто о классах смежности и обозначают Н = К0, К1, К2, К3, К4, К5. При этом подгруппа Н называется нормальной. Ведущим представителем очередного класса при заполнении таблицы выбирается наименьший элемент G, из не вошедших в уже построенные классы.

Полученные классы смежности далее рассматриваются как элементы новой группы, называемой факторгруппой группы G по подгруппе Н (обозначается факторгруппа G =G/H). Операцией в этой новой группе является умножение классов: для каждой пары классов, например, К3×К5 = К2 строится таблица 4×4, в которой строки помечаются элементами первого сомножителя, а столбцы — второго. Далее выполняют умножение как в группе G. Результат такого умножения дает 16 элементов, но все они принадлежат одному классу, в нашем случае классу К2.

Кроме отображений изоморфизмов гомоморфизмами являются эндоморфизмы и автоморфизмы. Гомоморфизм группы G в себя называется эндоморфизмом, а изоморфизм группы G на себя- автоморфизмом. Эти понятия сопоставимы с понятиями отображений неструктурированных множеств инъекцией, сюръекцией и биекцией.

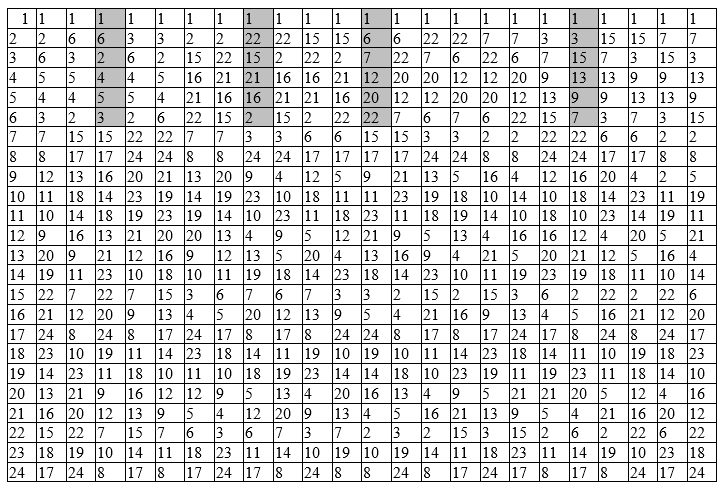
Таблица 2 — Кели симметрической группы $inline$S_4 (умножение Р_k = Р_i · Р_j)$inline$

Коммутант

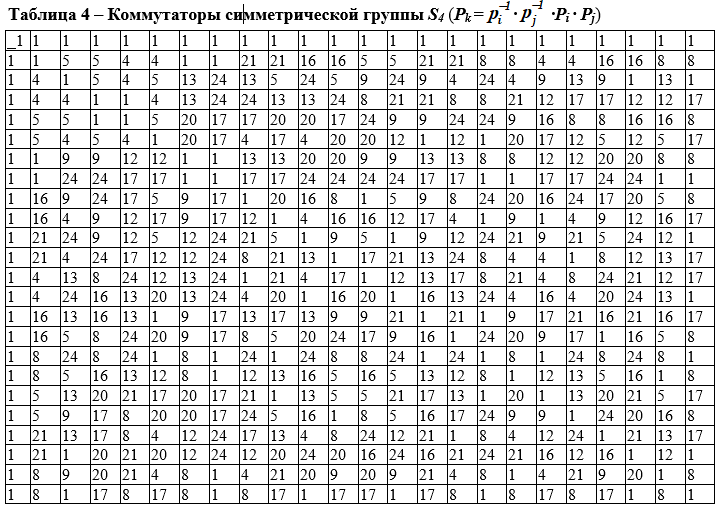
Каждой паре элементов а, b ∊ G сопоставим элемент, называемый коммутатором этой пары [a, b] = a -1b -1ab. Подгруппа К группы G, порожденная всеми ее коммутаторами, называется коммутантом группы G или производной подгруппой.

Группа G называется разрешимой, если цепочка G ⊇ G' ⊇ G'' ⊇… ⊇ G (i)⊇…, где каждая подгруппа G (i)является коммутантом предыдущей, обрывается после конечного числа шагов на единичной подгруппе, например, G (е)= 1.
В таблице 4 знакопеременная подгруппа G' =А4 порядка 12 — нормальная, из G = $S_4$ порядка 24, так как левый и правый смежные классы по этой подгруппе совпадают (классы это одно и тоже дополнение до полной группы $S_4$ ). Таблица 4 при этом сворачивается в меньшую 4×4 таблицу (коммутант), содержащую элементы G'' ={1,8,17,24} новой подгруппы, коммутант которой равен 1. Таблица 4 иллюстрирует разрешимость группы $S_4$ .

Заключение

В статье рассмотрены некоторые основные положения теории групп, которые часто используются в публикациях технического (не теоретико-математического) характера. Понимание текста таких публикаций во многом определяется владением математическим инструментарием.

Для группы приводится пример и техника гомоморфного отображения её в факторгруппу.
Числовые примеры призваны служить обеспечению доступности излагаемого материала и в большой мере помогают его пониманию и усвоению, при внимательном их разборе или даже повторении с карандашом в руках. Что в классических руководствах просто отсутствует. Часто объясняют это экономией места и времени.
Ожидаю реакции читателей, по которой станет понятно, продолжать ли в этом стиле или нет.

Литература

Авдошин С.М., Набебин А.А. Дискретная математика. Модулярная алгебра, криптография, кодирование. — М.: ДМК Пресс, 2017. -352 с.
Акимов О.Е. Дискретная математика.Логика, группы, графы- М.: Лаб.Баз. Зн., 2001. -352 с.
Андерсон Д.А. Дискретная математика и комбинаторика.- М.: Вильямс, 2003. -960 с.
Берлекэмп Э. Алгебраическая теория кодирования. -М.: Мир,1971.- 478 с.
Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 1- СПб.: ВКА им. А.Ф. Можайского, 2015. -219 с.
Ваулин А.Е. Дискретная математика в задачах компьютерной безопасности. Ч 2- СПб.: ВКА им. А.Ф. Можайского, 2017. -151 с.
Горенстейн Д. Конечные простые группы. Введение в их классификацию.-М.: Мир, 1985.- 352 с.
Грэхем Р., Кнут Д., Пташник О. Конкретная математика.Основание информатики.-М.: Мир,1998.-703 с.
Елизаров В.П. Конечные кольца. — М.: Гелиос АРВ,2006. — 304 с.
Иванов Б.Н. Дискретная математика: алгоритмы и программы — М.: Лаб.Баз. Знаний., 2001. -280 с.
Иерусалимский Я.М. Дискретная математика: теория, задачи, приложения — М.: Вузовская книга, 2000. -280 с.
Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.1 -М.: Мир,1988. — 430 с.
Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т.2 -М.: Мир,1988. — 392 с.
Ляпин Е.С., Айзенштат А.Я., Лесохин М.М., Упражнения по теории групп.- М.: Наука,1967.-264 с.
Муттер В.М. Основы помехоустойчивой телепередачи информации. -Л. Энергоатомиздат,1990.- 288 с.
Набебин А.А. Дискретная математика.- М.: Лаб.Баз. Знаний., 2001. -280 с.
Новиков Ф.А. Дискретная математика для программистов.- СПб.: Питер, 2000. -304 с.
Холл М. Теория групп.-М.: Изд. ИЛ, 1962.- 468 с.
Шиханович Ю.А. Группы, кольца, решётки. — СПб.: Кирцидели,2006. — 368 с.
Шнеперман Л.Б. Курс алгебры и теории чисел в задачах и упражнениях: В 2-х ч Ч.2.-Мн.: Выш. шк., 1987. -256 с.
Шнеперман Л.Б. Сборник задач по алгебре и теории чисел.- Минск: Дизайн ПРО, 2000. -240 с.