Математическая версия игры «Морской бой»
Несмотря на то, что является неплохим таким развлечением на долгий вечер, как и многие настолки, имеет практическую пользу в обучении математике: помогает подружиться с концепцией графика функции или уравнения, играется в любом классе, начиная с седьмого; или младше -, но тогда надо объяснить ученику идею координатной плоскости и линейной функции. Правила придуманы на основе классического морского боя.
В качестве игрового поля берётся координатная плоскость хОу произвольного размера. Если играющие знакомы с отрицательными числами, то от (-10; -10) до (10; 10) скорее всего будет достаточно, хотя чем обширнее их знания алгебры, тем больше нужна игровая площадь. Для всех, кто младше шестого класса, советую поле от (0; 0) до (20; 20), или даже до (10; 10). Прямоугольное, естественно (квадратность не обязательна). Для старших, конечно, можно задавать её как любую криволинейную трапецию или не задавать вовсе, лишь бы все корабли вместились в чертёж заданного масштаба.
Раскладка кораблей и подобные детали — как в стандартных правилах. Точно так же делаем у себя два поля (одно своё, одно противника). Можно играть «в открытую», показывая противнику свои корабли — это не сильно упростит ему жизнь, но сделает игру поучительнее.
Очерёдность ходов определяется стандартными правилами. А вот ходить можно по-всякому. Для семиклассников и младше всё просто: либо координаты точки, либо уравнение прямой (но — чтобы сходить, надо построить её график на поле противника). Продвинутые, естественно, могут использовать модули и кусочные функции. Дальше противник строит у себя этот же график и говорит, в каких точках поражены его корабли. Следует отметить, что если функция касается корабля, то он не ранен, и лишь если пересекает его — тогда ранен. Однопалубному кораблю достаточно одного пересечения для «убийства», четырёхпалубному — четырёх, и т.п., как в классических правилах.
Начиная с восьмого класса игра становится веселее и зрелищнее. Можно строить параболы и векторы! И гиперболы, конечно. А в десятом появляются синусоиды. Тангенсоиду применять нельзя — уж больно смертоносна она. Вообще, конечно, если игрок вспомнит, что sin10x хорошо так растягивается вверх, он и синусом всех убьёт, но лично я оставляю это как чит-код, догадаться до которого — похвально. Однако, конечно, запретить все периодические функции — правильная мысль. Здесь вводится ограничение — функцию каждого типа (квадратичную, линейную и так далее) можно использовать один раз в некоторое количество ходов, определяемое разнообразием функций в арсенале игроков; но, однако, лично я считаю разные способы задать линейную функцию как разные функции: можно задать «как обычно» (y = kx+b), можно как график уравнения (ax + by +c = 0), или можно использовать модуль или кусочную запись.
Получается довольно азартно, хотя и медленно. Часового занятия (играю с учениками, которых учу математике) не хватает на то, чтобы полностью разыграть партию, но как правило определяется побеждающая сторона. Можно играть по интернету с помощью онлайн-доски, поддерживающей множественные фреймы и выбор фона, например — google jamboard. Думаю, можно играть и в сингл-режиме, сначала создавая поле кораблей, а затем «раскатывая» его разными графиками.
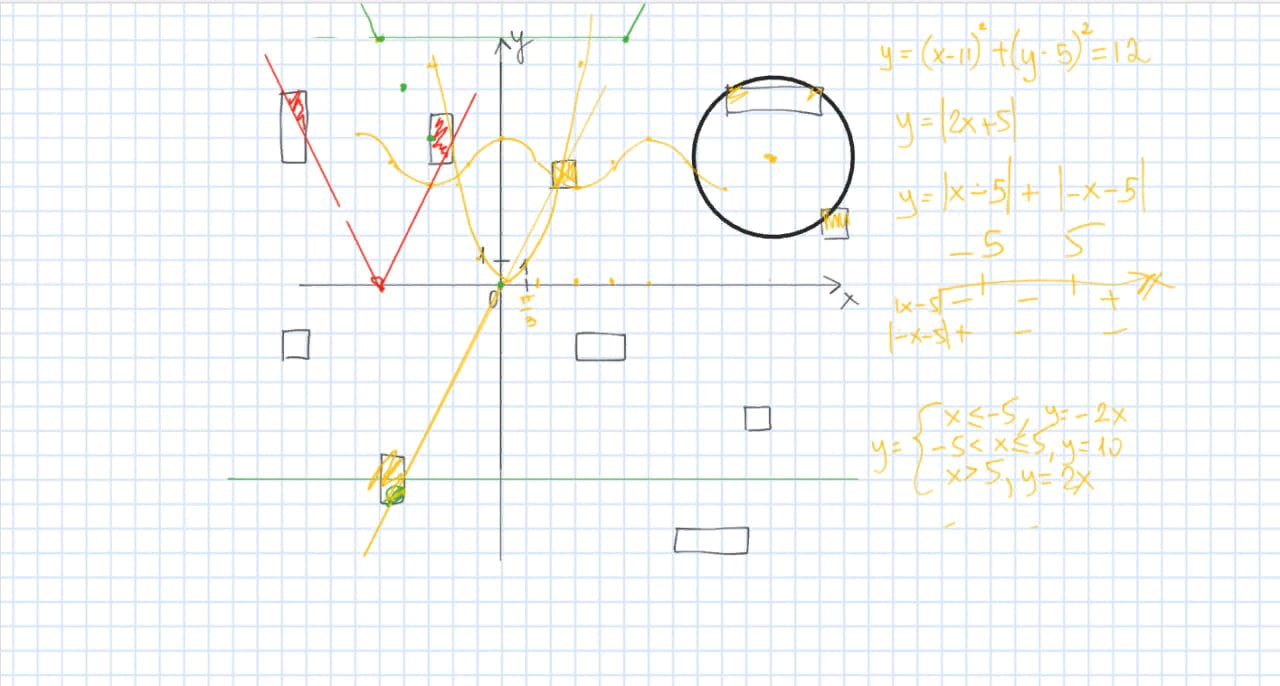
На первом примере две модульные функции, окружность (заданная уравнением), снусоида, парабола и две линейных. Каждая сделана в отдельный ход, между модульными и обычными линейными — цикл в 4 хода.
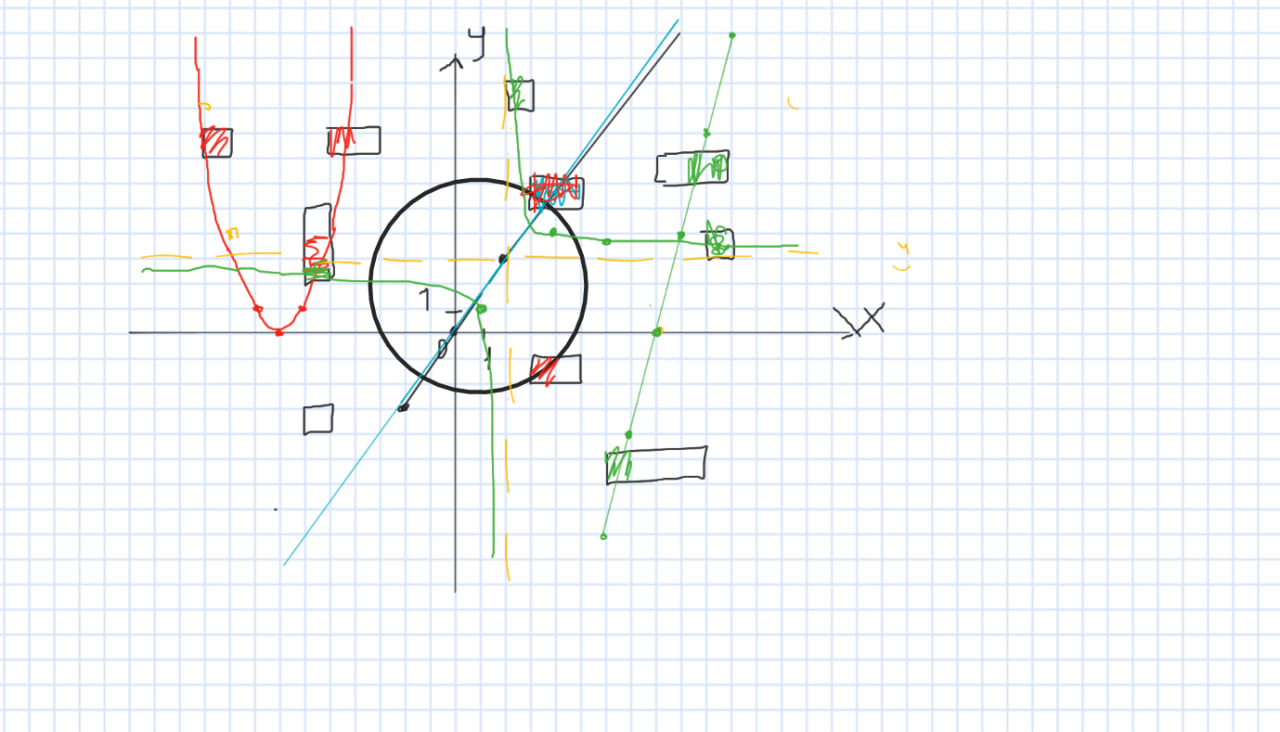
На втором примере есть ещё и гипербола. Несложно заметить, что тут всего четыре графика против шести на предыдущем: играли онлайн, один игрок по невнимательности сделал ход против себя (перепутать фреймы несложно).
