Математическая продлёнка. Математика кривого пропеллера04.05.2023 13:32

Отчего «гнётся и рвётся» пропеллер на фото и видео вы, наверняка, знаете. А какую именно форму принимают лопасти винта? Как зависит их видимая форма от скорости вращения? И причём здесь гиперболы?

Мой сын очень уважает самолёты. Особенно, турбовинтовые: здорово же, когда видно как работает двигатель и как вертится пропеллер! А какую интересную форму принимают винты при съёмке на телефон или цифровую камеру! Класс!

Красота!

Я полностью разделяю энтузиазм сына, И сегодня хочу подробнее рассмотреть математическую составляющую причудливого поведения пропеллеров, которое можно наблюдать на фото и видео.

Уверен, что для большинства читателей, в принципе, ничего особенно сложного в объяснении этого визуального эффекта нет. Развёртка светочувствительной матрицы цифровой камеры работает подобно щелевому затвору и круговое движение винтов «рисуется» на матрице с постоянным дрейфом, как показано на анимациях. По мере увеличения скорости вращения винта, видимое искривление увеличивается, появляются разрывы и дополнительные линии.

Об этом эффекте есть и многочисленные заметки в сети и ролики в Youtube, в общем, на качественном уровне всё понятно. Меня же заинтересовало не то, что лопасти «изгибаются» и даже «рвутся», а то, что в искривлённых формах легко угадываются кое-какие образы, хорошо знакомые тем, кто занимался дифференциальными уравнениями и теорией динамических систем. Приглашаю заглянуть в эту задачу поглубже.

Для начала выведем уравнение для видимых точек двухлопастного пропеллера, математической моделью которого может быть вращающаяся прямая, описываемая параметрическим уравнением:

\begin{align}&x = u\cos(\omega t),\\&y = u \sin(\omega t).\end{align}

Роль щелевого затвора может играть вертикальная прямая, двигающаяся горизонтально со скоростью v и уравнением x = vt. Точки пересечения этих двух прямых образуют кривую, с параметрическим уравнением:

\begin{align}&x = vt,\\&y = vt \, \mathrm{tg}(\omega t).\end{align}

На этом этапе пора навести в уравнениях порядок. Введём масштаб времени 1/\omega и длины v/\omega и приведём уравнения к безразмерному виду:

\begin{align}&x = \tau,\\&y = \tau \, \mathrm{tg}(\tau).\end{align}

Перейдя от параметрического представления кривой к явному виду получим чрезвычайно простое уравнение для видимых лопастей:

y = x\, \mathrm{tg}(x).Вот она форма лопасти!

Вот она форма лопасти!

Если лопастей N штук, то кривые для них будут отличаться фазой под тангенсом:

y = x\, \mathrm{tg}\left(x-\frac{2\pi}{N}n\right).

Вот, например, как будет выглядеть пропеллер с пятью лопастями и переменной фазой (чтобы «лопасти» закрутились):

Здорово! Работает! Но это ещё не всё. Обратите внимание, при обезразмеривании задачи исчезли оба параметра: частота вращения ω и скорость затвора v. Это говорит о том, что решение задачи автомодельно,  то есть, изменению любой из этих скоростей соответствует изменение масштаба длины, но форма кривых останется точно такой же.

При увеличении скорости вращения винта, уменьшается отношение , что соответствует уменьшению масштаба нашего автомодельного решения. Оно, как бы, сжимается, оставаясь в пределах диска, заметаемого пропеллером.

При увеличении скорости вращения винта, уменьшается отношение v/\omega, что соответствует уменьшению масштаба нашего автомодельного решения. Оно, как бы, сжимается, оставаясь в пределах диска, заметаемого пропеллером.

Глядя на то, как меняется видимая форма лопастей можно обратить внимание на то, что кроме неподвижной точки в центре пропеллера есть ещё одна особая точка с координатами (0,-1). Присмотритесь, проходя через неё, кривые терпят разрыв и становятся похожими на гиперболы. Человек, искушённый в дифференциальных уравнениях, узнает в ней гиперболическую особую точку или седло. Откуда она тут и о чём говорит её существование?

Давайте перейдём от кривых, в которые превращаются лопасти, к полю скоростей, по которому двигаются траектории точек лопасти. Для этого продифференцируем параметрические уравнения траектории:

\begin{align}&\dot{x} = 1,\\&\dot{y} = \mathrm{tg}(\tau) + \frac{\tau}{\cos^2(\tau)} = \mathrm{tg}(\tau) + \tau+\tau\,\mathrm{tg}^2(\tau).\end{align}

А теперь выразим \tau и \mathrm{tg}(\tau)через x и y: \tau = x,\ \mathrm{tg}(\tau) = y/x, и подставим в систему дифференциальных уравнений, превратив её в автономную систему (не зависящую от времени явно):

\begin{align}&\dot{x} = 1,\\&\dot{y} = \frac{1}{x}(y+x^2+y^2).\end{align}

Наконец, можно привести её к более удобному для анализа, виду, изменив динамику, то есть скорости точек вдоль траекторий, но оставив без изменений сами траектории:

\begin{align}&\dot{x} = x,\\&\dot{y} = y+x^2+y^2.\end{align}

Стандартный анализ особых точек этой системы, в которых обе производные обращаются в ноль, даёт нам два стационарных решения: вырожденный отталкивающий узел (звезду) (0,0), и гиперболическую (седловую) точку (0,-1).

Вот как выглядит поле направления скоростей для этой системы со стационарными точками:

Узел показан зелёным цветом, а седло -- красным.

Узел показан зелёным цветом, а седло — красным.

А вот её фазовый портрет, отражающий типичные траектории системы (синие линии) и её инвариантные многообразия (чёрные линии).

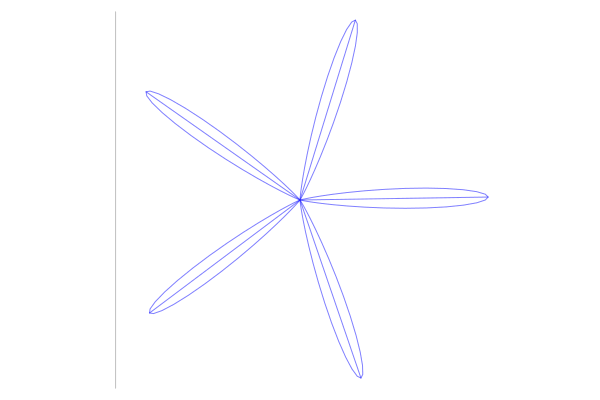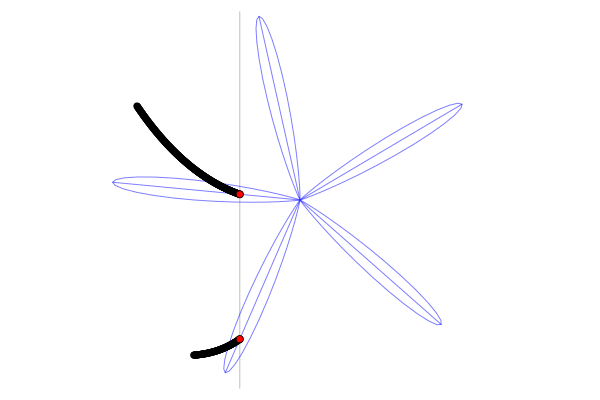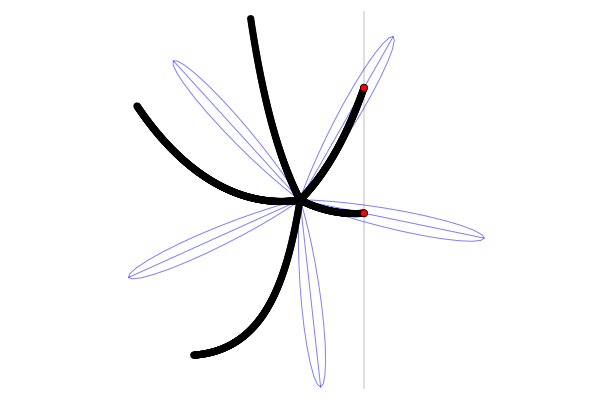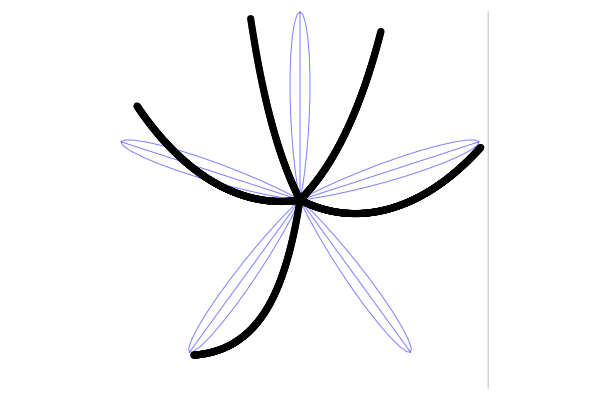
А вот её фазовый портрет, отражающий типичные траектории системы (синие линии) и её инвариантные многообразия (чёрные линии).

Вот откуда взялись гиперболы и разрывы у «кривых» лопастей на снимках! Поглядите сами на то, как видимые точки пропеллера следуют полю скоростей. В тот момент, когда пропеллер проходит через седловую точку, линия и винта совпадают, и единственная точка пересечения превращается в полный отрезок прямой. В этом случае мы получим снимок всей лопасти пропеллера без искажений.

Сын-восьмиклассник, конечно, не всё понял из того, что я ему рассказал, но картинки ему понравились, и в Desmos он смог построить кривые y = x\,\mathrm{tg}(x-a)и анимировав параметр a, сам увидел во что превращаются лопасти. А осознав существование седловой точки, развидеть он её уже не может и отыскивает на фотографиях и видео.

© Habrahabr.ru