Маленькие задачи по физике26.04.2020 16:33

Приведу несколько задач, в основном из физики. Мне они нравятся. Надеюсь они понравятся и Вам.

Забудем о черных дырах, темной энергии и материи; забудем о коте Шредингера, большом взрыве и эволюции Вселенной; забудем о струнах и суперструнах; и даже о фракталах забудем. В этих темах, как и в политике, большинство считает себя возможным высказаться. И высказываются. И много говорилось и говорится дельного, а еще больше говорилось и говорится путаницы и просто нелепицы. Каюсь, к этому и я приложил руку. А давайте вернемся к простоте классической физики и к ее понятным задачам. Иногда полезно спуститься с небес на землю.

Для большинства задач я не привожу решения. Самое полезное — найти самому решение. Конечно, задачи не для профессионального физика, исключая задачу о ленте и о пушке.

Большинство задач, так или иначе, обсуждалось в Internete. Но время идет и приходят новые поколения и, может быть, для них задачи будут в новинку.
Я айтишник. Тогда почему пишу о физике? По образованию я физик. Когда сменил профессию, то с большим энтузиазмом начал проектировать и программировать. Мне грезилось, что лет за двадцать-тридцать программирование так шагнет вперед, что не нужно будет реализовывать алгоритм в деталях, а нужно будет только описывать постановку задачи. И что я вижу по прошествии тридцати лет? Я достиг возраста, когда можно и побрюзжать. И я так и сделаю. Если судить по рубрике «лучшие публикации » Хабра, то программирование во многом топчется на месте. То же вечное копание в языках программирования, осложненное тем, что их число выросло на два порядка (навскидку). Добавилась беда словоблудия псевдоанглицизмов:

шефердить пропозал, фичи, баги и пропертя, хакатон, фронтенд и бэкенд, хадуп, лид, ярд, разраб, митинг, чо напилил, вjobывать, гайд-бук, ревью, пушить; есть кодоанализатор, но работает он не по пушу (и уж тем более не в момент написания кода), а с сильным запозданием и проверяет не на том уровне что всякие sonar cube и прочие pvs. пул-реквест; не делать ничего от слова совсем, ЕГАИС, пофиксить, офер, сабж. сама по себе БСП это отличная вещь (как и БПО и БИП), миста, фьюж, ЗУП, рептилойды, клюшкина ЗиК, трэш, из всех типовых конф меньше всего всегда вмешивался в код именно ЗуП/ЗиК и их модули в УПП/КА, чувак открывает пуллреквест, чувак назначает себя ревьювером, чувак пишет LGTM, чувак мержит код, это будет деанон, скилл, легаси, аутстафе, тикет, я проэстимировал таску в два дня, фетчить; скоуп задачи теперь позволял мне слегка отрефакторить болото, полное говна, в котором я всё время плаваю; сабметод, почти сотня человек в аутстафе (половина всей компании) оказалась «в ожидании нового проекта», cчитай — лимбически безработными.

Эти перлы игры в форму я выбрал всего из двух статей Хабра и комментариев к ним. И, похоже, этот стиль одобряется Хабром. И, похоже по умолчанию, что лох тот, кто этого стиля не придерживается. Классика не в почете у постмодерна. Да, описанный стиль мне напоминает некое крикливое, приниженное подобие стиля постмодернизма. По этому поводу есть прекрасная книга «Интеллектуальные уловки. Критика современной философии постмодерна». Авторы Жан Брикмон, Ален Сокал. Особенно хорошо в ней «Приложение А. Нарушая границы: к трансформативной герменевтике квантовой гравитации». Так и хочется написать статью «Нарушая границы: к трансформативной герменевтике языков программирования». Но, увы, талант не тот.

А ведь в физике и математике несравненно больше поводов насытить язык терминологическими новациями (бордизмы, кобордизмы, гомотопии, гомологии, когомологии…). И в физике и математике английский, несомненно, не в меньшей мере применяется чем в программировании.

Но почему то в физике и математике нет такого англизированного поноса как в программировании. Физики и математики сохраняют человеческий язык и без нужды не выпендриваются. А если вводят термин, то четко его определяют и обосновывают его необходимость.

В общем, я разочарован прогрессом в программировании. Может деньги его тормозят? Может тормозит очень низкий порог вхождения, когда почти любой юнец быстро начинает «ваять», зарабатывать и учить других с «легкостью в мыслях необыкновенной». Каюсь, и со мной так было. Меньше чем за год программирования, я уже был руководителем проекта и думал, что я ухватил бога за бороду. Но скоро я вернулся к реальности. Прошли десятилетия, а я, к сожалению, не вижу большого прогресса в программировании. «А воз и ныне там». А вот в физике за последние тридцать лет сделано столько всего: открытие ускоренного расширения Вселенной, теория струн и суперструн, квантовый компьютинг… И, главное, появилась стандартная модель.

Удрученный застоем в основах информатики, я предпочитаю писать статьи по физике, математике, а не статьи по программированию.

Для затравки начнем совсем с элементарных задач и задач не из физики. Их решение даст повод поразмышлять о причудах интеллекта.

Букварь Арнольда

Российский математик Арнольд привел такую задачку.

У Маши не хватало для покупки букваря семи копеек, а у Миши одной копейки. Они сложились, чтобы купить один букварь на двоих, но денег все равно не хватило. Сколько стоил букварь?

Если ответ не приходит быстро в голову, то вы уже не дитя. И я убедился, что уже далеко не дитя. Увы, ответ не пришел мне мгновенно.

Арнольд говорил, что чем более важный и остепененный был человек, тем медленнее он решал эту задачу. Похоже, что многознание мешает быстрому непосредственному мышлению, а предпочитает применить шаблон опыта.

Толстой и три шапки

Продавец продаёт шапку. Стоит 10 р. Подходит покупатель, меряет и согласен взять, но у него есть только банкнота 25 р. Продавец отсылает мальчика с этими 25 р. к соседке разменять. Мальчик прибегает и отдаёт 10+10+5. Продавец отдаёт шапку и сдачу 15 руб. Через какое-то время приходит соседка и говорит, что 25 р. фальшивые, требует отдать ей деньги. Продавец возвращает ей деньги. Cколько потерял продавец?

(По легенде, эта задачка придумана Львом Толстым для второго класса церковноприходской школы (ЦПШ). Сейчас её правильно могут решить только 30% старшеклассников, только 20% студентов ВУЗов и только 10% работников банков и кредитных учреждений.)

Когда-то давно, я рассказал об этой задаче программистам у себя на работе. Что ни человек, то разный ответ. Один руководитель проекта насмерть сражался за свой неправильный ответ. А разрабатывал он в своем проекте и бухучет. Так вот, в конце-концов, он составил журнал банковских проводок, подбил баланс и пришел к правильному ответу.
Ну и как вам нравится уровень 2-го класса ЦПШ!

А теперь переходим к физике.

Вольт в степени ампер

Из математики мы знаем, что умножение определяется через сложение. Например:
$4*3=4+4+4$

Но почему тогда в физике вольт можно умножать на ампер, но вольты с амперами нельзя складывать. Какая физика препятствует этому?

Более того, можно вольт делить на ампер, а вот складывать и вычитать нельзя.

Аналогично, степень определяется через умножение. Например: $ a^3= a*a*a$ . Тогда почему нельзя возводить вольт в ампер?

Возможна ли такая ситуация: я подаю напряжение $U$ на черный ящик, замеряю ток $I$ в цепи, замеряю данное на выходе и получаю, что оно изменяется как функция $I^U$ ? Ответ с точки зрения математики, я нашел в книге Бриджмена «Анализ размерностей» и в книге Когана «Размерность физической велич
ины»(написана явно по следам Бриджмена). К своему стыду я приведенного ответа не знал.
Но все равно, я не могу принять его физически. Где, физическая, а не математическая аргументация?

Рассуждения Бриджмена почти убеждают. Но, а если я посажу в черный ящик, человека с аккумулятором и реостатом…(что еще надо?) и он в ответ на I и U на входе, он на выходе дает $I^U$ . Все это можно сделать. Опровергает ли это построения Бриджмена? Можно возразить что это не естественный пример. Хорошо, уберем человека из черного ящика и посадим на его место автомат с программой $I^U$ . А это опровергает ли построения Бриджмена? Мне скажут, что это опять искусственный прибор. Но это, если знать устройство черного ящика. Или, может, удовлетвориться ответом, что если мы имеем дело с прибором, то нужно сделать вывод, что это не натуральное устройство, а искусственное, которое, поэтому, не подвластно естественным законам?

В какой бильярд труднее играть в большой или маленький?

И шары и кии и лузы и стол, бильярда уменьшены в одинаковой степени. Бильярдист не изменился. В какой бильярд труднее играть в большой или маленький?

Землетрясения и земная ось

Может ли сдвинуться земная ось в результате землетрясения? Может ли измениться продолжительность суток в результате землетрясения?

Вот информация из масс-медиа.

11 марта 2011 года землетрясение магнитудой 8,9 произошло в Японии. Его эпицентр находился в 373 километрах северо-восточнее Токио, а очаг залегал на глубине 24 километров.
Специалист Лаборатории реактивного движения (JPL) НАСА Ричард Гросс (Richard Gross) считает, что землетрясение могло привести к смещению оси Земли примерно на 15 сантиметров в сторону 139-го градуса восточной долготы. Продолжительность дня должна сократиться на 1,6 микросекунды.
Специалисты Национального института геофизики и вулканологии Италии сообщили о том, что, по их расчетам, в результате землетрясения ось сместилась почти на 10 сантиметров.
27 февраля 2010 года землетрясение магнитудой 8,8 произошло в Чили. Исследователь лаборатории реактивного движения NASA Ричард Гросс предположил, что в результате подземных толчков, вращение Земли изменилось. Используя сложную модель, Гросс вместе с группой ученых рассчитал, что землетрясение могло сократить каждый земной день на 1,26 микросекунды. Кроме того, землетрясение отклонило ось вращения Земли на 2,7 мс (в проекции на поверхности около 8 см).
По данным лаборатории реактивного движения НАСА (США), в результате землетрясения протяженность суток сократилась на 6,8 микросекунд, а земная ось сместилась примерно на 7 сантиметров.

А что думает по этому поводу физика? Рассматриваем систему отсчета с началом в центре Земли и неподвижную относительно звезд. Как мы знаем из физики она достаточно инерциальна. Тогда ось вращения Земли совпадает с прямой, вдоль которой направлен вектор момента количества движения Земли. Из физики известен закон сохранения момента количества движения. Согласно ему, никакие внутренние пертурбации в системе не меняют момента количества движения этой системы. Значит, никакой внутренний земной катаклизм не меняет момента количества движения. Вот если он становится внешним, то дело другое. Примеры катаклизмов, носящих внешний характер: падение астероида, выброс части Земли в Космос, гравитационное воздействие Луны.

Итак, ось не может сместиться в результате землетрясения на Земле, если только не произошло выброса в космос. Но вот кора земная или лед на полюсе могут сдвинуться. И если на полюсе был воткнут флаг, то в результате землетрясения, он может оказаться уже воткнутым не точно на полюсе. Но это сдвинулась не ось, а сдвинулась поверхность.

Далее, если не меняется момент количества движения, то и угловая скорость не изменится и, значит, не изменится и продолжительность суток.

Юла в миске

Занимаю годовалого внука, запуская юлу. Она убегает то под диван, то под стол. Надоедает ползать за ней. Начинаю пускать её в круглой миске, чтобы юла не убегала.

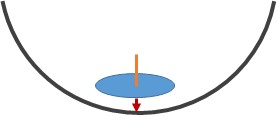
Обнаруживаю эффект вылета юлы из миски: если миску немного качнуть по кругу, то юла начинает с ускорением взбираться по стенке и иногда стремительно вылетает из миски. Собственный момент переходит в орбитальный. Что за механизм этого перехода?
Миску желательно брать с дном плавно сопрягающимся со стенками. Для получения эффекта обычно нужно попробовать несколько раз.

Камень пробивает лед

Начало зимы. На пруду тонкий, свежий, гладкий лед. Беру камень и швыряю его на лед, чтобы пробить его. Если камень пробивает лед, то виден эффект круговой воздушной волны — расходящееся кольцо-пузырь, в конце концов, распадающееся на отдельные пузыри.

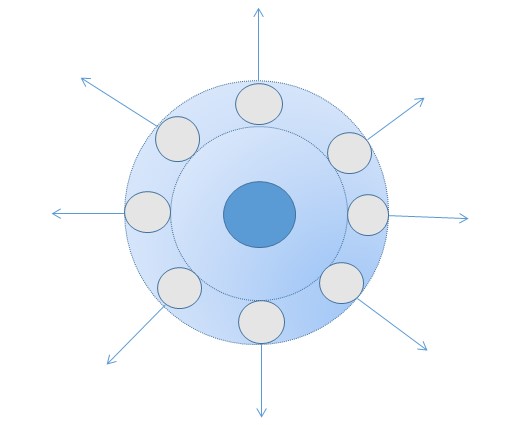
Как и почему кольцо-пузырь образовывается? Захват каменем воздуха за собой? Нет. Это я экспериментально проверил: даже если камень застревает во льду и препятствует проникновению воздуха, картина остается такой же, как и при проникновении камня через лед.

Сопутствующие вопросы:

Когда круг распадется на пузыри?
С какой скоростью расширяется круг?

Ложка сахара

Любая физическая задача для своего практического решения требует некоторого упрощения. Так при движении брошенного рукой камня, можно пренебречь силой трения камня о воздух. Далее, для уточнения, можно ввести трение пропорциональное скорости камня. А потом можно ввести и квадратичный по скорости член. И уже такую модель проще исследовать на компьютере. А еще нужно учесть изменение силы гравитации с высотой. А еще нужно учесть изменение плотности воздуха с высотой… Поэтому можно говорить о некоей иерархии упрощений. Для каждой точности, требуется своя иерархия упрощений.

Но для некоторых задач эту иерархию мне не удалось определить.

Вот два примера.

Сколько максимально сахара можно зачерпнуть ложкой практически? Теоретически — бесконечно. Но физика — это учет реальности: сыпучесть, дрожание руки, сосуда, воздуха, наклон ложки, форма частиц сахара… Я не мог предложить простую реалистичную модель. А Вы сможете?

Аналогичная задача: стопка домино в которой каждая костяшка, сдвинута по отношению к нижней. Получается стопка с наклоном в сторону сдвига, так что костяшки сдвигаются все больше, по отношению к нижней. Теоретически сдвиг верхней костяшки можно сделать бесконечным по отношению к нижней костяшке.

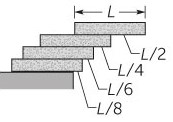
А в реальности какой возможный максимальный сдвиг?

«Просто Землю вращают, куда захотят, наши сменные роты на марше»

Незабываемый первый курс физфака БГУ. Общага. Вечер в 113 комнате. Легли спать. Начался треп на всякие темы. Появляется такая задача. Прыгнул кузнечик. Вот он приземляется, но не останавливается, а сразу опять отталкивается и т.д. И все в одну сторону. Каждый раз он толкает землю как у Высоцкого роты. Спрашивается, как сильно он сможет раскрутить землю при сколь угодно большом времени своих прыжков? Ну, а потом можно перейти и к ротам Высоцкого.

Долго обсуждаем, спорим, потом раздается голос:» А как с сохранением момента количества движения для замкнутой системы?» И всем стало ясно.

Однако каков силовой механизм, который мешает бесконечной раскрутке?

По ветру быстрее ветра или прок от богатства

Может ли яхта плыть быстрее ветра?

Этот вопрос мне задал по телефону мой племянник бизнесмен. Я возмутился и сказал, что это бред. А в ответ: у моего знакомого есть яхта и он утверждает, что можно плыть быстрее ветра. Скоро я понял в чем дело.

Этот случай заставил меня задуматься вот о чем. Оказывается богатому практически доступны некоторые вещи, которые бедному теоретику кажутся абсурдными. Став богатым, мой племянник стал мыслить раскованнее, шире. Он стал более интересным. Раскованность мышления привела его бизнес в Германию, где он предложил фирме хитроумную схему ухода от налогов. Немцы на него изумленно посмотрели и покрутили у виска рукой: закон нельзя обходить!

Скоро Германия ему надоела и он вернулся в РБ. Теперь он о немцах отзывается почему-то, не иначе как с эпитетом «квадратные».

Острая волна на воде или прок от созерцания

Тот кто сидел на рыбалке или просто так на берегу озера и наблюдал за его поверхностью в неветреный день, наверняка видел эффект острой волны: иногда на поверхности воды возникает возбуждение и в виде острого клина (конус Маха?), бежит по воде прямо или с искривлением, и через мгновение пропадает. Похоже на то? как от щуки убегает рыба по поверхности воды. Но как я ни пытался обнаружить что-нибудь предметное на острие клина, ничего не обнаружил. Скорость острия клина — раз в десять больше скорости обычной круговой волны на воде. Описания эффекта не нашёл ни в одной монографии по гидродинамике. Так когда и как образуется клиновидная волна на воде?

Пушка и ОТО

Это задача Фейнмана. С Земли выстреливают вертикально вверх из пушки снаряд с атомными часами. В конце-концов он падает на Землю. Достают часы и сверяют с земными. Какие часы будут отставать из-за эффектов ОТО? Временем ускорения при выстреле пренебречь.

Некоторые доктора наук начинали вычислять, вычислять…

Для нефизиков скажу, что нужно привлечь принцип эквивалентности ОТО и доказанный факт, что чем сильнее гравитационное поле, тем медленнее идут часы.

Какой механизм столкновений, при котором установится распределение Максвелла?

В термодинамическом равновесии скорости молекул газа распределены по Максвеллу. А это распределение говорит, что могут быть молекулы со сколь угодно большими скоростями. Что за абсурд, хоть и маловероятный? И если даже признать наличие предела индивидуальной энергии молекулы, то как понять механизм неравномерного распределения? Например, стартуем от одинаковых скоростей. Начинаются столкновения, в результате которых, якобы, происходит перераспределение энергии. Обычно рассматривают упругие удары. Но при упругом ударе энергия измениться не может. А при неупругом энергия может только потеряться. Так какой же механизм столкновений, при котором установится распределение Максвелла? Как возникают большие скорости отдельных молекул?

Вектор скорости

Скорость есть вектор. Если точка участвует в двух скоростях, то результирующая скорость есть векторная сумма этих двух скоростей. Этим воспользовался Галилей, при определении скорости тела, брошенного под углом к горизонту. Это движение есть суперпозиция двух движений — вертикального, управляемого силой тяжести и горизонтального — движения по инерции.
А теперь рассмотрим движение стрелы в луке. Стрела упирается в середину тетивы. Половина тетивы тянется к одной вершине лука, а другая половина тянется к другой вершине лука. Значит движение основания стрелы есть суперпозиция двух указанных движений.

Соответственно результирующая скорость основания стрелы (да и всей стрелы) есть векторная сумма скоростей движения к концам лука. А теперь представим, что мы очень сильно растянули лук, так что можно считать, что половинки тетивы почти параллельны и скорости их движения равны v. Тогда результирующая скорость равна 2v, а это значит, что стрела должна оторваться от тетивы. Абсурд. Так в чем дело?

Откуда взялась энергия?

Я и мой сын едем в деревню на автомобиле. Сын задает мне вопрос. «Вот мы едем со скоростью v. Пусть у меня в руках камень массой m. Я бросаю его вперед со скоростью v. До броска камень имел кинетическую энергию $mv^2/2$ относительно земли. При броске я ему добавил такую же энергию . Значит, исходя из энергетического баланса, общая кинетическая энергия у него будет $mv^2/2 + mv^2/2 = mv^2$ . В то же время вычислим кинетическую энергию по определению этой энергии: $m(2v)^2/2 =2mv^2$ . Разница с первым подходом $mv^2$ . Парадокс. Балансовый подход не согласуется с кинетическим подходом от определения. В чем дело? Объясни, как физик по образованию »

Сходу объяснить парадокс я не мог. Удивился сам. Более того, решив потом задачу формульно, то бишь формально, я на уровне интуиции не могу согласиться с решением. Такая ситуация нередка (для среднего уровня мышления, видимо). Так, например, движение гироскопа следует из уравнений Ньютона. Но все равно, очень трудно объяснить почему не падает волчок исходя из силовой точки зрения, а не исходя из закона движения кинетического момента. И это только небольшой шаг от прямого применения законов Ньютона к применению следствий из этих законов. А что уж тогда говорить о статистической физике, например.

Расширение Вселенной

К стене прикреплена полоска резины длиною $l_0=1м$ , ее начинают растягивать с постоянной скоростью без разрывов до бесконечности, к моменту начала растяжения по ней начинает ползти точечная улитка (с конца ленты к точке привязки) со скоростью $v$ меньшей скорости растяжения $V$ , спрашивается: доползет ли она до края и за сколько времени?)

Эта задача появилась так. Была конференция по физике элементарных частиц. Обед. Физик-теоретик Л.Б. Окунь предлагает разным теоретикам решить приведенную задачу с целью проверки быстроты мышления теоретиков. А.Д. Сахаров выдал ответ за две минуты.

Мне понадобилось часа два, чтобы набросать решение, в котором, однако, я не был уверен. Потом я засомневался в правильности решения и потратил ещё два дня на приведение решения к аккуратному виду. Впрочем, в правильности решения на 100% я не уверен и сейчас.
Не правда ли, задача похоже на задачу движения космической ракеты в расширяющейся вселенной? Кстати и на растягивающейся ленте в любой ее точке будет наблюдаться эффект расширения — все окружающие точки убегают от нее.

Два дня назад взял в руки книгу Гарднера, мэтра занимательной математики, и обнаружил эту задачу в дискретном варианте. Да, ничто не ново под Луной».

А если улитка движется от точки привязки к другому концу?