Магия тензорной алгебры: Часть 18 — Математическое моделирование эффекта Джанибекова08.08.2015 20:48

Прошлая статья должна была быть о численном моделировании эффекта Джанибекова, но мне внезапно пришла в голову мысль, что этот эффект можно исследовать качественно, пусть и довольно приближенным первым методом Ляпунова. Однако, численное моделирование тоже весьма интересный вопрос, тем более лежащий в плоскости моих исследовательских задач. Поэтому, сегодня мы

Окончательно определимся с тем, как использовать параметры Родрига-Гамильтона для описание ориентации тела в пространстве
Рассмотрим формы представления уравнений движения свободного тела: покажем как тензорные уравнения можно превратить в матричные и компонентные.
Выполним моделирование движения свободного твердого тела при различных соотношениях между главными моментами инерции и покажем, как проявляет себя эффект Джанибекова.

Мы уже не раз рассматривали эти уравнения в векторном виде

$(1)$

$\begin{align*} &m \, \vec a_{c} = \sum \vec F_k^{\,e} \ &\mathbf I_c \, \vec\epsilon + \vec\omega \times \left(\mathbf I_c \, \vec\omega \right) = \sum \vec M_{c}(\vec F_k^{\,e}) \end{align*}$

Векторная форма записи удобна для общего анализа характера зависимостей, она привычна и в ней видно, что означает конкретное слагаемое. Однако, для дальнейшего преобразования уравнений в форму, удобную для моделирования, перейдем к тензорной записи

$(2)$

$\begin{align*} &m \, \left(\ddot x^{\,i} + \Gamma_{\,kl}^{\,i} \, \dot x^{\,k} \, \dot x^{\,l} \right) = X^{\,i} \ &I_{\,j}^{\,i} \, \dot\omega^{j} + \varepsilon^{\,ijk} \, \omega_{\,j} \, g_{\,kl} \, I_{\,p}^{\,l} \, \omega^{\,p} = M^{i} \end{align*}$

где $x^{\,i}$ — контравариантные координаты центра масс тела; $X^{\,i}$ — контравариантные компоненты главного вектора внешних сил, приложенных к телу; $M^{\,i}$ — контравариантные компоненты главного момента внешних сил, приложенных к телу.

Система уравнений (2) уже является замкнутой, интегрируя её можно получить закон движения центра масс и зависимость угловой скорости тела от времени. Но, нас ещё будет интересовать ориентация тела, поэтому дополним данную систему уравнений

$(3)$

$2 \, \varepsilon^{\,ijk} \, \lambda_{\,j} \, \dot\lambda_{\,k} + 2 \, \lambda_0 \, \dot\lambda^{\,i} - 2 \, \lambda^{\,i} \, \dot\lambda_0 = \omega^{\,i}$

Уравнение (3) есть ничто иное как представление компонент угловой скорости через параметры ориентации Родрига-Гамильтона. Это выражение мы уже получали в предыдущих статьях. Теперь мы будем рассматривать его как дифференциальное уравнение, связывающее параметры ориентации с компонентами угловой скорости.

Однако, параметры Родрига-Гамильтона являются избыточными — их четыре, а для описания ориентации тела в пространстве достаточно трех координат. И число неизвестных в системе (2), (3) превышает число уравнений на единицу. Значит нам придется дополнить уравнения (2) и (3) уравнением связи между параметрами ориентации. В статье о параметрах Родрига-Гамильтона мы показали, что поворот тела удобно описывать единичным кватернионом, что есть

$\lambda_0^2 + \lambda_1^2 + \lambda_2^2 + \lambda_3^2 = 1$

или, в тензорном виде

$(4)$

$\lambda_0^2 + \lambda_{\,i} \, \lambda^{\,i} = 1$

Продифференцируем (4) по времени

$2\, \lambda_0 \, \dot\lambda_0 + \dot\lambda_{\,i} \, \lambda^{\,i} + \lambda_{\,i} \, \dot\lambda^{\,i} = 0$

С учетом коммутативности скалярного произведения полагаем $\dot\lambda_{\,i} \, \lambda^{\,i} = \lambda_{\,i} \, \dot\lambda^{\,i}$ , тогда

$(5)$

$\lambda_0 \, \dot\lambda_0 + \lambda_{\,i} \, \dot\lambda^{\,i} = 0$

и есть искомое уравнение связи. Полная система уравнений движения свободного твердого тела в тензорной форме будет иметь вид

$(6)$

$\begin{align*} &\dot x^{\,i} - v^{\,i} = 0 \ &m \, \left(\dot v^{\,i} + \Gamma_{\,kl}^{\,i} \, v^{\,k} \, v^{\,l} \right) = X^{\,i} \ &2 \, \varepsilon^{\,ijk} \, \lambda_{\,j} \, \dot\lambda_{\,k} + 2 \, \lambda_0 \, \dot\lambda^{\,i} - 2 \, \lambda^{\,i} \, \dot\lambda_0 - \omega^{\,i} = 0 \ &\lambda_0 \, \dot\lambda_0 + \lambda_{\,i} \, \dot\lambda^{\,i} = 0 \ &I_{\,j}^{\,i} \, \dot\omega^{j} + \varepsilon^{\,ijk} \, \omega_{\,j} \, g_{\,kl} \, I_{\,p}^{\,l} \, \omega^{\,p} = M^{i} \end{align*}$

Довольно страшновато — (6) содержит 13 нелинейных дифференциальных уравнений первого порядка с 13 неизвестными величинами. Страшно выглядит из-за общей тензорной записи, но при переходе к конкретным координатам, в нашем случае декартовым, система (6) значительно упростится.
Введем вектор-столбец фазовых координат тела

$\mathbf y = \begin{bmatrix} \mathbf x^T && \mathbf q^T && \mathbf v^T && \mathbf \omega^T \end{bmatrix}^T$

где $\mathbf x = \begin{bmatrix} x_c && y_c && z_c \end{bmatrix}^T$ и $\mathbf v = \begin{bmatrix} v_{cx} && v_{cy} && v_{cz} \end{bmatrix}^T$ — положение и скорость центра масс тела; $\mathbf q = \begin{bmatrix} \lambda_0 && \lambda_1 && \lambda_2 && \lambda_3 \end{bmatrix}^T$ и $\mathbf \omega = \begin{bmatrix} \omega_x && \omega_y && \omega_z \end{bmatrix}^T$ — ориентация и угловая скорость тела.

В декартовом базисе метрический тензор представлен единичной матрицей, а символы Кристоффеля равны нулю, поэтому система уравнений (6) в матричной форме запишется так

$(7)$

$\begin{align*} &\mathbf{\dot x} - \mathbf v = \mathbf 0 \ & 2\, \mathbf B \, \mathbf{\dot q} - \mathbf D \, \mathbf \omega = \mathbf 0 \\ &m \mathbf{\dot v} = \mathbf X \ &\mathbf I_c \, \mathbf{\dot\omega} + \mathbf \Omega \, \mathbf I_c \, \mathbf \omega = \mathbf M_c \end{align*}$

где введены матрицы

$\mathbf B = \begin{bmatrix} \lambda_0 && \lambda_1 && \lambda_2 && \lambda_3 \ -\lambda_1 && \lambda_0 && -\lambda_3 && \lambda_2 \ -\lambda_2 && \lambda_3 && \lambda_0 && -\lambda_1 \ -\lambda_3 && -\lambda_2 && \lambda_1 && \lambda_0 \ \end{bmatrix}, \quad \mathbf D = \begin{bmatrix} \mathbf 0^T \ \mathbf E \end{bmatrix}, \quad \mathbf \Omega = \begin{bmatrix} 0 && -\omega_z && \omega_y \ \omega_z && 0 && -\omega_x \ -\omega_y && \omega_z && 0 \end{bmatrix}$

Разрешая систему (7) относительно первых производных, получаем

$(8)$

$\begin{align*} &\mathbf{\dot x} = \mathbf v \ & \mathbf{\dot q} = \frac{1}{2} \, \mathbf B^{-1} \, \mathbf D \, \mathbf \omega \\ &\mathbf{\dot v} = \frac{1}{m} \, \mathbf X \ &\mathbf{\dot\omega} = \mathbf I_c^{-1} \, \left(\mathbf M_c - \mathbf \Omega \, \mathbf I_c \, \mathbf \omega \right) \end{align*}$

систему уравнений движения в форме Коши.
В отсутствие внешних силовых факторов правая часть системы (8) равна нулю, и уравнение движения центра масс интегрируется легко, с учетом начальных условий

$\mathbf x(t) = \mathbf x_0 + \mathbf v_0 \, t$

Вращение гайки описывается системой семи уравнений первого порядка, которые получаем из (8), вводя безразмерные моменты инерции $i_y = \frac{I_y}{I_x}$ и $i_z = \frac{I_z}{I_x}$

$(9)$

$\begin{align*} &\dot\lambda_0 = -\frac{1}{2} \, \left( \lambda_1 \, \omega_x + \lambda_2 \, \omega_y + \lambda_3 \, \omega_z \right) \ &\dot\lambda_1 = \frac{1}{2} \, \left( \lambda_0 \, \omega_x + \lambda_3 \, \omega_y - \lambda_2 \, \omega_z \right) \\ &\dot\lambda_2 = -\frac{1}{2} \, \left( \lambda_3 \, \omega_x - \lambda_0 \, \omega_y - \lambda_1 \, \omega_z \right) \\ &\dot\lambda_3 = \frac{1}{2} \, \left( \lambda_2 \, \omega_x - \lambda_1 \, \omega_y + \lambda_0 \, \omega_z \right) \ &\dot\omega_x = \left(i_y - i_z) \, \omega_y \, \omega_z \ &\dot\omega_y = \frac{i_z - 1}{i_y} \, \omega_x \, \omega_z \ &\dot\omega_z = \frac{1 - i_y}{i_z} \, \omega_x \, \omega_y \end{align*}$

Для численного интегрирования системы (9) зададим начальные условия

$\begin{align*} &\lambda_0(0) = 1, \quad \lambda_1(0) = \lambda_2(0) = \lambda_3(0) = 0 \ &\omega_x(0) = \omega_0, \quad \omega_y(0) = \Delta\omega_y, \quad \omega_z(0) = 0 \end{align*}$

где $\omega_0$ — угловая скорость гайки после схода с резьбы; $\Delta\omega_y$ — начальное возмущение угловой скорости

При значениях параметров $i_y = 2.0, \, i_z = 0.5, \, \omega_0 = 1.0$ , рад/с, $\Delta\omega_y = 1 \cdot 10^{-10}$ , рад/с, движение гайки происходит следующим образом

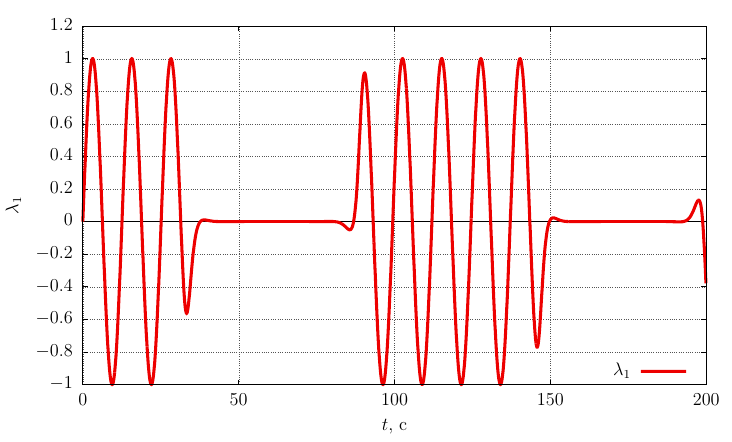
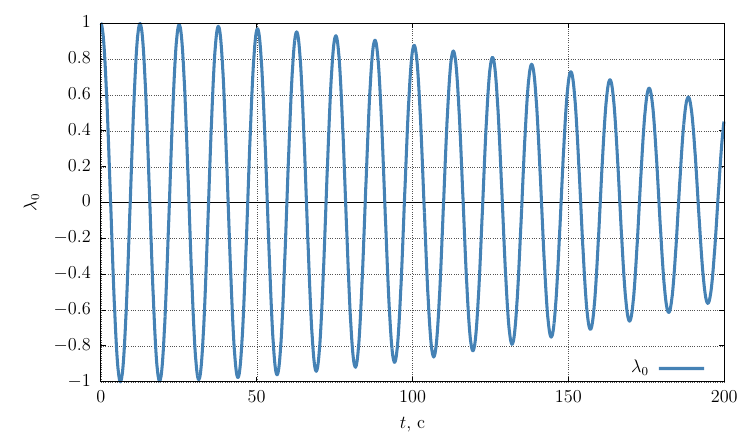
Параметры ориентации Родрига-Гамильтона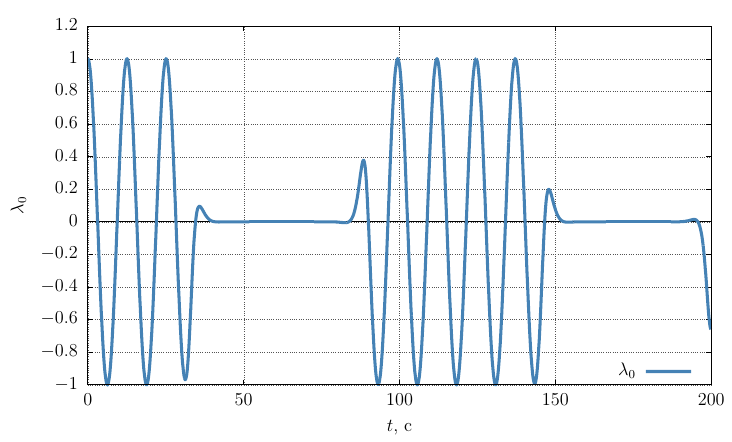

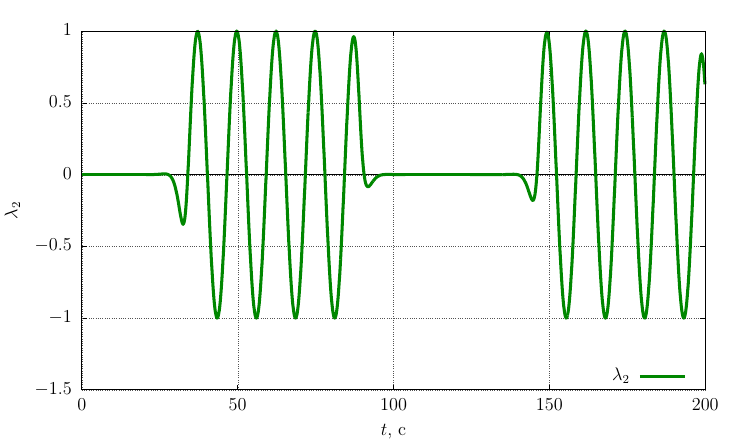
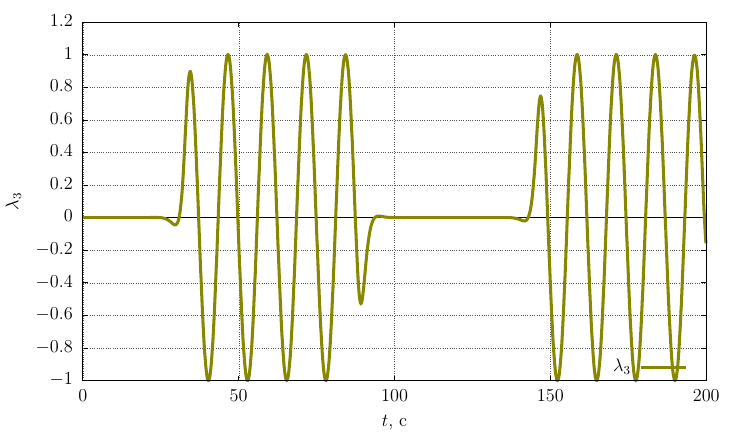
Проекции угловой скорости на собственные оси

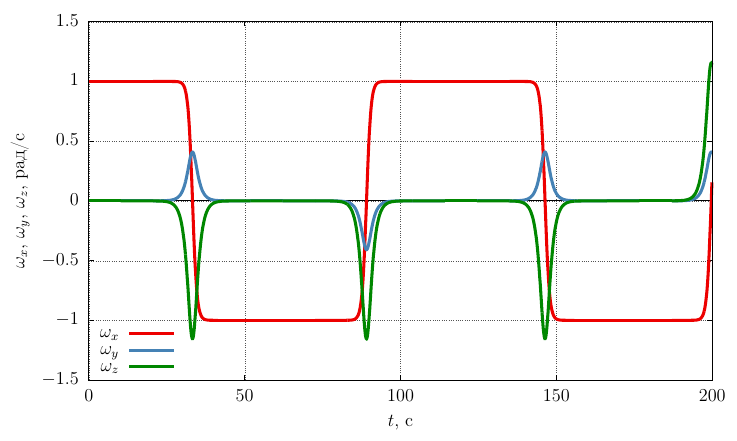
Из графиков видно, что при $I_y > I_x > I_z$ , весьма незначительное возмущение вектора угловой скорости приводит к периодическому лавинообразному изменению ориентации гайки в пространстве.

Сравним полученный результат с движением тела, закрученным вокруг оси с максимальным моментом инерции, то есть положим $I_x > I_y = I_z$ , задав следующие значения параметров $i_y = 0.5, \, i_z = 0.5, \, \omega_0 = 1.0$ , рад/с, $\Delta\omega_y = 1 \cdot 10^{-2}$ , рад/с

Параметры ориентации Родрига-Гамильтона

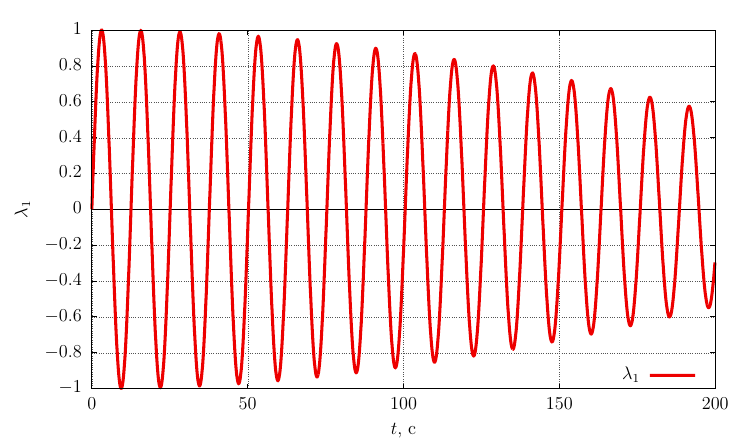
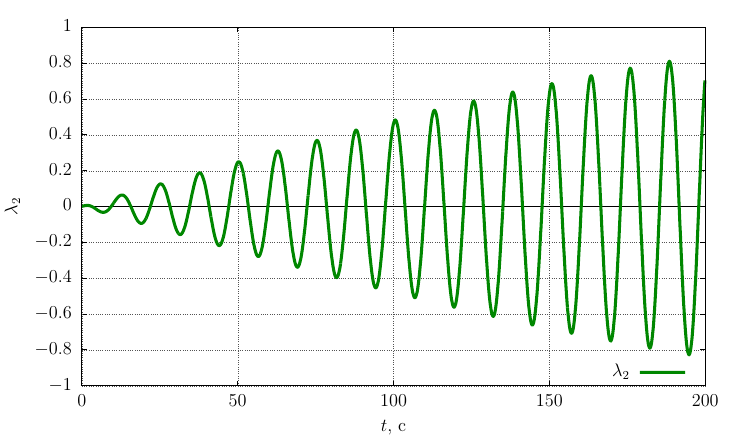
Проекции угловой скорости на собственные оси

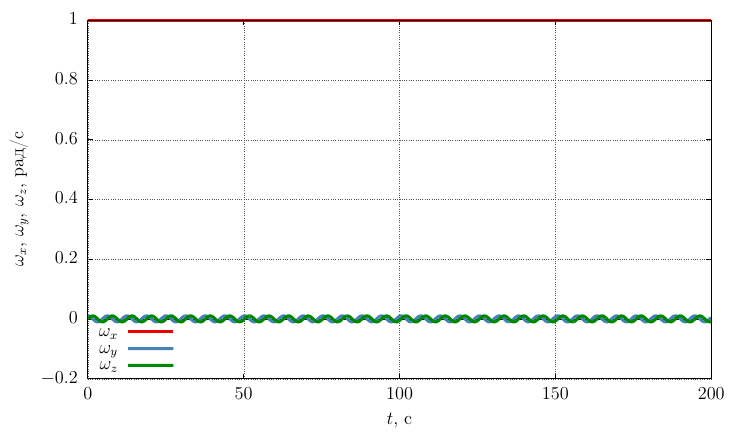
Видно, что при достаточно значительном возмущении угловой скорости движение остается устойчивым вращением вокруг оси $x$ с небольшой прецессией.

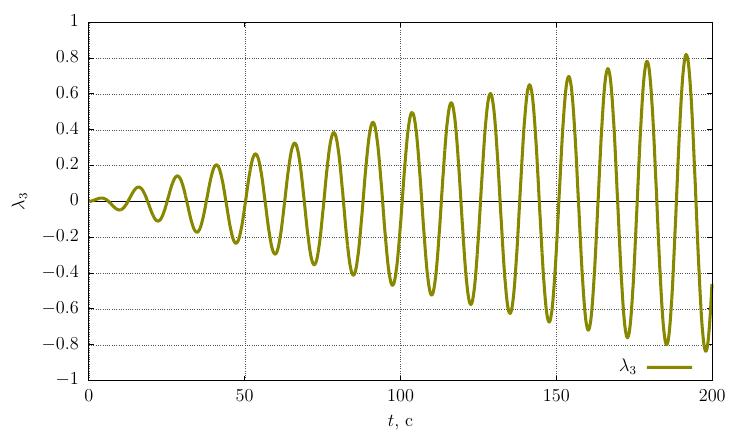
Похожая картина наблюдается для тела, закручиваемого вокруг оси с минимальным моментом инерции ( $I_x < I_y = I_z$ ) $i_y = 1.5, \, i_z = 1.5, \, \omega_0 = 1.0$ , рад/с, $\Delta\omega_y = 1 \cdot 10^{-2}$ , рад/с

Параметры ориентации Родрига-Гамильтона

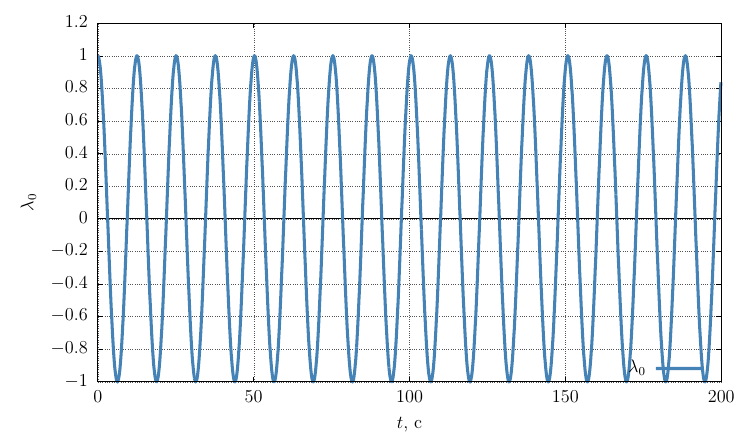
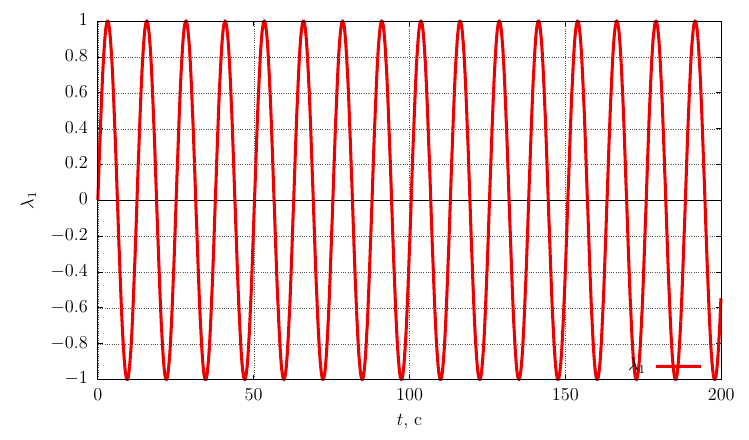
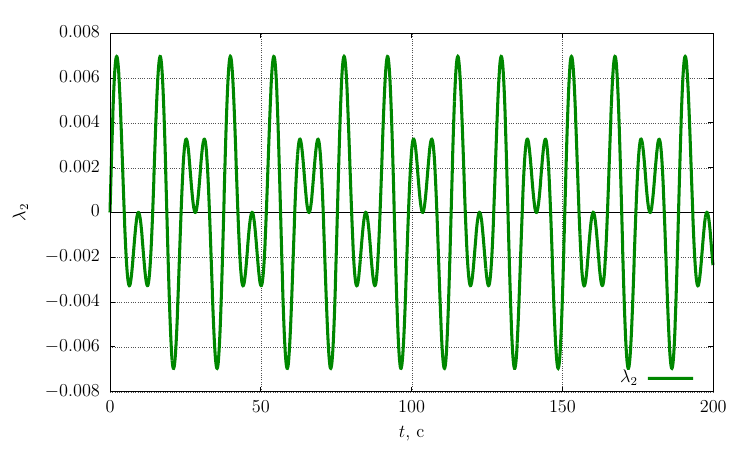
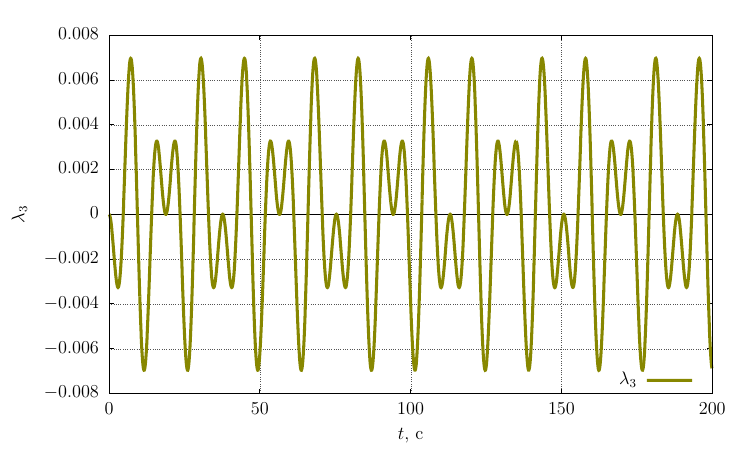
Проекции угловой скорости на собственные оси

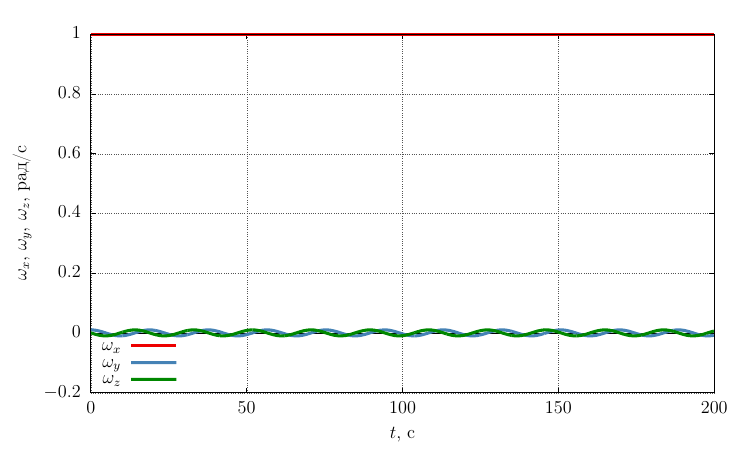
Частота прецессии существенно меньше, чем при закрутке вокруг оси с максимальным моментом инерции, что логично, так как колебания происходят вокруг оси с большим моментом инерции, чем в случае $I_x > I_y = I_z$ .

Все расчеты выполнены автором в СКА Maple 18. Графики построены из лога расчета связкой Kile + LaTeX + gnuplot.

Хотелось бы ещё сделать анимацию, однако опыт автора в этом вопросе крайне мал. Поэтому хотел бы задать вопрос читателям — существует ли ПО (для Linux/Windows), с помощью которого имея набор значений параметров кватерниона ориентации в зависимости от времени сделать анимационный ролик, иллюстрирующий движение тела? Подозреваю, что подобное можно провернуть с Blender 3D, но не уверен.

А пока что, благодарю за внимание!

Продолжение следует…