Магия тензорной алгебры: Часть 12 — Параметры Родрига-Гамильтона в кинематике твердого тела
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
Наконец-то мы подошли к довольно интересной теме — выбору параметров, однозначно определяющих ориентацию твердого тела в пространстве. Исторически наиболее популярными являются углы поворота — они в первую очередь упоминаются в классических учебниках теоретической механики.
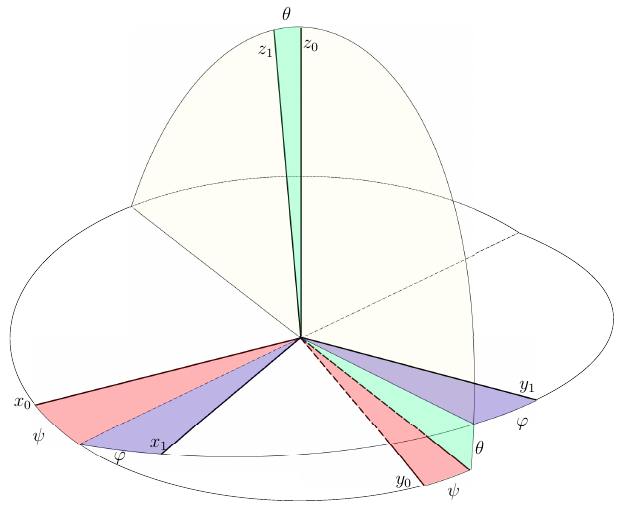
Рис. 1. Углы Эйлера — параметры, знакомые каждому, кто занимался компьютерной графикой и моделированием пространственного движения тел. И каждый, кому они знакомы, знает, насколько проблематичным бывает их использование.
Обычно углы поворота используют совместно с декартовой системой координат, при этом говорят, что связанная система координат может быть совмещена с базовой путем трех последовательных поворотов вокруг её осей. При этом каждый следующий поворот осуществляется вокруг оси, полученной после предыдущего поворота. Кроме того, следующий поворот не должен происходить вокруг оси, относительно которой совершен предыдущий поворот. В связи с этим существует 12 различных комбинаций углов поворота, самыми известными из которых являются углы Эйлера (рисунок 1). Базовую систему координат поворачивают на угол вокруг оси Z (угол прецессии), затем на угол
вокруг оси X (угол нутации), и снова вокруг оси Z на угол
(угол собственного вращения) до совмещения её со связанной системой координат.
Использование углов Эйлера всем хорошо — их число совпадает с числом вращательных степеней свободы твердого тела, а значит они не порождают избыточных уравнений связей. Но, даже не прибегая к громоздким формулам, по рисунку 1, можно догадаться, где кроется проблема.
Рис. 2. Знаменитые кинематические уравнения Эйлера. Я, в своё время, хлебнул с ними долгих и кропотливых отладок
Существует два значения угла нутации, при которых происходит вырождение кинематических уравнений Эйлера (рисунок 2) — и
. Предположим, что угол нутации принял одно из этих значений — тогда угол прецессии и угол собственного вращения описывают поворот вокруг одной и той же оси Z и принципиально неразличимы друг от друга. При использовании кинематических уравнений Эйлера мы получаем ноль в знаменателе и
NaN в фазовых координатах. Приплыли, процедура интегрирования рухнула.
Другой вариант углов поворота — самолетные углы: — рыскание,
— тангаж и
— крен (рисунок 3).
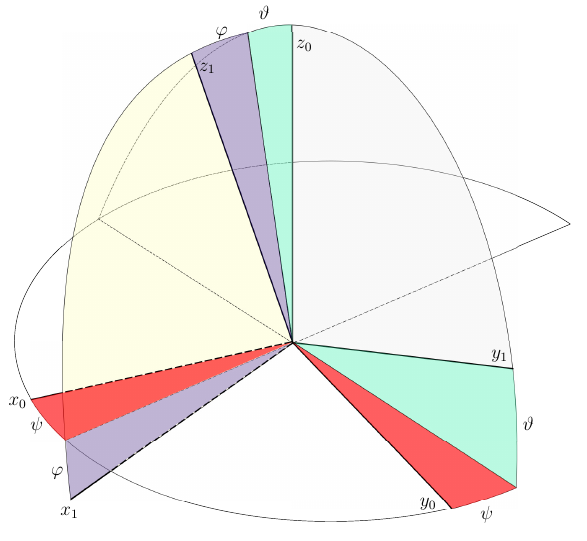
Рис. 3. Самолетные углы — один из практических способов определения ориентации летательного аппарата в пространстве
Данные параметры поворота вырождаются при тангажах , при этом неразличимы становятся крен и рыскание. Матерые симуляторщики знают, как сходит с ума КПП при выходе на крутые тангажи.
Все возможные комбинации углов поворота имеют вырождение. Для моделирования и закладки в алгоритмы систем управления ориентацией область их применения ограничивается критическими значениями параметров. В прошлой статье мы показали, что не подходят и параметры конечного поворота, а использование непосредственно компонентов тензора поворота затрудняется излишне глубокими зависимостями между ними, что порождает высокий порядок системы уравнений движения.
Однако, ещё великий Леонард Эйлер ввел в рассмотрение четыре параметра, которые не имеют вырождения. На его публикацию по этому поводу тогдашний научный мир особого внимания не обратил. Данная идея, независимо от Эйлера была развита Олидом Родригом, а в работах Уильяма Гамильтона получила окончательное теоретическое обоснование. Встречайте —
Кватернионом называют число вида
где называют компонентами кватерниона. Сами числа (1) образуют множество гиперкомплексных чисел
, включающее в себя все действительные
числа и множество комплексных чисел
. Математики эпохи, когда работал Гамильтон, уже знали о комплексных числах и о том, как построенные на их основе методы позволяют решать задачи планиметрии и естественным было желание расширить понятие комплексного числа для применения подобных методов к пространственным задачам. Проблема была в том, что добавление второй мнимой единицы не решало проблемы. Гамильтону пришла в голову мысль, что подобные расширенные комплексные числа могут быть не трех-, а четырехкомпонентными. Работая в этом направлении, в порыве вдохновения на одной из прогулок он вывел правило умножения таких чисел, что окончательно сложило мозаику новорожденной теории.
Так вот, перемножение кватернионов сводится к алгебраической операции перемножения сумм, с той лишь разницей, что требуется определить правила умножения мнимых единиц. Традиционно, каждая из мнимых единиц возведенная в квадрат дает -1
а их попарные произведения хорошо описываются диаграммой
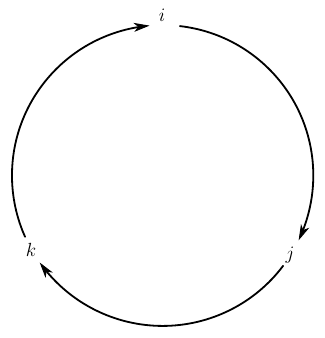
Рис. 4. Диаграмма перемножения мнимых единиц в кватернионе
смысл которой прост — если перемножать пары мнимых единиц в порядке, указанном стрелкой, то получается третья мнимая единица со знаком »+». Если порядок перемножения изменить на противоположный — получится третья мнимая единица со знаком »-». Не напоминает правило векторного перемножения ортов в декартовых координатах? Это оно и есть, то есть мы получаем
Пользуясь этими правилами перемножим два кватерниона
Ого! Не слабо, но мы смело приводим подобные слагаемые
и, ну наверняка вы видите тут до боли знакомые действия над векторами. Пусть у нас будут заданы векторы
тогда каждый кватернион можно представить парой скаляр-вектор
а результат их умножения
Не трудно просто сравнить эту формулу с результатом умножения, которое мы выполнили, при этом считая мнимые единицы ортами декартова базиса. Таким образом, кватернионы включают в себя и векторы трехмерного пространства, и например, кватернионы вида и
, будут скалярами, и их произведение эквивалентно произведению скалярных величин
А кватернионы вида и
называются векторными кватернионами, и их произведение
дает скалярное, со знаком минус, и векторное произведение составляющих их векторов.
Из-за наличия в результате произведения векторного умножения, операция умножения кватернионов не коммутативна
Ну и надо ли говорить, что обнуляя два последних коэффициента у каждого из кватернионов мы получим произведение комплексных чисел? Думаю не стоит, ибо мы не погружаемся в комплексную область, а если и говорим о комплексных числах, то там где это требуется.
Не стану так же говорить о том, что сложение кватернионов и умножение их на число аналогично соответствующим операциям в комплексной области. А вот о чем надо поговорить, так о сопряжении кватерниона
о связанной с ним операции вычисления нормы
и операции вычисления обратного кватерниона
И ещё одно полезное свойство, касающееся сопряжения произведения кватернионов
Кроме того, норма обратного кватерниона — величина обратная норме исходного
Эти операции имеют непосредственное отношение к тому, для чего в наши дни используют гиперкомплексные числа
Теперь посмотрим на вот такой фокус. Пусть — один кватернион, а
— другой кватернион. Докажем небольшую теорему
Преобразование вида
не меняет нормы кватерниона
.
Проверяется это утверждение прямым вычислением
Действительно, норма кватерниона не изменяет при подобном преобразовании. А если кватернион будет векторным кватернионом, то не изменится норма вектора, которым он определяется. То есть описанное преобразование над вектором, не меняет его длины, оно будет ортогональным, или преобразованием поворота! Дело за малым — выяснить, вокруг какой оси и на какой угол происходит поворот, определяемый конкретным кватернионом. Для этого возьмем (нам ведь никто не мешает так сделать) и представим кватернион
в виде
Величину, стоящую в скобках называют вензором (не путать с тензором!) кватерниона. Поупражняемся над его векторной частью
Никто не мешает делать нам эквивалентных преобразований, вот мы и делаем их. Теперь введем замену
На каком основании? Да на том, что сумма квадратов этих величин всегда даст единицу, а если это так, то никто не мешает представить данные величины как синус и косинус некоторого угла. Почему угол делим на два? Нам так хочется, потом это нам пригодится, ведь угол можно взять произвольный. Исходя из введенной замены мы можем переписать кватернион в виде
Заметим, что вектор , введенный нами, является единичным, так как
В довершении позволим себе ещё одно допущение — пусть кватернион будет единичным, то есть
Теперь аккуратно выполним ортогональное преобразование над векторным кватернионом
Теперь умножим результат (2) на обратный кватернион
Для того чтобы не загромождать текст «крокодилами» вычислим отдельно скалярную
и векторную часть
результата преобразования. В конечном итоге, на основании формул (3) и (4), проведя не сложные тригонометрические упрощения, приходим к выводу, что на выходе получается некоторый вектор
Так это же… формула конечного поворота Родрига! Выходит, что преобразование
которое, с учетом того, что для единичного кватерниона операция вычисления обратного кватерниона эквивалентна сопряжению, можно переписать в виде
эквивалентно повороту вектора вокруг оси, задаваемой ортом на угол
. Угол поворота и вектор, вокруг которого происходит вращение можно рассчитать по компонентам кватерниона, исходя из замен, введенных нами выше.
Мы убедились, что единичный кватернион, компоненты которого построены по формулам
определяет конечный поворот. Четыре параметра, которые мы привели и есть те самые параметры Родрига-Гамильтона, которые однозначно определяют ориентацию твердого тела в пространстве и не вырождаются при любых параметрах вращения. Например, если мы обнулим угол поворота, то орт оси вращения так же станет равен нулю. При повороте на любой конечный угол мы всегда можем рассчитать положение оси поворота.
Что же, а за окном тем временем рассвело… План данной статьи был несколько иным, и мы ни слова не сказали о тензорах. Да оно и к лучшему, зато мы теперь имеем четкое представление о том, что за хитрые параметры ориентации будем использовать в дальнейшем.
Благодарю за внимание!
Продолжение следует…
