Квазиньютоновские методы, или когда вторых производных для Атоса слишком много
При первом знакомстве с квазиньютоновскими методами можно удивиться дважды. Во-первых, после беглого взгляда на формулы охватывают сомнения, что это вообще может работать. Однако же они работают. Дальше кажется сомнительным, что они будут работать хорошо. И тем удивительнее видеть то, насколько они превосходят по скорости разнообразные вариации градиентного спуска, причем не на специально построенных задачах, а на самых настоящих, взятых из практики. И если после этого еще остаются сомнения вперемешку с интересом — то нужно разбираться в том, почему вообще работает это нечто.
Ранее уже рассматривалось происхождение и основные идеи, которые приводят в движение градиентные методы, включая метод Ньютона. А именно, мы опирались на ту информацию о поведении функции в окрестности текущего положения, которую дает нам незамысловатый математический анализ. Как минимум предполагалось, что информация о первых производных нам доступна. Что делать, если это все, что нам доступно? Градиентный спуск — наш приговор? Конечно да, если только вдруг не вспомнить, что мы имеем дело с процессом, в ходе которого целевая функция как следует прошаривается. И раз так, что почему бы нам не использовать накопленную информацию о поведении функции для того, чтобы сделать наше блуждание по ее поверхности чуть менее слепым?
Идея использования информации о пройденном пути лежит в основе большинства способов ускорения методов спуска. В этой статье рассматривается один из самых эффективных, хотя и не самый дешевый, способ учета такого рода информации, приводящий к идее квазиньютоновских методов.
Для того, чтобы понять откуда растут ноги у квазиньютоновских методов и откуда вообще пошло такое название, нам снова придется вернуться к методу минимизации, основанному на непосредственном решении уравнения стационарной точки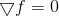 
. Ровно также, как рассмотрение метода Ньютона, примененного к решению данного уравнения, привело нас к одноименному методу оптимизации (который, в отличие от своего прародителя, имеет глобальную область сходимости), мы можем рассчитывать, что рассмотрение иных методов решения систем нелинейных уравнений будет плодотворным в плане идей для построения других методов оптимизации.
Методы секущих
Напомню, что метод Ньютона для решения системы уравнений 
, основан на замене в окрестности некоторой близкой к решению точки 
функции 
ее линейной аппроксимацией 
, где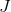 
— линейный оператор, который в случае, когда является вектором и имеет частные производные по каждой переменной, совпадает с матрицей Якоби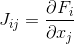 
. Далее решается уравнение 
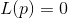и точка 
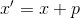принимается в качестве нового приближения к искомому решению. Это просто и это работает.
Но что делать, если матрицу Якоби мы по каким-либо причинам вычислить не можем? Первое, что в данном случае приходит в голову — если мы не можем вычислить частные производные аналитически, то вполне можем получить для них численное приближение. Самым простым (хотя и далеко не единственным) вариантом такого приближения может служить формула правых конечных разностей: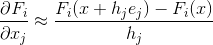 
, где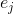 
— j-й базисный вектор. Матрицу, составленную из таких приближений, будем обозначать 
. Анализу того, насколько заме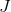на на в методе Ньютона влияет его сходимость, посвящено достаточно большое количество работ, но нас в данном случае интересует другой аспект. А именно, такое приближение требует вычисления функции в N дополнительных точках, и, кроме того, функция 
в этих точках интерполирует функцию , т.е.
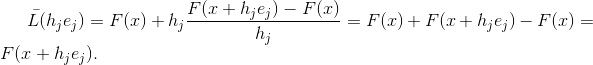
Не каждая аппроксимация матрицы Якоби обладает таким свойством, но каждая матрица аффинной функции, обладающей таким свойством, является аппроксимацией матрицы Якоби. Действительно, если 
и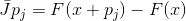 
, то при 
. Данное свойство, а именно — свойство интерполирования, дает нам конструктивный способ обобщить метода Ньютона.
Пусть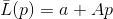 
— функция, удовлетворяющая требованию 
для некоторой системы линейно независимых векторов 
. Тогда такая функция называется секущей функции , а определяющее ее уравнение — уравнением секущей. Если при этом система векторов полна (то есть их ровно N и они все еще линейно независимы), и, кроме того, система векторов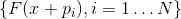 
линейно независима, то 
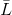определяется однозначно.
Любой метод, построенный на основе локальной замены уравнения уравнением вида 
, где 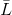удовлетворяет уравнению секущих, называют методом секущих.
Возникает справедливый вопрос о том, как наиболее рациональным способом построить секущую для функции . Кажется очевидным следующий ход рассуждений: пусть в точке x уже построена аффинная модель, которая интерполирует заданную функцию в точках 
. Решение уравнения дает нам новую точку 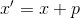. Тогда для построения аффинной модели в точке 
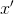разумнее всего выбрать точки интерполяции так, что в них значение уже известно — то есть взять их из множества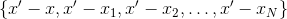 
. Возможны разные варианты того, какие именно точки выбирать из множества ранее использованных. Например, можно взять в качестве точек интерполяции такие, в которых 
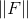имеет наименьшее значение, либо просто первые 
точек. В любом случае, кажется очевидным, что 
следует включать в множество точек интерполяции для новой аффинной модели. Таким образом, за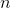 
шагов итерационного процесса в нашем множестве может оказаться до 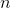смещений, построенных по ранее пройденным точкам. Если процесс построен таким образом, что новая аффинная модель использует не более 
предыдущих значений, то такой процесс называют p-точечным методом секущих.
На первый взгляд может показаться, что наилучшим кандидатом на роль замены метода Ньютона выступает N-точечный метод секущих, поскольку в нем максимально используется информация, которую мы получаем в процессе решения, и при этом минимизируется количество дополнительных вычислений — ведь мы используем значение функции в последних N пройденных точках. К сожалению, это не так. Все дело в том, что система векторов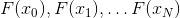 
упорно отказывается быть линейно независимой при достаточно большом N. Кроме того, даже если это условие оказывается выполненным и соответствующая аффинная модель все-таки существует, то вот шанс, что направления 
также окажутся линейно независимы, оказывается еще меньше. А это влечет за собой то, что аффинная модель хоть и существует, но является вырожденной и практически непригодной.
Вообще, самым устойчивым оказывается 2-х точечный метод секущих. То есть метод, в котором на каждой итерации нам придется вычислять дополнительно N-1 значений функции. Это явно не подходит для наших практических целей.
Тогда вопрос —, а к чему все это было?
Квазиньютоновские методы решения уравнений
Выход из положения прост, хотя и не очевиден. Если у нас нет технической возможности на основании уже вычисленных значений однозначно определить аффинную модель, удовлетворяющую уравнению секущих — то и не надо. Возьмем уравнение секущих за основу, но будем требовать, чтобы оно выполнялось только для некоторой неполной системы векторов 
. Иными словами, мы будем требовать выполнение условия интерполяции только для достаточно малого количества известных значений. Разумеется, в этом случае мы уже не можем гарантировать, что используемая в такой модели матрица будет стремиться к матрице Якоби, однако это нам и не потребуется. Добавив к этому, что аффинная модель должна интерполировать функцию в текущей точке, то есть 
, мы получаем следующую формулировку метода секущих:
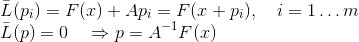
Бройден был первым, кто рассмотрел методы такого вида при m=1, назвав их квазиньютоновскими. Понятно, что условие секущих в данном случае позволяет однозначно идентифицировать матрицу 
только если наложить на нее дополнительные условия, и каждое такое дополнительное условие порождает отдельный метод. Сам Бройден рассуждал следующим образом:
поскольку движение в направлении от точки 
к точке 
не дает нам никакой дополнительной информации о том, как изменяется функция в отличных от направлениях, то воздействие новой аффинной функции на вектор 
должно отличаться от воздействия старой функции на тот же вектор тем меньше, чем больше отличается от . В крайнем случае, когда ортогонален , поведение новой функции вообще не должно отличаться от поведения старой.
Идея Бройдена гениальна в своей простоте. Действительно, если мы не имеем новой информации о поведении функции, то лучшее, что мы можем сделать — постараться не профукать старую. Тогда дополнительное условие
для всех , таких, что 
позволяет однозначно определить матрицу нового преобразования — она получается добавлением к старой матрице поправки ранга 1.
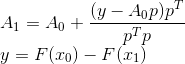
Однако, не смотря на простоту и логичность сделанных Бройденом умозаключений, они не дают той точки опоры, которая могла бы послужить основой для построения других аналогичных методов. К счастью, существует более формальное выражение его идеи. А именно, построенная таким образом матрица 
оказывается решением следующей задачи:
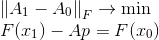
Ограничение задачи представляет собой ни что иное, как уравнение секущей, а условие минимизации отражает наше желание сохранить как можно больше информации, содержащейся в матрице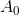 
. Мерой расхождения между матрицами в данном случае выступает норма Фробениуса, в которой поставленная задачи имеет однозначное решение. Эта формулировка уже вполне может послужить отправной точкой для построения других методов. А именно, мы можем изменить как меру, посредством которой оцениваем вносимые изменения, так и ужесточить условия, накладываемые на матрицу. В общем, с такой формулировкой метода уже можно работать.
Квазиньютоновские методы оптимизации
Поняв основную идею, мы наконец можем вернуться к задачам оптимизации и заметить, что применение формулы Бройдена для пересчета аффинной модели, не слишком удачно ложится на нашу задачу. В самом деле, первая производная от функции-градиента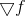 
есть ни что иное, как матрица Гессе, которая по построению является симметричной. В то же время, обновление по правилу Бройдена приводит к несимметричной матрице даже если 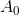была симметричной. Это не значит, что метод Бройдена не может быть применен для решения уравнения стационарной точки, но на основании такого правила обновления мы вряд ли сможем построить хорошие методы оптимизации. Вообще достаточно очевидно, что квазиньютоновский метод должен работать тем лучше, чем точнее система условий задачи описывает специфику конкретной матрицы Якоби.
Для исправления указанного недостатка добавим дополнительное ограничение к бройденовской задаче минимизации, явно потребовав, чтобы новая матрица была симметричной наряду со старой:
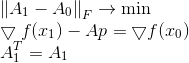
Решением данной задачи является
Здесь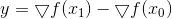 
, а формула пересчета матрицы носит имя своих создателей — Пауэлла, Шанно и Бройдена (PSB). Получаемая в результате матрица симметрична, но явно не является положительно определенной, если только вдруг 
не окажется коллинеарным . А мы видели, что положительная определенность является крайне желательным в методах оптимизации.
Опять скорректируем условие задачи, использовав на этот раз в качестве меры расхождения матриц масштабированную норму Фробениуса.
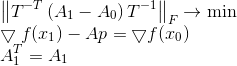
Происхождение такой постановки вопроса — отдельная большая тема, однако интересно, что если матрица T такова, что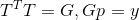 
(то есть G также является матрицей аффинного преобразования, удовлетворяющего уравнению секущих для направления p), то решение данной задачи оказывается независимым от выбора T и приводит к формуле обновления
известной как формула Давидона-Флетчера-Пауэлла. Данный способ обновления неплохо зарекомендовал себя на практике, поскольку обладает следующим свойством:
если 
и 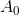положительно определена, то также положительно определена.
Отмечу вдогонку, что если первое условие не выполнено, то вообще не существует аффинной функции с положительно определенной матрицей, которая удовлетворяет уравнению секущей.
Если в задаче, приводящей к DFP-методу, взять в качестве меры расхождения аффинных моделей расстояние не между самими матрицами, а между обратными к ним, то получим задачу вида
Ее решение — широко известная формула, открытая почти одновременно Бройденом, Флетчером, Гольдфарбом и Шанно (BFGS).
На сегодняшний день считается, что пересчет по этой формуле наиболее эффективен с вычислительной точки зрения и при этом наименее склонен к вырождению матрицы при большом количестве итераций. Данная формула при тех же условиях, что и DFP приводит к сохранению свойства положительной определенности.
Все описанные методы обновления матрицы предполагают внесение поправки ранга 2. Это позволяет легко и непринужденно обратить матрицу , используя формулу Шермана-Моррисона и значение 
.
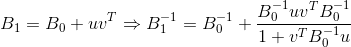
при условии, что знаменатель формулы отличен от нуля. Конкретные формулы для обновления обратных матриц перечисленных методов я приводить не буду, поскольку их легко найти или вывести самостоятельно. Единственное, что в данном случае следует отметить — варианты методов с обновлением обратной матрицы обычно намного менее устойчивы (то есть сильнее страдают от ошибок округления), чем те, что предполагают обновление исходной матрицы. Наиболее эффективно обновлять не саму матрицу, а ее разложение Холецкого (если, конечно, такое разложение имеет место), поскольку такой вариант реализации обладает большей численной устойчивостью и вдобавок минимизирует расходы на решение уравнения, определяющего направление движения.
Осталось рассмотреть вопрос о том, как должна выглядеть самая первая матрица в квазиньютоновском процессе. Здесь все очевидно — чем она ближе к матрице Гессе или к ее скорректированному варианту, если гессиан вдруг не окажется положительно определенным, тем будет лучше с точки зрения сходимости. Однако в принципе нам может подойти любая положительно определенная матрица. Самый простой вариант такой матрицы — единичная, и тогда первая итерация совпадает с итерацией градиентного спуска. Флетчером и Пауэллом было показано (естественно, для DFP-метода), что в случае минимизации квадратичной функции в независимости от того, какая (положительно определенная) матрица будет использована в качестве начальной DFP-итерации приведут к решению ровно за N итераций, где N — размерность задачи, причем квазиньютоновская матрица совпадет с матрицей Гессе в точке минимума. В общем нелинейном случае такого счастья мы, само собой, не дождемся, однако это по крайней мере дает повод не слишком переживать на счет неудачного выбора начальной матрицы.
Заключение
Описанный подход к построению квазиньютоновских методов не является единственно возможным. Как минимум, первооткрыватели описанных квазиньютоновских методов и многие последующие исследователи приходили к тем же формулам исходя из совершенно иных соображений. Однако интересно, что как только появлялся некоторый квазиньютоновский метод, то в независимости от способа его получения спустя довольно короткое время выяснялось, что он является решением некоторой весьма легко трактуемой задачи оптимизации. На мой взгляд замечательно, что оказывается возможным подвести некий общий знаменатель под такие разнообразные методы, поскольку это дает почву для построения других, лучше учитывающих специфику конкретной задачи методов. В частности, существуют квазиньютоновские методы, рассчитанные на обновление разреженных матриц, методы, в которых изменению подвергается как можно меньшее число элементов, и многие другие — была бы фантазия.
Следует также отметить, что методы переменной метрики, несмотря на свое название, не всегда приводят к построению матриц, которые собственно метриками являются, хотя и делают это каждый раз, когда это вообще возможно. Это обычно не составляет большой проблемы, однако желающие обезопасить себя от возможного конфуза вполне могут прибегнуть к тем же ухищрениям, которые делались для преодоления аналогичной проблемы у метода Ньютона — например, путем смены направления или применения схемы Левенберга-Марквардта. Правда, в этом случае снова приобретут актуальность вопросы выбора формы доверительного региона, но тут уж придется выбирать меньшее из зол.
Теоретически определить, какой из огромного количества возможных квазиньютоновских методов окажется наиболее эффективным по отношению к некоторому классу задач практически невозможно. Обычно при формулировании метода ограничиваются тем, что показывают его эффективность при минимизации квадратичной функции (к слову, метод считается эффективным, если приводит к точному решению за N итераций, то есть не медленнее, чем прямые методы решения СЛАУ). В более редких случаях можно найти исследования порядка сходимости метода (который обычно сверхлинейный, то есть существенно лучше того, что нам дает градиентный спуск), устойчивости и других представляющих интерес характеристик. Но в целом, единственный разумный критерий, позволяющий судить об эффективности того или иного метода для конкретного класса задач — практика. Так что лопаты в руки — и успехов в применении.
