Квантовые вычисления: отжиг с выключателями и прочее веселье
В предыдущей статье мы начали рассказ о квантовых вычислениях и сравнили их с обычными. Сегодня мы погрузимся глубже в их технические особенности и расскажем, как это используется на благо человечества.

Квантовый параллелизм
Согласно законам квантовой механики, частица может находиться во всех своих состояниях одновременно. Это состояние кубита называется суперпозиция. В суперпозиции амплитуды базисных состояний принимают ненулевые значения — a|0⟩ + b|1⟩ и при этом сохраняется требование нормировки.
Квантовая частица может находиться в суперпозиции только до момента измерения. После измерения она коллапсирует в одно из своих базисных состояний — 0 или 1. Если мы имеем регистр кубитов, которые находятся в суперпозиции, то состояние самого регистра можно определить следующим образом:
(a0×0⟩ + b0×1⟩)(a1×0⟩ + b1×1⟩)…(an|0⟩ + bn|1⟩) =
a0×a1×…×an|00…0⟩ + a0×a1×…×bn|00…1⟩ +…+ b0×b1×…×bn|11…1⟩
Важно понимать, что множители, которые стоят перед состояниями, — это не вероятность. Иначе мы бы получили классическую систему с ограничением — неизвестно, в каком именно состоянии она находится. А квантовый бит находится в обоих состояниях одновременно. Мы имеем возможность обработки сразу всех 2n возможных комбинаций!
Для того чтобы перевести кубит в состояние суперпозиции, нужно применить к нему специальное преобразование — гейт Адамара. Еще одно применение гейта Адамара вернет кубит в одно из базисных состояний. Так выглядит матрица гейта Адамара и пример его применения:
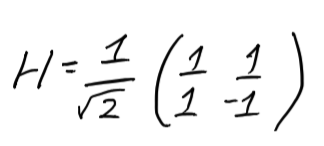
H×|0⟩ = H×(1×0⟩ + 0×1⟩) = 1/sqr (2)|0⟩ + 1/sqr (2)|1⟩
H×(1/sqr (2)|0⟩ + 1/sqr (2)|1⟩) = 1×0⟩ + 0×1⟩ = |0⟩
Интересно действие двухкубитного гейта CNOT при контролирующем кубите в суперпозиции — CNOT запутывает кубиты. Запутанное состояние — это явление, при котором кубиты нельзя рассматривать по отдельности, так как их состояние теперь общее.
Приведем пример. Допустим, у нас есть регистр из двух кубитов в начальном состоянии — в базисном состоянии |0⟩). Применим гейт Адамара к первому кубиту — получим следующее состояние регистра:
H×I×|00⟩= H×(1×0⟩ + 0×1⟩) × I×(1×0⟩ + 0×1⟩) = (1/sqr (2)|0⟩ + 1/sqr (2)|1⟩) × (1×0⟩ + 0×1⟩) =
1/sqr (2)|00⟩ + 1/sqr (2)|10⟩
Первый и второй кубиты в этом регистре независимы друг от друга. Второй кубит до сих пор в состоянии |0⟩ и если мы его измерим, то все равно не получим информации о состоянии первого — тот может быть как в состоянии 0, так и в состоянии 1. Применим двухкубитный гейт CNOT:
CNot × (1/sqr (2)|00⟩ + 1/sqr (2)|10⟩) = CNot × (1/sqr (2)|00⟩ + 0×01⟩ + 1/sqr (2)|10⟩ + 0×11⟩) =
1/sqr (2)|00⟩ + 0×01⟩ + 0×10⟩ + 1/sqr (2)|11⟩ = 1/sqr (2)|00⟩ + 1/sqr (2)|11⟩
Теперь кубиты находятся в запутанном состоянии, и измерение любого из них заставит немедленно коллапсировать другой! Состояние регистра показывает, что оба кубита находятся в одинаковом состоянии — 0 или 1. Так что измерив один, мы точно узнаем состояние другого.
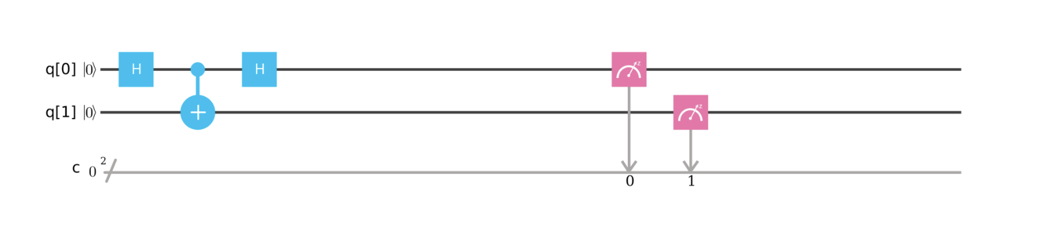
После того, как мы запутали кубиты, нельзя просто так свернуть один из них в базисное состояние — их нужно сначала распутать. Попробуйте самостоятельно создать данную схему на квантовом редакторе IBM и оцените результат:
Коллапс и количество получаемой информации
Производя вычисления над квантовым регистром из n кубитов, мы имеем возможность одновременно обрабатывать все 2n возможных состояния. Однако при измерении каждый кубит коллапсирует в одно из своих базисных состояний, а значит — после измерения результата у нас нет возможности получить больше информации, чем в классическом случае — мы получим только одно из возможных состояний с соответствующей вероятностью.
Квантовые алгоритмы учитывают это свойство и предлагают множество подходов для решения конкретного класса задач. Например, в одном из подходов проводится множество такого типа преобразований, которые увеличивают амплитуду искомого решения и уменьшают амплитуды остальных.
Алгоритм Гровера
Алгоритм, представляющий множество таких преобразований, называется алгоритмом Гровера. Он позволяет квадратично ускорить поиск в неструктурированной БД. Обычно сложность поиска в неструктурированном наборе данных равна O (n), то есть в худшем случае нам необходимо просмотреть все записи. Квантовый алгоритм позволяет решить эту задачу за O (√n).
Например, у нас есть 40 бит и нам нужно найти одну из всех возможных комбинаций, удовлетворяющую некоторому условию. В классическом случае нам понадобится обработать порядка 1 000 000 000 000 разных комбинаций. Квантовый алгоритм позволит получить результат за 1 000 000.
Рассмотрим пример. У нас имеется регистр из n кубитов, находящихся в суперпозиции. Таким образом, у нас есть 2n всех возможных состояний, и амплитуда каждого равна 1/√2n (именно при таком значении сумма квадратов модулей будет равна 1). Изобразим это в виде диаграммы:

Также у нас есть один дополнительный кубит, который мы будем называть функциональным, и функция-оракул. Оракул переводит функциональный кубит из базисного состояния |0⟩ в состояние |1⟩ ровно на том наборе, который мы ищем.
Чтобы при измерении получить именно то состояние, которое соответствует функции-оракулу, мы проделываем следующие действия:
- Изменяем знак амплитуды искомого значения на отрицательный. Для этого переводим функциональный кубит в состояние |1⟩ на всех наборах, далее применяем к нему гейт Адамара и затем функцию-оракул ко всему регистру. После этого действия картина будет выглядеть так:

Пунктирной линией на рисунках отмечено среднее значение амплитуды. После того, как знак у целевой амплитуды изменился, значение среднего опустилось ниже.
- Так как мы обрабатываем все состояния одинаково, то не можем изменить какую-то одну амплитуду. Но можем сделать инверсию относительно среднего — отобразить значение амплитуды, взяв за ось значение среднего:

- Как мы видим, значение искомой амплитуды выросло относительно остальных. По итогам выполнения этого набор действий порядка Pi×0,25×√2n раз, искомая амплитуда будет почти равна единице.
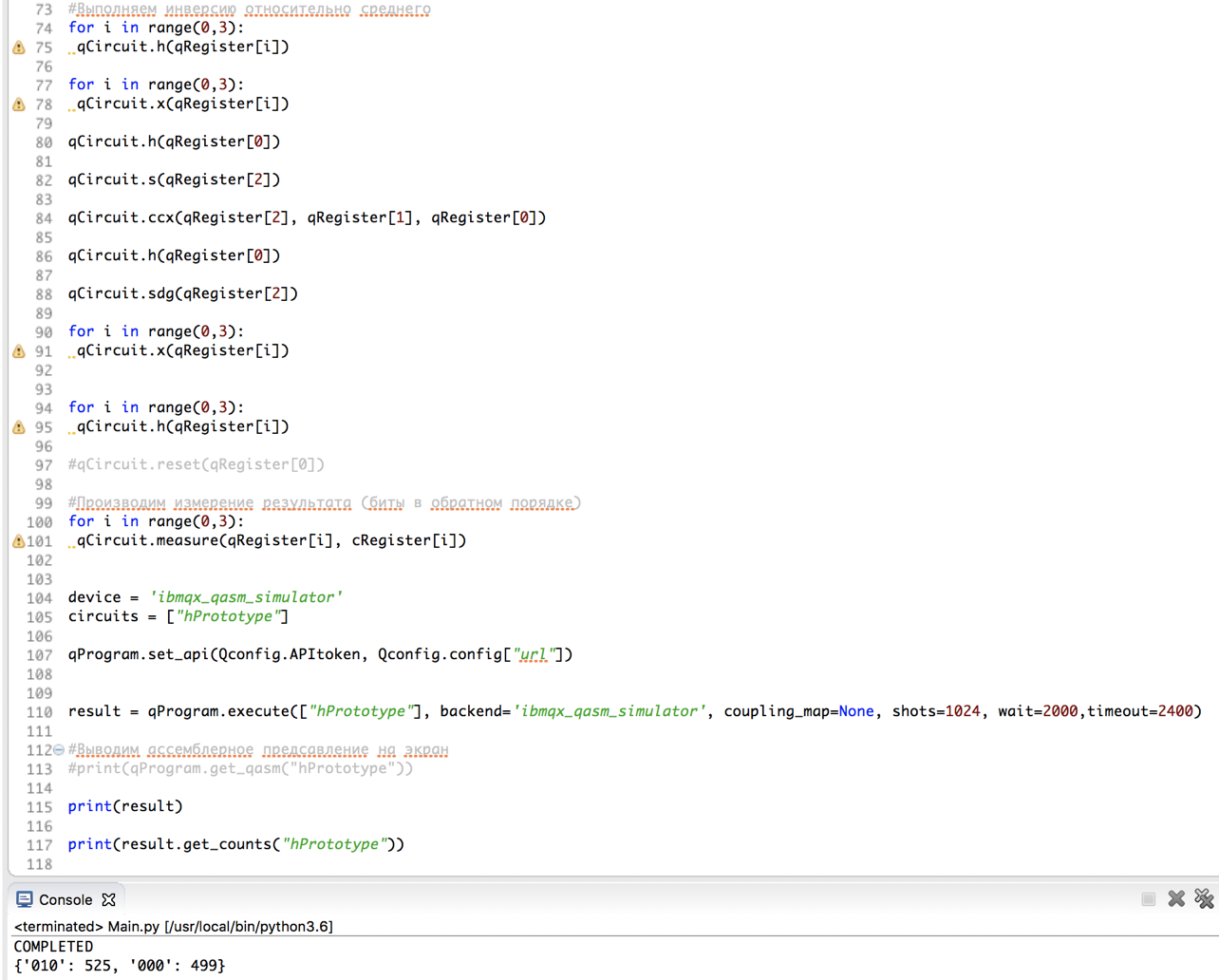
Представим, например, что нам нужно найти число в диапазоне от 0 до 7, которое после циклического битового сдвига влево даст число, меньшее 2. На классическом вычислителе данный класс задач решается только перебором. Нам необходимо было бы вычислить нашу функцию (битовый сдвиг) на всех аргументах и затем к каждому результату применять условие. Квантовый алгоритм позволяет сделать это моментально.
Квантовая оптимизация
Все рассмотренные ранее алгоритмы и приемы справедливы для так называемого универсального квантового компьютера — вычислителя, способного производить элементарные преобразования и фактически решать любую задачу (в простейшем случае моделируя классический алгоритм).
Но существует целый пласт математических задач, в которых как таковые вычисления не требуются, а необходимо найти такую комбинацию аргументов, на которой определённого вида функция примет минимальное значение. Этот класс задач — задачи оптимизации — подробнее будет разобран далее.
Квантовый отжиг
Отжиг — процесс постепенного остывания вещества, при котором молекулы на фоне замедления теплового движения собираются в наиболее энергетически выгодные конфигурации. Термин «отжиг» пришёл из металлургии. В более энергетически выгодном состоянии металл становится одновременно твёрже и прочней: требуется большее внешнее воздействие, большая механическая работа над куском металла, чтобы нарушить выгодную конфигурацию молекул, «приподнять» эту конфигурацию над самым дном энергетической ямы.
Подобно классическому отжигу, при медленном включении межчастичного взаимодействия квантовая система «ищет» энергетически наиболее выгодную конфигурацию посредством эффектов квантовой механики. Квантовые вычисления на основе квантового отжига позволяют решать определенные проблемы, которые затруднительно решать с использованием классических компьютеров.
Рассмотрим математическую задачу, известную под названием «игра с выключателями света». Ее цель — нахождение лучших конфигураций включения и выключения для множества переключателей. Вот как это выглядит графически:
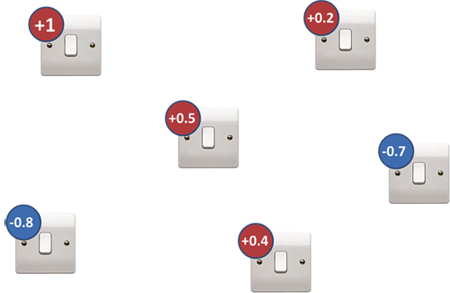
Представим, что у каждого переключателя есть вес, который мы не можем изменить. Мы можем включать (ON) или выключать (OFF) каждый переключатель. ON обозначает умножение на 1, а OFF — на -1. Затем мы складываем все веса переключателей, умноженные на их значения ON / OFF. Цель игры — установить переключатели для получения самого низкого значения суммы. Вес i-го выключателя обозначим через hi, а состояние переключателя через si.
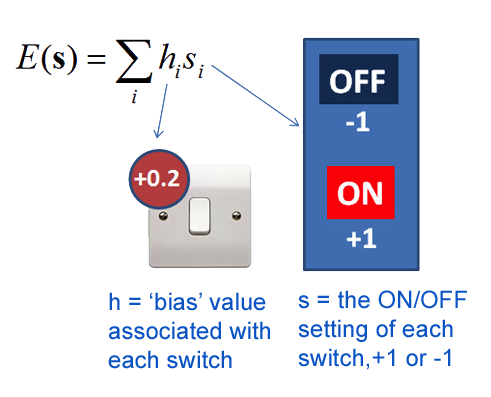
В зависимости от того, какие переключатели установлены на ON или OFF, мы получим разные итоговые суммы. Найти минимальную сумму будет легко, потому что есть простое правило для гарантированного минимума:
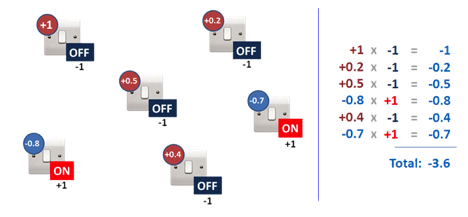
Если мы установим все переключатели с положительными показателями в положение OFF, а все переключатели с отрицательными показателями — в положение ON, то в сумме получим самое низкое общее значение.
Теперь усложним задачу: добавим новый вес J. Он будет изменяться в соответствии с состояниями ON/OFF соседних переключателей. А затем включен в итоговую сумму, которую мы получили ранее.

Теперь гораздо сложнее решить, должен ли выключатель быть включен или выключен, потому что его соседи влияют на него. Даже в простом примере с двумя переключателями мы не можем просто устанавливать параметр ON/OFF в положение, противоположное знаку собственного веса переключателей. Со сложной сетью выключателей задача становится практически нерешаемой.
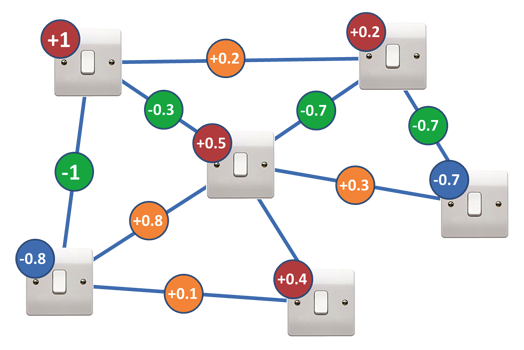
С помощью нескольких переключателей мы можем просто попробовать каждую комбинацию ON и OFF, есть только четыре возможности: [ON ON], [ON OFF], [OFF ON] или [OFF OFF]. Но по мере того, как мы добавляем все больше и больше переключателей, количество возможных способов установки переключателей растет экспоненциально:

Как поможет квантовая механика? Мы начинаем с системы в ее квантовой суперпозиции, затем привлекаем квантовый компьютер (DWave), который, используя квантовую оптимизацию, находит для выключателей то состояние, в котором значение суммы будет самым низким.
«Задача инкассатора»
Давайте сформулируем тестовую задачу и попробуем ее решить с помощью квантового компьютера DWave. Задача звучит так — у банка есть служба инкассации и множество банкоматов в городе, откуда нужно забрать деньги. Чем короче маршрут, тем меньше шансов попасть в неприятную ситуацию. Соответственно нам необходимо найти оптимальный маршрут во взвешенном направленном графе с N вершинами. Эта задача больше известна под именем «Задача коммивояжера» и не имеет лучшего варианта решения, чем полный перебор.
Для того, чтобы решить эту задачу, нужно сначала понять, каким образом производится решение задач на DWave. Сначала мы должны разработать входной файл конфигурации. Он имеет следующий формат:
c
c This is a sample .qubo file
c with 4 nodes and 6 couplers
c
p qubo 0 4 4 6
c — 0 0 3.4
1 1 4.5
2 2 2.1
3 3 -2.4
c — 0 1 2.2
0 2 3.4
1 2 4.5
0 3 -2
0 2 3.4
1 2 4.5
0 3 -2
1 3 4.5678
2 3 -3.22
Через «с» обозначены строки с комментариями, далее мы задаем параметры программы в строке, начинающейся с символа «p». В этой строке мы задаем топологию (пока всегда 0), количество кубитов (в терминах игры со светом это «выключатели») и связей между парами (весы «J»). Далее идет блок с описанием весов каждого кубита. В этом блоке первые два числа должны быть одинаковыми, и они соответствуют номеру кубита. Следующий блок — блок весов связей между парами. Номер первого кубита должен быть всегда меньше второго.
Итак, разобравшись с форматом, приступим к решению нашей задачи.
Сначала мы выделим понятие шага пути — это набор всех возможных вершин графа, в которых мы можем находиться в текущий момент времени. Каждая вершина представлена кубитом. И таких шагов у нас будет N, где N — количество вершин в нашем графе.
Предположим, у нас всего 4 вершины, на каждом шаге мы можем находиться в одной из 4 вершин, соответственно весь набор кубитов разбивается на блоки по 4 кубита. В нашем случае из 4 вершин, нам нужен будет регистр из 16 кубитов, пронумеруем их — a0…a16. Соответственно, в первом блоке будут кубиты с номерами a0…a3 — они соответствуют нахождению в одной из вершин на первом шаге.
Теперь надо расставить веса кубитов и их связей внутри одного блока таким образом, чтобы только один кубит в каждом блоке в конечном решении оказался в состоянии 1, а остальные в 0. Это связано с тем, что в конечном итоге мы можем находиться только в одной из вершин на каждом шаге. Сделать это довольно просто — мы выставим вес каждого кубита в -1, а связи между ними в 2. Действительно, если мы посмотрим на формулу Σhisi + ΣJijsisj, то увидим, что минимальна она будет, если второе слагаемое будет равно нулю. А это произойдет только в двух случаях — если все кубиты равны 0 или если один любой находится в 1, а остальные в 0. Но при этом первое слагаемое даст минимум во втором случае.
Итак, мы выставляем таким образом веса на всех шагах (блоках из вершин) нашего пути. Теперь, если мы пошлем нашу программу на исполнение, нам придёт ответ вида (0001 0100 1000 1000). Для удобства мы разделили их на блоки по 4 кубита пробелами. Мы видим, что в каждом блоке только одна единичка, и ее номер в блоке соответствует номеру вершины. В нашем решении есть блоки с одинаковым номером вершины — 1000. Нам нужно исключить такие варианты решения, т.к. мы не можем возвращаться в уже пройденные вершины. Для того, чтобы сделать это, мы будем рассматривать новые блоки — объединяющие одну и ту же вершину на разных шагах.
Рассмотрим блок a0, a4, a8, a12. Эти кубиты соответствуют нахождению в первой вершине на соответствующем шаге. Аналогично предыдущему пункту, только один из них должен быть равен единице — тогда мы окажемся в первой вершине только один раз за весь путь. Расставляем веса связей для всех таких блоков и отправляем программу на исполнение. Получаем ответ вида (0001 0100 1000 0001 0010). Отлично, мы уже получили путь, соответствующий определению, теперь нужно найти оптимальный путь согласно весам ребер графа. Для этого мы берем значения из матрицы смежности графа и переносим эти значения в нашу конфигурацию. После этого получаем результат.
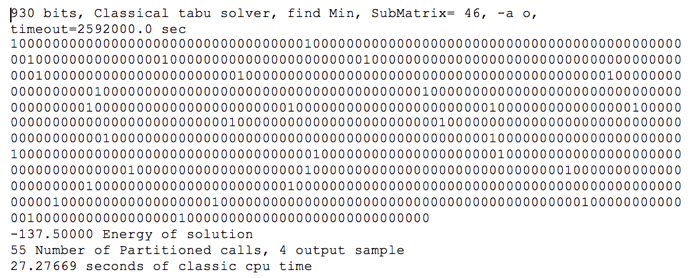
Решение до парсинга

Решение после парсинга
В действительности программирование на квантовом компьютере DWave немного сложнее, так как необходимо учитывать физическое разбиение всего регистра на блоки из 8 кубитов и т.д. Без этого некоторые из комбинаций могут быть не рассмотрены, и в результате мы получим некоторый локальный минимум вместо глобального, но даже такая простейшая программа дает по сравнению с классическими методами отличные результаты.
Мы провели пробный запуск на 14 вершинах на конкретном графе. Алгоритм перебора нашел кратчайший путь длиной 91, время работы заняло примерно 10 мин. Метод Литтла отработал почти мгновенно и дал результат 104. Квантовый алгоритм отработал тоже почти мгновенно и дал результат 97. При этом если программу на квантовом компьютере строить с учетом физических связей, то мы получим результат, аналогичный перебору.
Максимальный граф, который на данный момент мы можем обработать с помощью квантового вычислителя, содержит 44 вершины. На классическом вычислителе в общем случае это займет несоизмеримо большее количество времени, т.к. сложность растет по формуле n!…
Квантовый компьютер, построенный на принципах отжига, имеет большую мощность, чем существующие универсальные компьютеры, но при этом ограничен классом решаемых задач. У нас нет возможности задать первоначальные состояния кубитов или производить над ними какие-то унитарные преобразования — у нас есть только одна возможность — найти комбинацию, при которой значение функции Σhisi + ΣJijsisj при заданной конфигурации окажется минимальным. Однако даже с учетом этого ограничения квантовые компьютеры показывают существенный прирост производительности и могут быть эффективно использованы в задачах оптимизации.
Квантовые компьютеры сегодня
На данный момент существуют следующие основные направления реализации квантовых компьютеров:
- На ионах в одномерном ионном кристалле в ловушке Пауля.
- В полупроводниковых кристаллах бесспинового моноизотопного кристалла кремния
- Кубиты на электронах в полупроводниковых квантовых точках.
- Кубиты на сверхпроводниковых мезоструктурах.
- На одиночных атомах в микрорезонаторах.
- С помощью линейных оптических элементов (оптический квантовый компьютер).
Наиболее проработанными на сегодняшний день являются квантовые компьютеры DWave и IBM Q

DWave имеет статус «аналогового квантового компьютера», так как способен решать лишь узкий круг задач квантового отжига. Но при этом его заявленная мощность составляет 2 000 кубитов.

IBM Q — это программа по разработке универсальных квантовых компьютеров, на которых можно исполнять произвольные квантовые алгоритмы. В данный момент работают системы из 20 кубитов (коммерческое использование), и открытые системы Q Experience на 16 и 5 кубитов. Q Experience cейчас, пожалуй, единственная открытая платформа, позволяющая разрабатывать квантовые алгоритмы. Она представляет собой набор атомарных гейтов, которые можно применять к кубитам.
Использование квантовых вычислений
Помимо описанных ранее сценариев, квантовые вычисления могут отлично работать в других сферах.
Квантовая криптография. Защита информации основана на том, что задача расшифровки не решаема. Квантовая криптография основана на невозможности нарушить законы физики. Один из примеров — обмен секретными ключами BB84. Вася передает Маше набор квантовых частиц. Ревнивый злоумышленник Петя прослушивает канал связи и может перехватить частицы. Но для этого Пете придется измерить их. Он неминуемо разрушит их первоначальное состояние, что станет известно Васе и Маше.
Защита блокчейна. В принципе, она основана на том, что майнерам требуется большое количество времени, чтобы с помощью перебора найти число, при котором хеш блока меньше определенного порога. Это не позволяет подменить блок — пока новый хеш будет вычислен, цепочка уйдет далеко вперед. Квантовый блокчейн за счет параллелизма может мгновенно найти такое число, при котором хеш блока будет недосягаемо мал для классических вычислителей. Таким образом, атаковать сеть можно будет только при захвате 51% квантовых майнеров. А это выводит доверие на новый уровень — сговор более половины игроков с такими возможностями маловероятен.
Известно, что в 2014 году китайские исследователи впервые реализовали распознавание рукописного текста с помощью квантовых вычислений.
Наконец, мгновенная обработка колоссального объема данных и решение задач по оптимизации делают квантовые технологии одним из наиболее перспективных инструментов в области искусственного интеллекта и машинного обучения. По этой причине в 2013 году Google и NASA создали совместную лабораторию по исследованиям в этой области.
Подготовлено по материалам Дмитрия Сапаева, старшего руководителя направления по развитию ИТ-систем в отделе разработки ЦТИ Сбербанк-Технологий, и Дмитрия Булычкова, директора проектов в Центре технологических инноваций Сбербанка.
