[Из песочницы] Оценка премии опционов — аналитические формулы vs моделирование18.12.2017 17:33

Введение

На волне хайпа криптовалют проскакивают новости о торговле биткойном на мировых биржах CME и NASDAQ. Для меня это знаковое событие: руки корпораций, надувавших пузыри доткомов и ипотек, дотянулись и до золота шифропанков — криптовалют. А в арсенале этих самых корпораций мощный рычаг — производные финансовые инструменты, или деривативы.

Находясь под впечатлением прочитанных не так давно историй взлетов и метаморфоз рынков деривативов — прежде всего, фьючерсных и опционных контрактов, я заинтересовался нетривиальным ценообразованием опционов. Мне открылось, что, хотя интернет полон рерайтов статей, толкующих знаменитую формулу Блэка-Шоулза, практических инструментов — web-сайтов, технологических программ или банальных руководств для программиста — не математика, по данному вопросу в интернете недостает. Пришлось вспомнить азы тервера и адаптировать строгие математические описания в популярном, понятном, прежде всего, мне самому, формате.

Определение опциона

Опцион — контракт, дающий покупателю право (но не обязанность!) купить или продать торгуемый на рынке актив по указанной им (покупателем контракта) цене. Продавец опциона назначает покупателю премию — свое вознаграждение за предоставленную покупателю опциона возможность купить или продать актив в определенный срок по определенной цене.
Пример опционного контракта:

покупатель опциона хочет получить право купить 10 Ethereum (ETH) по цене $470 за 1 ETH через 30 дней.
текущая цена Ethereum равна $450.

Допустим, через 30 дней рыночный курс Ethereum вырастет до $500. Покупатель опциона сможет купить 10 Ethereum (10 ETH) по оговоренной в контракте цене $470. После чего, покупатель, желающий сейчас же извлечь выгоду из своей сделки, тут же продаст Ethereum по цене $500, заработав:

10 x (500 — 470) = 300 (USD).

Если же цена Ethereum окажется ниже $470, покупатель опциона просто откажется от невыгодной сделки.

Беспроигрышное предложение! Разумеется, за такую чудесную возможность продавец запросит какую-то сумму — премию по опциону.

Итак, спецификация опционного контракта:

в данном примере покупатель приобрел европейский call опцион в объеме 10 ETH со страйк-ценой $470 USD с экспирацией через 30 дней.
«Европейский» — в данном контексте означает, что покупатель опциона может совершить сделку по указанной цене строго на определенную дату — на момент экспирации опциона. Существуют также «американские» опционы, где покупатель контракта может исполнить его в любое время до момента экспирации, но рассмотрение американских опционов выходит за рамки статьи.
Покупатель опциона получает право купить актив (Ethereum) по указанной цене. Опцион на покупку актива определен как call-опцион, на продажу — put-опцион.
Цена, по которой покупатель опциона имеет право приобрести актив — в нашем примере $470 — называется страйк-ценой.
Сумма, которую покупатель опциона уплатит продавцу, называется премией.

Размер премии по опциону и есть предмет нашего небольшого исследования.

Как продавец оценивает премию по опциону

Рассчитать величину премии — такую, чтобы и самому не остаться в накладе, и не отпугнуть потенциального покупателя «задранным» ценником — настоящее искусство. По крайней мере, было таковым до поры. Пока в 1973 году два математика не явили свету изящную формулу, названную их именами — формула Блэка-Шоулза. Об этой формуле и ее влиянии на рынок деривативов написана даже популярная книга — «Кванты. Как волшебники от математики заработали миллиарды и чуть не обрушили фондовый рынок». Конечно, реальная история несколько сложнее, чем «тьма невежества — вжух! — формула»… Но меня интересуют не столь глобальные процессы, а непосредственно вопрос: насколько формула Блэка-Шоулза применима для оценки «справедливой» премии по опциону, рассчитанной для популярных у трейдеров криптовалютных контрактов?

Модель Блэка-Шоулза описывает некий «стандартизированный» рынок. Выхолощенный, избавленный от резких ценовых перепадов, живущий годами в одном ритме. Разумеется, формула, выведенная для «идеального» рынка, не так хорошо работает на практике, как в теории.

Как принято у трейдеров — там, где недостает теории, обращаются к эмпирике. К трейдерской «чуйке», к «опыту». Как программист, я негодую от такого невежества. Потому приведу свое решение: чужие выкладки, немного тервера, магия Excel и, в самом конце, исходники на C#.

Эталонный расчет — модель Блэка — Шоулза

Википедия снабдит нас формулой. Задав значения переменных опционного контракта и зная параметры торгового актива, мы можем подсчитать «справедливую» премию.

Для дальнейших расчетов нам нужны «идеальные» данные — ценовой ряд, обладающий нужными характеристиками.

Реальная цена, как я уже отмечал, может быть дамой непостоянной: то топчется на месте, то вдруг лихо срывается с места в карьер. Нам же нужен образец идеальной серии ценовых данных как эталон для последующих вычислений.

Логнормальное распределение

Модель Б-Ш (давайте уже сократим имена авторов в названии) предполагает, что ценовой ряд описывает логнормальное распределение. Что это означает? Приведу пример:

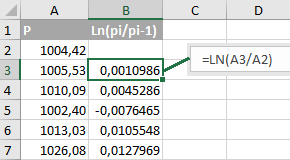
в столбце A — цена абстрактного актива ABS/USD, $inline$p_{i}$inline$.
Столбец B содержит натуральный логарифм от частного $inline$p_{i}$inline$ и $inline$p_{i-1}$inline$.

Логнормальное распределение описывает ценовой ряд, производный ряд от которого, полученный как натуральный логарифм частного от деления текущего значения с предыдущим, имеет нормальное распределение. Сложно. Поясню на нашем примере: если значения в столбце B распределены согласно нормальному закону, то значения столбца A описывает логнормальное распределение.

Как нам получить «логнормальный» ценовой ряд? MS Excel, который я уже использовал для примера, умеет генерировать случайные числа, имеющие равномерное (увы, не нормальное) распределение. Есть несложная методика, по которой мы сможем получить ряд нормально распределенной СВ из равномерно распределенной СВ. Методика называется «метод обратной функции». Не вдаваясь в детали метода, отмечу следующий его важный аспект:

метод обратной функции позволяет получить СВ с произвольным, заданным функцией (таблицей), законом распределения, получая на входе СВ, равномерно распределенную в диапазоне от 0 до 1.

Нам нужна обратная интегральная (как ее еще называют, кумулятивная) функция нормального распределения. Такая есть в Excel: функция «НОРМ.ОБР».

Функция НОРМ.ОБР принимает значения: вероятность, среднее, стандартное отклонение.

Вероятность — то самое значение, от которого мы строим нашу функцию. Строго больше 0 и строго меньше 1. Сгенерируем 999 значений от 0.001 до 0.999 с шагом 0.001 в столбце A. Значения из столбца A и пойдут на вход функции НОРМ.ОБР.
Среднее — математическое ожидание нашей СВ. Напомню, мы генерируем величину, пропорциональную динамике нашего ценового актива ABS/USD. Положительные значения соответствуют росту цены ($inline$p_{i} > p_{i-1} \implies ln (p_{i} / p_{i-1}) > 0$inline$), отрицательные — падению. Если мы зададим параметр «среднее» большим нуля, наш актив будет, скорее всего, расти (программист говорит: проведем миллион итераций и гарантированно увидим конечную цену, превышающую начальное значение). Наш выбор — среднее, равное 0. Что означает «нейтрально дрейфующую» цену ABS/USD.
Стандартное отклонение. О нем тоже пойдет речь впоследствии. Величина, характеризующая волатильность нашего актива. Примем ее равной 0.5% или 0.005. Что примерно соответствует изменению цены в день на ± 0.5% в среднем.

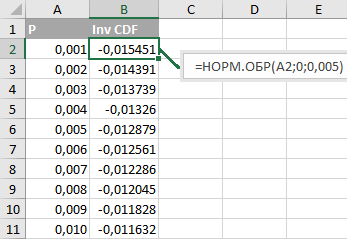
Как интерпретировать эти данные? Возьмем первую пару чисел:

«СВ примет значение -0.015451 или меньше с вероятностью 0.001 (0.1%)».

Вторая пара: «СВ примет значение -0.014391 или меньше с вероятностью 0.002 (0.2%)». И т.д.
Метод обратной функции: мы случайным образом выбираем число в диапазоне от 0 до 1 (столбец A) и находим соответствующее ему значение обратной кумулятивной функции распределения (столбец B). Или же, в нашем случае, просто случайным образом выбираем число из столбца B.

Т.е., выбираем значение N в диапазоне от 0 до 999 и читаем содержимое ячейки $inline$B_{N+2}$inline$:

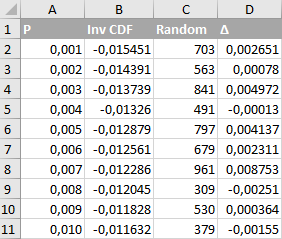
Формула ячейки B2: =НОРМ.ОБР (A2;0;0,005)
Формула ячейки C2: =СЛУЧМЕЖДУ (0;999)
Формула ячейки D2: =ДВССЫЛ (СЦЕПИТЬ («B»; C2+2))

Вот мы и получили нормально распределенную случайную величину с математическим ожиданием 0 и среднеквадратичным отклонением 0.005.

В столбце D может быть сколько угодно значений. Нам понадобится 3650 значений — мы собираемся моделировать дневные изменения цены ABS/USD за 10 лет. Осталось сгенерировать собственно цену ABS/USD.

В столбце D мы имеем ряд величин ∆, а ∆, по формуле логнормального распределения, определена как

$$display$$∆_{i} = ln (p_{i} / p_{i-1})$$display$$

Значит, цены ABS/USD, последующая и предшествующая, будут связаны функцией

$$display$$p_{i} = p_{i-1} * e^∆$$display$$

Перенесем столбец D на новый лист, скопировав его, а затем вставив значения, начиная с ячейки A3.

Теперь укажем начальную цену ABS/USD равную 1000 (USD за 1 ABS) — введем »1000» в ячейку B2:

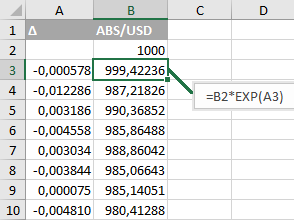
В ячейку B3 введем »=B2*EXP (A3)» и скопируем это значение во все последующие ячейки — B4: B3652.

На этом подготовка исходных данных, наконец, завершена. Столбец B содержит ценовой ряд нашего эталонного актива ABS/USD. Ряд, обладающий характеристиками логнормального распределения со среднеквадратичным отклонением, равным 0.005 (0.5%). У меня получились такие значения:

Нет никакой гарантии, что у вас, если вы проделаете ровно те же вычисления в MS Excel, получатся ровно те же значения, так как исходные данные — случайная величина. И все же — согласитесь, график вполне походит на биржевую сводку?

Расчет премии по формуле Б-Ш

Раз уж у нас есть «эталонные» данные, проведем «эталонный» расчет. Мы считаем премию по «ванильному» европейскому CALL-опциону:

текущая цена (S) равна 1000,
страйк (X) равен 1000. Страйк равен текущей цене, такой опцион на сленге именуется «ванильным»,
экспирация через 30 дней (T),
объем сделки — один контракт.

Наш инструмент ABS — не акция, не облигация и не иная ценная бумага. Никаких дивидендов за обладание ABS владельцу не полагается.

Та самая формула — формула расчета премии за европейский опцион Call (значение C):

$$display$$C=SN (d_{1})-Xe^{-rT}N (d_{2})$$display$$

$$display$$d_{1}=\frac{ln (\frac{S}{X})+(r+\frac{σ^2}{2})T}{σ\sqrt{T}}$$display$$

$$display$$d_{2}=d_{1}-σ\sqrt{T}$$display$$

Разберем параметры формулы.

S и X нам уже известны — текущая (1000 USD) и страйк (1000 USD) цены актива, соответственно.
T — время до экспирации, выраженное, как часть года. К примеру, наш контракт ABS торгуется 365 дней в году, подобно криптовалютным контрактам. Экспирация произойдет через 30 дней, следовательно, T = 30/365 ~ 0.082. Другой пример — опцион на EURUSD на Чикагской бирже, торгуется приблизительно 265 дней в году. Считаем количество торговых дней до конкретной даты — до дня экспирации. Скажем, мы посчитали 23 торговых дня. В таком случае параметр T будет равен 23/265 или примерно 0.087.
r — безрисковая процентная ставка. Как мы уже отмечали, для актива ABS она равна 0.
σ (сигма) — историческая волатильность актива. Здесь потребуется небольшое отступление.

Историческая волатильность

За волатильность мы берем среднеквадратичное отклонение (СКО), пересчитанное на годичный интервал. Приведу очередную формулу из Википедии:

$$display$$S_{0}=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n} 2^{-n}(x_{i}-\overline{x})^2}$$display$$

Как нам посчитать среднеквадратичное отклонение цен ABS/USD в MS Excel?

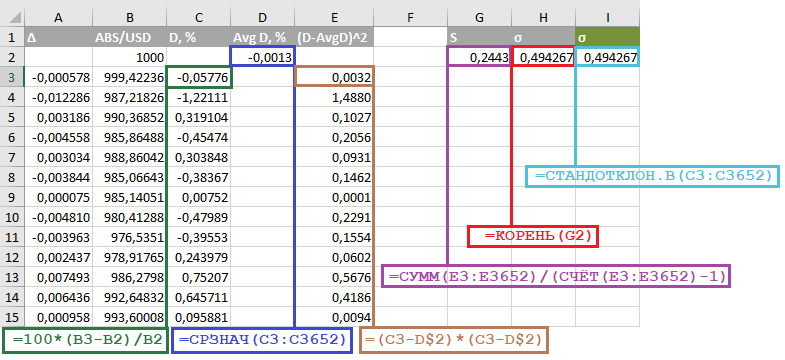
Столбец C содержит разность текущего и предыдущего значения цен ABS, поделенную на предыдущее значение и умноженную на 100%.
Ячейка D2 содержит среднее значение из столбца C.
Столбец E содержит квадраты разности ценового отклонения (столбец C) и среднего значения ценового отклонения (ячейка D2, вторая строка «зафиксирована» в формуле символом $).
Ячейка G2 — дисперсия, сумма квадратов отклонений, деленная на количество значений за вычетом 1 (SIC!).
Наконец, ячейка H2 содержит искомое СКО — корень из дисперсии (G2).

Часть вычислений можно пропустить: достаточно посчитать столбец C (величины отклонений в процентах) и воспользоваться функцией Excel для нахождения среднеквадратичного (стандартного) отклонения — что мы и определили в ячейке I2 — функция «СТАНДОТКЛОН.В».

Осталось пересчитать значение СКО (σ) на интервал один год. Наш ABS/USD торгуется 365 дней в году. Значение σ, рассчитанное для одного дня, надо умножить на корень квадратный из 365:

$$display$$σ_{Y}=σ\sqrt{365}=0,4943\%\times19,105 = 9,443\%$$display$$

Откуда взялся квадратный корень в формуле пересчета дневного значения среднеквадратичного отклонения в годовое? Заинтересовавшихся адресую в интернет, искать модель случайного блуждания, random walk (RW).

Расчет премии в Excel

Теперь, когда мы определили все параметры формулы Блэка — Шоулза, введем их значения и функции в Excel:

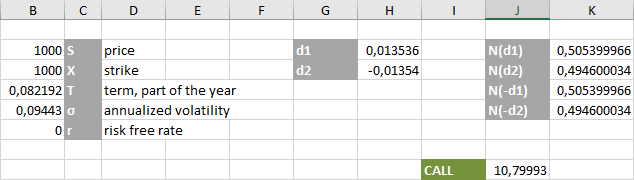
Сразу отмечу: значения T и σ я указываю в абсолютных величинах, не в процентах.

Формула коэффициента d1 =(LN (B2/B3)+B4*(B6+B5*B5/2))/(B5*КОРЕНЬ (B4))
d2 =H2-B5*КОРЕНЬ (B4)
N (d1) =НОРМ.РАСП (H2;0;1; ИСТИНА)
N (d2)=НОРМ.РАСП (H3;0;1; ИСТИНА)
Наконец, премия CALL-опциона: =B2*СТЕПЕНЬ (2,71818;-B7*B4)*K2-B3*СТЕПЕНЬ (2,71818;-B6*B4)*K3

«Справедливая» премия за ванильный European CALL-опцион ABS/USD со страйком 1000 и экспирацией через 30 дней составила $10.80 за один контракт.

Расчет премии для «ненормального» ценового распределения

Выше утверждалось, что ценовая модель Б-Ш адекватна для логнормального распределения ценового ряда. Но насколько близок «реальный» рынок по своим характеристикам подобному закону распределения СВ? Точнее, насколько рынок далек от него?

Наш гипотетический актив ABS/USD характеризуется нормальным распределением логарифмов от частного соседних (текущая и предыдущая) цен. График плотности вероятности появления больших и малых отклонений цены (логарифмов) имеет классическую для нормального распределения форму, примерно такую:

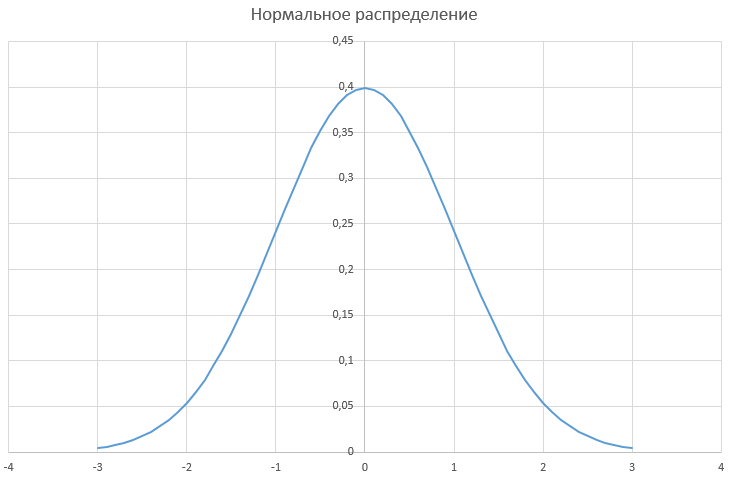
Иначе говоря, имеет форму колокола, с «крутой» вершиной и «плечами», или «хвостами», быстро приближающимися к оси абсцисс по мере удаления от среднего значения (0).

Каким эмпирическим наблюдениям могли бы соответствовать для реального рынка эти самые «хвосты» нормального распределения?

Большие отклонения цены возможны, но имеют крайне низкую вероятность. Для графика, приведенного выше, можно сказать, что отклонение цены на +2% и более имеет вероятность 5%. А отклонение цены на +3% и более имеет уже околонулевую вероятность — какие-то незначительные доли процента.

«Реальному» рынку свойственно несколько иное поведение. А конкретно: большинство ценовых изменений лежат в довольно узком диапазоне, при этом, однако, существенна вероятность значительных ценовых колебаний. График плотности вероятностей ценовых отклонений для «реального» рынка примет вид приблизительно такой:

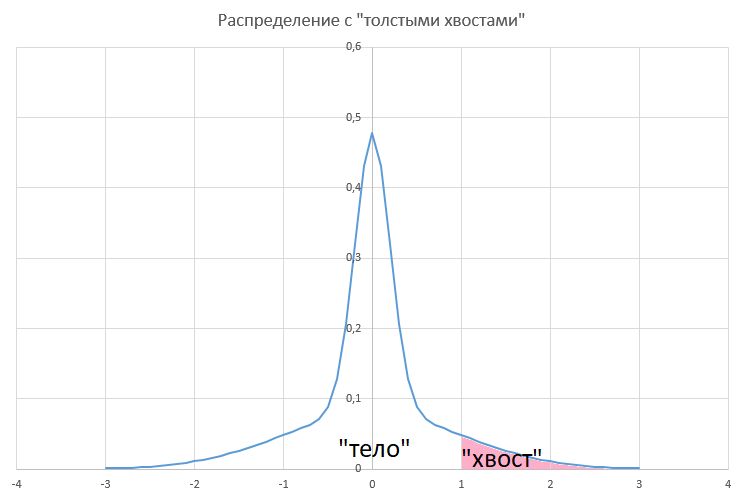
Повлияет ли тот факт, что характеристики распределения дневных отклонений цены для «реального» рынка отличаются от модели Б-Ш на точность расчета?

Очевидно, повлияет. Вопрос — насколько сильно будет ошибаться формула Б-Ш в своей оценке «справедливой» премии?

Моделирование «реальной» цены

Сейчас моя задача — генерировать новый ценовой ряд. Ценовой ряд, логарифмы от частного соседних цен в котором подчиняются некоторому «ненормальному» распределению — распределению, отличающемуся «толстыми хвостами». Более того, я немного усложню себе задачу.

Итоговый ценовой ряд должен характеризоваться той же величиной исторической волатильности, что и ценовой ряд ABS/USD, построенный нами ранее.

Для примера приведу две кривых плотности распределения СВ: нормальное распределение (коричневая линия) и «реальное» распределение (синяя линия) — то, что мы хотим получить. С толстыми и длинными хвостами:

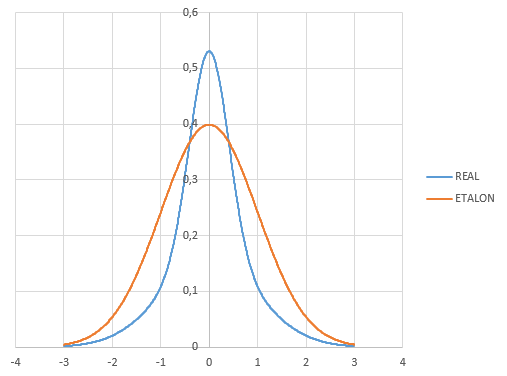
В нормальном распределении мы можем варьировать один параметр — среднеквадратичное отклонение (σ). Вот как выглядят два графика плотности нормального распределения с σ, равной 1 и 0.4 соответственно:

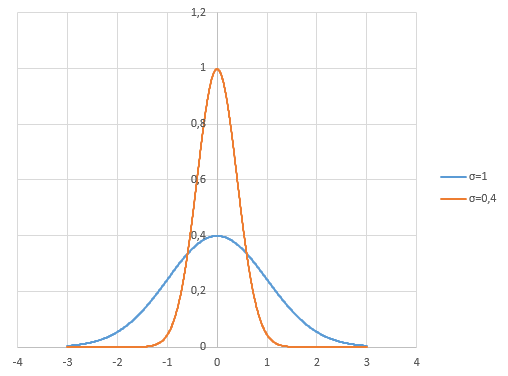
Оба графика — не совсем то, что нам бы хотелось. Тонкое «тело» графика для параметра σ = 0,4 — близко к желаемому. Но нам бы хотелось «хвостов» потолще. Иначе говоря — большой процент отклонений, концентрирующихся в окрестностях среднего значения (0), при все еще значимой вероятности больших (2% и более) ценовых отклонений.

Решение: сложить два графика. Я получу ту самую зависимость, что привел выше на рисунке как «реальную» плотность вероятности распределения цен.

Сейчас мы складывали значения функции плотности нормального распределения. Как же построить распределение, плотность которого будет соответствовать сумме двух функций нормального распределения с параметрами σ = 1 и σ = 0,4?

Очевидно — сложить две случайные величины, имеющие нормальные распределения с разным СКО.

Проделаю примерно те же вычисления, что и раньше, при генерации ряда ABS/USD. Но теперь заполню два столбца функцией «НОРМ.ОБР». Результирующая величина должна иметь годовое среднеквадратичное отклонение, равное 9.44% — как и в предыдущем примере. Этого я добьюсь, проведя несколько итераций подбора параметров, так как результат (сгенерированная выборка) недетерминирован:

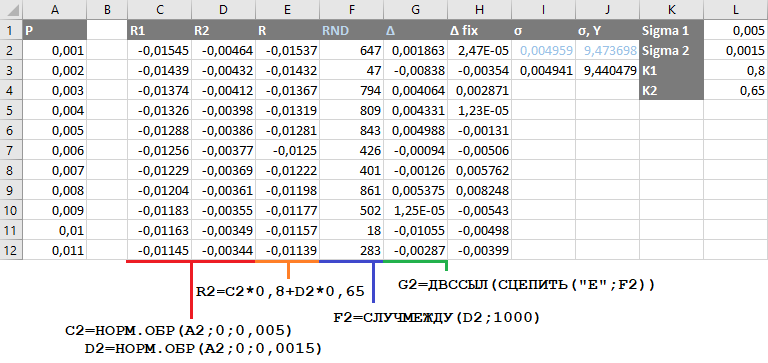
Столбцы C (R1), D (R2) содержат обратную функцию нормального распределения с параметрами 0.005 и 0.0015 соответственно.
Столбец E ® — взвешенную сумму двух этих величин — 0,8 x R1 + 0,65 x R2.
Столбец F (RND) — случайное число в диапазоне от 2 до 1000.
Наконец, столбец G (∆) — случайным образом выбранную из столбца E ® ячейку. То распределение, которого мы добивались.

Осталось применить к полученному ряду формулу:

$$display$$x_{i} = x_{i-1}*e^{∆_{i}}$$display$$

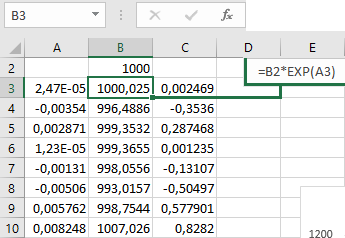
Сумму двух нормально распределенных случайных величин копируем в столбец A. В столбце B, как и раньше, мы умножаем предыдущее значение цены (начинается от 1000) на экспоненту от СВ из столбца A.

В итоге у меня получился следующий график цены WRD/USD:

Премия за опцион CALL для WRDUSD на тех же условиях контракта, что мы уже рассчитали ранее, останется неизменной, так как параметры в формуле Б-Ш не менялись. Напомню цифры: премия за ванильный European CALL-опцион WRD/USD со страйком 1000 и экспирацией через 30 дней составила $10.80 за один контракт.

Мы располагаем двумя активами, динамика цен на которые выражается разными законами:

	ABS/USD	WRD/USD
Закон распределения цен	логнормальное распределение	«Реальное» распределение
Премия по формуле Б-Ш	$10.80	$10.80
«Справедливая» премия	?	?

На этом этапе возможностей MS Excel мне уже недостает, пора переходить к программированию. Продолжение следует…