Квантовое хеширование. Лекция в Яндексе
Одна из сфер, где с появлением квантовых систем могут произойти серьёзные изменения, — механизмы цифровой подписи. В докладе раскрывается алгоритм хеширования, радикально превосходящий аналоги для классических компьютеров. Под катом — подробная расшифровка и слайды.
Бóльшая часть слайдов будет на английском языке, но я думаю, что коллеги меня извинят. Не всегда удается всё переводить, ну и не всегда есть необходимость.
Этот доклад основан на работах, которые здесь представлены. С первой нашей работой — я сам математик — нас пригласили в журнал Laser Physics Letters, который, в отличие от математических высокорейтинговых журналов, имеющих соответствующий индекс чуть меньше 1, имеет индекс 3,2. Сейчас, когда учитываются все Индексы Хирша и прочие, оказывается полезным публиковаться в таких журналах — физических.
Один из последних результатов был опубликован на семинаре Algebra in Computational Complexity, есть такой немецкий центр. Эти результаты можно там посмотреть. Архив — понятная вещь.
Начну с мотивации. Даниил пошутил, что скоро будет квантовый компьютер, и мы все будем им пользоваться. В Казани есть группа, которая собирает компьютеры, и директор, Дьячков Виктор Васильевич. Он сам из Тамбова, очень энергичный. Как меня встретит, говорит: «Фарид, когда мы с тобой будем продавать квантовый компьютер?»
Канадцы уже продают. Вы знаете о компьютере D-Wave, его периодически тестируют, канадцы объявляли, что он сначала был 500-кубитный, а сейчас в нем 1024 кубита. Периодически во время тестирования то оказывается, что все это можно сделать на классическом компьютере, то опять квантовый компьютер у них хорош. Но это все пока в таком состоянии…
Можно сказать, что, наверное, отдельные кубиты — и 500, и 1024, и дальше — можно лепить. Но дело в том, что квантовый компьютер станет хорошим и производящим, очень мощным только в том случае, если эти кубиты будут находиться в сцепленном перепутанном состоянии, состоянии entangled. Содержательно говоря, это ситуация, когда система может программироваться таким образом, чтобы кубиты друг друга чувствовали. Это почти не удается сделать.
Если удастся создать такой квантовый регистр — даже не говорил бы о квантовом компьютере, — где сцепленные состояния будут порядка 500, это уже будет гарантировать такую производительность, при которой можно одновременно работать с состояниями 2500. Это число частиц во Вселенной, и это есть хорошо. Тогда данная система побьет все существующие компьютеры.
Алгоритм Шора, который здесь упоминается, — первый результат 1994 года. Наверняка многие знают, что если у Google или Яндекса спросить, что такое Quantum algorithm zoo, то он сразу выкатит страничку, где более 50 квантовых алгоритмов, которые на порядок лучше существующих классических алгоритмов. Потенциально уже есть набор алгоритмов, которые можно будет запускать на квантовых машинах. И первым стоит алгоритм Шора, алгоритм факторизации. Весь пафос этого дела как раз и начался, когда появился алгоритм Шора. Факторизация означает, что классические алгоритмы RSA будут побиты квантовым компьютером.
В ответ на это сразу возникло такое направление в сообществе криптографии — post quantum cryptography. Есть и книжка такая, здесь указанная. В ней криптографическое сообщество предложило целый набор средств, которые бы боролись с потенциальным квантовым компьютером.
Криптографы в том числе говорят о таком моменте — что, например, схемы подготовки цифровой подписи на основе хеширования, такие как системы подписи Лампорта, не будут биться и квантовым компьютером.
Я вспомню о том, что такое цифровая подпись Лампорта. Это достаточно простая вещь, была предложена в 1979 году. Лесли Лампорт известен как создатель LaTeX, и он наиболее цитируемый человек в области theoretical and practical computer science. Его запредельно цитируют благодаря тому, что он один из создателей LaTeX.
Цифровая подпись Лампорта — система, которая позволяет хорошо подписать биты, 0 и 1. С 0 ассоциируется некое слово w, с единицей другое слово v. Это два закрытых ключа для 0 и 1. Алиса готовит значение функций f (w) и f (v). Предполагается, что нужно взять одностороннюю функцию и эти пары переслать Бобу. Если Алиса хочет подписать 1, то она направляет исходное слово v и 1 Бобу, а Боб, быстро вычисляя по v значение f (v), проверяет, действительно ли это так.
Односторонность очень грубо содержательная. Это означает, что по значению функции аргумент найти сложно, а по аргументу значение функции вычислить легко. На основе него можно проделывать то же самое и с длинными сообщениями…
Следующий шаг, который нам пригодится: мы вспомним, что такое эпсилон-универсальное хеш-семейство.
Возьмем набор N хеш-функций. Под хеш-функцией будем понимать функцию, которая сжимает слова длины К в слова длины М. К > M, здесь возможны коллизии — ситуации, когда два разных слова отображаются в одно слово. Такое случается, когда K > M.
Соберем набор таких хеш-функций. F будет называться эпсилон-универсальным, если выполняется следующее: в ситуации, когда f выбирается равновероятностно из этого множества, вероятность того, что два разных слова дадут одинаковый образ, будет небольшой — не больше эпсилон. Такое семейство называется эпсилон-универсальным хеш-семейством. А в случае, когда эпсилон есть 1/N, это общеуниверсальное семейство.
Используя семейство эпсилон-универсальных хеш-семейств, можно устраивать системы цифровой подписи. Не буду на этом подробно останавливаться. Поговорю о математической части, расскажу, где это реализуется и что за сообщества работают в России.
Центральная идея: мы обобщаем понятие хеширования и хеш-семейств функций на квантовый случай. А суть вот в чем: мы будем отображать слова в квантовые состояния, в ансамбль кубит. Одновременно мы хотим, чтобы выполнялись эти два требования, чтобы коллизии были редки. То есть, содержательно, малейшее изменение слов аргумента должно вести к значительному изменению хеша образа. Так и требуется в классике. И разумеется, функция должна быть односторонней.
Насчет односторонности я перескочил к классике. Понятие односторонней функции, грубо говоря, связано с проблемой P ≠ NP. Если это условие выполняется, то односторонняя функция существует, а в противном случае мы работаем с потенциально односторонними функциями. Такая проблема есть, мы все о ней знаем.
Мы предлагаем конструкцию, которая, в определенном смысле, позволяет строить оптимальные хеш-функции. Мы предлагаем конструкцию, которая, используя классические коды, исправляющие ошибки, позволяет строить целые семейства различных квантовых хеш-функций. Это некий вклад в постквантовую криптографию.
Если алгоритм Шора борется с классикой, то здесь квантовая часть позволяет в каком-то смысле усилить борьбу с будущим квантовым компьютером.
Очень кратко о том, что такое кубит здесь. Кубит — единичный вектор в двумерном гильбертовом комплексном пространстве с таким свойством, что координаты вектора a0 и а1 — комплексные числа, сумма квадратов амплитуд которых равняется единице. Вообще-то комплексное число — двумерное. И, формально говоря, это четырехмерная точка. Но данное соотношение уменьшает размерность до единицы, и в итоге кубит можно представить как вектор в трехмерном пространстве.
Причем это означает, что у него две степени свободы: угол ψ и угол Θ. Всё происходит в полярных координатах. Этот компонент называют амплитудой вещественной, где синус. А этот называют фазой — eiφ.
a0 и а1 — вероятности того, что мы окажемся либо в нуле, либо в единице, если померяем кубит.
В каком-то смысле хорошая аналогия кубита — ситуация, когда мы взяли монетку, подбросили, и пока она летит, она одновременно находится в 0 и 1. Она упала, мы ее померили, классический вероятностный бит перестал жить и проявился либо как 0, либо как 1. Можно и две монетки бросить, но тогда они будут независимые. А система из квантовых битов, если они сцеплены, — есть то, чему нет аналога в классике.
Как можно закодировать слово при помощи одного кубита? Двоичное слово мы интерпретируем как число. Речь идет только о вещественных частях, здесь нет фазовой части. Понятно, что если ψ (w) есть такое число, и если мы его рассматриваем как число по модулю 2k, то слово кодируется в некий единичный вектор, определяемый углом, зависящим от слова, которое мы прочитали. Здесь все нормально. Вот вам способ закодировать слово одним кубитом.
Значит, физически такая кодировка есть односторонняя функция. Существует результат Александра Семеновича Холево — он работает в Стекловском институте. В конце 60-х он показал, что если у нас имеется ансамбль кубит, то максимум классической информации, который можно извлечь из S кубит, — S бит. Я говорю очень содержательно, на пальцах. За этим стоят четкие формулировки.
Значит, если мы имеем один кубит и таким образом загнали туда слово, то из слов длины К мы можем извлечь только 1 бит классический информации. Это как раз и есть физическая односторонность. Здесь два слова кодируются в разных состояниях, такая вот информация.
Что здесь нехорошо? Два разных слова могут кодироваться в близкие состояния, могут казаться неразличимыми. Одного кубита мало.
Все, что я говорил, можно переписать и на языке фазы. Теперь мы не будем говорить о вещественных амплитудах, а возьмем первую часть, вектор с амплитудой 0, вторую — с амплитудой 1, но тут добавим фазу. При помощи фазы можно работать, однако тут нам это не пригодится.
Как такое можно реализовывать? Как можно один кубит настроить таким образом? На самом деле все преобразования есть повороты, они унитарные. Начинаем с нулевого состояния и, считывая на каждом шаге очередной бит…
R1, R2 и так далее нужно указывать разные. Углы получаются разными. Потихоньку наберем углы и в результате получим то, что нам нужно.
Уже имея хорошую одностороннюю квантовую функцию, как бы мы могли подпись Лампорта перевести и проделать это квантово?
По-прежнему выбираем слово w, связываем его с 0, а слово v связываем с 1. Это секретные ключи для 0 и 1. И — заготавливаем открытые ключи. Это уже квантовые состояния, соответствующие слову w: я показывал, как его можно набрать на одном кубите. Слово v набирается так же.
Пересылаем 0 и соответствующее значение квантового состояния 1 Бобу. Обратить процесс невозможно в силу результата Халева. Затем, если хотим, пересылаем Бобу пару слов v и 1. Боб, имея соответствующее состояние и слово v, может проверить, верно ли, что квантовое состояние ψ (v) было получено именно при помощи этого слова. Мы предлагаем здесь реверс-тест.
Поскольку преобразование унитарное, то есть взаимно однозначное… Имеется слово w, заготовлено квантовое состояние, начинаем с нуля, применяем унитарное преобразование, накапливаем нужное преобразование. Получилось соответствующее состояние. Теперь, когда мы получили слово w, Боб, зная алгоритм, может организовать вот такое обратное преобразование. Его легко проделать. И это преобразование он применяет к полученному квантовому состоянию. В результате, если два слова одинаковые, то результатом должно стать состояние 0.
Мы знаем, с каким состоянием сравнивать. Если слова равны, то реверс-тест и соответствующая вероятность того, что они равны, определяются такой формулой: скалярное произведение вектора 0 на состояние обратного преобразования, которое мы получили.
Если два слова одинаковые, это всегда 1 — тут мы не ошибемся. А если состояния не равны, то, имея дело только с одним кубитом, мы все равно можем оказаться близки к единице. Это в том случае, если два состояния, ψ (v) и ψ (w), были близки.
Нам нужно придумать ситуацию, когда два разных слова переводили бы состояние в почти ортогональное ему. Это будет для нас оптимально.
Следующий шаг — когда нам одного кубита не хватает и нужен регистр из S кубит.
От одного кубита мы можем перейти к такой системе. Значит, мы работаем в гильбертовом пространстве размера 2s и соответствующий ансамбль описывается так же, как в случае с одним кубитом. ai есть амплитуда, комплексные числа. Норма этого вектора — по-прежнему 1. Нормы этих чисел в квадрате есть вероятность получить одно из базисных состояний i, если мы его померяем.
То есть можно говорить о том, что теперь мы будем рассматривать функции, которые устроены следующим образом: слова длиной К отображаются в ансамбль из S кубит. Запись будет вот такая.
Не буду говорить, как это было организовано: такое можно сделать по аналогии с тем, как это было сделано для одного кубита.
Результат теперь такой. Чего мы будем требовать? Мы будем называть функцию ψ, которая отображает слова длиной k в ансамбль из S кубит, δ-Resistant (|Σk|, s)-квантовой функцией — если выполнилось условие, что два разных слова длины k порождают состояние, которое почти ортогонально, дельта-ортогонально.
Эта ситуация будет обеспечивать следующее условие. Если мы потом, для проверки, начнем применять к ним так называемый реверс-тест, то будет ли верно, что два состояния одинаковы? Вероятность того, что мы скажем «да», окажется не больше, чем дельта-квадрат для разных слов. Если слова одинаковые, то мы будем говорить «да» с вероятностью 1. Это как раз то, что нам нужно.
Теорема доказывается достаточно просто. Оказывается, если мы хотим строить такие δ-Resistant (|Σk|, s)-квантовые функции, то s не может быть меньше, чем log (k) — log (log (1 + √(2/1 — δ))) — 1.
Нижняя оценка есть. Можно ли строить такие хорошие дельта-устойчивые квантовые функции, которые близки к теоретической нижней оценке? Удивительно, но оказывается — можно.
Забегая вперед, я объявляю результат, который говорит, что если у нас есть исправляющий ошибки линейный код, который устроен так, что слова длины k кодируются словами длины n и мы работаем в соответствующем поле Fq, то тогда мы можем для любого заранее выбранного δ и для такого Δ, которое связано с характеристиками этого кода d от хеммингового расстояния n, построить длину кода. При этом число кубит, которое нам для этого потребуется, — не больше, чем log (n).
Вновь забегая вперед — мы результат реализовали, посмотрели, как это будет выглядеть на очень красивом коде Рида-Соломона. И оказалось, что для него получаются следующие характеристики. Если длина кода на константу больше длины исходного сообщения, то для такого порога ошибки, как k-1/q + Θ, мы можем построить соответствующий квантовый хеш-код с характеристиками log (q log (q)) и неким довеском. И вещь эта достаточно близка к нижней оценке, которая здесь присутствует.
Это для нас оказалось удивительным. Когда я это рассказывал на семинаре в физико-технологическом институте, Александр Семенович Холево, услышав нижнюю оценку, сказал: правдоподобно, да, —, а как конструировать? Когда мы с ним обсудили вариант, что это, например, можно сделать с использованием кода Рида-Соломона, он согласился, что кое-что в данном направлении сделать удалось.
Это описание доклада, который здесь представляется. А теперь я чуть более подробно поговорю вот о чем…
Первый пример был такой: имеем слово, хешируем его в один квантовый бит. Теперь нужно, имея ансамбль из s кубит, определить, каким образом туда все это кодировать и хешировать. Что за механизм такой должен быть? Для ответа на такой вопрос мы предлагаем понятие квантового хеш-генератора.
Первые примеры. Как всегда, оказывается, что в мире что-то такое было, но говорилось немножко на другом языке. Возникло такое понятие, как quantum fingerprinting или квантовые отпечатки пальцев. Это было в 2002 году сделано Гарри Бурманом с соавторами для специальной коммуникационной модели вычисления с арбитром. И оказалось, что это — специальный двоичный случай квантового хеширования.
Одна из задач в теории кодирования — перейти от двоичных кодов к более чем двоичному алфавиту. Коды Рида-Соломона принципиально не двоичные, тут игра качественная. Когда мы переходим к полю другой характеристики, больше чем 2, то оно здесь действительно продвигается.
Я покажу первые примеры того, что было сделано. А затем покажу, как перейти от кодов, исправляющих ошибки, и вложиться в эту конструкцию.
Есть эпсилон-универсальное хеш-семейство. Используя некое семейство функций, я начну генерировать одну квантовую функцию. Есть набор классических линейных функций, есть поле Fq. Из него берем коэффициенты и имеем набор функций H = {h1, …, hT}. Теперь при помощи функции h мы генерируем однокубитные квантовые функции вот таким образом. Для простоты я буду работать не с фазами, а с вещественными амплитудами. В каком-то смысле это интуитивно понятно, хотя физики для своей реализации попросили переписать это все на язык фазы, потому что фазовую вещь легче реализовывать.
Теперь мы заготавливаем набор таких квантовых функций: |ψhj (w)⟩ = cos2πhj (w)/q|0⟩ + sin2πhj (w)/q|1⟩.
Затем собираем эти функции в одну таким образом: |ψH (w)⟩ = 1/√T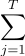
|j⟩|ψhj (w)⟩.
Содержательно эта запись означает, что мы равноамплитудно или равновероятностно одновременно запускаем вычисления всех этих T-функций h. И выстраиваем вычисления таким образом — квантовая физика позволяет это сделать. Перед нами математическая запись того, что физика позволяет сделать.
Регистр j нужно трактовать как двоичную запись числа j. А раз так, то нам достаточно иметь log (T) бит, им соответствует состояние кубита. Не буду говорить подробно, как это сделано. И log (T) кубит руководят вычислением последнего кубита. В соответствующем подпространстве каждое из подпространств управляет вращением одного последнего кубита — в котором завернута вся информация. Последний кубит вращается всеми этими T возможностями — они таким образом обеспечивают log (T) квантовых бит.
Перейду к конкретному примеру, который был предложен Бурманом, Кливом, Уотросом и де Вольфом. Они взяли произвольный исправляющий ошибки двоичный код с хэмминговым расстоянием d, слова длины k в котором кодируются словами длины n, и рассмотрели как раз то, что я показал на предыдущем слайде.
Одновременно работает система из log (n) кубит. Каждый регистр — такой, что он вращает последний кубит в соответствии со значением Ei (w). Поскольку этот код — двоичный, то поворот осуществляется только на 90 градусов. Либо последний кубит остается в нуле, либо поворачивается на 90 градусов. И этот ансамбль заворачивается в систему из log (n+1) кубита, который управляет поведением последнего.
Но они на этом языке не говорили, у них была другая задача, их конструкция переписывается таким вот образом. И оказалось, что эта функция хороша. Она дельта-устойчивая для слов длины k, если мы имеем s кубит и если s вот такое. Здесь все хорошо.
Следующий шаг мы делали с Сашей Васильевым. Он в 2009 году, используя эту конструкцию, защитил диссертацию. Мы тоже не знали тогда, что это хеширование, а отображали квантовые отпечатки пальцев на случай произвольного конечного поля. Была придумана конструкция. Как всегда, оказалось, что эта конструкция, будучи совсем на другом языке, была использована Ави Угдерсоном и Разборовым в 1993 году для других задач. Фактически интерпретируя их результат на нашем языке, мы говорим, что можно подобрать некое небольшое множество порядка log (q) из таких функций: T = ⎡(2/δ2) ln (2q)⎤.
Тем самым множество таких линейных функций, не очень большое в сравнении с log (k), позволяет образовать очень хорошую общую квантовую хеш-функцию. Она дельта-устойчивая, и она кодирует слова в множестве q, элементы поля интерпретируются как слова длиной log (k), и здесь достаточно иметь s кубит.
Обобщая эти конструкции, мы получаем следующее: появляется понятие квантового хеш-генератора. Мы будем говорить, что семейство функций G — квантовый хеш-генератор функции такого вида. Если мы можем построить подобные для каждой функции и каким-то образом отобразить их в ансамбль из l кубит, а также, собрав их вместе, получить квантовую хеш-функцию, которая является дельта-устойчивой с такими характеристиками, что слова длины k кодируются в d+l квантум-бит, — то такое семейство мы будем называть квантовым хеш-генератором.
Определение таковó, что конструкция Бурмана и его соавторов и наша конструкция 2008 года укладываются в это понятие.
Если мы имеем квантовый хеш-генератор, эти функции можно строить по-разному. Скорее всего, хеш-генератор неоднозначно определяет квантовую хеш-функцию. На эти темы можно разговаривать дальше.
Теперь — центральная теорема, которая всё увязывает вместе. Первое условие: мы берем эпсилон-универсальное хеш-семейство, которое имеет такие характеристики, N функций, и при помощи них кодируем слова длины k в поле Fq. Второе условие: в качестве Н мы берем некий уже готовый квантовый хеш-генератор —, а такие есть. В частности, нам удобнее брать тот квантовый хеш-генератор, который мы с Александром Васильевым придумали.
Устраивая суперпозицию этих двух семейств, мы сначала применяем функции семейства F, а затем заворачиваем их в функции из множества Н. Тогда новое семейство является квантовым хеш-генератором с вот такими характеристиками. Оно дельта-устойчивое, оно кодирует слова длины k в ансамбль из s кубит. Δ ≦ ε + δ — это соответствующая характеристика эпсилон-универсального хеш-семейства и дельта-характеристика дельта-устойчивости уже готового квантового хеш-генератора, который мы берем. Ну и число кубит зависит от числа функций в эпсилон-универсальном семействе и от числа функций в готовом квантовом хеш-генераторе.
Причем здесь нам требуются логарифмы от числа соответствующих функций. Это в определенном смысле гарантирует, что квантовые хеш-функции экспоненциально дешевле строить, чем иметь такие вещи исходно.
Появилась целая группа новых примеров, которая использовала конструкции, существующие в computer science. Фрейволд, математик из Риги, в 1979 году предложил функцию, которая называется «классический fingerprinting», основанную на том, что мы хотим сравнить два разных слова и сравниваем их по разным модулям. Здесь играет китайская теорема об остатках. Я об этом много говорить не буду, но если два слова равны, то они по любому модулю pi равны небольшим модулем. А если два слова не равны, то для большинства pi соответствующие значения тоже не равны.
Первая работа была опубликована в сборнике «Проблемы кибернетики» на рубеже 70–80-х годов и, я помню, достаточно хорошо рассказывалась на семинаре у Олега Борисовича Лупанова в МГУ.
Оказывается, что это семейство является, конечно, универсальным хеш-семейством с такими характеристиками, 1/с-универсальным семейством, где с — соответствующий способ выбора числа всех функций. А раз это эпсилон-универсальное хеш-семейство, то, комбинируя его с семейством, которое мы с Александром Васильевым придумали и которое, в свою очередь, основывается на результатах разбора Вигдерсона, можно выяснить, что при помощи семейства классического fingerprinting Фрейволда порождается квантовая хеш-функция с такими характеристиками: дельта-устойчивая, слова длины k отображаются в s кубит. Дельта зависит таким образом: дельта маленькая — это характеристика нашего семейства, 1/с — характеристика Фрейволда, вот столько кубит достаточно и нижняя оценка — вот такая. Нижняя и верхняя оценка здесь достаточно близки. Оказалось, что конструкция Фрейволда хороша.
Классические хеш-семейства, основанные на конструкции Фрейволда, не используют в практике, потому что имеется много простых чисел, нужно их все держать. Используются немного другие характеристики, например очень известное семейство — универсальное линейное хеш-семейство.
Во всех учебниках по алгоритмам есть такой пример. Он был предложен создателем универсальных хеш-семейств Калтором и Вегманом в 1979–1980-х годах — что совокупность таких линейных функций есть универсальное классическое хеш-семейство. Доказательство простое и красивое.
Разумеется, мы берем его, наше семейство, которое мы с Сашей Васильевым придумали. Вот оно. В результате получается такая конструкция. Получается квантовый хеш-генератор, который генерирует квантовую хеш-функцию с такими характеристиками. Это характеристика линейного универсального семейства, а дельта — наша характеристика. Верхняя оценка такая, число кубит — то, которое здесь нужно.
И оказалось, что это семейство экспоненциально дороже имеющейся нижней оценки. Нижняя оценка — log (k), а здесь верхняя оценка — k. Такие известные и используемые вещи, оказывается, в квантовом мире лучше не применять.
Вот и результат, который я в начале анонсировал. Если есть исправляющий ошибки линейный код n-k-d, который слова длины k кодирует в слова длины n, работая в поле Fq, то тогда есть квантовый хеш-генератор. А значит, мы можем строить соответствующую квантовую хеш-функцию, которая обладает такими свойствами, что устойчивость определяется величиной Δ = (1 — d/n) + δ. Это характеристика кода, исправляющего ошибки, а δ — характеристика семейства, которое мы используем. s, в свою очередь, вот такое: s ≦ log (n) + log (log (q)) + 2*log (1/δ) + 4.
Доказательство основано на результате 1994 года, который говорит о том, что если мы имеем код, исправляющий ошибки, с соответствующими характеристиками, то тогда мы можем построить и универсальное хеш-семейство. И наоборот: если мы имеем универсальное хеш-семейство с такими характеристиками, то мы можем построить соответствующий код, исправляющий ошибки.
Универсальные хеш-семейства определились и появились на рубеже 70–80-х годов. Коды, исправляющие ошибки — это, в свою очередь, классика: все именные коды появились на рубеже 50–60-х годов. Удивительно, что такая очень простая связь была обнаружена только в 1994 году. Кто знает, тот знает, а если нет — полезно почитать. Будет интересно.
Используя эту теорему, берем код Рида-Соломона — он очень красивый, во всех учебниках и курсах рассказывается — и строим хеш-генератор, соответствующую ему хеш-функцию.
Это то, что я анонсировал в первой части рассказа. Такая конструкция оказалась оптимальной.
Итак, мы теперь можем все это распространить и на другие конструкции. Их много. В частности, меня спрашивают, почему не Рида-Маляра. Разумеется, его тоже можно. Бодчи-Удхури — конечно, тоже все ложится, красиво. Но код Рида-Соломона — слишком классический. Хоть в школе рассказывай.
Это можно расписать детальнее. Можно и почитать, нет смысла говорить подробно.
Вот над чем мы работаем и куда все это двигается. Я специально написал такую шпаргалку. Начать с того, что этот текст я, разумеется, оставляю и если есть вопросы — скажу по нему.
Какие реальные физические проблемы здесь появляются? Физики сейчас работают над так называемой квантовой памятью. Они понимают ее так, что носителем кубита является фотон. Он прилетает в вещество, и вещество его поглощает. Через некоторое время, воздействуя на это вещество, можно излучить фотон в точно таком же состоянии. Состояние фотона есть состояние кубита.
И если такие вещи выстраиваются, это есть усилитель сигнала, репитер. Сейчас речь идет о построении квантовых репитеров. На 100 км по оптоволокну идут фотоны, потом они поглощаются, начинают пропадать. Если через каждые 100 км поставить такой квантовый репитер, который повторяет сигнал, решится проблема передачи информации. Итак, первая задача — построение репитера.
До квантовых компьютеров, на которых можно будет реализовывать Шора, пока далеко. Первая задача — выстроить квантовый репитер. Что с квантовым репитером можно сделать? Вещество поглотило, перед излучением можно на него воздействовать, преобразовать состояние и извлечь уже в новом состоянии. Сейчас идет борьба о том, что если с десяток кубит, ансамбль, можно запомнить и извлечь, то такое количество будет нормальным для построения хеш-функции.
Смотрите, если s порядка 10, то для каких полей это уже можно делать? Или если s порядка 100? Технологии сейчас, похоже, приближаются к тому, что при десятке и сотне уже можно будет работать. Если s окажется порядка 100 с использованием такого чисто теоретического результата, как код Рида-Соломона, то какие функции можно будет устойчиво хешировать — и с какими полями?
Сразу могу сказать, с кем мы сотрудничаем. В Москве это МГУ и Международный лазерный центр МГУ. На ВМК академик Валиев организовал кафедру квантовой информатики, после его смерти образовалась кафедра… не помню, как называется. Воеводин занимается супервычислениями, суперкомпьютерами. Внутри сохраняется сообщество, которое работает в области квантовой информатики.
В Стекловском институте Семенов, Александр Семенович Холево, разумеется. И центральным становится Физико-технологический институт РАН. Он сейчас хорошо курирует эти вопросы, мы активно взаимодействуем. Но получается, что все, кого я перечислил, — это в основном люди, которые пришли сюда из физики. Мы алгоритмы можем предложить, но до алгоритмов нужна хорошая физика. Речь сейчас идет о технологии.
И есть соответствующая лаборатория, отдел в Академии криптографии РФ. Хорошая группа в Черноголовке, в Новосибирске, в ИТМО. Есть серия конференций «Квантовая криптография» в мире. В этом году конференция проходила в Париже, в будущем году пройдет в Токио, и т. д. В Цюрихе проходила, в Сингапуре. Комьюнити там составляют группы, которые занимаются вопросом квантовой передачи ключа. Известен такой квантовый протокол ВВ-84, Бене-Броссарда. Они его в 1984 году изобрели, а сейчас вокруг него целая конференция: больше ста человек собирается и физики соревнуются в реализации подобных вещей.
Тут уже алгоритмов не так много, происходит физическое вылизывание всего этого. И сейчас все ждут, когда наконец то, что называется квантовой памятью, будет готово, когда можно будет это дело экспериментально во многих местах повторить, начать выстраивать протоколы.
В Казани есть группа, которая занимается именно вопросами квантовой памяти. Их сейчас больше всего интересует работа с фазами, они на этом языке могут устраивать достаточно хорошие эксперименты.
Лаборатории почти готовы, но получилось так, что доллар стал вдвое дороже, и хорошее оборудование, которое ребята хотели заказать раньше, теперь никак не получается приобрести. Но это следующий вопрос.
Пожалуй, всё. Спасибо.
— Как вы оцениваете вероятность перехвата зашифрованной информации в создании алгоритма раскриптовки ключа?
— Я взаимодействую с Сергеем Куликом из Международного лазерного центра. Я не специалист в области физики, но классический уже алгоритм ВВ-84 — ребята сказали, он полностью разваливается. В области физики есть целые группы работ, на основе которых они почти всё сделали заново. ВВ-84 хорош, чтобы рассказывать студентам принципы. То есть, как всегда, есть теоретическая учебная криптография, а когда речь д
