Квантование эмбеддингов: что это, зачем оно нужно и как его правильно готовить
Что такое эмбеддинги?
Эмбеддинг — числовой вектор, который каким-то (в общем случае непонятным на глаз) образом характеризует интересы пользователя или контент. Например, эмбеддинги могут быть такими.

У каждого пользователя и карточки может быть несколько эмбеддингов разных типов. В основном используются два вида эмбеддингов.
Контентные — на основе контента карточки в ленте (заголовок, текст, картинка, тема). У двух статей с похожим заголовком о самолётах эмбеддинги будут близки.
Коллаборативные — на основе оценок похожих пользователей и карточек (лайков, дизлайков, кликов, блокировок). У двух статей эмбеддинги будут близки, если статьи нравятся пользователям с близкими интересами.

Зачем нужны эмбеддинги?
Расскажу поверхностно (настолько, насколько необходимо для этого поста), потому что о факторизации матриц и принципах работы рекомендательных систем уже написано много прекрасных статей. Например:
- тут Павел Пархоменко parkhomenkopa понятно и кратко объяснил смысл алгоритма ALS;
- тут Михаил Ройзнер MRoizner основательно рассказал об устройстве рекомендательных систем;
- тут Никита Мокров Tismoney развёрнуто описывает разные способы факторизации матриц.
Дзен — это рекомендательная система. Её задача — найти материалы, которые с наибольшей вероятностью будут интересны пользователю.

Например, так выглядит моя лента
Чтобы выбрать такие карточки, мы предсказываем оценку пользователя для всех карточек и выбираем карточки с лучшей оценкой.
Для решения этой задачи используется матрица оценок (позаимствована из поста Паши):

В ней по строкам расположены пользователи, по столбцам — карточки, а на пересечении — оценки, которые пользователи поставили карточкам. Большинство оценок мы не знаем — нам нужно их предсказать.
Реальная матрица оценок в Дзене весила бы больше 100 ТБ. Такую матрицу тяжело поместить на диск одной машины, что уж говорить о памяти. Но, поскольку матрица по большей степени пустая, мы можем применить алгоритмы факторизации матриц, такие как ALS (Alternating Least Squares), чтобы эффективно использовать её для предсказаний.
Вместо этой тяжёлой матрицы мы возьмём две другие — P и Q, которые при перемножении дадут матрицу, близкую к исходной матрице оценок. P — матрица пользовательских эмбеддингов, а Q — матрица эмбеддингов карточек.
Выбирая длину эмбеддинга (d), можно найти оптимальный баланс между качеством аппроксимации матрицы оценок и её размером. Использовать эмбеддинги при вычислениях намного удобнее: чтобы построить рекомендации для одного пользователя, нам не нужны эмбеддинги других пользователей. Хранить эмбеддинги удобно в шардированных key-value хранилищах.
Квантовать-то их зачем?
Мы считаем эмбеддинги пользователей и карточек в офлайне, потому что некоторые эмбеддинги считать в рантайме дорого, а другие невозможно. У каждого пользователя и каждой карточки есть несколько десятков эмбеддингов. Каждый эмбеддинг — массив примерно из 100 чисел с плавающей запятой (float). Соответственно, весит один эмбеддинг около 400 Б.
Для ранжирования нам нужны эмбеддинги где-то семи миллионов карточек. Они весят суммарно около 100 ГБ. Эмбеддинги карточек слабо меняются во времени (контентные эмбеддинги меняются только при редактировании карточки). Просто хранить эмбеддинги карточек в БД нельзя, потому что на каждый запрос придётся вычитывать их все в память. Поэтому мы храним их все в памяти на каждой машинке, шардируя по типу карточки.
Эмбеддинги пользователей меняются после каждого взаимодействия с лентой Дзена (лайк, клик и даже показ карточки). Их мы считаем в стриминговом процессинге и складываем в специальное распределённое in-memory key-value хранилище. На один запрос нужно считать из хранилища несколько десятков пользовательских эмбеддингов (эмбеддинги пользователя, для которого подбираем рекомендации). Поэтому их необязательно хранить в памяти каждой машинки, да это и невозможно — мы храним эмбеддинги для примерно 300 миллионов пользователей, а это больше 10 TБ памяти. Эмбеддинги пользователей хорошо шардируются по хешу от user_id.
С точки зрения использования эмбеддингов архитектура рантайма Яндекс.Дзена выглядит примерно вот так (конечно, это очень упрощённая схема).
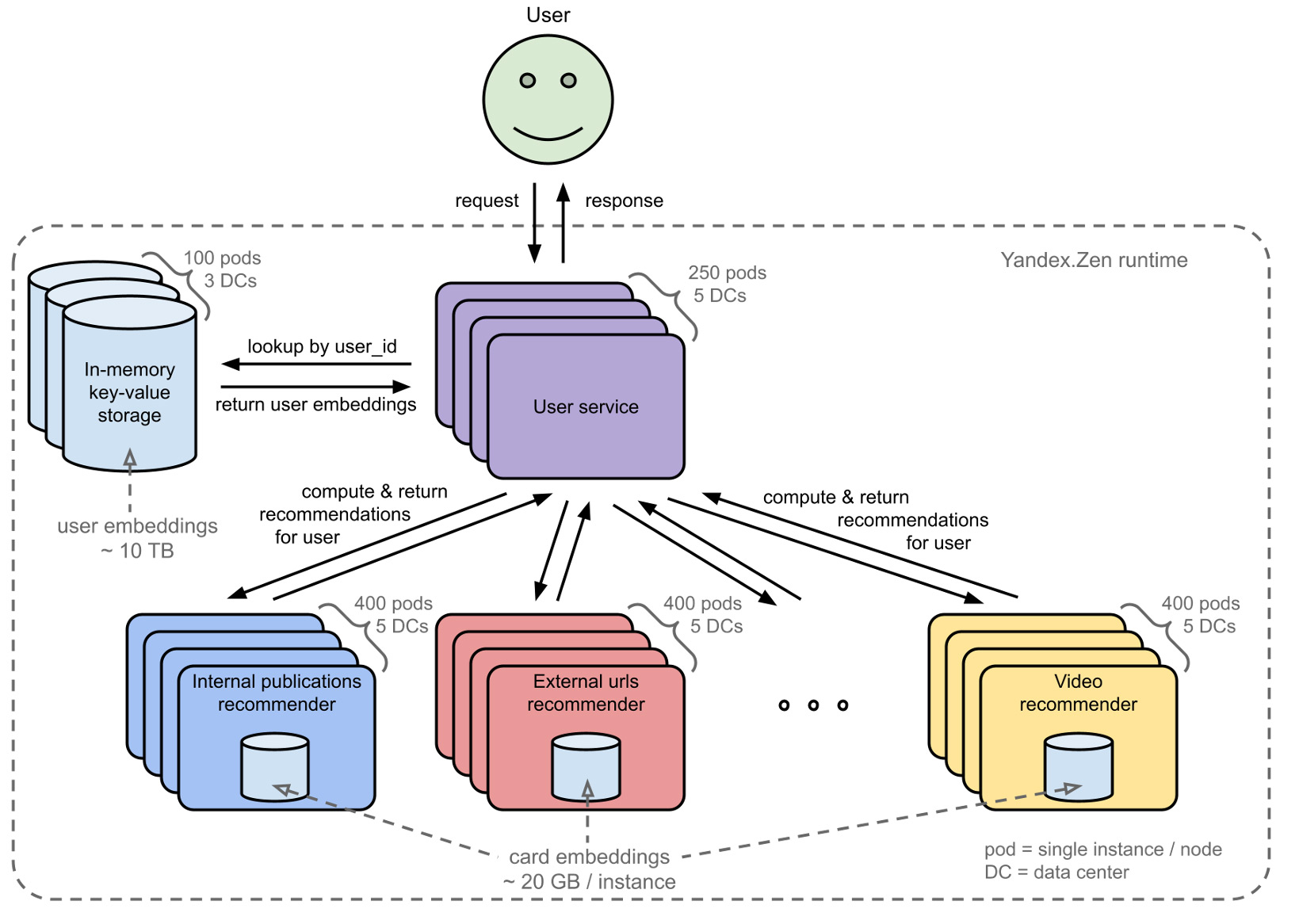
На картинке можно разглядеть несколько узких мест.
- Эмбеддинги пользователей съедают много памяти в хранилище. 10 ТБ памяти стоят существенных денег.
- Эмбеддинги карточек съедают много памяти на инстансах рекоммендеров. Из-за большой избыточности тут получается аж 24 ТБ памяти суммарно. Более того, необходимость иметь на каждом инстансе эмбеддинги всех карточек одного типа усложняет горизонтальное масштабирование.
- Эмбеддинги пользователей летают по сети, съедая около 300 МБ/с сетевого трафика.
- Хоть на этой картинке и не видно, рейт записи пользовательских эмбеддингов в WAL-журналы на SSD (внутри хранилища) тоже дорогой ресурс. Рейт записи — около 300 МБ/с.
А вдруг можно сжать эмбеддинги, существенно не ухудшив качество рекомендаций?
Тут нам и поможет квантование. С помощью квантования можно преобразовать непрерывный диапазон значений в набор дискретных величин фиксированного размера. Проще говоря, преобразовываем float (четыре байта) в byte (один байт).
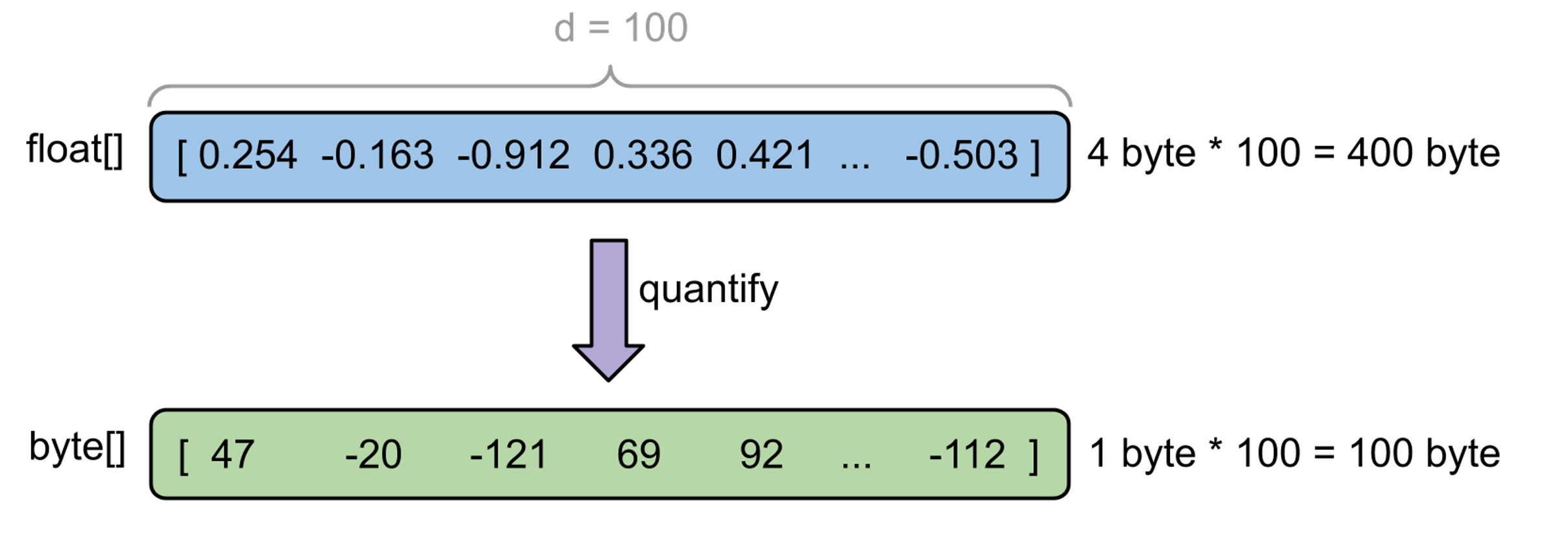
Оказалось, что существуют методы квантования, которые могут сжать наши эмбеддинги в четыре раза, не просадив существенно качество рекомендаций.
Визуализируем эмбеддинги
Для начала нужно понять, с чем мы имеем дело, — внимательно посмотреть на структуру эмбеддингов.
Эмбеддинг можно визуализировать, например, так: 
На левом рисунке вдоль оси Х расположены индексы, вдоль оси Y — значения эмбеддингов на этих индексах (розовые точки). На рисунке видно уплотнение точек по всем индексам в области 0. Для удобства оценки степени уплотнения нарисованы линии максимальных и минимальных значений (maxs и mins) и некоторые перцентили (1p — первый перцентиль).
Правый рисунок — гистограмма значений только на 42-м индексе для наглядности. Вспомогательные линии (минимумы, максимумы и перцентили) нарисованы аналогично.
Распределение внутри всех индексов куполообразное. Иногда похоже на нормальное, но в общем случае это не так.

У других типов эмбеддингов встречаются усложнения. Например, разброс значений может значительно изменяться от индекса к индексу. Купол может быть широким или узким. Вершина купола не всегда в нуле, и она также может значительно изменяться от индекса к индексу.
Мы исследовали в основном три алгоритма квантования, сейчас о них расскажу. Названия придумали, как смогли.
Квантование min-max
Вероятно, первая идея, которая может прийти в голову, — вырезать интервал между минимальным и максимальным значением и поделить его на равные отрезки.
Для каждого индекса преобразование будет выглядеть примерно так: 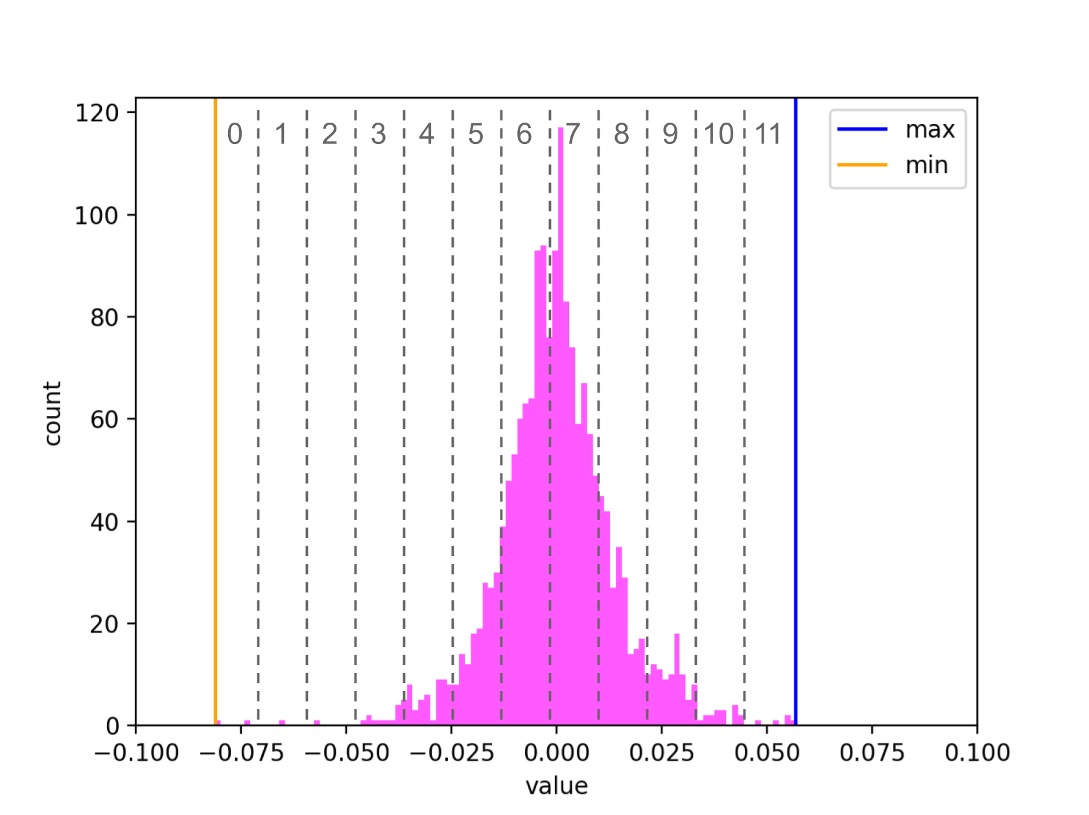
На рисунке серые числа между пунктирными линиями обозначают номер отрезка, в который попало значение эмбеддинга. Этот номер и есть квантованное значение. В реальности отрезков будет 256, а не 12.
Формально преобразование можно выразить так:
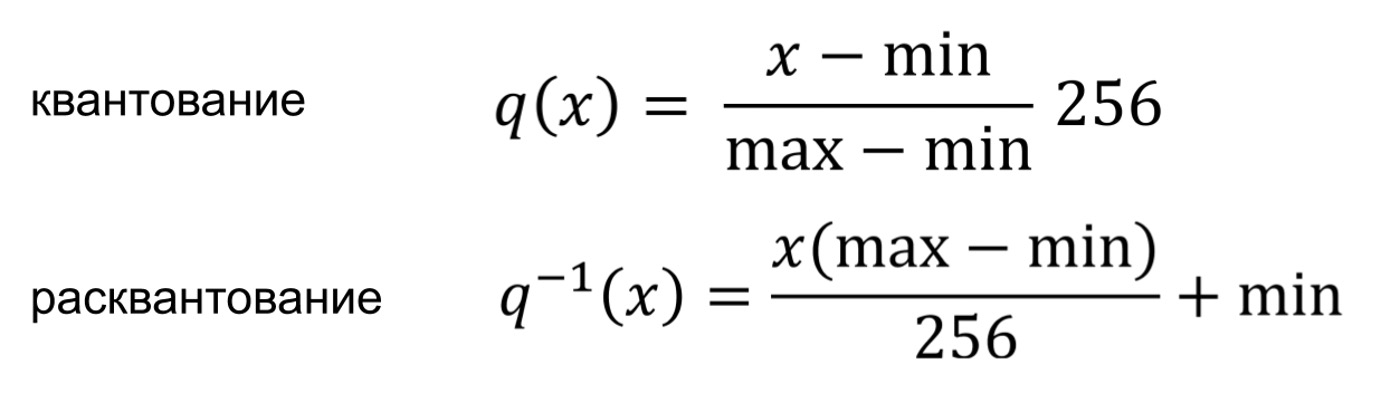
Оба преобразования представляют собой простые линейные смещения на каждом индексе эмбеддинга.
Для всех индексов значения min и max могут существенно отличаться (как видно из распределений выше). Поэтому для каждого типа эмбеддинга нам нужно хранить два вектора размером d с минимумами и максимумами (примерно 800 Б на каждый тип эмбеддинга).
Такой подход прост в реализации и не требует много ресурсов на преобразования.
Однако есть очевидный недостаток — для некоторых типов эмбеддингов существенная доля значений будет попадать в пару-тройку центральных отрезков. В таком случае мы потеряем полезную информацию о пользователе или карточке.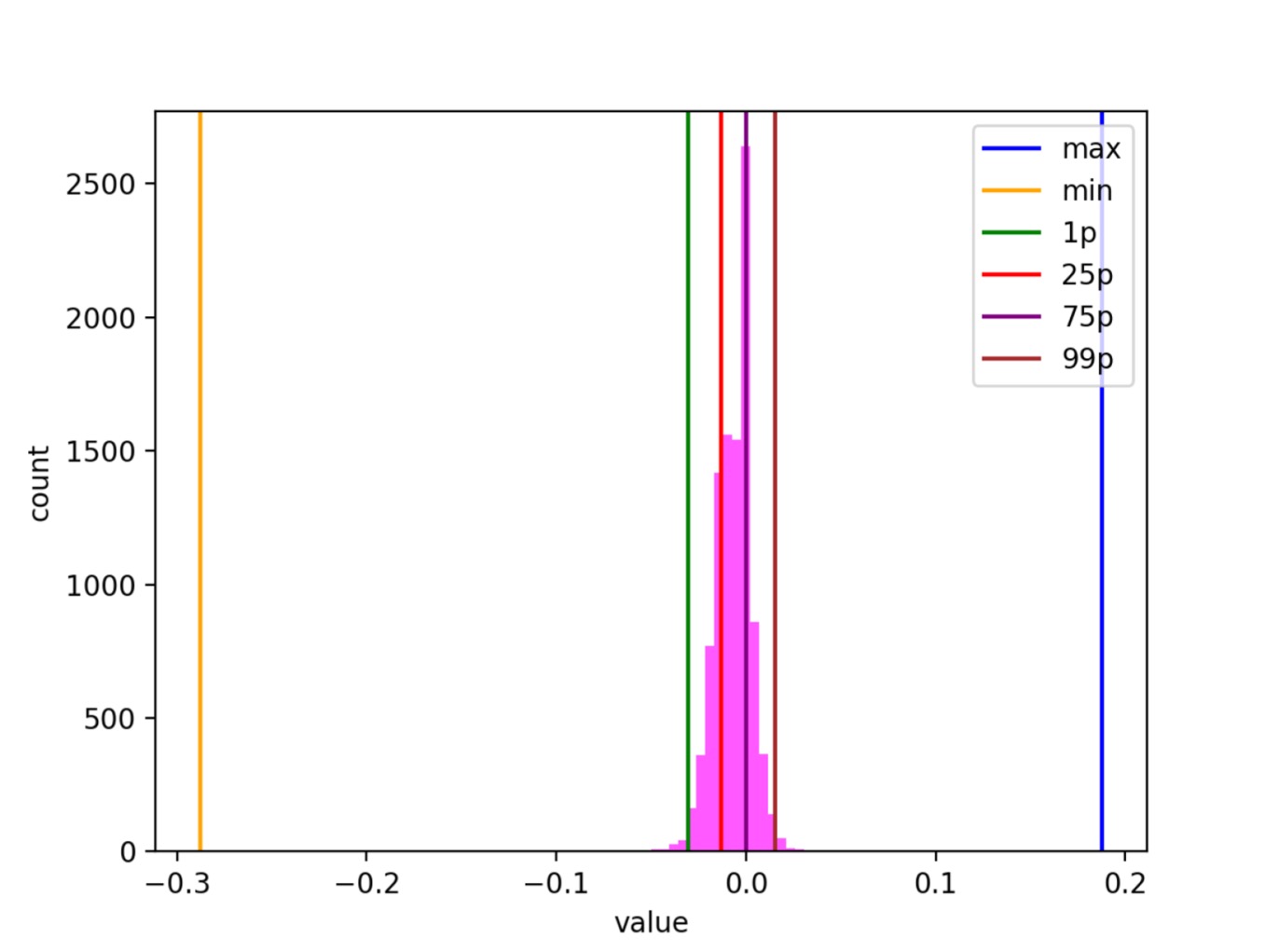
В большинстве случаев достаточно взять вместо минимумов и максимумов значения крайних перцентилей, например 1-го и 99-го. Экспериментальным путём мы выяснили, что на наших эмбеддингах можно отрезать аж до 5-го и 95-го перцентиля, не теряя качества рекомендаций. Таким образом, округлив по 1% точек с обеих сторон, получаем значительный выигрыш: сохраняем больше информации в уплотнении около нуля.
Квантование 255-quantiles
В подходе min-max мы пытались представить, что наше распределение близко к равномерному. Чем меньше оно будет похоже на равномерное, тем хуже будет работать квантование. А что, если мы сами приведём данное распределение к равномерному?
Оказывается, это совсем нетрудно. Нам нужно, чтобы отрезки в разрежённых районах были длиннее, а в густых — короче. Будем выбирать границы отрезков так, чтобы в каждый отрезок попало равное количество значений. Если бы мы хотели получить 100 отрезков, нам бы идеально подошли перцентили (1, 2, …, 99). Для 256 отрезков нам придётся брать такие перцентили: (0,389, 0,778, …, 99,611).
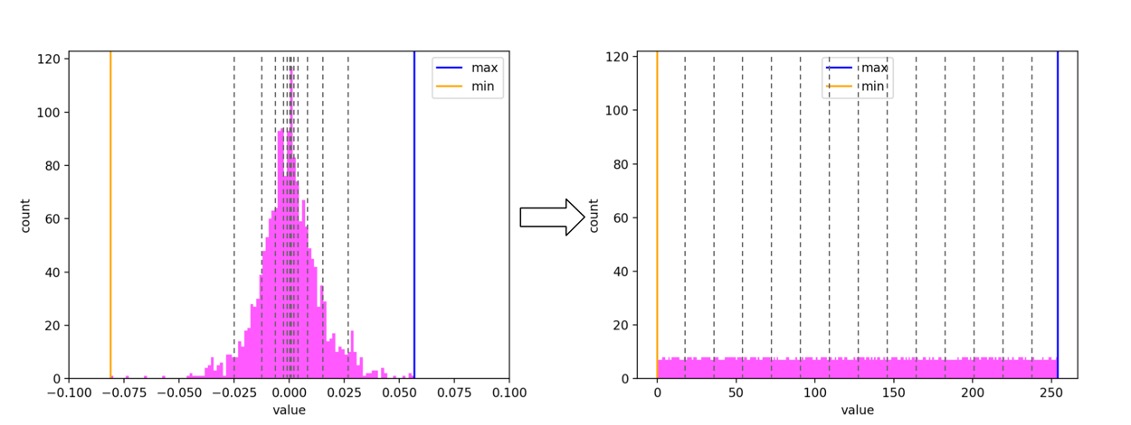
Такой алгоритм квантования сохраняет максимальное количество информации и будет одинаково хорошо работать на любом исходном распределении.
Реализовать его тоже нетрудно:
- предварительно вычисляем по семплу эмбеддингов границы интервалов (квантили);
- квантование: для каждого значения эмбеддинга находим соответствующий интервал. Это можно сделать бинарным поиском, но на практике может оказаться, что простой перебор интервалов по возрастанию будет эффективнее;
- расквантование: по индексу отрезка восстанавливаем его центр. Это просто одно чтение по индексу из массива.
Хранить при таком подходе нам нужно существенно больше информации. Для каждого индекса эмбеддинга нужно хранить все отрезки — массив из 257 элементов. Умножаем на 100 (размер эмбеддинга) и на 4 (байта во float). Всего около 100 KБ на тип эмбеддинга. Всё ещё несущественно для современных машин.
Квантование attached-extremum
Хранить дополнительные данные о структуре эмбеддингов может оказаться неудобно. Это может быть связано, например, с трудностями версионирования и синхронизации эмбеддингов. Или со сложностями интеграции с другими сервисами (например, квантовать в одном сервисе, а расквантовывать в другом).
В таком случае стоит обратить внимание на алгоритм квантования attached-extremum:
- Возьмём один произвольный эмбеддинг.
- Найдём максимум по модулю по всем индексам — назовём extr. Значения на всех индексах лежат в интервале [–extr; extr].
- Разбиваем интервал [–extr; extr] на 256 равных отрезков и берём индекс отрезка в качестве квантованного значения (как в подходе min-max).
- Значение extr отправляем/сохраняем вместе с эмбеддингом.
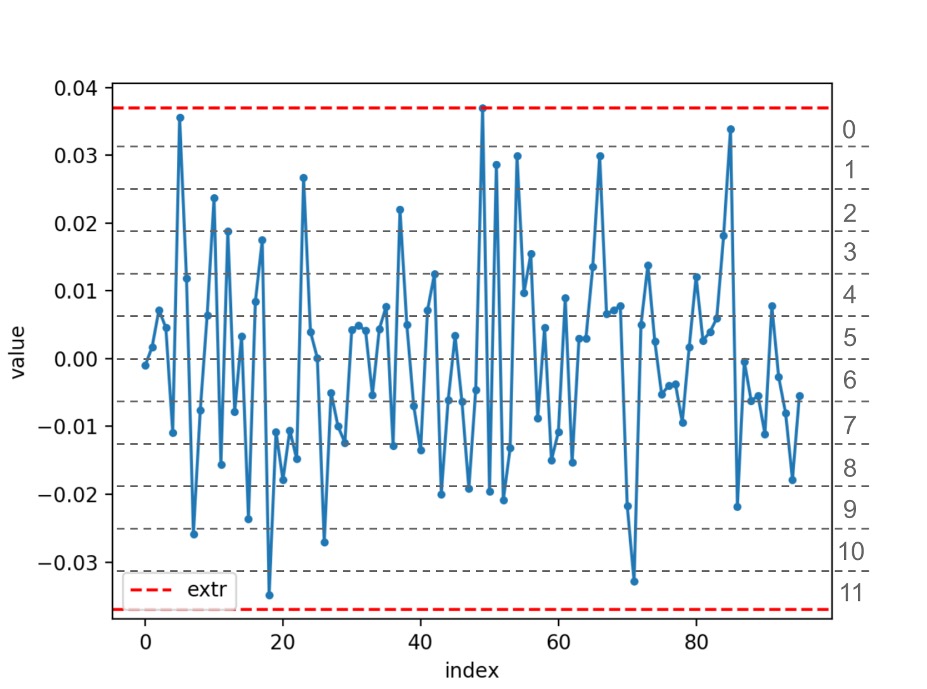
Важно обратить внимание, что у каждого эмбеддинга будет свой extr в отличие от подхода min-max, где значения min и max — общие для всех эмбеддингов одного типа.
Формулы квантования и расквантования легко получаются из min-max-формул подстановкой extr и –extr вместо max и min.

Предположения, которые должны выполняться, чтобы такой метод квантования работал хорошо:
- распределения по индексам в эмбеддинге примерно одинаковые (если на индексе i значения попадают в интервал [–100; 100], а на i + 1 — в интервал [–1; 1], то почти все значения на индексе i + 1 мы потеряем);
- значения эмбеддингов на всех индексах расположены в окрестности 0 (если будут на интервале [99,9; 100,0], то все попадут в один интервал).
Как выбрать?
Выбирая способ квантования, стоит учесть:
- распределения значений эмбеддингов (для квантования 255-quantiles нет никаких требований, для квантования attached-extremum требования самые строгие);
- вычислительные мощности (подход 255-quantiles может быть существенно тяжелее);
- динамику эмбеддингов (изменение распределений эмбеддингов внутри индексов влияет на квантование 255-quantiles сильнее, чем на другие подходы);
- хранение дополнительных данных об эмбеддингах (для квантования attached-extremum ничего хранить не нужно).
Мы проводили офлайн- и рантайм-эксперименты с этими тремя видами квантования. В офлайне сравнивали по таким критериям, как доля совпадения топа рекомендационных карточек, среднеквадратическая ошибка рекомендационного скора и т. п. В рантайме сравнивали по ключевым метрикам Яндекс.Дзена в А/Б-экспериментах.
Мы выбрали подход min-max с усечением 1-го и 99-го перцентилей. По влиянию на качество рекомендаций он несущественно отстаёт от подхода 255-quantiles. Однако 255-quantiles совершенно неприменим в нашем случае для квантования эмбеддингов карточек, так как на один запрос пользователя нам нужно расквантовать несколько десятков тысяч таких эмбеддингов. Читать элемент массива по индексу на каждый индекс каждого эмбеддинга слишком дорого. С подходом min-max эта проблема решается довольно красиво. Для вычисления скалярного произведения эмбеддинга пользователя на эмбеддинг карточки мы можем вообще не расквантовывать эмбеддинг карточки (с attached-extremum такой трюк не проходит из-за того, что у каждого эмбеддинга свой extr).
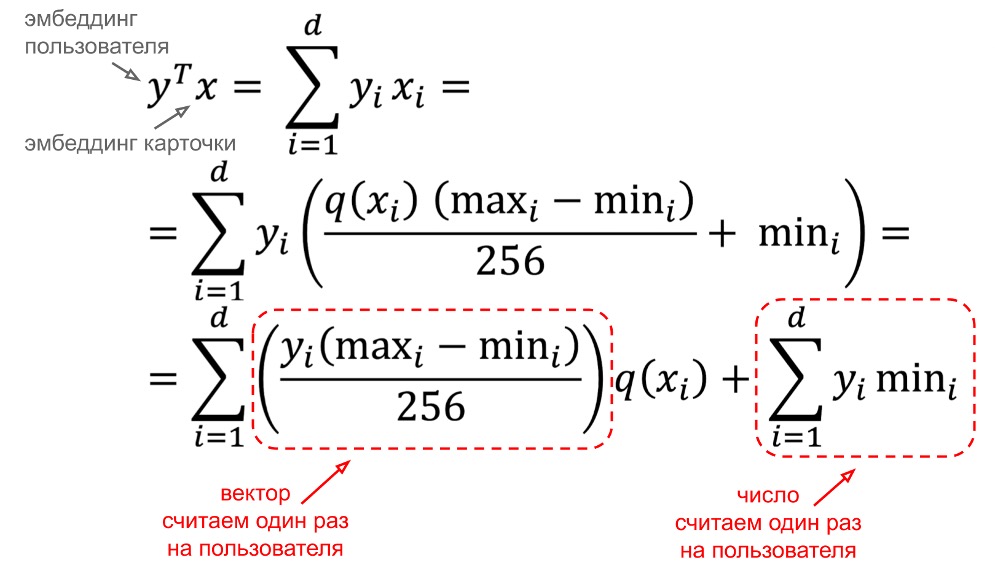
Какой профит?
При неизменившемся качестве рекомендаций мы уменьшили в четыре раза используемую память, в четыре раза сократили сетевой трафик на эмбеддинги пользователей и в четыре же раза снизили рейт записи эмбеддингов в WAL-журналы на SSD внутри нашего in-memory хранилища эмбеддингов.
Оптимизация этих узких (в плане потребления дорогих ресурсов) мест позволила нам вычислять в четыре раза больше разных типов эмбеддингов и быстрее экспериментировать с новыми их разновидностями. Что, в свою очередь, позволит Яндекс.Дзену иметь более разностороннее и глубокое представление об интересах пользователей для расчёта более точных персональных рекомендаций.
