Кустарная Колыбель Ньютона
Здравствуй, дорогой читатель! Я уже написал первую статью с самыми основами Box2D в Eclipse на Java. Сегодня на примере Колыбели Ньютона покажу, как настроить связь объектов в этой чудесной физической библиотеке.
Что же мы ожидаем увидеть?

Рисунок 1. Слишком хорошо!
Определенно, что-то, абсолютно не похожее на это!
По подключению libGDX смотрите первую статью.
Состав проекта не изменился:
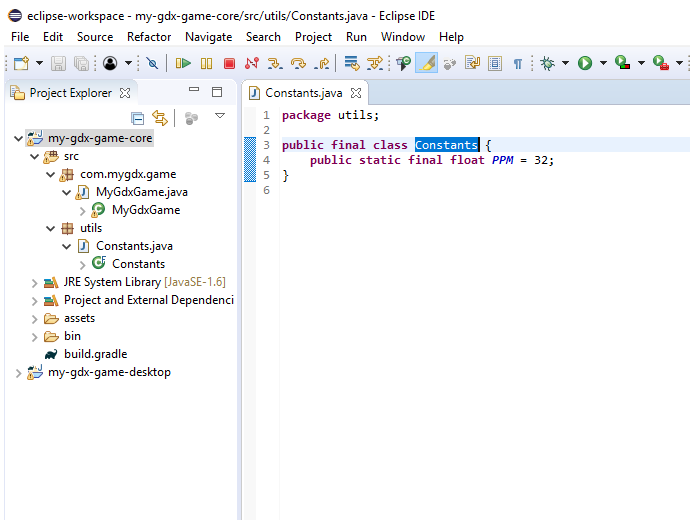
Рисунок 2. Проект. Папки и пакеты.
Я добавил в папку Core пакет Utils с классом Constants, в котором содержится только одна константа — к-во пикселей в метре. Это для того, чтобы мир не был гигантским.
Вот код для класса DesktopLauncher из пакета com.mygdx.game.desktop:
package com.mygdx.game.desktop;
import com.badlogic.gdx.backends.lwjgl.LwjglApplication;
import com.badlogic.gdx.backends.lwjgl.LwjglApplicationConfiguration;
import com.mygdx.game.MyGdxGame;
public class DesktopLauncher {
public static void main(String[] arg) {
LwjglApplicationConfiguration config = new LwjglApplicationConfiguration();
// ширина окна
config.width = 720;
// высота окна
config.height = 480;
config.backgroundFPS = 60;
config.foregroundFPS = 60;
new LwjglApplication(new MyGdxGame(), config);
}
}
В нашей физической модели первостепенное значение будет иметь коэффициент упругости. Чем он выше, тем больше колебаний совершит маятник. В Box2D параметр restitution у FixtureDef может принимать значения от 0 до 1.0f, где 0 — абсолютно не упругое тело, а 1.0f — абсолютно упругое. Лучшая модель Колыбели Ньютона у меня получилось при restitution = 0.8f:
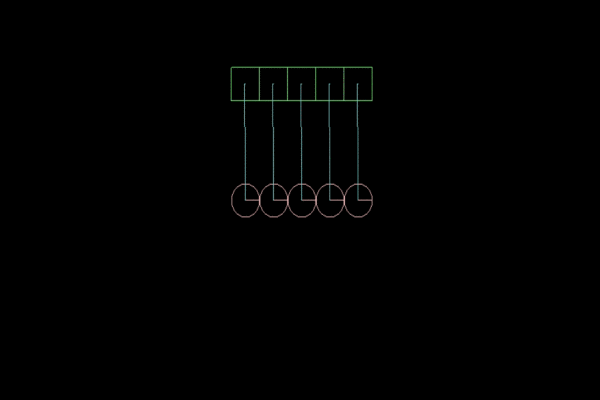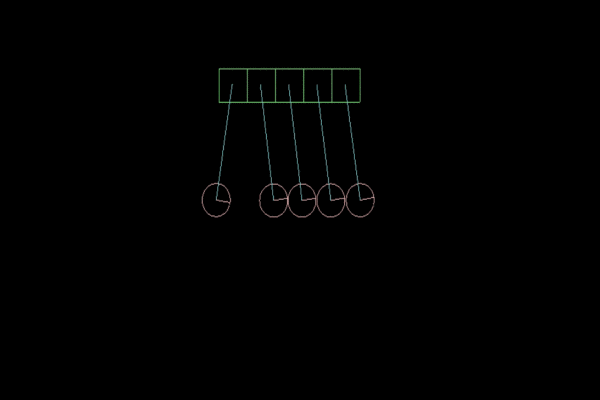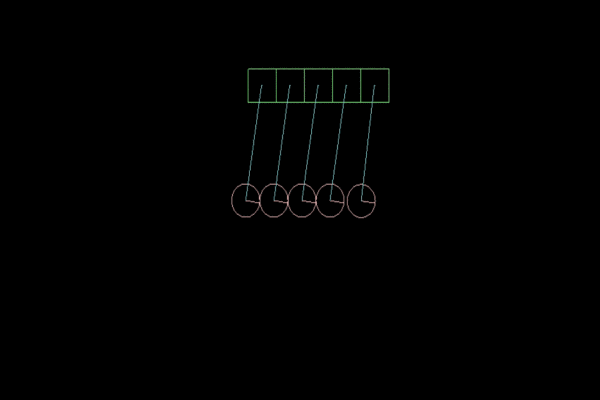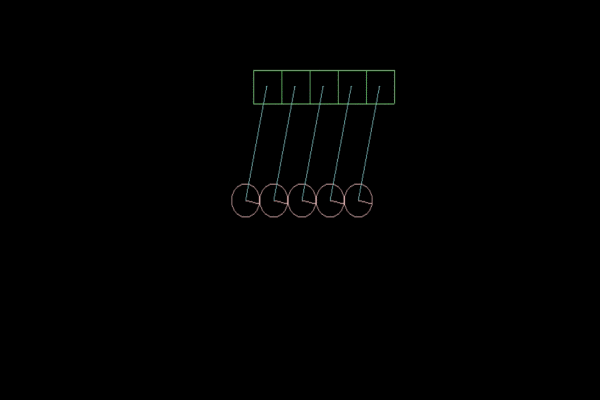
Рисунок 3. Коэффициент упругости = 0.8f, для большей наглядности замедленная съемка.
package com.mygdx.game;
import com.badlogic.gdx.ApplicationAdapter;
import com.badlogic.gdx.Gdx;
import com.badlogic.gdx.Input.Keys;
import com.badlogic.gdx.graphics.GL20;
import com.badlogic.gdx.graphics.OrthographicCamera;
import com.badlogic.gdx.math.Vector2;
import com.badlogic.gdx.math.Vector3;
import com.badlogic.gdx.physics.box2d.Body;
import com.badlogic.gdx.physics.box2d.BodyDef;
import com.badlogic.gdx.physics.box2d.Box2DDebugRenderer;
import com.badlogic.gdx.physics.box2d.CircleShape;
import com.badlogic.gdx.physics.box2d.FixtureDef;
import com.badlogic.gdx.physics.box2d.PolygonShape;
import com.badlogic.gdx.physics.box2d.World;
import com.badlogic.gdx.physics.box2d.joints.RevoluteJointDef;
import utils.Constants;
public class MyGdxGame extends ApplicationAdapter {
private OrthographicCamera camera;
private boolean DEBUG = false;
private World world;
private Body plos;
private Body plos2;
private Body plos3;
private Body plos1;
private Body plos4;
private Box2DDebugRenderer b2dr;
private Body ball;
private Body ball1;
private Body ball2;
private Body ball3;
private Body ball4;
public void create() {
float w = Gdx.graphics.getWidth();
float h = Gdx.graphics.getHeight();
camera = new OrthographicCamera();
camera.setToOrtho(false, w / 2, h / 2);
world = new World(new Vector2(0, -9.8f), false);
b2dr = new Box2DDebugRenderer();
// создаем крепления для шариков
plos = createplos(20 / Constants.PPM);
plos1 = createplos(0 / Constants.PPM);
plos2 = createplos(40 / Constants.PPM);
plos3 = createplos(80 / Constants.PPM);
plos4 = createplos(60 / Constants.PPM);
// создаем шарики
ball = createball(20 / Constants.PPM);
ball1 = createball(40 / Constants.PPM);
ball2 = createball(60 / Constants.PPM);
ball3 = createball(0 / Constants.PPM);
ball4 = createball(80 / Constants.PPM);
// связываем крепление с соответствующим ему шариком
rotation(plos, ball);
rotation(plos2, ball1);
rotation(plos1, ball3);
rotation(plos4, ball2);
rotation(plos3, ball4);
}
// здесь описывается связь шарика и крепления
public void rotation(Body body1, Body body2) {
RevoluteJointDef rjd = new RevoluteJointDef();
rjd.bodyA = body1;
rjd.bodyB = body2;
rjd.collideConnected = false;
// центр крепления для первого тела
rjd.localAnchorB.set((plos.getPosition().x) / Constants.PPM, plos.getPosition().y / Constants.PPM + 2);
// центр крепления для второго тела
rjd.localAnchorA.set((plos.getPosition().y - 6.8f) / Constants.PPM, plos.getPosition().x / Constants.PPM);
world.createJoint(rjd);
}
public void render() {
update(Gdx.graphics.getDeltaTime());
Gdx.gl.glClearColor(0, 0, 0, 1);
Gdx.gl.glClear(GL20.GL_COLOR_BUFFER_BIT);
b2dr.render(world, camera.combined.scl(Constants.PPM));
}
public void resize(int width, int height) {
camera.setToOrtho(false, width / 2, height / 2);
}
public void dispose() {
world.dispose();
b2dr.dispose();
}
public void update(float delta) {
world.step(1 / 60f, 6, 2);
cameraUpdate(delta);
inputUpdate(delta);
}
public void inputUpdate(float delta) {
// по нажатию на пробел, крайнему левому шарику сообщается скорость -7 м/с по x, -7 м/с по y
if (Gdx.input.isKeyPressed(Keys.SPACE)) {
ball3.setLinearVelocity(-7, -7);
}
}
// камера следует за центральным шариком
public void cameraUpdate(float delta) {
Vector3 position = camera.position;
position.x = ball1.getPosition().x * Constants.PPM;
position.y = ball1.getPosition().y * Constants.PPM;
camera.position.set(position);
camera.update();
}
// создание крепления
public Body createplos(float xo) {
PolygonShape shape = new PolygonShape();
Body fBody;
BodyDef def = new BodyDef();
def.type = BodyDef.BodyType.StaticBody;
def.position.set(xo, 200 / Constants.PPM);
def.fixedRotation = true;
fBody = world.createBody(def);
shape.setAsBox(10 / Constants.PPM, 10 / Constants.PPM);
fBody.createFixture(shape, 0.001f);
shape.dispose();
return fBody;
}
// создание шарика
public Body createball(float xo) {
Body pBody;
BodyDef def = new BodyDef();
def.type = BodyDef.BodyType.DynamicBody;
def.position.set(xo, 100 / Constants.PPM);
def.fixedRotation = false;
pBody = world.createBody(def);
CircleShape shape = new CircleShape();
shape.setRadius(10 / Constants.PPM);
pBody.createFixture(shape, 0.0001f);
def.bullet = true;
FixtureDef fd = new FixtureDef();
// коэффициент упругости
fd.restitution = 0.8f;
// плотность
fd.density = 10.0f;
// коэффициент трения
fd.friction = 0f;
fd.shape = shape;
pBody.createFixture(fd);
shape.dispose();
return pBody;
}
}
Вы можете самостоятельно изменять коэффициенты и получать различные результаты. Кроме того, на примитивы можно наложить текстуры для достижения большей реалистичности.
Далее будут представлены gif-изображения для различных значений коэффициента упругости.
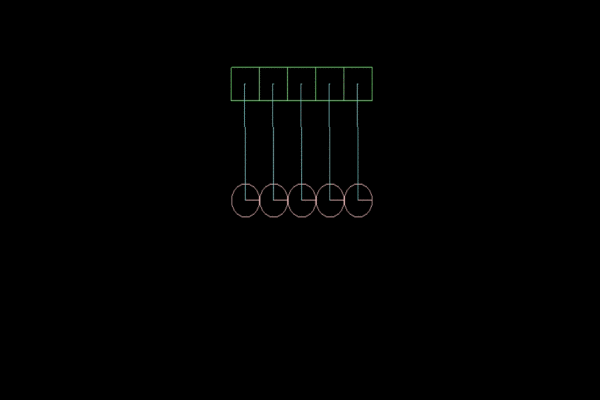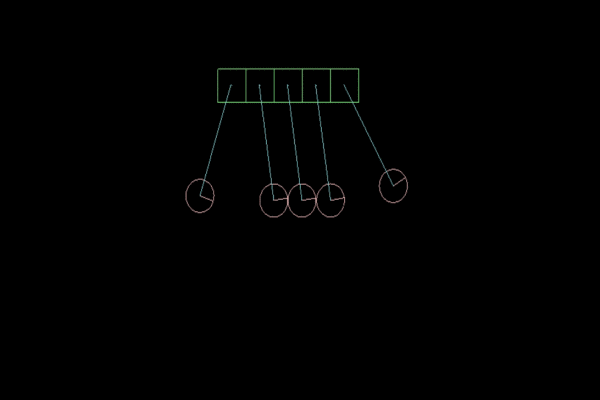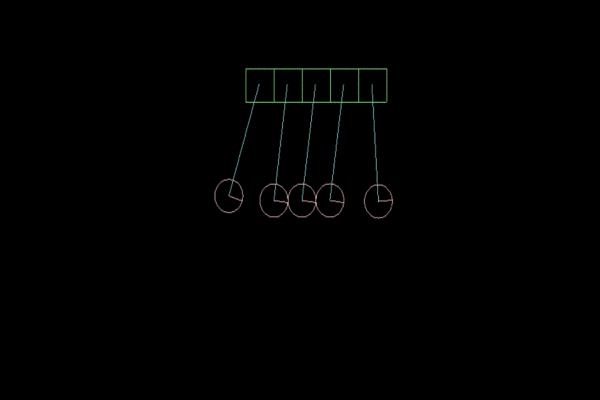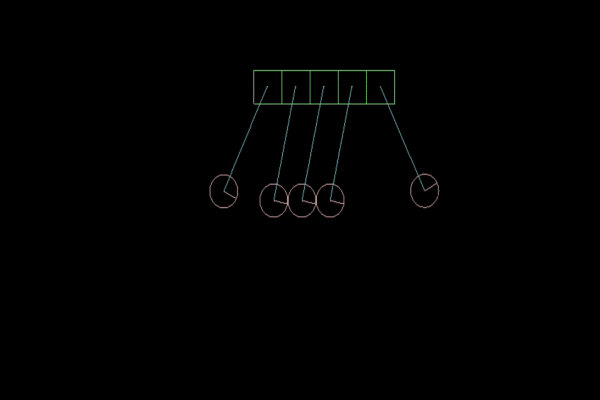
Рисунок 4. Коэффициент упругости, равный 1f.

Рисунок 5. Коэффициент упругости, равный 0.5f.

Рисунок 6. Коэффициент упругости, равный 0.2f.

Рисунок 7. Коэффициент упругости, равный 0.
Идей много, стараюсь выкладывать результаты по мере возможности! Спасибо, что прочли до конца, надеюсь, статья была полезной для вас! Давайте вместе устроим настоящий хаос в игровом мире благодаря библиотеке Box2D!
P.S. Отвечу на все вопросы в комментариях.
