Криптография на основе эллиптических кривых в TLS 1.307.11.2019 10:19

Пара предупреждений читателю:

Для того, чтобы (насколько это возможно) упростить процесс объяснения и сжать объем публикации, стоит сразу же сделать ключевую оговорку — все, что мы пишем, касаемо практической стороны рассматриваемой проблематики, корректно для протокола TLS версии 1.3. Это значит, что хотя ваш ECDSA сертификат и будет, при желании, работать с TLS 1.2, описание процесса хендшейка, наборов шифров и бенчмарков сделано на основании последней версии протокола TLS — 1.3. Как вы понимаете, это не относится к математическому описанию алгоритмов, лежащих в фундаменте современных криптографических систем.

Данный материал был написан не математиком и даже не инженером — хотя они и помогали проложить дорожку сквозь математические дебри. Огромная благодарность сотрудникам Qrator Labs.

(Elliptic Curve) Diffie-Hellman (Ephemeral)

Наследие Диффи — Хеллмана в XXI веке

Естественным образом, данная тема начинается не с Уитфилда Диффи и не с Мартина Хеллмана. Алан Тьюринг и Клод Шеннон сделали огромный вклад в теорию алгоритмов и теорию информации, равно как и в область криптоанализа. Диффи и Хеллман, в свою очередь, официально признаются авторами идеи криптографии с публичным ключом (также называемой асимметричной) — хотя теперь известно, что в Великобритании были также достигнуты серьезные результаты в этой области. Однако они оставались засекреченными длительное время — что делает двух джентльменов, упомянутых в подзаголовке, первопроходцами.

В чем именно?
Это может показаться забавным, однако до 6 ноября 1976 года не существовало доступных знаний относительно криптографических систем с открытым ключом. Уитфилд Диффи и Мартин Хеллман (и, фактически, Ральф Меркл) — математики, компьютерные инженеры и энтузиасты, а также криптологи были первыми, кто предложил подходящую концепцию.

Из-за той особенной роли, которую занял криптоанализ во время Второй Мировой войны и несоизмеримым его влиянием на способность держать информацию в тайне, две страны, считавшие, что обладают наиболее продвинутыми знаниями в области криптографии — Соединенные Штаты Америки и Соединенное Королевство — включили криптографические алгоритмы в раздел вооружений, наложив вето на их экспорт (одновременно с этим ослабив доступные и предназначенные для коммерческого или домашнего использования реализации). Именно по этой причине британские исследователи, работавшие над асимметричной схемой распределения ключей в Центре правительственной связи (GCHQ) и разработавшие аналогичную концепцию не были признаны сообществом вплоть до 1997 года, когда существовавшие ограничения на криптографические алгоритмы и их описание утратили всякий смысл и, по большому счету, морально устарели.

Возвращаясь назад к нашей паре изобретателей — что именно революционизировали Диффи с Хеллманом?

Для объяснения этого давайте взглянем на иллюстрацию из оригинальной публикации, отлично отражающую гигантский прыжок в понимании того, как может работать криптография — пусть даже изначально только теоретически: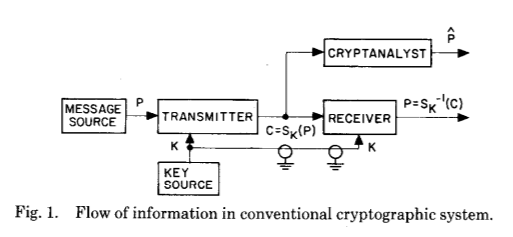

А теперь на следующую: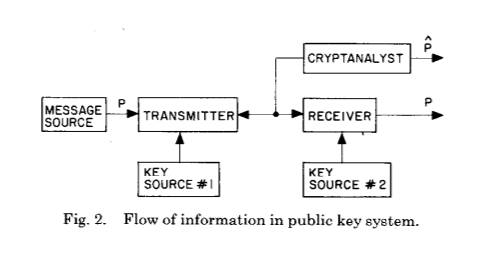

Две эти картинки показывают главное нововведение Уитфилда Диффи и Мартина Хеллмана спустя столетия развития криптографии и криптоанализа — установление общего секрета в результате вычислений определенного типа.

Давайте посмотрим на еще одну картинку из Википедии, где в роли секретов используются различные цвета:

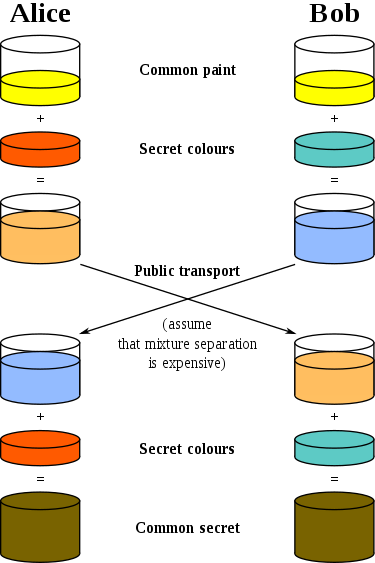
Она также хорошо объясняет, что происходит. До инновации Диффи и Хеллмана в виде схемы установления общего ключа существовал лишь один общий ключ — он использовался для зашифрования и расшифрования сообщения. Если вы хотите передать такой ключ второй стороне — он должен быть передан по изначально защищенному каналу. Сразу же становятся ясны все ограничения такой схемы — вам необходим надежно защищенный (от прослушивания) канал связи, вы не можете использовать один и тот же ключ более одного раза, и, в идеале, длина ключа должна соответствовать длине сообщения.

Клод Шеннон в своей позже рассекреченной работе «Теория связи в секретных системах» доказал, что все теоретически невзламываемые шифры должны обладать теми же свойствами, что и одноразовый шифроблокнот — также известный как шифр Вернама, по имени создателя этого аддитивного полиалфавитного поточного алгоритма шифрования.

И снова давайте взглянем на оригинальную научную публикацию: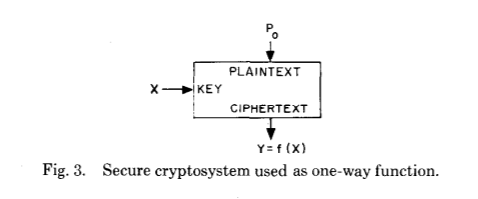

Прежде чем мы пойдем дальше, давайте зададим себе очевидно простой вопрос — каким образом два, пусть даже очень интеллектуально развитых, человека смогли придумать нечто настолько прорывное в прикладном поле, особенно учитывая огромные успехи военного времени? Скорее всего из-за совокупности следующих активно развивавшихся тогда областей:

Можно сказать, что все эти области развились и заматерели примерно в один и тот же период 20-го века. Диффи и Хеллман также упоминали Клода Шеннона как фигуру, повлиявшую на их работу больше остальных.

Концепт «Универсальной безопасности» Арьена Ленстры показывает, сколько энергии необходимо потратить на «взлом» симметричной криптосистемы с ключами разной длины. Оказалось, что для взлома 228-битного ключа к алгоритму на основе эллиптических кривых понадобится энергии столько, сколько достаточно для нагревания до точки кипения всей воды на Земле. Однако данное утверждение корректно, только если мы рассматриваем известные алгоритмы и используем современное оборудование, так как, строго говоря, возможны более эффективные алгоритмы или оборудование, но об их существовании пока неизвестно. 228-битный ключ к EC-алгоритму по сложности взлома сравним с 2380-битным ключом в RSA, но об этом чуть позже. В данном сравнении RSA и EC ключи используются в асимметричной криптосистеме, их можно считать эквивалентными 128-битному ключу в симметричной схеме.

Легко представить, что «сложно рассчитываемое» нечто будет требовать большое количество времени и энергии на вычисление. Мы склонны считать, что компьютеры могут «посчитать все что угодно», но оказывается, что это далеко от истины. Во-первых, существуют примеры неразрешимых задач, такие как проблема остановки. Впрочем, в области криптографии такие задачи не используются. Во-вторых, если мы рассмотрим время выполнения, необходимое определенному алгоритму, то оно может быть сколь угодно большим. Это именно то, что использует криптография. Задача считается вычислительно «простой», если время необходимое для работы соответствующего алгоритма зависит от размера входных данных (измеренного в битах) как полином: $T(n) = O(n^k)$ , для некоторого положительного $k$ . В теории сложности вычислений такие задачи образуют класс сложности P. Если же время работы алгоритма растет быстрее полинома, например, экспоненциально, то такая задача считается вычислительно «трудной».

Класс сложности P включает задачи для которых существует детерминированный алгоритм, работающий за полиномиальное время. Другим классом сложности является NP (в котором, предположительно, существуют «трудные» задачи), представляющий собой задачу разрешимости — то есть проблему, требующую ответа «да» или «нет», правильность решения которых можно проверить — то есть предъявить доказательство корректности решения — за полиномиальное время. Видите здесь слово «доказательство»? Это место, в котором мы переходим к односторонним функциям, задача обращения которых принадлежит к классу сложности NP.

Автор: xkcd

(Односторонние функции (с потайным входом))

По определению, односторонней функцией является такая функция, которую легко подсчитать для любого входа, но трудно инвертировать, то есть получить оригинальный вход имея только результат. «Легко» и «трудно» относятся к теории сложности вычислений, упомянутой выше. Интересно, что существование односторонних функций (математически) не доказано, так как строгое доказательство их существования доказало бы и неравенство классов P и NP — одной из задач тысячелетия и актуальной открытой проблемы, чье решение сулит алгоритмический прорыв. Поэтому необходимо держать в уме то, что почти вся современная криптография опирается на недоказанные гипотезы.

В своей оригинальной публикации Диффи и Хеллман вводят новое поколение односторонних функций, называя их «односторонними функциями с потайным входом» — по английски trapdoor function. Как они отличаются от просто односторонних функций?

Давайте посмотрим на их оригинальное объяснение:
В криптосистеме с публичным ключом шифрование и дешифрование осуществляется различными ключами — E и D соответственно, такими, что вычисление D от E практически неосуществимо (например, требующее $10^{100}$ инструкций). Шифрующий ключ E может быть разглашен публично без компрометации ключа D. Это позволяет любому пользователю системы отправить сообщение любому другому пользователю, зашифрованное таким способом, что только ожидаемый получатель сможет расшифровать его. <…> Задача аутентификации, пожалуй, представляет собой более серьезную проблему телекоммуникаций для бизнес-транзакций, по сравнению с распределением ключей, так как именно она (аутентификация) лежит в сердце любой системы работающей с контрактами и выставлением счетов к оплате.

Обычно для объяснения принципов работы криптосистемы используют криптографических персонажей Алису и Боба (они стремятся к защищенной коммуникации). Алиса и Боб договорились выбрать большие простые числа $n$ и $g$ , такие что $1< g< n$ . Этот выбор влияет на безопасность всей схемы. Число $n$ , называемое модулем, должно быть простым; более того, число $(n-1)/2$ тоже должно быть простым, а $g$ должно быть первообразным корнем в группе вычетов по модулю $n$ ; кроме того, $n$ должно быть достаточно большими — не менее 512 бит в двоичном представлении. Далее, протокол Диффи — Хеллмана может быть описан в пять простых шагов:

Алиса выбирает (большой простое) и вычисляет $X=g^x \bmod n$
Боб выбирает (тоже большое простое) и вычисляет $Y=g^y \bmod n$
Алиса отправляет Бобу, Боб отправляет Алисе ( и остаются у каждого из них в секрете)
Алиса вычисляет $k = Y^x \bmod n$
Боб вычисляет $k' = X^y \bmod n$

В результате Алиса и Боб получают одинаковый по построению результат $k=k'$ — общий секрет.

Итак, односторонняя функция с потайным входом это такая односторонняя функция, которую можно обратить имея кусочек специальной информации, называемой «потайным входом». Звучит просто, однако на практике найти такую функцию оказалось нетривиальной задачей — первый достойный метод оказался прародителем целого семейства алгоритмов на основе публичного ключа, названного RSA по фамилиям его создателей: Рон Ривеста, Ади Шамира и Леонарда Адлемана.

RSA

В RSA сложность инвертирования функции основывается на том факте, что факторизация (разложение числа на множители) занимает гораздо больше времени, чем умножение или, точнее, можно утверждать, что не найдено метода факторизации больших чисел за полиномиальное время на классическом компьютере, хотя и не было доказано, что такого алгоритма не может существовать.

В RSA, как и в любой другой криптографической системе с публичным ключом, есть два ключа: публичный и приватный. Алгоритм RSA берет входное сообщение, представленное битовой строкой и применяет к ней математическую операцию (возведение в степень по модулю простого числа) для того чтобы получить результат, неотличимый от случайного. Для расшифровки берется результат и производится похожая операция для получения оригинального сообщения. В асимметричной криптографии шифрование осуществляется публичным ключом, а дешифрование — приватным.

Как это возможно? Благодаря тому, что используемые значения принадлежат конечной циклической группе (множество целых чисел с умножением в модульной арифметике). Компьютеры не очень хорошо работают с произвольно большими числами, но, свойством циклической группы является «wrap around» — число, большее чем разрешенный максимум, «заворачивается» до значения из разрешенного множества. Это позволяет нам использовать ключи с длиной «не более чем» какое-то количество бит. В криптографии на основе эллиптических кривых циклические (мультипликативные) группы также используются, но конструируются несколько иначе, как мы увидим дальше.

На совсем примитивном уровне, все, что делает RSA — это берет два больших простых числа, умножая их для того чтобы получить так называемый модуль. Все остальные числа, с которыми будут производиться операции должны находится между нулем и значением модуля. Сам же модуль станет частью публичного ключа — его длина определяет и длину ключа. Вторая часть публичного ключа — это число выбранное между нулем и значением функции Эйлера (современные реализации RSA используют функцию Кармайкла вместо Эйлера) от модуля, с некоторыми дополнительными ограничениями. Наконец, можно высчитывать приватный ключ, решив модульное уравнение. Для шифрования сообщения мы берем число, представляющее сообщение, и просто возводим его в степень, равную значению публичного ключа, а для дешифрования — получения исходного сообщения — возводим его в степень, равную значению приватного ключа. Благодаря циклической природе группы, мы получим то же самое значение.

Сегодня у RSA есть две основные проблемы, причем одна является следствием другой. С ростом длины ключа сложность растет не настолько быстро, как хотелось бы. Это происходит потому, что существует субэкспоненциальный (но все еще сверхполиномиальный) алгоритм факторизации. Поэтому, для поддержания необходимого уровня защиты, длина RSA ключа должна расти несколько быстрее, чем у ECC ключа. По этой причине наиболее распространенные сегодня длины ключей RSA является довольно большими: 2048 и 3072 бит.

Чуть позже увидим на конкретных цифрах, как длина ключа влияет на конечную производительность криптосистемы, сравнив подписанные у Let«s Encrypt RSA и ECDSA сертификаты.

Elliptic Curve Digital Signature Algorithms

В поисках более надежных функций с потайным входом, в середине 80-х годов криптографы пришли к задействованию ветви математики, посвященной эллиптическим кривым.

Было бы слишком сложно описать все детали криптографии на основе эллиптических кривых в одном тексте, поэтому мы не станем этого делать. Вместо этого, давайте посмотрим на одностороннюю функцию с потайным входом, построенную на основе эллиптических кривых и задаче о дискретном логарифме.

Существует большое количество обзорных материалов и более детальных введений в данную область криптографии. Мы бы хотели особенно отметить «ECC: a gentle introduction» за авторством Андреа Корбеллини, особенно если вам интересен матаппарат.

Мы же, в данном материале заинтересованы в куда более «простом» объяснении.
Эллиптическая кривая определяется уравнением, которое выглядит следующим образом: $y^2 = x^3 + ax + b$ .

Вторым объектом является циклическая подгруппа над конечным полем. В алгоритме ECC используются следующие параметры:

В итоге, набор параметров для наших алгоритмов представляется шестеркой .

Точки эллиптической кривой принадлежат конечному полю $\mathbb{F}_p$ , где $p$ это достаточно большое простое число. Итак, у нас есть множество целых чисел по модулю $p$ , где возможны такие операции как сложение, вычитание, умножение, взятие обратного. Сложение и умножение работают схожим образом с тем, как мы это описывали в части модульной арифметики раздела RSA (wrap-around).

Так как кривая симметрична относительно оси х, для любой точки $P$ мы можем взять $−P$ и получить точку, противоположную ей. Мы сразу оговариваем, что точка $−O$ соответствует нулю, то есть $−O$ будет просто $O$ .

Сложение точек на кривой определено так, что, зная точки $P$ и $Q$ , мы можем нарисовать прямую, проходящую через обе этих точки, а также третью — $R$ , так что $P+Q=-R$ и $P+Q+R=0$ .

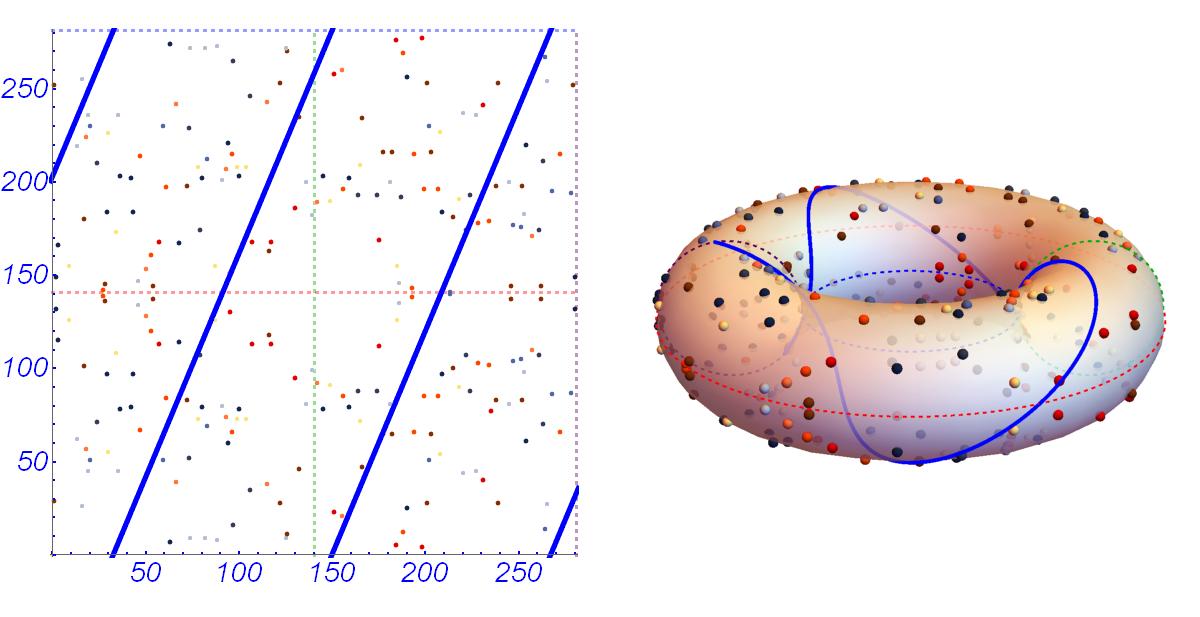
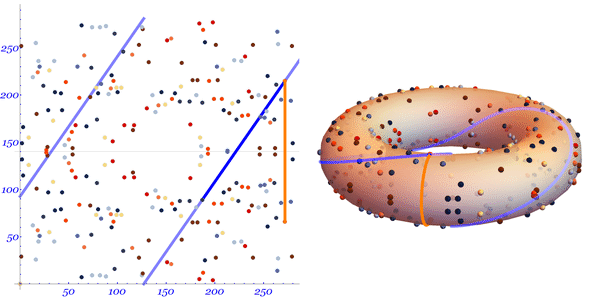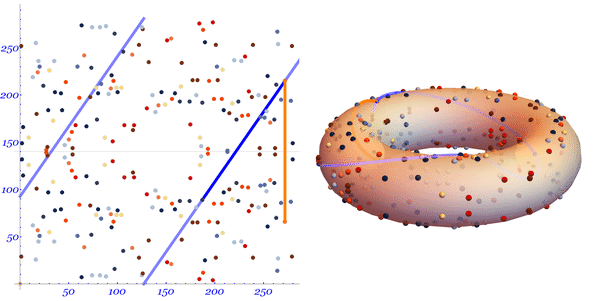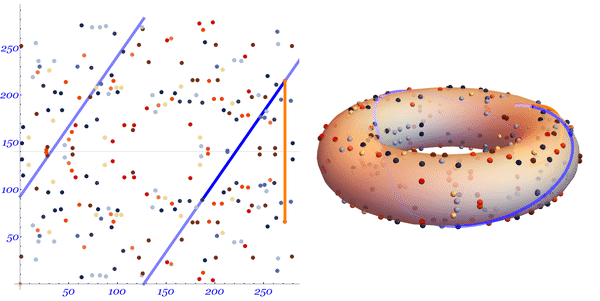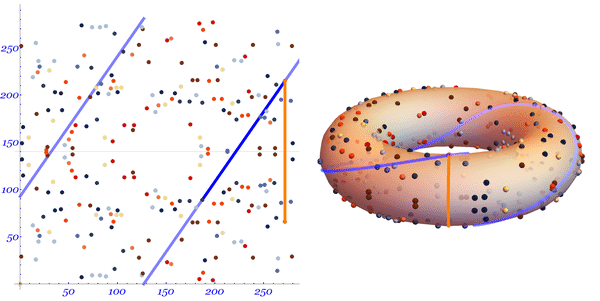
Давайте посмотрим на доступно иллюстрированное объяснение Марка Хьюза:

Мы видим прямую, протянутую по поверхности тора. Линия пересекает две произвольно выбранные точки на кривой.
Для того чтобы найти , мы рисуем прямую от первой выбранной точки ко второй , продолжая линию до тех пор, пока она не пересечет кривую в третьей точке .
После пересечения, отразим точку относительно оси абсцисс для того чтобы найти точку .

Умножение на скаляр определяется достаточно очевидно: $n\cdot P = P + P + P + \dots + P$ .

Односторонняя функция с потайным входом в данном случае опирается на задачу дискретного логарифма для эллиптических кривых, а не на факторизацию, как в случае с RSA. Проблема дискретного логарифма в данном случае формулируется так: если известны $P$ и $Q$ , то как найти $k$ , такое что $Q=k\cdot P$ ?

И задача факторизации (лежащая в основе RSA), и дискретного логарифма для эллиптических кривых (являющаяся фундаментом ECDSA и ECDH) считаются трудными — другими словами, неизвестно алгоритмов для решения этих задач за полиномиальное время при заданной длине ключа.

Хотя, обычно, меня бы забросали грязными (в лучшем случае) тряпками за смешивание алгоритмов распределения ключа (ECDH) с подписью (ECDSA), мне все таки придется объяснить, как они работают вместе. Современный TLS-сертификат содержит публичный ключ, в нашем случае, от пары сгенерированной с помощью алгоритма на основе эллиптических кривых, обычно подписанный какой-то авторитетной организацией. Клиент проверяет подпись сервера и генерирует общий секрет. Этот секрет используется в симметричном алгоритме шифрования, например AES или ChaCha20. Тем не менее, базовые принципы остаются теми же: согласовать набор (шестерку) параметров, получить пару ключей, где приватный ключ — это случайно выбранное целое число (множитель от $Q=k\cdot P$ ), а публичный ключ — это точка на кривой. Алгоритмы подписи используют базовую точку $G$ , которая является генератором подгруппы порядка $n$ ( $n$ — большое простое число), так что $n\cdot G=0$ , где 0 — это нейтральный элемент группы. Подпись доказывает, что защищенное соединение устанавливается с аутентифицированной стороной — сервером, который обладает TLS сертификатом (публичным ключем) подписанным авторитетной организацией для заданного имени сервера.

(EC)DH (E)+ECDSA = Современная форма хендшейка

В современном TLS версии 1.3 клиент и сервер генерируют пару ключей на лету, устанавливая соединение. Это называется «эфемерной» версией алгоритма обмена ключей. Наиболее популярные TLS библиотеки поддерживают именно такую версию протокола. В большинстве своем, сегодня используется эдвардсовская эллиптическая кривая 25519, предложенная Дэниэлом Бернштайном младшим (djb), которая предоставляет 128-битный уровень защиты. С 2014 года эта кривая доступна для создания пары ключей в библиотеке openssh. Однако, по состоянию на конец 2019 года, браузеры все еще не устанавливают TLS-сессию с серверами, использующими публичный ключ к алгоритму подписи EdDSA.

Давайте рассмотрим, как все работает в TLS 1.3.

В последней на текущей момент версии протокола механизмы распространения ключа ограничены до основанных на (EC)DH (E) — x25519 является наиболее распространенной функцией для получения общего ключа — именно она поддерживается большинством браузерных и серверных TLS-библиотек. Набор шифров состоит только из трех записей: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 и TLS_CHACHA20_POLY1305_SHA256. Для тех из вас, кто знаком с тем, как были поименованы наборы шифров в предыдущей версии протокола — TLS 1.2, очевидно, что указание на механизм обмена ключа было «отделено» от набора шифров при переходе к TLS 1.3. Также из спецификации были выброшены статические способы обмена ключа RSA и DH. Даже восстановление сессии в TLS 1.3 с помощью PSK и тикетов предыдущей сессии происходит по протоколу ECDHE, где особенно важно последнее E — эфемерность. Также в TLS 1.3 отсутствует возможность задавать собственные значения для механизма Диффи — Хеллмана — в спецификациях протокола оставлен только предустановленный набор, в отношении безопасности которого есть консенсус.

Отдельный интерес представляет собой тот факт, что современные асимметричные механизмы шифрования работают по-разному. В ECC (в частности, при использовании ECDSA сертификатов) мы используем ключи относительно небольшой длины, по сравнению с RSA, для того чтобы добраться до приемлемых уровней безопасности. Это позволяет использовать сильную асимметричную криптографию и схемы обмена ключей даже на таких устройствах, которым, казалось бы, не должно хватать мощности на необходимые операции — например, смарт-картах.

Во-первых, необходимо уточнить, что значит термин «гибридная криптосистема» применимо к описанию TLS 1.3. Гибридная криптосистема использует асимметричную (с публичным ключом) схему шифрования для установления общего секрета, который далее используется в качестве ключа в симметричном блочном или поточном алгоритме шифрования.

Во-вторых, существует инфраструктура публичных ключей (PKI) и сертификатов (CA). Занятно, что в 2004 году Мартин Хеллман упомянул одного из «невоспетых героев» — Лорена Кёнфельдера, чьим тезисом на защите диплома бакалавра MIT была возможность создания древовидной структуры — того, что мы и знаем сегодня как PKI. Но давайте вернемся к сертификатам.

Тот факт, что сервер действительно владеет приватным ключом, удостоверяется его подписью, которая может быть проверена с помощью публичного ключа. А файл сертификата на сервере удостоверяет, что определенный публичный ключ принадлежит определенному серверу. Это значит, что вы устанавливаете защищенное соединение с желаемым собеседником, а не самозванцем — вашим банком, а не кибермошенником.

В TLS 1.3 произошло значительно улучшение схемы согласования по сравнению с предыдущими версиями протокола. Теперь сервер подписывает всю информацию, полученную в хендшейке к моменту создания такой подписи: client hello и собственный server hello вместе с набором шифров, выбранным для использования. Давайте взглянем на соответствующую секцию описания взаимодействия из RFC 8446:

       Client                                           Server

Key  ^ ClientHello
Exch | + key_share*
     | + signature_algorithms*
     | + psk_key_exchange_modes*
     v + pre_shared_key*       -------->
                                                  ServerHello  ^ Key
                                                 + key_share*  | Exch
                                            + pre_shared_key*  v
                                        {EncryptedExtensions}  ^  Server
                                        {CertificateRequest*}  v  Params
                                               {Certificate*}  ^
                                         {CertificateVerify*}  | Auth
                                                   {Finished}  v
                               <--------  [Application Data*]
     ^ {Certificate*}
Auth | {CertificateVerify*}
     v {Finished}              -------->
       [Application Data]      <------->  [Application Data]

В TLS 1.3 клиент отправляет свою часть ключа (вместе с необходимыми параметрами) и перечень доступных алгоритмом подписи в первом сообщении (Client Hello). Необходимые на данном этапе ключи создаются клиентом на лету — пользователь даже не замечает этого. Далее клиент и сервер обмениваются этой информацией для создания общего секрета — сессионного ключа, который создается (или, точнее, является производным) от пре-мастер пары, полученной после того, как сервер ответил клиенту своим сообщением (Server Hello).
На стороне «Server Hello» можно увидеть запись, соответствующую передаче сертификата клиенту (Certificate*), вместе с проверкой CertificateVerify*, удостоверяющей что у стороны действительно имеется приватный ключ, относящийся к соответствующей записи публичного ключа, далее создавая сессионную (симметричную) пару ключей в случае успеха. Другими словами, запрашивающая данные стороны (клиент) успешно проверила аутентичность отвечающей стороны (сервера), перейдя к использованию общего секрета.

Две основные криптографические операции зашиты в этой пересылке — создание подписи и проверка подписи. Эти операции обычно выполняются на разных концах соединения, так как чаще всего клиенты проверяют аутентичность сервера. Подпись по сути представляет собой подтверждение владения приватным ключом, соответствующего ключу публичному. То есть, что мы получаем данные от именно подписанта, и удостоверяемся что сообщение не было изменено при передаче.

При использовании алгоритма RSA, как мы продемонстрируем чуть позже на цифрах, операция создания подписи получается самой дорогой. Так как мы подписываем 2048 или 3072-битным ключом, такая операция значительно нагружает сервер — куда сильнее, чем клиента при ее (подписи) проверке.

В ECDSA мы оперируем сравнительно короткими ключами (в примере с бенчмарками мы посмотрим на ECDSA с использованием кривой NIST P-256 (или secp256v1), но эти ключи задействованы в более сложных операциях. В результате использование ECC может быть представлено как «перевернутый» RSA с точки зрения производительности: клиент нагружается значительно сильнее операцией проверки подписи, в то время как сервер с легкостью справляется с операцией создания подписи. Это подтверждается замерами, которые мы приводим в секции бенчмарков.

Этот эффект способствует масштабированию интернета — так как современные клиенты почти настолько же мощны, как и серверы (если рассматривать только тактовую частоту работы процессорного ядра), они могут эффективно взять на себя вычислительно трудную операцию без проблем. Сервер же, в свою очередь, может использовать освободившуюся вычислительную мощность для создания большего количества подписей и, в итоге, установления большего количества сессий.

Подпись сертификата у Let«s Encrypt

Предоставим нашему читателю простую и понятную инструкцию, по которой можно самостоятельно создать способный к установлению TLS-сессии сервер с использованием пары ключей ECDSA, в которой публичный подписан Let«s Encrypt и включен в виде сертификата в цепочку доверия.
Мы решили показать полный путь от создания ключей, создания запроса на подпись сертификата (CSR) для Let«s Encrypt и его передачу на подпись с помощью утилиты certbot, возвращающей нам необходимые цепочки и сам ECDSA сертификат.

Для начала требуется создать пару ключей. Для этого мы будем использовать библиотеку OpenSSL. Руководство пользователя OpenSSL говорит, что создание ключей к алгоритмам на основе эллиптических кривых происходит с помощью специальной команды, выделенной для семейства алгоритмов на основе эллиптических кривых.

openssl ecparam -genkey -name -secp256v1 -out privatekey.pem

Для проверки, что наша команда отработала корректно, мы выполняем команду ec указывая путь ко вновь созданному файлу содержащему приватный ключ.

openssl ec -in privatekey.pem -noout -text

Вывод должен показать нам используемую кривую, с помощью которой был сгенерирован ключ.

Следующий этап достаточно важен при создании CSR — для того чтобы каждый раз не заполнять анкету, необходимую для подписи сертификата, нам нужен конфигурационный файл. К счастью, почти всю работу за нас сделала Mozilla, создав «SSL Configuration Generator». В нем можно выбрать из множества опций режимов работы сервера, с которым можно установить TLS-соединение. Чистый конфиг OpenSSL, по какой-то причине отсутствующий в генераторе Mozilla, выглядит следующим образом:

[ req ]
prompt = no
encrypt_key = no
default_md = sha256
distinguished_name = dname
req_extensions = reqext

[ dname ]
CN = example.com
emailAddress = admin@example.com

[ reqext ]
subjectAltName = DNS:example.com, DNS:*.example.com

Примечание: вам не обязательно иметь конфигурационный файл — если его нет, вам будет предложено заполнить все поля в командной строке. С конфигурационным файлом, путь к которому мы задаем в следующей команде, процесс упрощается.

Далее следует создание самого запроса на подпись сертификата (CSR). Для этого у нас есть удобная команда OpenSSL.

openssl req -new -config -pathtoconfigfile.cnf  -key privatekey.pem -out csr.pem

Мы также можем проверить корректность вновь созданного CSR.

openssl req -in csr.pem -noout -text -verify

Наконец, мы подходим к финальному этапу — используя ACME клиент, certbot, передадим наш запрос на подпись сертификата организации Let«s Encrypt.

Certbot поможет не только получить сертификат, но и обладает множеством других замечательных опций. Добавим, что если вы новичок в области криптографии с публичным ключем и не очень понимаете инфраструктуру публичных ключей существующую на текущий момент, лучше используйте опцию --dry-run перед тем как попытаетесь получить настоящий сертификат для любого из своих доменов.

certbot certonly --dry-run --dns-somednsprovider --domain "example.com” --domain "*.example.com” --csr csr.pem

В данном случае, клиент certbot проверяет, что запрашиваемый в командной строке список необходимых доменов соответствует списку в запросе на подпись сертификата (CSR). Внутри опции --dns-somednsprovider мы чуть-чуть приврали, так как существует множество способов подтвердить Let«s Encrypt, что вы владеете какой-то определенной порцией интернет-трафика. Но если вы используете какого-то облачного провайдера, такого как DigitalOcean, AWS, Azure, Hetzner, какого угодно — возможно для вас уже существует более простой способ предоставить требуемую для сертификации информацию, потому что ваш провайдер озаботился инструментом интеграции.

После этого, если вы уверены в правильности параметров, передаваемых в CSR с помощью certbot«а к Let«s Encrypt, просто уберите параметр --dry-run из команды и продолжайте.

В случае успеха, клиент вернет вам несколько сертификатов: сам подписанный сертификат, промежуточный и корневой сертификаты, а также сочетание последних в виде цепочки сертификатов, все в .pem формате.

В OpenSSL есть команда которую мы задействуем для того, чтобы посмотреть внутрь сертификата:

openssl x509 -in chainfilepath.pem -noout -text

Сейчас должно уже быть понятно, что Let«s Encrypt подписал сертификат используя алгоритм хеширования SHA256. В дополнение к этому, Let«s Encrypt пока только планирует добавить корневую и промежуточные подписи в ECDSA, поэтому на текущий момент остается довольствоваться промежуточными подписями RSA. Но это не страшно, так как вы в любом случае будете использовать публичный ключ ECDSA.

В конце этого раздела, мы бы хотели добавить немного информации о сравнении длин ключей различных алгоритмов. В информационной безопасности принято говорить, что уровень безопасности составляет 2^x, где x — битовая длина (RSA составляет некоторое исключение, так как растет несколько медленнее экспоненты). Для аппроксимации того, как ключи различных алгоритмов сравниваются между собой, мы сошлемся на страницу вики OpenSSL:

Как вы можете видеть, различия заметны. Хотя пока Let«s Encrypt и позволяет получать подписанные сертификаты только на ключах лишь двух эллиптических кривых — 256 (secp256v