Крестики-нолики, шашки и шахматы: немного об играх в математике
Вы вечно проигрываете в крестики-нолики? Устали от бесконечных издевок окружающих? Чувствуете себя неполноценным членом общества? Тогда вы обратились по адресу! Сегодня у вас есть уникальная возможность пройти наш обучающий курс по беспроигрышной стратегии, который стартует уже сегодня! Присоединяйтесь сейчас и получите скидку 10% по промокоду НЕУДАЧНОЕ_ВСТУПЛЕНИЕ!
❯ 1. Беспроигрышная стратегия в крестики-нолики (или как впасть в состояние «ничейной смерти»)
Так, ладно, скорее всего все и так знают, что в крестиках-ноликах практически невозможно не победить, да и они давно вышли из моды. Но для поддержания уровня занудства, мы все-таки пробежимся по общей стратегии, а затем очень издалека начнем разговор про игры, так что заваривайте чаёк и присаживайтесь. Кто в теме, следующую часть можно пропустить.
Итак, как не проигрывать, если вы ходите первыми (напомню, что в нашем консервативном мире крестики доминируют).
- 1 ход: всегда в центр;
- 2 ход: в угол, который дальше всего от предыдущего хода ноликов;
- 3 ход: защита от попыток нолика чет выстроить или, что вероятнее, — снова ход в угол;
- 4 ход: тут у вас в наличии либо уже имеются две выигрышные линии, и вы гасите его, либо нолик прикрыл тылы, и исход — ничья.
Если вы играете за нолики, то при «идеальном» сопернике (который ходит всегда верно) у вас есть лишь возможность обороняться и выйти вничью, например:
- 1 ход: в любой угол;
- 2 ход:, а дальше только пытаться помешать крестикам замутить тройничок, ведь больше вы ни на что не способны в силу своей submissive сущности.
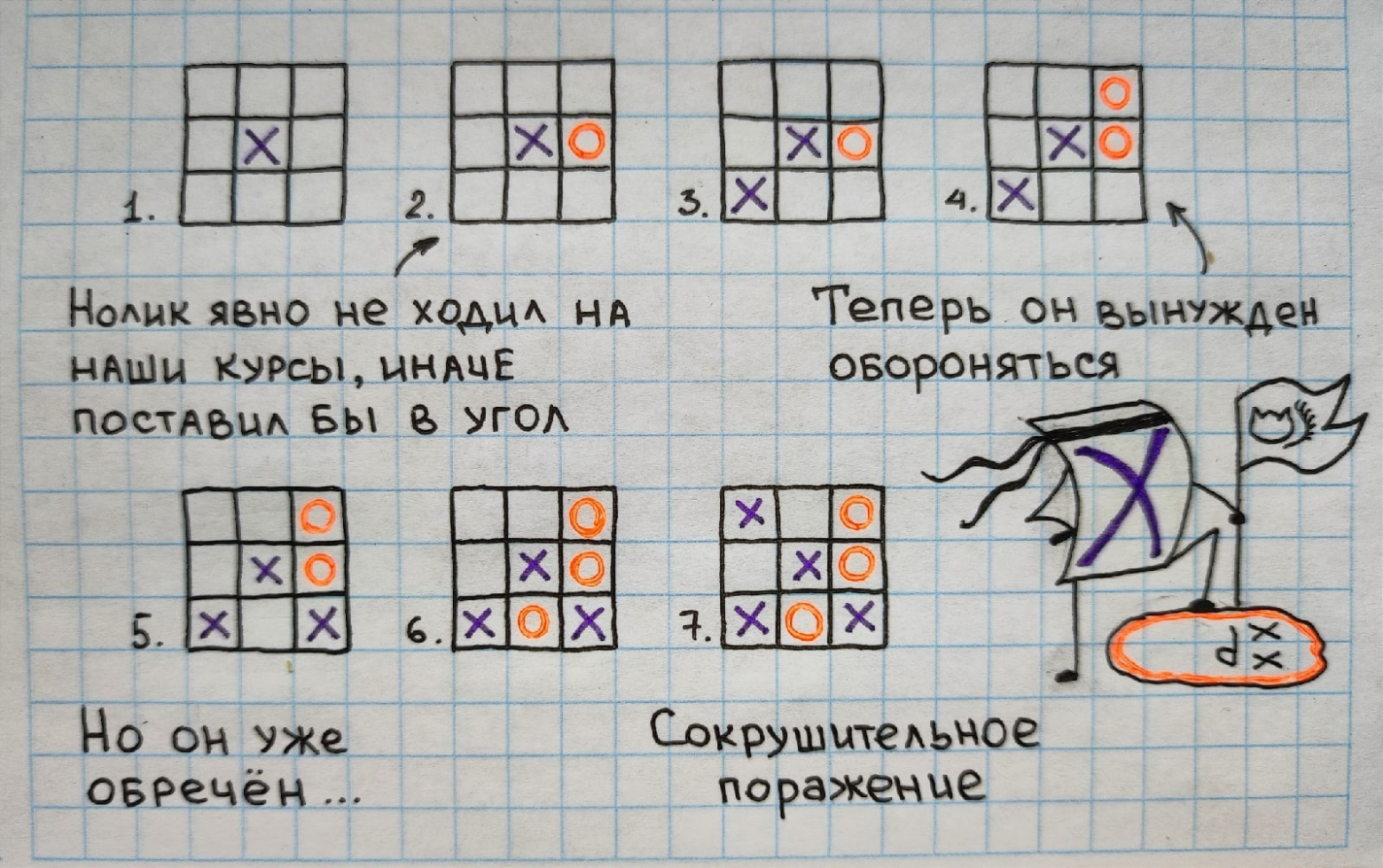
Автор потерял нужную картинку из инета, не судите строго
Как видно, максимальная выгода от этих знаний — спорить с детишками на конфетки (хотя и они быстро раскусят фокус), а программу, способную никогда не проигрывать в крестики-нолики, может написать даже школьник. Самым примитивным методом в данном случае является дерево игровых ситуаций: перебор всех возможных исходов игры, где в конце партии заполнены все клетки поля.
Смотрите, корень нашего дерева — пустое поле 3×3. Первый игрок имеет возможность сделать ход на одну из девяти позиций — рисуем дереву девять веток с разными позициями крестиков (там внизу есть картинка). На следующем ходе у каждой ветки с крестиком есть восемь свободных мест для ноликов, то есть каждой ветке рисуем по восемь новых, где в различных комбинациях на поле две клетки заняты крестиком и ноликом. Итого имеем 9×8 — 72 ветки. Следуя такой логике, на дальнейшем шаге у дерева появится по 7 ответвлений, так как свободно только 7 клеток для крестика, количество теперь веток стало 9×8х7=504. Конечное число решений — листиков нашего дерева — равно 9! (все же знают, что это не девять с восклицанием, а факториал? — 9×8х7×6х5×4х3×2х1) или 362880. Теперь достаточно вбить компьютеру все эти исходы и запрограммировать выбирать только выигрышные.

Первые ветви дерева решений
Но тут даже с первого взгляда понятно, что такой способ слишком «деревянный»: некоторые ветви приводят к победе еще до того, как заполнится все поле, так что мы, по сути, выполняем тонну ненужных вычислений. Нужно уметь не только выбрать кратчайший путь к выигрышу, но и отсечь ненужные ветви — короче, подстричь наше дерево. Первая задача реализуется с помощью алгоритма минимакс, который сводит к минимуму счет противника, максимизируя при этом свой (то есть — выбирая наиболее возможную короткую ветвь). Вторая задача решается методом альфа-бета отсечения, который при переборке различных узлов дерева отсекает заранее проигрышные.
Ну вот, дерево подстригли, причесали — теперь полное количество его узлов сократилось до 256158, и программа всегда будет выигрывать или заканчивать партию вничью за секунды.
Таким образом, крестики-нолики являются примером игры, находящейся в состоянии «ничейной смерти»: любой игрок (даже если он полный чайник, а противник чемпион мира), применяющий правильную теорию, может выиграть или в худшем случае свести ее к ничьей. Такая полностью просчитанная игра теряет смысл, ведь опыт и квалификация игроков больше не имеют веса, и соревновательный момент уступает место вычислениям.
Но крестики-нолики — игра очень примитивная, самая длинная партия в ней равна всего девяти ходам, так что построить и просчитать дерево решений для нее можно даже вручную (развлечение для людей с кучей свободного времени).
Вот, например, с шашками дела обстоят интереснее: кроме большого поля у них и правила на порядок сложнее, так что при подсчетах оказывается, что листьев у дерева решений около 5×10^20. Это пять и рядом двадцать нулей. Думаете, это мало? Оно и понятно, у нас мозг просто не способен представить число такого порядка, но для сравнения: чтобы выстроить цепочку от Земли до Марса из бусинок размером с атом потребуется как раз 5,5×10^20 бусинок. Очевидно, что число это офигеть какое большое, и пятидесяти компьютерам не просто так потребовалось почти 20 лет (двадцать лет, Карл!), чтобы полностью рассчитать все возможные исходы шашек и выстроить их дерево решений.
Сие знаменательное событие произошло в 2007 году благодаря команде канадских исследователей во главе с Джонатаном Шеффером, и с этого момента шашки официально вошли в список полностью решенных игр. Если оба соперника не совершают ошибок, то партия всегда заканчивается ничьей. Тут нужно учесть, что речь идет об английских шашках — чекерс; в них назад бьет только дамка.

Статья Шеффера и его коллег в журнале Science
Таким образом, человек даже теоретически больше никогда не обыграет компьютер в шашки, так как с первого его хода известны все выигрышные решения, и каждый шаг лишь приближает компьютер к победе. Ничейная смерть шашек была предсказана еще в 50-е, и спустя полвека прогноз подтвердился. Но не стоит грустить: если крестики-нолики имеют короткую беспроигрышную стратегию, то для шашек она гораздо-гораздо сложнее, так что и воспользоваться ей может только компьютер. По сути, 2007 был значим только для математиков. Как многие заметили, после 2007 года шашки не умерли, и в игре между двумя человеческими существами решающее значение все еще имеет опыт, а не вычислительные мощности мозга.
Сейчас на меня наверняка налетят шахматные снобы, утверждающие, что приличные люди вообще не играют в шашки. И действительно, а как обстоят дела у шахмат?
❯ 2. Компьютеры, которые играют в игры
Кто победит, если две одинаковые программы устроят между собой шахматный турнир? Будут ли партии всегда заканчиваться вничью или у белых будет преимущество первого хода? И есть ли какая-то выигрышная стратегия, которая позволила бы полному чайнику одолеть чемпиона?
От математики в этой части не осталось ничего, кроме парочки больших чисел, и она является скорее кратким историческим обзором. Однако теория игр без шахмат — как самолет без двигателя, надо чуть-чуть пробежаться по основным моментам.
Итак, по сравнению с великими и ужасными шахматами, шашки (а тем более, крестики-нолики) покажутся развлечением для малышей. Напомню, что для английских шашек количество различных вариантов партий равняется 5×10^20, и полностью просчитать их смогли только спустя 18 лет после начала работы программы.
Тут нужно отдельно отметить, что обыграть в шашки особь вида Homo sapiens компьютер смог гораздо раньше, целью проекта было не научить машину побеждать людей, а знать последствия каждого его хода вплоть до окончания игры.
Напрашивается очевидный вопрос: раз шашки рассчитали, то и шахматы сможем, разве нет? Ждали же 18 лет, подождем и еще. Всё равно простым смертным нет дела до этих математических извращений, и в каком-нибудь 2040 году, листая ленту девятым кибер-пальцем, мы смахнем новость про найденное решение для шахмат.
К сожалению, пока что это утопия. И дело не в том, что математики поняли, что страдают какой-то фигней, проблема заключается в сложности самой игры: одних только позиций фигур на доске существует около 10^46, а уникальных партий — не меньше 10^120.
Десять в сто двадцатой степени. Это много. Так много, что у нас даже нет аналогии, чтобы показать весь ужас этого гигантского числа, его попросту не существует в физическом мире. Чтобы вы понимали, количество атомов в известной нам части Вселенной примерно равно 10^80, а количество оригинальных партий в шахматах больше этой цифры в 10^40 раз. Причем в начале игры все выглядит довольно безобидно: у белых есть всего двадцать ходов — 16 пешками и четыре конями —, но с каждым сделанным шагом количество возможных комбинаций на доске очень быстро растет. Так, например, после первого хода каждого из соперников, на поле существует 400 различных позиций для следующего шага, после второго — 72084, после третьего — больше 9 миллионов, после четвертого — более 288 миллиардов. Такое число соразмерно с количеством звезд в нашей галактике, а ведь это всего лишь самое начало партии.
Однако не просто так было сказано, что теория игр без шахмат — как самолёт без двигателя. После окончания Второй мировой еще на заре эпохи машинных вычислений шахматы стали своеобразным эталоном для проверки различных идей в этой области. Клод Шеннон *кстати, именно в честь него число 10^120 называется числом Шеннона*, один из основателей раздела об искусственном интеллекте, говорил, что не видит практической ценности в вычислении всех возможных шахматных партий, но сама эта мысль побуждает исследователей двигаться вперед и развивать технологии до тех пор, пока они не найдут решение.
Первую программу для игры в шахматы написал еще в 1952 году Дитрих Принц (коллега Алана Тьюринга) на компьютере Ferranti Mark. Правда, тут не стоит обольщаться, этот компьютер, лишь отдалённо напоминающий наши современные устройства, был таким слабеньким, что объем его оперативной памяти мог содержать программу только по типу «мат в два хода». Она была рассчитана лишь для последних двух ходов, но начало шахматной эпопеи было положено.
В 1956 году компьютер MANIAC-1 *милое название* сыграл три партии в облегченные шахматы (на поле 6×6 и без слонов) — сам с собой, против сильного игрока и против новичка. Несмотря на то, что опытный шахматист в начале игры решил отказаться от ферзя, программа все равно ему проиграла *какой неумелый маньяк*, но вот последнего — слабого соперника компьютер смог победить. Это была первая победа машины над человеком.

Название MANIAC, кстати, — это аббревиатура: Mathematical Analyzer Numerical Integrator and Automatic Computer.»… Компания Metropolis выбрала имя MANIAC в надежде остановить поток глупых аббревиатур для названий машин»
После изобретения в 1971 году первого микропроцессора, у ученых появилась возможность задействовать более мощные компьютеры, а значит, сохранять в памяти машины еще больше победных комбинаций. В 1974 году был организован первый чемпионат по шахматам среди программ, в 1978 году машина обыграла международного мастера по шахматам, а в 1981-м Cray Blitz стал первым компьютером, получившим рейтинг мастера.
Но несмотря на то, что с появления первого компьютера, играющего в шахматы, прошло уже много времени, алгоритм программы оставался на уровне решения крестиков-ноликов: легендарный суперкомпьютер Deep Blue от компании IBM использовал типовой метод поиска по шахматному дереву— минимаксный алгоритм с альфа-бета-отсечениями. Преимущество того или иного компьютера заключалось лишь в мощности процессора и количестве загруженных в него победных ходов живых шахматистов.
Кстати, легендарным Deep Blue стал 11 мая 1997 года, когда выиграл матч из шести партий у чемпиона мира Гарри Каспарова. Интересно, что за восемь лет до этого в Нью-Йорке Каспаров победил более слабого предшественника Deep Blue под названием Deep Thought. Тогда он высказал такую мысль: «Если компьютер сможет превзойти в шахматах лучшего из лучших, это будет означать, что ЭВМ в состоянии сочинять самую лучшую музыку, писать самые лучшие книги. Не могу в это поверить. Если будет создан компьютер с рейтингом 2800, то есть равным моему, я сам сочту своим долгом вызвать его на матч, чтобы защитить человеческую расу». Что ж, ему явно пришлось пересмотреть свои взгляды.

Матч 1997 года, который стал предметом документального фильма «Человек против машины»
Окончательно и бесповоротно человечество проиграло железякам в 2005-м: в этот год представитель нашей расы в последний раз смог одержать верх над программой. Сегодня рейтинг живых шахматистов настолько отстал от их железных соперников, что человеку больше никогда не выиграть партию с машиной. На начало сентября 2022 года наивысший шахматный рейтинг человека составляет 2861, а программы 3535.
Чувствуете, как повеяло киберпанком? Но несмотря на такие потрясающие успехи компьютеров, сама игра так и остается нерешенной: нам неизвестно, как закончилась бы идеально просчитанная партия, где обе программы знают последствия каждого хода вплоть до конца игры. Ученые лишь предполагают (но до сих пор не могут доказать), что белые обладают преимуществом первого хода, так как в идеальной игре черные могут только реагировать на создаваемые ими угрозы. Некоторую надежду в этой области вселяет активное развитие квантовых компьютеров, которые могут вести поиск одновременно по нескольким ветвям дерева решений, но тем не менее какого-то революционного алгоритма для самого поиска мы не имеем, и идеальной стратегии для чайников не существует.

Рейтинг живых шахматистов с официального сайта FIDE на начало сентября

Рейтинг шахматных программ
Хотя еще в 1960-х шахматы были своеобразным испытательным полигоном при проверке различных методов создания искусственного интеллекта, сложные стратегические игры и сегодня служат этой цели. В чистом виде они не представляют особой ценности, но подходы, используемые для обучения и самообучения машин, имеют большое значение для науки. Кроме того, мне кажется, сама мысль о том, что мы знаем, как рассчитать шахматы, но пока просто не имеем для этого ресурсов, очень вдохновляет.
❯ 3. Go play Go (Последний бой людей)
Оказалось — человек так отстал от своих железных собратьев, что больше никогда не сможет одержать над ними верх. Но что, если бы существовала игра, где люди могли бы проявлять свои сильные стороны, не присущие машинам? Где победа зависит не только от строгих логических расчетов, но и от силы воображения и хитрости?
Как вы уже поняли, такая игра есть: мы наконец-то добрались до го. Го — китайская стратегия — является самой древней настольной игрой, сохраняющей свои правила практически неизменными вот уже 2500 лет. До ХХ века игра была распространена только в Азии, но на сегодняшний день она входит в пять дисциплин Всемирных интеллектуальных игр и является самой распространенной настолкой по числу участников (c поправочкой на плотность населения Востока).
В Китае го образно называют «разговором рук» *italian_moment*, что подчеркивает особое отношение к игре как к искусству. Это неудивительно, ведь ее правила невероятно сложны, так что напоминают не соревнование, а своеобразный диалог, и у разных мастеров есть даже свои собственные стили, по которым их узнают — как стиль писателя или манера художника.
Чтобы сыграть в классическую версию го вам понадобятся: доска в клетку 19×19 (называется гобан) — 1 шт, белые игральные камни — 180 шт., черные игральные камни — 181 шт., кошка-жена — 1 шт. (если есть больше, поделитесь?). Цель игры — отгородить на доске камнями своего цвета бо́льшую территорию, чем противник. Как видно, здесь нет черных и белых клеток на поле, камни можно ставить на любые пересечения линий, нет и разграничения игральных фигур — все они равноценны друг другу. Собственно, именно эта простота и порождает дьявольски сложные тактику и стратегию.

Напомню, тактика — локальное противоборство в какой-то части поля. Стратегия — общее положение сил в игре. Если в шахматах вы лишились дорогой фигуры, ваши шансы на победу обычно заметно уменьшаются, то есть тактика очень сильно влияет на стратегию. В го и поле больше, и фишек огромное количество — поэтому хитрости и поддавки здесь вполне могут стать более близким путем к победе, чем прямая и открытая политика завоевания.
Обычный метод перебора, которым пользуются компьютеры для выбора выигрышной стратегии в шахматах, здесь просто не уместен. Во-первых, дерево решений го необычайно огромно — на начальной позиции существует 55 вариантов ходов (в шахматах — 20), и «растет» оно быстрее — после первых двух ходов соперников существует уже около 16 миллиардов позиций для следующего (в шахматах — меньше ста тысяч). А во-вторых, го — игра, в которой очень важен опыт.
Настоящий мастер способен оценивать ситуацию на поле с помощью распознавания визуальных образов, а человеческий мозг приспособлен к этому гораздо лучше компьютера. Умение узнать на доске некий общий рисунок, который не повторяется каждый раз в точности — задача для машины куда более сложная, чем просто молниеносный подсчет. Именно по этой причине даже после первых серьезных проигрышей людей в шахматы, считалось, что компьютерам не скоро удастся добиться того же в го.
Но вот настал 2016 год и программа AlphaGo, разработанная корпорацией Google, в прямом эфире победила мирового мастера с девятым даном — Ли Седоля. Это стало возможно благодаря новому подходу обучения, который кардинально отличается от обучения шахматных компьютеров. Помните, что Deep Blue использовал обычный метод перебора дерева решений просто с кучей оптимизаций и на самом деле кроме мощных процессоров и больших объемов памяти он недалеко ушел от железяк 60-х.

AlphaGo — революционная программа, в ней нет базы данных с удачными ходами чемпионов или оценочного алгоритма, лишь самые базовые правила, которым учат новичков. Всему остальному она научилась сама, проигрывая тысячи партий с собой. В основе компьютера лежит нейронная сеть, моделирующая работу органического мозга. Главное новшество AlphaGo заключается в использовании глубинного обучения — метода, успешно применявшегося для распознавания образов (например, для поиска картинок в Google Images). Но как ни парадоксально именно из-за этого разработчики не знают, каким конкретным образом программа оценивает ситуацию в игре: система настолько сложна, что анализировать все уровни обработки информации в целом не представляется возможным.
Синтез интеллектуального подхода, свойственного людям, и высокой скорости вычислений делает AlphaGo уникальной. Методы, реализованные в этом проекте, сейчас проходят проверку для применения подобных программ жизни. Уже сегодня они помогают выстраивать модели химических реакций в живых организмах и могут диагностировать некоторые заболевания на ранних стадиях.
Довольно простая статья о работе AlphaGo.
Поэтому как ни грустно признавать наше поражение по всем фронтам (и в шашках, и в шахматах, и даже в го) — все же мы не проигрываем впустую. Такие программы, как AlphaGo только лишний раз доказывают невероятную силу человеческого разума и задают высокую планку для следующих поколений. Несмотря на окончательную победу машин, го не только не потеряла статус интересной настольной игры, но и вышла за эти рамки, став важным этапом в истории развития искусственного интеллекта, также как шашки или шахматы.

