Коварные перцентильные фильтры
В жизни каждого A/B-эксперимента наступает момент, когда пора проанализировать его результаты и понять, а не зря ли мы пилили все эти фичи.
Всем привет! Меня зовут Костя Житков, я — аналитик в команде Поиска рекомендаций hh.ru. В этой статье я расскажу о том, как мы чуть не увязли в самообмане во время анализа одного из наших A/B-экспериментов.
Нужен отклик
Большинство действий пользователя на сайте можно измерить количественно — мы можем посчитать число просмотров страничек вакансий, количество поисков или откликов. Такие замеры мы называем метриками и пользуемся ими, чтобы убедиться, что новые фичи делают жизнь пользователя лучше. Это мы понимаем через эксперименты, которые выглядят примерно так: одной части пользователей мы показываем новый вариант сайта/приложения, а другой — старый, затем считаем релевантную для эксперимента метрику в каждой из групп, применяем статистический критерий и делаем выводы, как именно изменилась жизнь пользователя с появлением новой фичи.
Одна из метрик, которой мы часто пользуемся в наших A/B-экспериментах — это отклики. Сейчас покажу, как эта метрика выглядит в реальной жизни, и что нужно сделать, чтобы попасть в статистику откликов в эксперименте.
Заходим на сайт, вводим в поисковую строку, например, «data scientist». Перед нами открывается поисковая выдача и мы видим, что у каждой вакансии есть синенькая кнопка «Откликнуться». Если нажать на нее, произойдет отклик, это и будет нашей метрикой.
Отклик на сайте
Попробуем интуитивно понять, как часто пользователи откликаются на сайте. Представим, что вы — пользователь. Вы ввели в поиске «data scientist» и увидели вакансии, которые вам относительно интересны. Затем откликнулись на первую, третью и пятую вакансии — сделали три отклика за день. Завтра вы вновь стали искать вакансии с тегом «data scientist» и решили откликнуться уже на четвертую в выдаче. Однако для нее приходится написать сопроводительное письмо. Писать письма — долго, но вы справились, а затем отправили отклик. Увы, но боевой запал на этом иссяк, и больше в этот день вы откликов не отправили. На следующий день вы в третий раз изучили результаты поиска и не нашли новых интересных вакансий. Поэтому сегодня вы не откликались и вовсе.
Таким образом за неделю у вас наберётся 5 откликов, а если повезёт — 10. Ваши знакомые могут вести себя похожим образом, и у них тоже накопится примерно столько же. Из таких рассуждений кажется, что в среднем пользователи могли бы откликаться на вакансии 4–5 раз в неделю. Похожа ли эта интуиция на реальное распределение откликов?
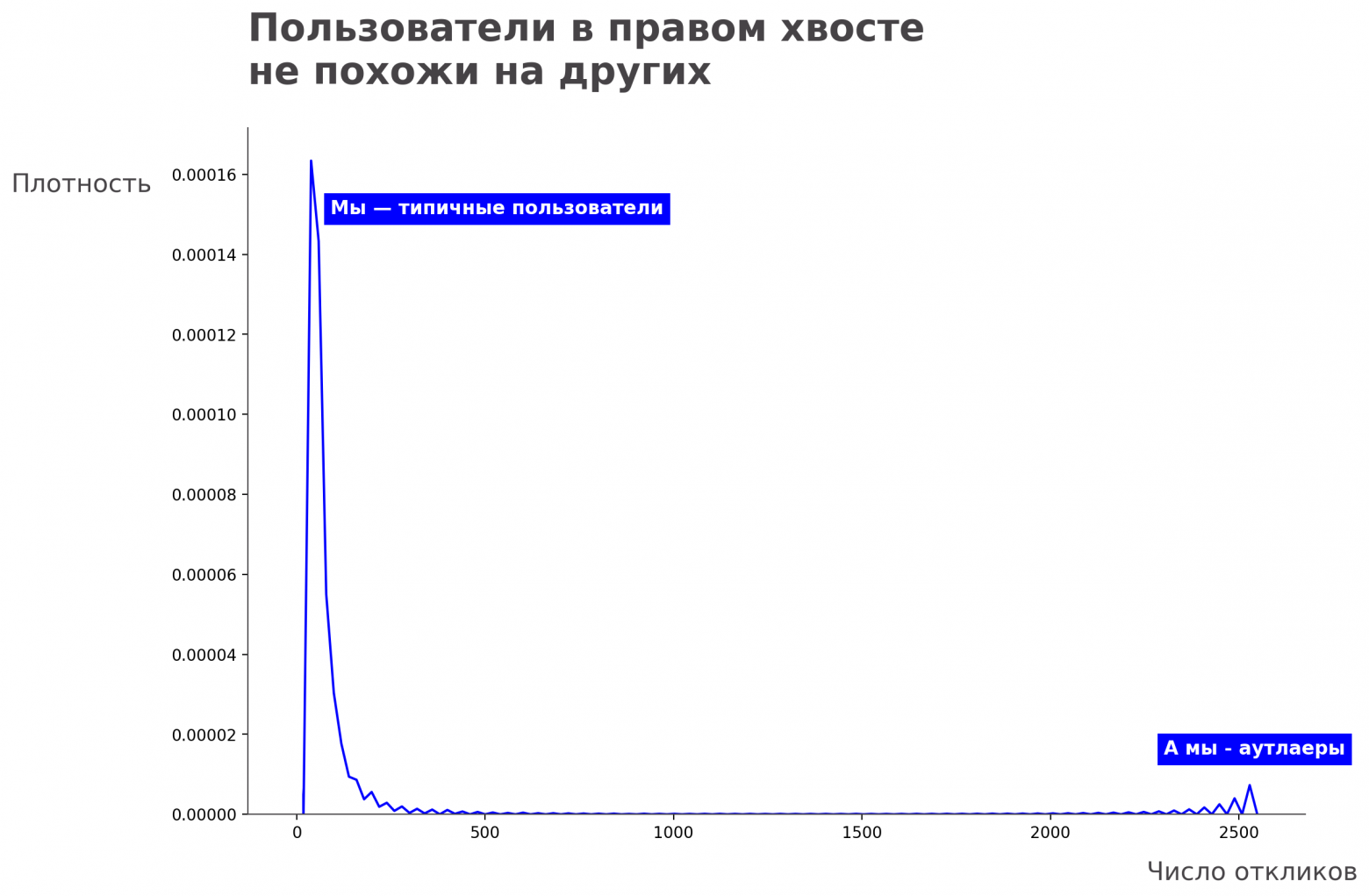Распределение пользователей по числу откликов в течение двух недель
Наша интуиция справедлива только отчасти: есть пик слева, где действительно много пользователей, которые откликаются мало (или не откликаются вовсе), но также мы видим пик справа. Это пользователи, которые откликаются очень много — так называемые выбросы или аутлаеры. Может ли второй пик как-то помешать нам в A/B-экспериментах? К сожалению, да.
Необычный пользователь может сильно перекосить значения метрик в эксперименте. Из-за этого растет их дисперсия, и мы не сможем увидеть значимого изменения в тесте. Как бороться с этим? Самое простое, что можно сделать — просто отфильтровать. Если у вас нет времени на анализ A/B-теста, можно просто сказать: «эти ребята слишком необычные, наши пользователи выглядят по-другому, давайте мы их просто «откинем». Посмотрим, как выглядел бы график без них.
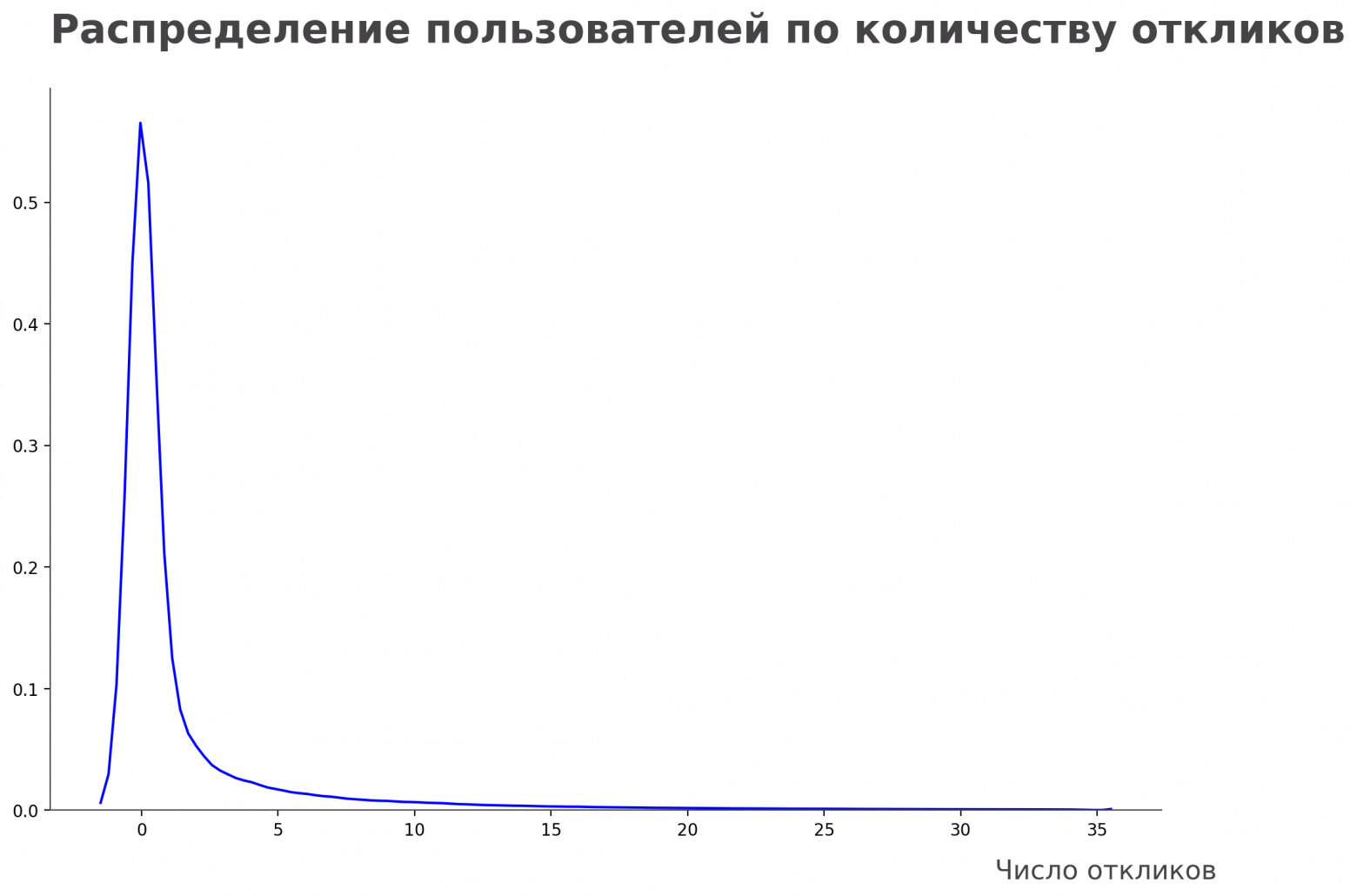Откинули самых откликающихся пользователей на глаз
Справа остался хвост, но он стал значительно меньше — число 35 выглядит куда привлекательнее, чем 2500. Кажется, мы решили проблему.
Но сколько вообще пользователей нужно «откидывать», и как определить, что пользователь действительно необычен? Увы, на этот вопрос нет однозначного ответа. На графике выше я сделал это на глаз. Просто выбрал некоторое число и убрал всех пользователей, которые откликались больше него. Можно сделать процедуру более формальной: давайте теперь откидывать некий процент самых откликающихся пользователей — введём перцентильную границу отсечения. Например можно откинуть 1% пользователей, которые откликались больше всего. В такой процедуре всё равно остается неопределенность, какой процент выбрать. Выкидывать один или три — мы не знаем, универсального ответа не существует, но можно итеративно прийти к подходящему варианту. Покажу, как мы это сделали на примере одного из наших экспериментов.
Результаты эксперимента
Посмотрим на то, как влияет перцентиль на результаты статистического теста на примере одного из наших экспериментов.
Каждая точка на графике — это отдельный статистический тест, а красная линия — уровень значимости (или вероятность false positive). Если синяя точка опускается ниже красной (p-value* < уровня значимости, равного 5%), значит тест статистически значим, и мы можем уверенно принимать решения о раскатке изменений на всех пользователей.
* Что такое P-value?
P-value — вероятность наблюдать текущее или более экстремальное значение тестовой статистики при условии, что верна нулевая гипотеза. Проще говоря, насколько удивительными нам кажутся наблюдаемые данные при условии, что верна нулевая гипотеза.
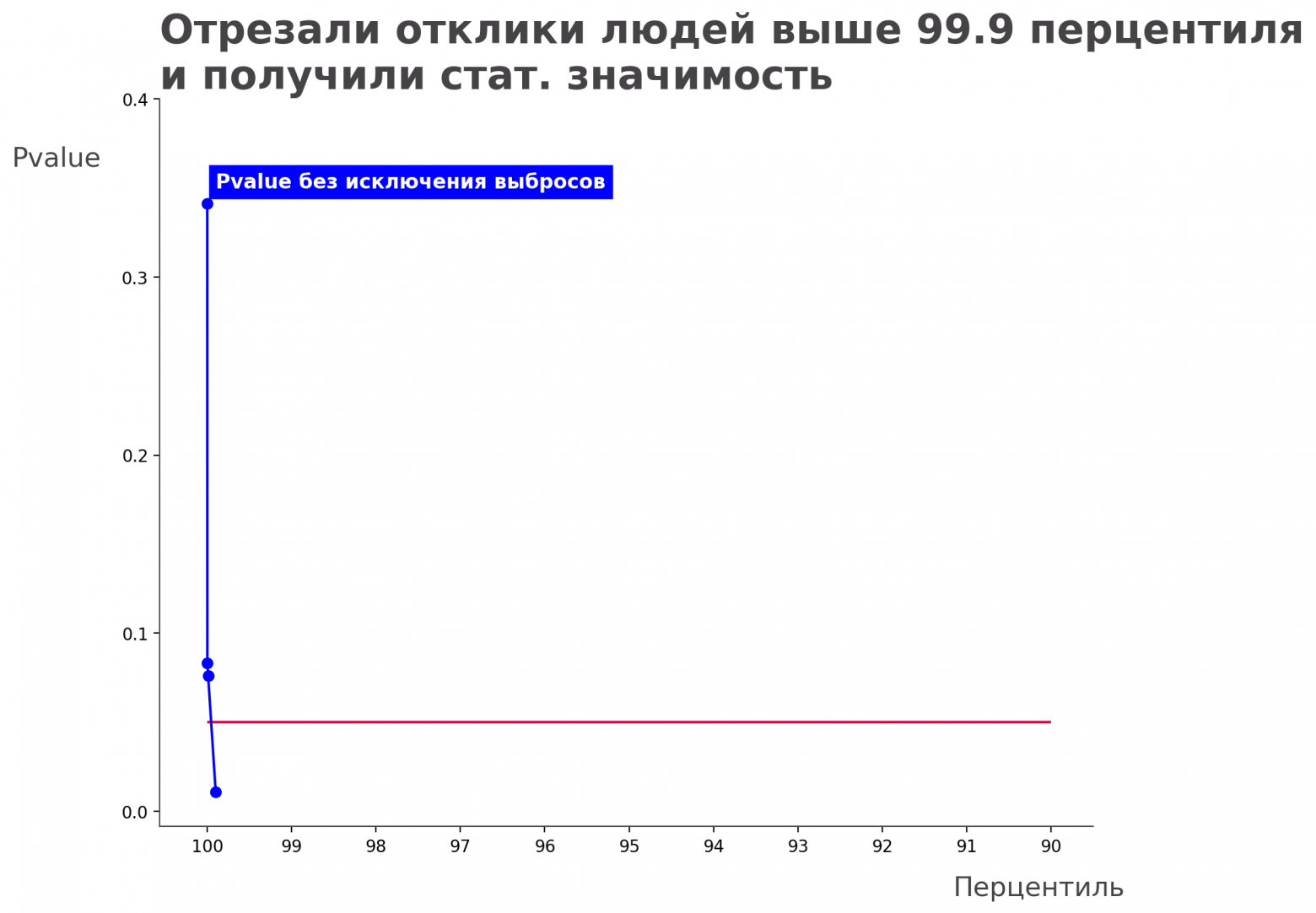
Когда мы посчитали результаты без перцентильного фильтра, то увидели что P-value выше красной линии, и результаты не были статистически значимы. Соответственно мы не знали: эффект слишком маленький и мы его не поймали или его вовсе нет. В этом эксперименте мы тестировали модель машинного обучения, которая показала хорошие приросты в офлайн замерах, поэтому не верили, что эффекта нет и стали анализировать эксперимент более подробно.
В ходе анализа мы обнаружили, что есть необычные пользователи с очень высокими значениями метрики и решили откинуть их с помощью перцентильного фильтра 99,99. Так мы откинули самую малость пользователей — 0.01, которые откликались совсем много. Тут же изменения стали статистически значимы, тест прокрасился в зеленый и мы решили выкатывать новшества. Казалось бы, хэппи энд. Но не тут-то было.
Не слишком честно
Итак, мы провели эксперимент, взяли перцентиль 99,99, получили статистически значимое изменение — всё здорово, покатили. Однако мы могли взять перцентиль 98, 97, 96 — практически любое число, и у нас нет никакой гарантии, что в этом случае мы увидели бы статистически значимое изменение. Вот так выглядел бы этот график, если бы мы продолжили перебирать перцентили.
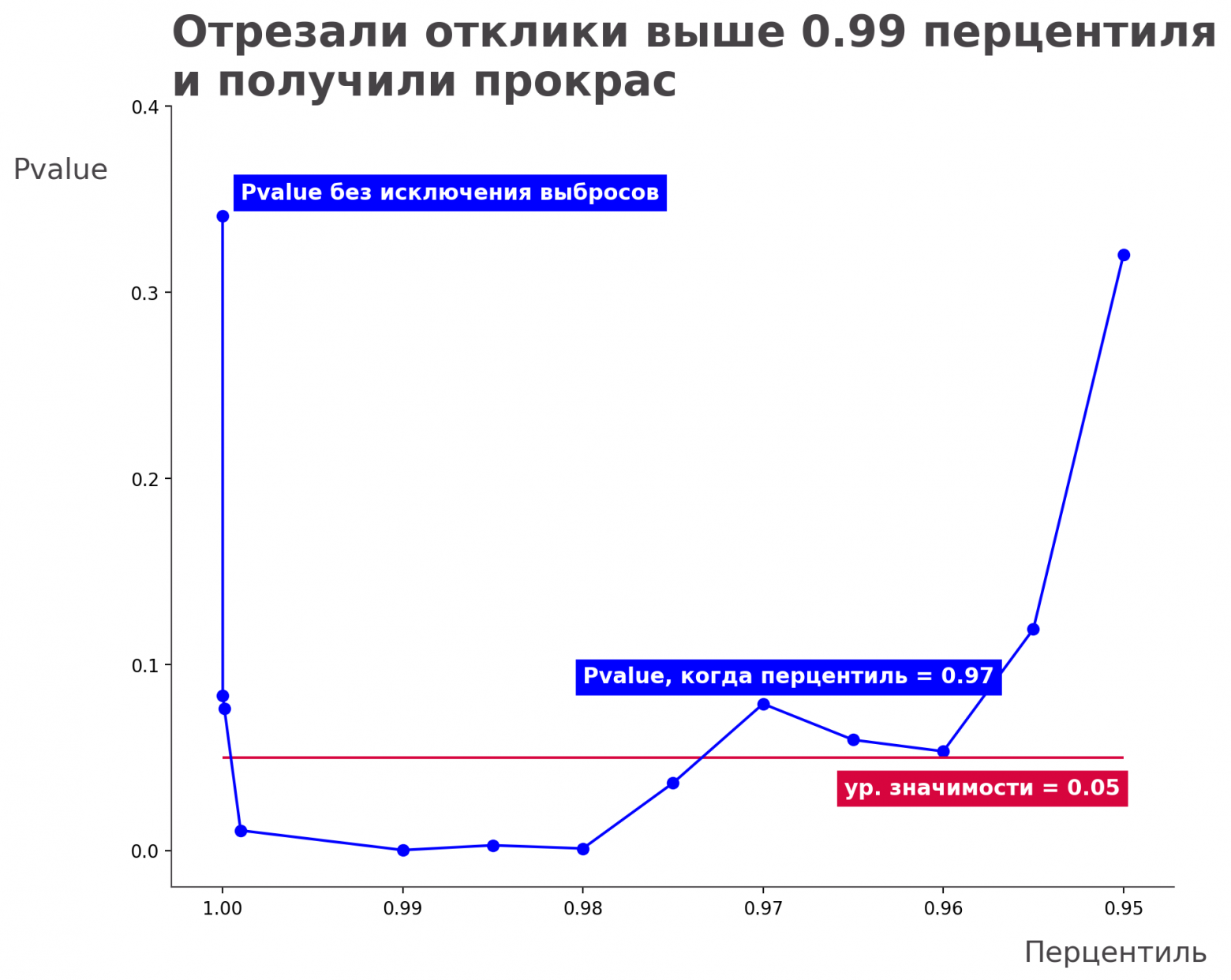прокрас = стат. значимость
Если бы мы выбирали перцентили вплоть до 97 и «откидывали» не больше трех процентов пользователей, мы бы всё ещё получали статистическую значимость. Но при этом, если бы мы стали бы откидывать четыре процента пользователей и больше, то вновь попали бы в серую зону. А значит, у нас не было бы никаких статистически значимых изменений, зато к нам вернулась бы неопределенность в эксперименте.
Выходит, что нам просто повезло с выбором. И с помощью подбора перцентиля мы сможем получить статистически значимые изменения. Другими словами у нас всегда есть возможность что-нибудь где-нибудь подкрутить и увидеть результат, который нам больше нравится. Выглядит не очень честно.
А может дело конкретно в этом эксперименте? Попробуем построить аналогичный график для других и посмотреть, как ведет себя P-value в зависимости от применяемого нами перцентильного фильтра.
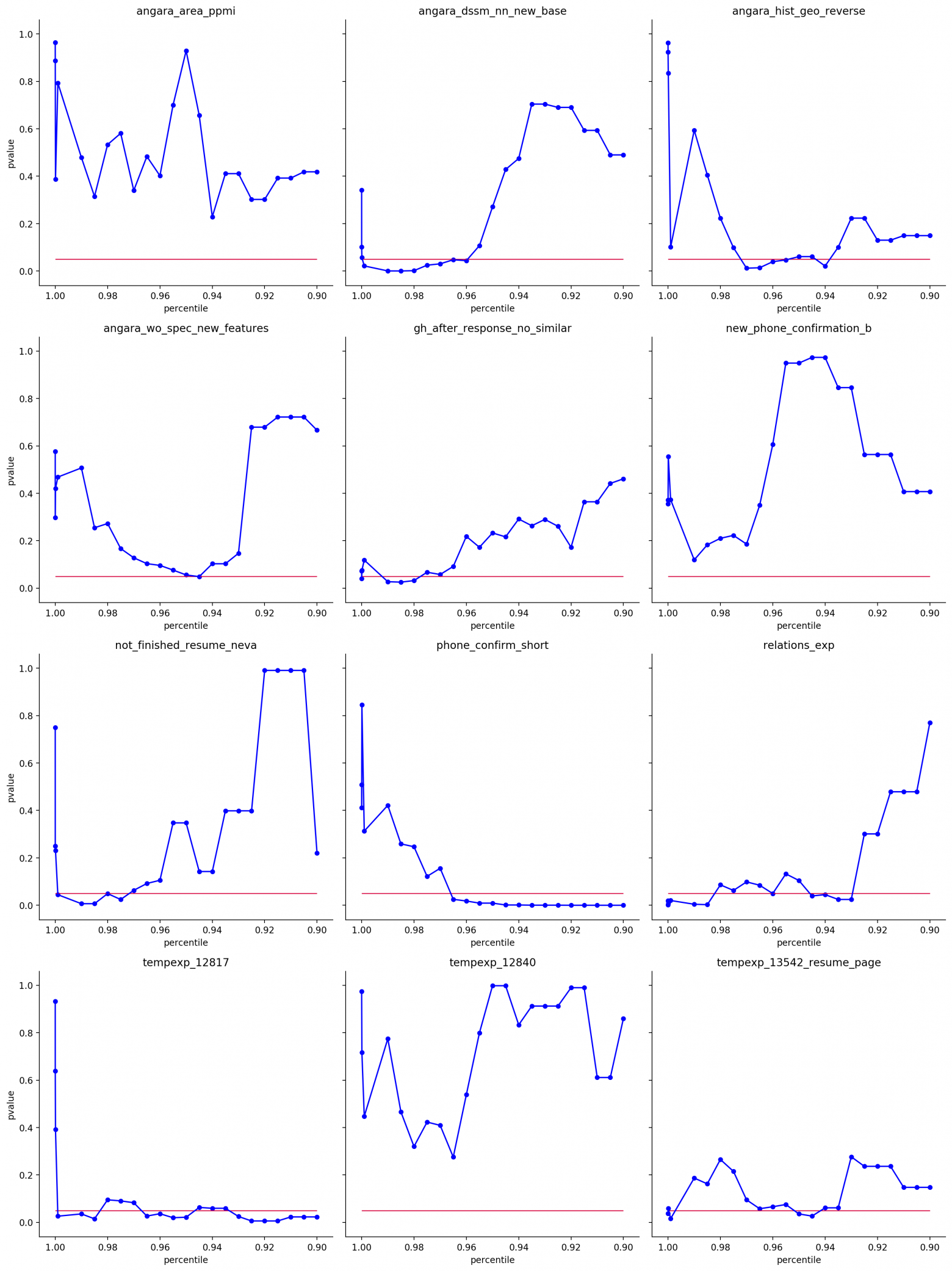Каждый график — это отдельный эксперимент
Заметно, что хаотичность сохраняется, не видно явного паттерна, мы то заходим в зону статистической значимости, то выходим. Нет ничего, что явно указывало бы на тот перцентильный фильтр, с которым будет всегда классно всегда.
Обобщим результаты для всех наших экспериментов за 2021 год. Посмотрим, сколько бы прокрасов мы получили, если бы разрешили перцентилю меняться в определенных границах:
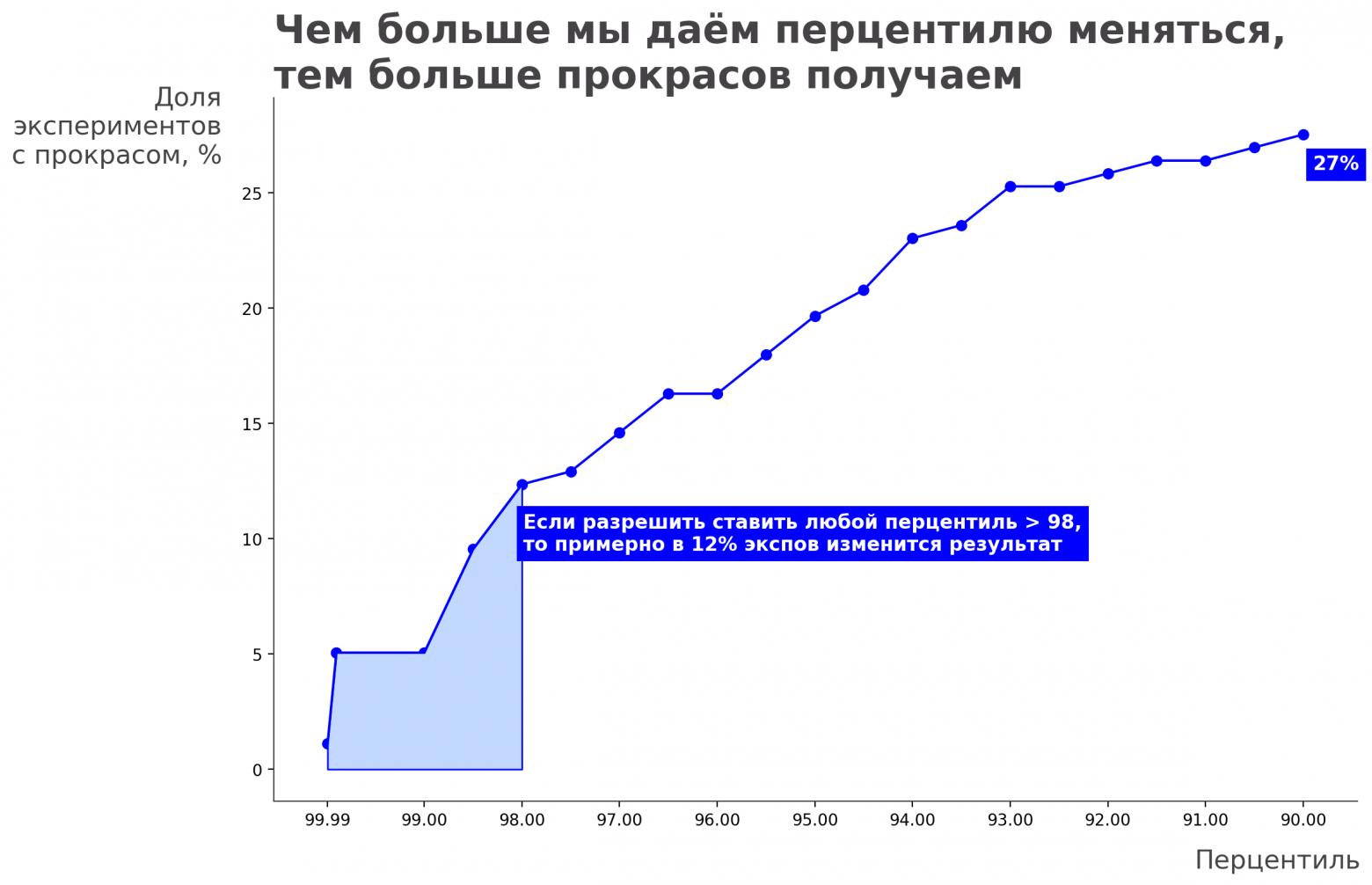
Как читать график: возьмем все наши эксперименты и в каждом будем ставить перцентиль после завершения эксперимента, но зададим некоторые границы. Например, в каждом эксперименте будем ставить перцентиль только от 98 до 99 или от 98 до 95. Мы можем менять разное окно и говорить что давайте в каждом эксперименте любой перцентиль, но только в этом окне. А потом в зависимости от окна можно посмотреть сколько дополнительных прокрасов мы получили (т.е. в скольких экспериментах до манипуляций не было статистической значимости).
Вот как будет меняться число экспериментов, которые изменят свой результат, в зависимости от установленных границ:
Если мы разрешим перцентилю меняться от 98 до 99,99, то в двенадцати серых экспериментах мы сможем получить прокрас — статистически значимый результат
Если бы мы установим окно от 90 до 99,99, то получим прокрас уже в 27% экспериментов, в которых его не было раньше.
В поисках проблемы
Причин, по которым всё это происходит, несколько. Чтобы понять, в чем дело, давайте ещё раз внимательно посмотрим на процесс принятия решения:
Шаг 1. Посчитали эксперимент.
Шаг 2. Взяли разные перцентильные фильтры.
Шаг 3. Пересчитали эксперимент с разными фильтрами.
Т.е. каждый раз мы считали тест с разными входными данными, поэтому и получили разные результаты — звучит логично. С точки зрения математики здесь всё чисто. Проблемы кроются исключительно в нашем процессе экспериментирования.
Первая причина проблемы заключается в том, когда мы подбираем перцентильный фильтр, то, по сути, создаем разные метрики. Мы создали метрику, которая соответствует фильтрам 95 и 90, и уже после эксперимента добавляем их и считаем результаты — если хоть одна из них прокрасилась, мы ликуем. Это очень похоже на проблему множественного тестирования, только там мы добавляем много метрик, которые характеризуют разные стороны продукта. Только здесь — одна метрика, но с разным перцентилем. Результат всё равно аналогичен — из-за большого числа метрик, вероятность false positive станет уже не 5%.
Вторая причина кроется в том, как выглядит сам эксперимент. Например, он серьезно изменяет интерфейс: мы заводим прыгающую кнопку или бегущую строку, а люди начинают активнее откликаться. Именно из-за специфики конкретно этого эксперимента некоторые пользователи станут аутлаерами. Соответственно, процесс подбора пользователей в эксперимент будет связан с нашим перцентильным фильтром, который мы устанавливаем уже по завершении. Выходит, мы снова подкручиваем тот результат, который хотим.
Получается, что проблема не в перцентильном фильтре, а в самом процессе принятия решений по эксперименту. Когда мы крутим перцентильный фильтр после, нам сложно удержаться и не сделать выбор в пользу того значения фильтра, которое соответствует нашим ожиданиям от эксперимента.
Решение
Чтобы избежать такого соблазна, стоит зафиксировать перцентильный фильтр до эксперимента. Однако это не решает проблему эксперимента, который заставляет пользователей совершать определенные действия в большом количестве, например, много откликаться из-за очередной очень яркой кнопки.
Чтобы разобраться с этим, стоит отфильтровать выбросы на предэкспериментальном периоде. Например, если эксперимент начинается первого ноября, следует отфильтровать пользователей, которые вели себя необычно в сентябре. Тогда получится, что эти пользователи необычны сами по себе, и это их свойство никак не связано с нашим экспериментом.
Также важно отметить, что если у вас по каким-то причинам не получается фильтровать пользователей в предэкспериментальном периоде, то любой другой выбранный вами способ фильтрации аутлаеров стоит проверить на соответствие ожидаемому числу ошибок первого рода (false positive). Для этого можно провести множественные АА симуляции для каждого из вариантов применения фильтрации пользователей (до эксперимента, во время эксперимента или ещё как-то) и сравнить реальный уровень ошибок первого рода с ожидаемым. Если этого не сделать, то можно оказаться в ситуации, когда метрика ошибочно красится в 10% случаев, хотя мы думаем, что таких случаев только 5%.
Вместо заключения
На этом у меня всё. Желаю вам договариваться заранее и фиксировать перцентильные фильтры до начала А/В-эксперимента, аккуратно анализировать свои тесты и не подгонять статистику под ваши любимые фичи, даже если они вам очень сильно нравятся.
