Кош на комплексной плоскости
В какой-то из весенних дней этого года я ехал в троллейбусе и листал комикс о Коше. В одном из выпусков была такая фраза «НО! Её можно понять, она же фракталами в горизонт перетекает, я бы тоже замешкался…». После этого я посмотрел в окно и понял, что если мы возьмём два подходящих дробно-линейных преобразования комплексной плоскости a (z) и b (z), и рассмотрим систему итерированных функций для a (z), b (z), a−1(z), b−1(z), взяв в качестве начального множества картинку с Кошем, то Кош будет перетекать фракталами в горизонт! И вот несколько дней назад у меня дошли руки, чтобы написать нужный скрипт на питоне. Результаты мне и моим друзьям понравились, и я решил написать эту хабрастатью.
Итак, если вы хотите узнать, что такое дробно-линейные преобразования комплексной плоскости, и как с помощью них получать фрактальные картинки, то добро пожаловать под хабракат. Там будет немножко бесполезной математики и много гифок.
Итак, возьмём Коша К и поместим его на комплексную плоскость:

Что мы можем с ним сделать? Например, можем сдвинуть в каком-нибудь направлении. Такое преобразование запишется в виде f (z) = z + a, где a — некоторое комплексное число.

Мы можем повернуть Коша на угол φ относительно начала координат. Такое преобразование запишется в виде f (z) = eiφz.

Наконец, можем взять и увеличить Коша в k раз относительно начала координат. Как несложно догадаться, такое преобразование запишется как f (z) = kz.

Любое же линейное комплексное преобразование f (z) = az + b можно представить в виде композиции этих трёх.
Теперь пусть у нас есть некоторое преобразование f (z). Возьмём композицию этого преобразования с самим собой, получим преобразование f (f (z)) = f2(z), потом возьмём композицию f (z) и f2(z) получим преобразование f (f2(z)) = f (f (f (z))) = f3(z) и так далее до бесконечности. Например, если f (z) = z + a, то fn (z) = z + na. Применяя эту серию преобразований к нашему Кошу и объединяя результат, получим что-то такое:
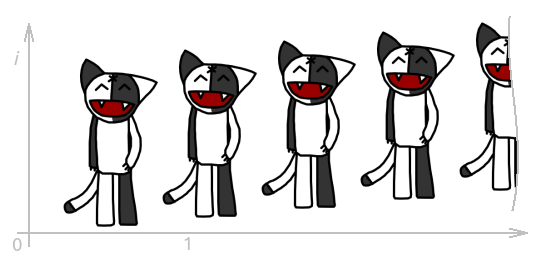
Но, например, если возьмём f (z) = keiφz (сжатие с коэффициентом k плюс поворот на угол φ), то получим уже более интересную картинку: спираль из Кошей. (При построении этой картинки исходный Кош был размещён так, чтобы точка 1 была у него на груди, k = 0,8, φ = π/3.)

Обращу внимание на тот факт, что спираль сворачивается в точку 0.
Наряду с положительными степенями отображения f (z) мы можем рассмотреть нулевую и отрицательные. С нулевой всё просто — это тождественное отображение: f0(z) = id (z) = z. С отрицательными чуть сложнее: нужно сначала обратить преобразование f (z), а затем рассмотреть положительные степени преобразования f−1(z). Для преобразования f (z) из предыдущего абзаца f−1(z) будет растяжением с коэффициентом k и поворотом на угол −φ. Поэтому, если на Коша подействовать всеми целыми степенями преобразования f (z) и объединить результаты, то получим бесконечную в обе стороны спираль из Кошей.
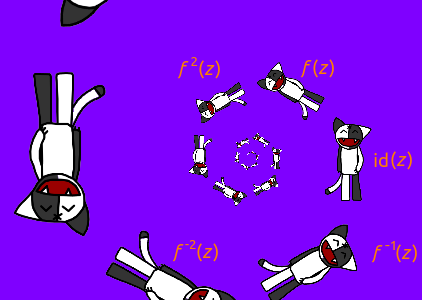
Спираль это конечно хорошо, но давайте немного оживим изображение, для этого заметим, что если на эту спираль подействовать преобразованием f (z), то ничего не изменится. В самом деле, любой из Кошей fn (K) перейдёт в f (fn (K)) = fn+1(K), но такой Кош уже в спирали есть. А в fn (K) перейдёт Кош fn−1(K). Если мы хотим сделать гифку из N кадров, то нужно придумать такое преобразование g (z), что gN (z) = f (z). Но это просто: g (z) = k1/Neiφ/Nz, то есть g (z) сжимает в N раз меньше и поворачивает на угол в N раз меньший, чем f (z).

К спирали мы ещё вернёмся, а теперь немного фракталов. Для удобства введём следующие обозначения ta (z) = z + a — сдвиг на a, rφ (z) — поворот на угол φ и sk (z) — сжатие в k раз. Рассмотрим три преобразования:
f1(z) = ti (rπ/2(s0,6(z))), f2(z) = tsqrt (3)/2 − 0,5i (r (−π/6(s0,6(z))), f3(z) = t−sqrt (3)/2 − 0,5i (r−5π/6(s0,6(z))).
Предположим, что начало координат находится в центре Коша, что делает преобразование f1(z) с Кошем? Оно его сжимает почти в два раза, далее кладёт на правый бок и поднимает вверх на единицу. (Обращаю внимание, что преобразования нужно читать справа налево.) Что-то похожее делают и остальные два преобразования — эти преобразования подобраны так, чтобы уменьшенные копии Коша оказались в вершинах правильного треугольника.
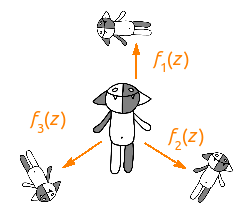
Но мы же не хотим ограничиваться тремя Кошами, их нам нужно бесконечно много, поэтому рассмотрим всевозможные композиции преобразований f1(z), f2(z) и f3(z): id (z), f1(z), f2(z), f3(z), f1(f1(z)), f1(f2(z)), f1(f3(z)), f2(f1(z)), f2(f2(z)), f2(f3(z)), f3(f1(z)), f3(f2(z)), f3(f3(z)), f1(f1(f1(z))), f1(f1(f2(z))), …, f3(f1(f2(f3(f1(z))))), … Подействуем на Коша всем этим множеством преобразований, а результаты объединим. Результат предсказуем и приведён ниже.

Снова добавим анимации, в этот раз сделаем, чтобы копии Коша вращались вокруг большего Коша. Как этого добиться? Предположим что мы хотим сделать N кадров, для кадра k рассмотрим подправленные преобразования f1'(z) = r2πk/(3N)(f1(z)), f2'(z) = r2πk/(3N)(f2(z)), f3'(z) = r2πk/(3N)(f3(z)). Эти преобразования отличаются от исходных тем, что переводят Коша в вершины правильного треугольника, который повёрнут на угол 2πk/(3N) относительно исходного. Результат приведён ниже.

Все преобразования выше были линейными, с помощью них много интересного не сделаешь. Рассмотрим преобразование: f (z) = 1 / z — инверсия плюс отражение относительно действительной оси. Что произойдёт с нашим Кошем, если на него подействовать этим преобразованием? Если начало координат не внутри Коша, то ничего страшного, Коша нужно сначала инвертировать относительно единичной окружности, а затем отразить относительно действительной оси, а если 0 будет внутри Коша, то его просто напросто разорвёт (так как на ноль делить нельзя). Ниже приведено несколько примеров.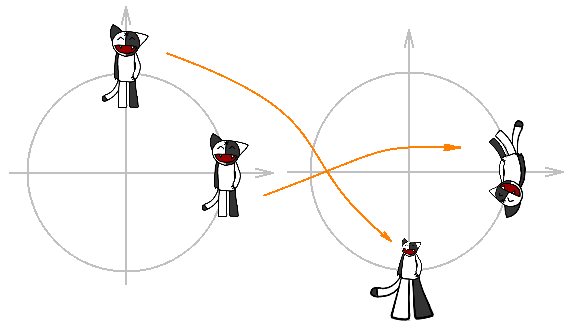
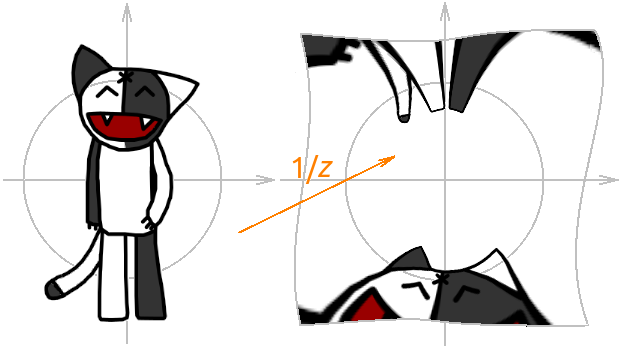
Заметим, что преобразование 1 / z внешность единичной окружности переводит во внутренность единичной окружности, а внутренность единичной окружности во внешность.
Теперь рассмотрим преобразования вида f (z) = (az + b) / (cz + d). Именно такие преобразования называются дробно-линейными. Любое такое преобразование можно представить в виде композиции уже известных нам, а именно: f (z) = f4(f3(f2(f1(z))), где f1(z) = z + d/c — сдвиг, f2(z) = 1 / z — инверсия плюс отражение, f3(z) = −(ad − bc) / c2z — сжатие/растяжение + поворот, f4(z) = z + a/c — ещё один сдвиг. Поэтому если задано какое-то преобразование, то можно быстро понять, что оно делает.
Удобство же рассмотрения преобразования именно в виде дроби в следующем: очень просто находить композиции дробно-линейных преобразований и обращать дробно-линейные преобразования тем, кто умеет работать с матрицами. В самом деле, если, преобразованию поставить в соответствие матрицу 2×2, в которой очевидным образом расставлены коэффициенты a, b, c, d, то композиции соответствует произведение матриц, а обращению — обращение матрицы.
Второе удобство заключается в том, что сразу по записи видно, в какую точку переходит точка 0, а в какую точку — бесконечность, а также какая точка перейдёт в 0, а какая — в бесконечность.
Ещё одним важным для нас свойством является тот факт, что прямые переходят в прямые или окружности, а окружности тоже либо в прямые, либо в окружности. Более точно: если прямая или окружность содержит точку, которая уйдёт в бесконечность, то она станет прямой, иначе же станет окружностью.
Вернёмся к нашей спирали. Применим к ней преобразование, которое 0 переведёт в −1, а бесконечность — в 1: r (z) = (z + 1) / (z − 1). Так как спираль заматывалась вокруг нуля, то теперь она станет заматываться вокруг −1, но ещё спираль разматывалась из бесконечности, поэтому она станет разматываться из 1.

Рассмотрим на комплексной плоскости полярную сетку и в каждую ячейку этой сетки поместим Коша.

Рассмотрим преобразование f (z) = keiφz. Оно поворачивает полярную сетку на угол φ и сжимает все клетки в k раз. Если рассмотреть последовательно несколько кадров, то получится следующее:

Если мы попытаемся уследить за каким-нибудь из Кошей, то увидим, что он движется по разматывающейся спирали, а с ней мы уже разобрались, поэтому понятно, что произойдёт, если ещё сделать преобразование r (z) = (z + 1) / (z − 1).
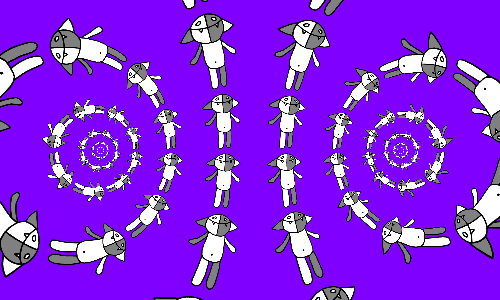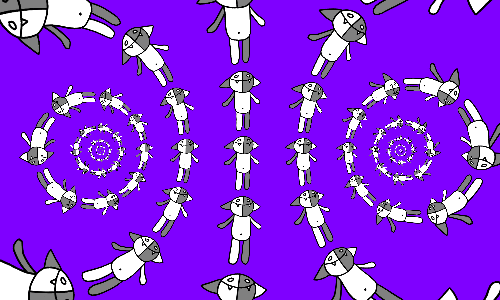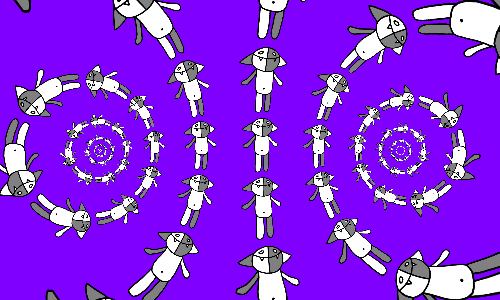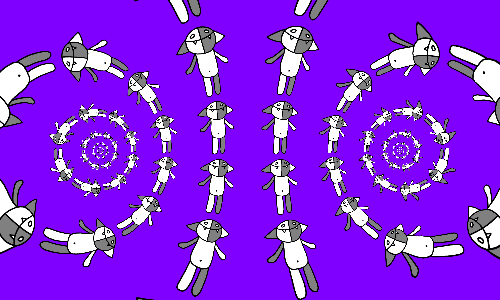
Если в каждой клетке сетки Коша положить на бок, то получим немного другую картину.

Преобразование f (z) является локсодромическим, можно также рассмотреть и преобразования других типов.
Мы разобрались с одним дробно-линейным преобразованием, теперь следует налить себе чашку вкусного чая и рассмотреть два преобразования:
a (z) = (sqrt (2)z + 1) / (z + sqrt (2)), b (z) = (sqrt (2)z + i) / (−iz + sqrt (2)).
Что делает преобразование a (z)? Разложим его в композицию f4(f3(f2(f1(z))): f1(z) = z + sqrt (2) — сдвиг на sqrt (2) вправо. f2(z) = 1 / z — инверсия относительно начала координат плюс отражение относительно действительной оси, f3(z) = −z — поворот на угол π, f4(z) = z + sqrt (2) — сдвиг на sqrt (2) вправо. Или если собрать всё вместе, то получится, что внешность единичной окружности C1 с центром в −sqrt (2) переходит во внутренность единичной окружности C2 с центром в sqrt (2), а внутренность окружности C1 во внешность окружности C2.
Преобразование a−1(z) действует, как и положено обратному преобразованию, в точности наоборот.
Аналогично действует и преобразование b (z) — только окружности C1 и C2 имеют центры в точках −isqrt (2) и sqrt (2).
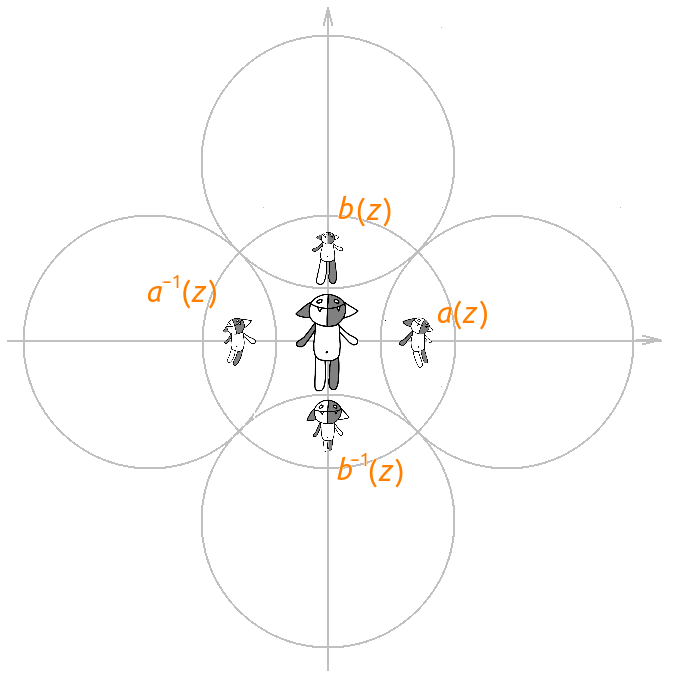
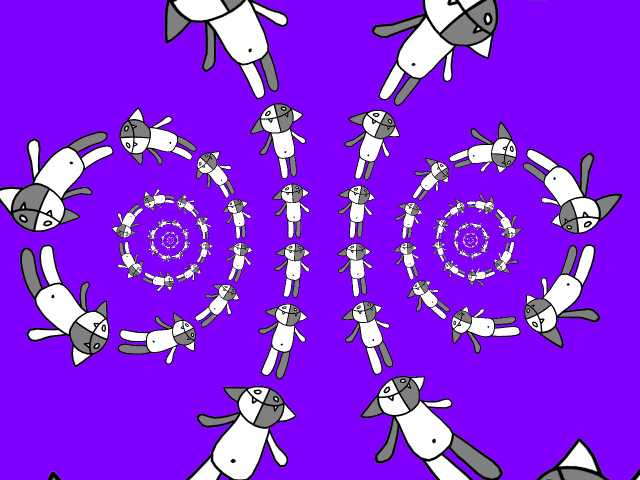
Самое время перейти к фракталам: рассмотрим всевозможные композиции отображений a (z), b (z), a−1(z) и b−1(z) и подействуем ими на Коша:

Чтобы получить гифку, снова заметим, что если к полученной картинке применить преобразование a (z) или b (z), то ничего не изменится. Рассмотрим, например, b (z): придумаем такое преобразование g (z), для которого gN (z) = b (z). Это несложно сделать, так как известно, что преобразование b (z) можно представить в виде b (z) = t−1(m (t (z))), где t (z) = (z − z1) / (z − z2), m (z) = keiφz, а z1 и z2 — неподвижные точки отображения b (z).Неподвижные точки несложно найти: решим квадратное уравнение b (z) = z и получим z1 = −i, z2 = i, откуда получаем, что m (z) = t (a (t−1(z))), следовательно, m (z) = (sqrt (2) + 1)z / (sqrt (2) − 1). Поэтому g (z) = t−1((sqrt (2) + 1)1/Nt (z) / (sqrt (2) − 1)1/N) = ((q + w)z/2 + i (q − w)/2) / (−i (q − w)z/2 + (q + w)/2)), где q = (sqrt (2) + 1)1/N, w = (sqrt (2) − 1)1/N.
Программируем и получаем:
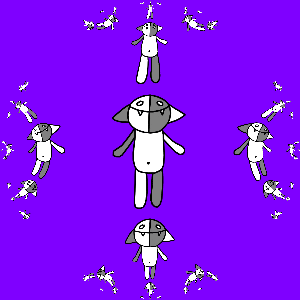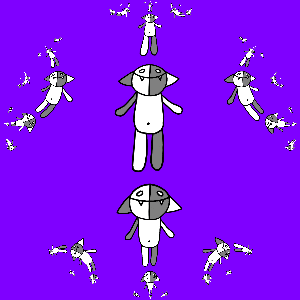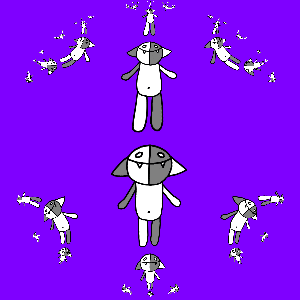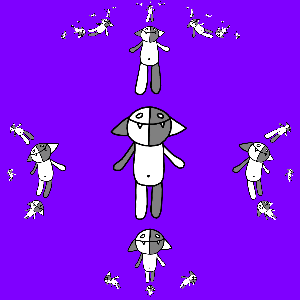
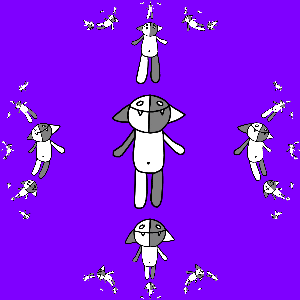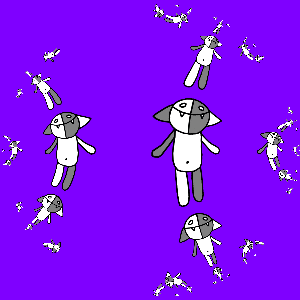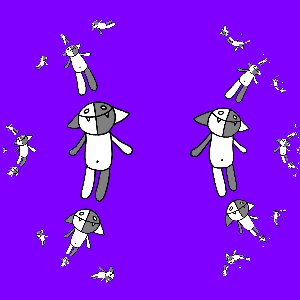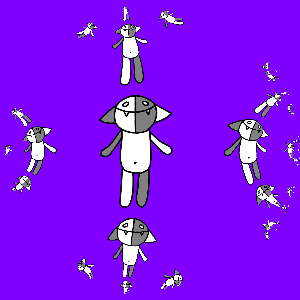
Тут интересно заметить, что преобразование g (z) оказалось автоморфизмом единичного круга.
Наконец, если сначала применить к Кошу g (z), а затем уже остальные отображения, то получится тоже неплохо:
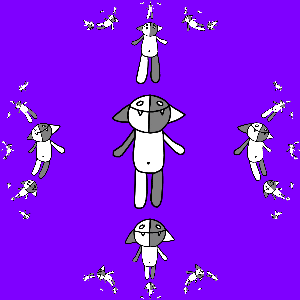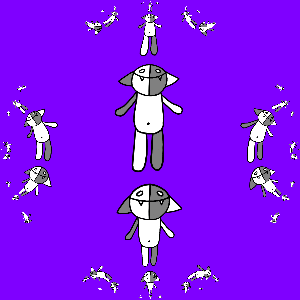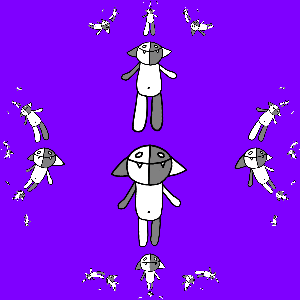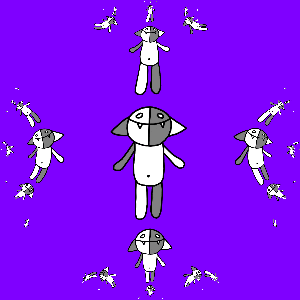
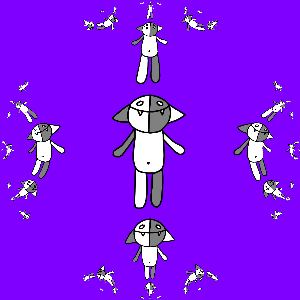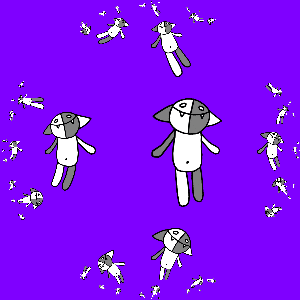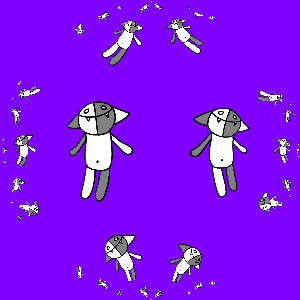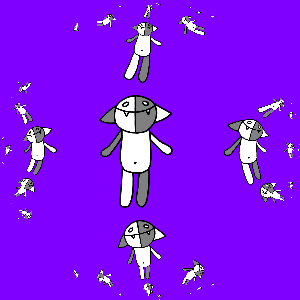
На этом всё.
Если кто-то захочет узнать больше, то рекомендую книгу Indra’s Pearls Мамфорда и др.
Если кто-то захочет поэксперементировать, то код выложен на гитхабе.
Если кто-то захочет позалипать, то можно это сделать на coub: раз и два.
