Конструирование эпидемиологических моделей
Эпидемиология из-за некоторого стечения обстоятельств стала очень популярной за последний год. Интерес к моделированию эпидемий стал возникать у многих и уже всё больше людей знают о вездесущей SIR модели. Но есть ли другие подобные модели? Насколько сложно из вообще создавать и модифицировать? Но обо всём по порядку.

За несколько месяцев до появления первых новостей о COVID-19 я для себя, так скажем, в образовательных целях программирования, начал писать программу визуализации эпидемий. В этой простой программе кружочки разных цветов двигались по полю и заражали друг друга. Через полгода, каким-то образом это уже стало темой моей дипломной работы (специальность «биоинженерия и биоинформатика») и пришлось по-настоящему вникать в математическое моделирование эпидемий для написания статей. Благо интернет вдруг стал наполняться эпидемиологическими материалами. Я это виду к тому, что работать я начал за некоторое время до того, как эпидемиология стала мейнстримом.
Прежде, чем обсуждать, свои разработки хотел рассказать немного о том, что узнал о математическом моделировании эпидемий.
Просто о SIR модели
Модель SIR, без упоминания которой не обходится почти ни одна статья по эпидемиологии, создана уже почти век назад. Она проста и элегантна, её много критикуют и много хвалят, как, собственно, любую сущность, которая применима лишь в определённых условиях и имеет свои допущения, о которых необходимо знать во время использования.
Я понимаю, что медиапространство заполнено всевозможными описаниями данной модели, поэтому я не побоюсь и добавлю ещё одно.
SIR модель. Всю популяцию, которая подвержена эпидемии, разделили на три группы: S (susceptible — восприимчивые, то есть здоровые, не заразные, но могут заразиться, так как не имеют иммунитета), I (infected — инфицированные, то есть болеют и заразны) и R (recovered — выздоровевшие, то есть здоровые, не заразные и не могут заразиться, так как имеют иммунитет). Очевидно, что до начала эпидемии 100% индивидов находятся в группе S (восприимчивые) и по нулям в остальных группах. Для удобства будем считать, популяция в 100 человек, соответственно S = 100, I = 0, R = 0. В таких условиях эпидемия, конечно, не пойдёт, так как чтобы она началась, должен быть хотя бы один больной. Поэтому рассмотри другую ситуацию: S = 99, I = 1, R = 0. Вот теперь начнётся эпидемия и её моделирование заключается в последовательном высчитывания состояния популяции на следующем шаге.
Дальше чуть сложнее, чтобы понимать сколько людей заразиться на каждом шаге, надо понимать наличие двух вероятностей: вероятность контакта между двумя индивидами и вероятность заразить при контакте инфицированного с восприимчивым (β). Часто в модели для воплощения первой вероятности используют просто 1/N (N — объём популяции), подразумевая, что в каждый момент времени каждый индивид контактирует с одним случайным индивидом в популяции. А вторая вероятность (β), обеспечивает собственно биологический показатель заразности конкретного патогена (со всеми влияющим факторами: температура, наличие маски и т.п.).
Один инфицированный встретит и заразит в конкретный момент времени конкретного восприимчивого с вероятностью:
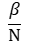
Тогда всего он заразит восприимчивых индивидов:
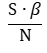
А все инфицированные вместе заразят восприимчивых
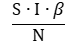
Таким образом, количество восприимчивых на втором шаге нашей модели уменьшиться на 0.99*β.
Ещё инфицированные выздоравливают, тоже с какой-то вероятностью (γ), которую часто рассматривают как число обратное времени болезни. Имеется в виду, что если болезнь длится 10 дней, то больной индивид в конкретный день выздоровеет с вероятностью γ = 1/10. Получается количество выздоравливающих на каждом шаге будет равно:
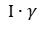
Количество инфицированных на втором шаге, помимо того, что увеличится на 0.99*β ещё уменьшится на 1*γ. Количество выздоровевших увеличится на 1*γ. Относительного полученного состояния будет высчитываться следующий шаг модели.
Таким образом модель формулируется следующими уравнениями:

Модификация SEIR
О SIR модели слышали теперь довольно многие. О существовании других моделей слышало уже меньше людей. Часто всё-таки вспоминают SEIR модель, которую рассматривают как модификацию SIR.
SEIR модель учитывает инкубационный период (E — exposed, индивиды болеют, но не заразны и со временем полностью заболеют). В такой модели заражение восприимчивых происходит таким же способом как в модели SIR, но попадают такие особи не в группу I, а в группу E. А из E с определённой вероятностью (α, число обратное длительности инкубационного периода) происходит переход уже в I.

Компартментальные модели в целом
Существует ещё много модификаций SIR моделей. Все они, включая саму SIR, являются представителями целого класса моделей, которые называют «компартментальными эпидемиологическими моделями». Упоминаемое выше разделение популяции на группы или компартменты (отсеки) как раз и обуславливает такое название моделей.
Сложность компартментальных моделей не ограничена тремя или четырьмя группами. Такие модели могут учитывать самые различные сценарии: введение карантинных мер (SIQR, добавляется группа Q — quarantine), потеря иммунитета (SIRS, переход с некоторой вероятностью из R обратно в S), группы риска у восприимчивых (несколько групп S: S1, S2, …, каждая из которых со своей вероятностью заражается), различные варианты течения болезни (несколько групп I: I1, I2, …, в каждую из которых своя вероятность попадания восприимчивых особей, а также у каждой допустим своя заразность) и т.д. Ограничением здесь является только фантазия исследователя.
Сложные схемы компартментальных моделей часто описывают в виде графа переходов. Вот, например модель для туберкулёза из книги по эпидемиологии:
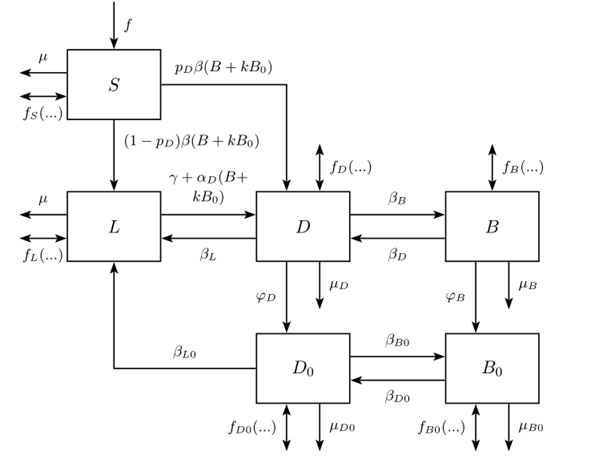 Схема распространения туберкулёза
Схема распространения туберкулёзаРеализация компартментальных моделей заключается в описании уравнений переходов и последующем расчёте изменений каждого компартмента в течение какого-то периода.
DEMMo (конструктор моделей)
В этом и заключается назначение разрабатываемой мной программы DEMMo. DEMMo — Designer of Epidemic Math Models (конструктор эпидемиологических математических моделей). Конструированные модели организуется в объектно-ориентированном виде. Есть класс стадии (аналог компартмента), класс потока (обеспечивает переход индивидов между стадиями) и внешнего потока (прибавление/вычитание индивидов к/из стадии). Подробную инструкцию по использованию программы попытался написать в документации.
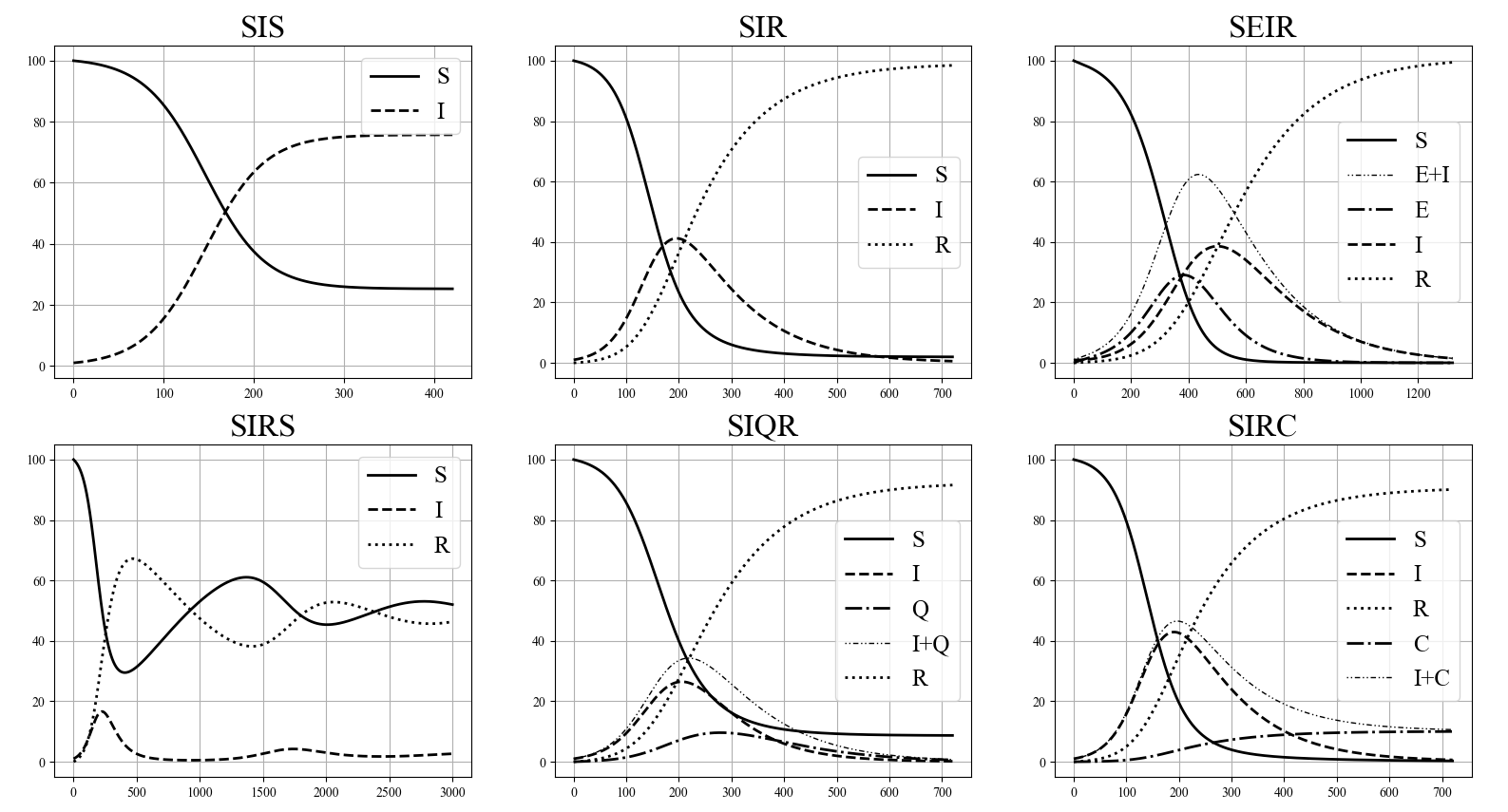 Результаты различных моделей, реализованных с использованием программы
Результаты различных моделей, реализованных с использованием программыПрограмму писал на python. Интерфейс на PyQt5. Выложил исходный код программы на github (с git работал впервые) и архив с готовой версией для windows на гугл диск. Будем считать, что начинаю бета тестирование программы. Надеюсь, я хоть немного понятно объяснил и для тех, кому интересно, буду очень рад если программу жестоко поэксплуатируют. Вроде бы настроил систему создания отчётов об ошибках. Это мой первый крупный проект после задачек на ряды Фибоначчи и т.п.
Код очень плохо задокументирован, причём часть комментариев на русском, а часть на английском. Знаю, что плохо, каюсь. Надеюсь займусь этим. Если будут какие-то конкретные советы от матёрых программистов, буду очень рад.
Контактная почта: demmo.development@gmail.com
Так уж вышло, что актуальность темы моего диплома резко возросла за последние полтора года. Надеюсь, мейнстрим никого не отпугнул и кому-нибудь было интересно и познавательно. Спасибо за внимание.
