Кодирование с изъятием информации. Часть 2-я, математическая02.01.2018 21:48

Введение


В предыдущей части рассматривалась принципиальная возможность кодирования при котором, в случае, если можно выделить общую часть у ключа и сообщения, то передавать можно меньше информации чем есть в исходном сообщении.


image

Позвольте немного расскажу откуда вообще взялась эта тема. Давным-давно от одного хорошего человека- ivlad взял почитать и вот пока никак не отдам (прости пожалуйста) интересную книжку [1], где, написано: «в свою очередь криптография сама может быть разделена на два направления, известные как перестановка и замена».

Соответственно почти сразу появились следующий вопросы:


  • т.к. перестановка и замена сохраняют количество информации, то можно ли сделать так, чтобы обойти это ограничение, и передавать информации меньше чем есть в сообщении, — отсюда (из «а не слабо ли») родилась первая часть;
  • если задача выглядит решаемой, то есть ли само решение и хотя бы толика математического смысла в нём — этот вопрос и есть тема этой части;
  • есть ли во всём этом практический смысл — вопрос пока открыт.


Что общего у ворона и письменного стола?


Загадка Кэрролла в заголовке дана как иллюстрация проблемы, которую необходимо решить. А именно: определить пару функций $E(k,m)$ — кодирования и $D(k,с)$ — декодирования, удовлетворяющих следующим условиям:


  • $I(E(k,m)) \le I(m)$ –объём передаваемой информации по Шеннону меньше объёма информации в исходном сообщении
  • $D(k,E(k,m))=m$ — функция декодирования, применённая к закодированному сообщению, позволит однозначно восстановить исходное сообщение.


Здесь $I(m)$ — объём информации по Шеннону [2] (в предположении, что все символы встречаются равновероятно, что в общем случае неверно, но для используется для простоты изложения) в сообщении $m$, $k$ — ключ, $с = E(k,m)$ — закодированное сообщение.


Для того, чтоб упростить себе дальнейшие рассуждения давайте ограничимся в дальнейшем сообщениями, которые можно привести в числовую форму, что с одной стороны нас не особо ограничивает (т.к. любому символу можно присвоить соответствующий числовой код), а с другой позволит воспользоваться математикой в нужном объёме.


Итак, рассмотрим сначала для примера два числа $k= 746 130$ и $m = 50 133 666$ и, воспользовавшись основной теоремой арифметики [4] (любое натуральное можно разложить на произведение простых) найдём следующие параметры:


  • Наименьший общий делитель $k$ и $m$ — $НОД(k,m) = 1 254$, его простые делители $[2,3,11,19]$,
  • Частное $m/НОД(k,m) = 595$ и его простые делители $[5,7,17]$, которое обозначим как $с_0$,
  • Разложение числа $m$ на простые множители: $[2,3,11,19, 39 979]$,
  • Разложение числа $k$ на простые множители: $[2,3,5,7,11,17,19]$.


Запишем всё это в табличном виде, где синим помечена общая часть информации между ключом и сообщением, жёлтым — информация уникальная для ключа, оранжевым — уникальная для сообщения:


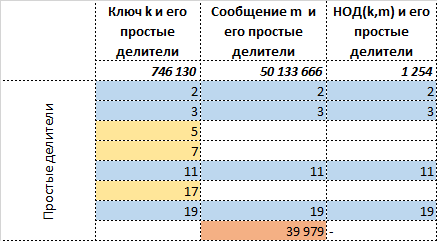
image

Сразу же становится видно, что $НОД(k,m)$ представляет из себя общую часть между ключом $k$ и сообщением $m$, которая есть и у отправителя и у получателя. Таким образом, в идеале конечно, а не в реальности, достаточно передать информацию об:

  • уникальной для сообщения информации — том, что не относится к $k$ т.е. $[39 979]$, а именно $с_0 = 39 979$,


  • самом $НОД(k,m)$, но так, чтобы его нельзя было бы восстановить.


Пометим теперь позиции простых делителей $НОД(k,m)$ общие с простыми делителями $k$, единицами, а остальные, кроме, может быть ведущей позиции — нулями.


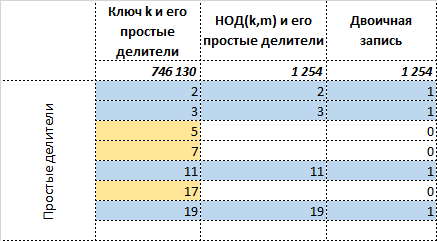
image

Получившееся число $с_1 = 1010011 = 83$ в достаточной степени характеризует $НОД$, позволяя тем самым восстановить исходное сообщение. Т.е. получив на вход два числа $[39 979, 83]$ необходимо сделать достаточно простое обратное преобразование:

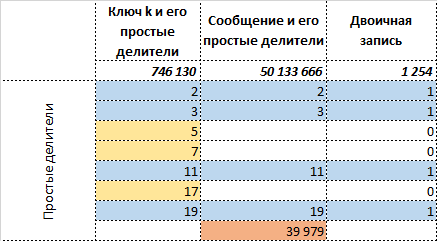
image

Если теперь оценить длину исходного сообщения в двоичном виде $len_2(m) = len_2([1111010000011100100000100])= 26$ и сообщения $len_2([c_0,c_1])= len_2([1001110000101011, 1010011]) = 23$, то видно, что можно получить экономию длины сообщения в $3$ бита, то же самое и с количеством информации $I(m) = 13$ бит, $I(c)=I([c_0,c_1])=11.5$ бита. Здесь функция $len_2(\cdot)$ — длина числа в двоичном виде.

image

Таким образом, выражаясь словами из известного анекдота «в Шотландии есть как минимум одна овца, черная как минимум с одной стороны» [3].

Итак, что на данный момент имеем — данный способ кодирования подходит, но только для пар чисел, имеющих в разложении одинаковые делители. В противном случае, если, например, взять в качестве ключа и в качестве сообщения простые числа, то очевидным образом мы ничего сократить не сможем, а только увеличим и длину сообщения, как и количество передаваемой информации, а это вовсе не то, чего добивались. Эта же ситуация повторяется и в случае когда, например, $НОД(k,m)<2$ или же $len_2(c_1)≥ len_2(НОД(k,m))$ т.к. экономия будет либо минимальной либо будет отсутствовать в принципе.

Что делать…


для того, чтобы повысить вероятность успеха при таком способе кодирования?
В общем-то если внимательно посмотреть на ключ, то видно, что он неплохо делится на простые числа $2,3,5,7,11,17,19$, что сделано специально для успешности операции нахождения $НОД(k,m)$. Так как такая операция негативно может повлиять на количество используемых ключей, то определяя порядок следования простых множителей и сделав его частью ключевой информации, получим, хоть и не радикальное, но увеличение количества вариантов кодирования, что положительным образом отразиться на количестве ключей. Использовав вместо ключа не число $[746 130]$, а пару $[746 130, 0125763]$, где второе число отражает порядок перемножения и определяет значение $c_1$.


Следующая проблема, которую предстоит эффективно решить — соотношение частот появления простых чисел и степеней двойки, -легко заметить, что эффективность кодирования степенями двойки довольно быстро падает с ростом длины $c_1$ (см. график соответствующих последовательностей если есть один общий простой делитель) и зависит в основном от количества делителей ключа и их значений.


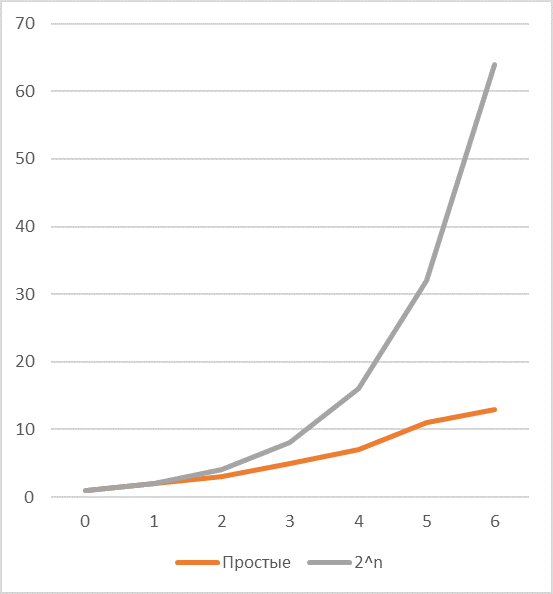
image

В случае если, общих делителей два и один из них, например, равен $3$, то возможности по экономии возрастают весьма заметно.

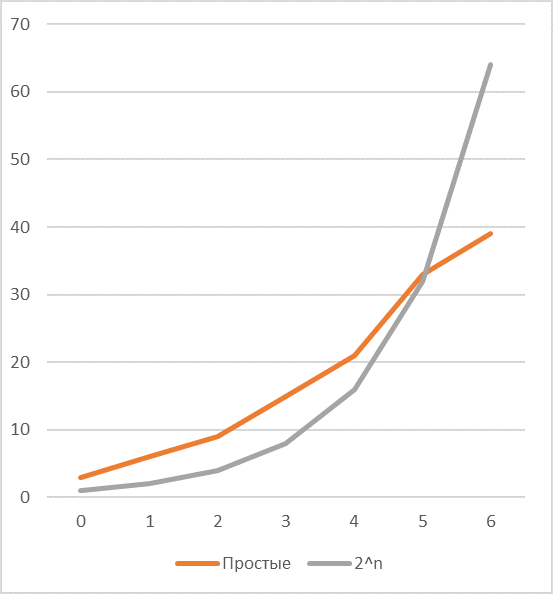
image

Что означает, что для эффективного кодирования необходимо придумать более эффективный способ кодирования $c_1$.

То есть тему есть смысл прокапывать дальше.


Пример


Как обычно выложены на github [5] — используется Excel т.к. он есть у многоих и нет необходимости думать о совместимости. В файле две закладки:


  • «Тест» — сами вычисления и т.к. в них довольно активно используется функция Excel «СЛУЧМЕЖДУ ()» и числа ключа и сообщения могут оказаться взаимно простые, то придётся несколько раз встать в какую либо ячейку и нажать enter для того, чтобы получить искомую экономию (результаты в строчках 31–36);
  • «Пример 1» — приведены примеры готовых вычислений, т.к. случайность в excel не оставляет им шанса на повторение.


Ссылки


  1. Сингх Саймон. Книга шифров. Тайная история шифров и их расшифровки. М. Астрель 2007.
  2. https://ru.wikipedia.org/wiki/%D0%98%D0%BD%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%86%D0%B8%D0%BE%D0%BD%D0%BD%D0%B0%D1%8F_%D1%8D%D0%BD%D1%82%D1%80%D0%BE%D0%BF%D0%B8%D1%8F
  3. http://www.gaelic.ru/Biblioteka/Folklore/anekdoty.htm
  4. https://ru.wikipedia.org/wiki/%D0%9E%D1%81%D0%BD%D0%BE%D0%B2%D0%BD%D0%B0%D1%8F_%D1%82%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D0%B0_%D0%B0%D1%80%D0%B8%D1%84%D0%BC%D0%B5%D1%82%D0%B8%D0%BA%D0%B8
  5. https://github.com/rumiantcev/nod_code

© Habrahabr.ru