Клеточные автоматы. Игра «Жизнь». Часть 125.05.2023 22:31

0. Как я познакомился с клеточными автоматами

В начале 2022 года я, обычный студент 4 курса с направления «Радиофизика», вместо того, чтобы постигать труды по ТОЭ и радиоэлектронике, смотрел YouTube в поисках интересного контента. Меня очень увлекала занимательная математика и головоломки, поэтому я был подписан на множество каналов про околонаучные темы, в том числе по программированию. Мне в ленте попалось потрясающее видео с канала «Onigiri», я всем советую ознакомится с ним, чтобы лучше погрузиться в контекст. Оно сделано очень качественно и очаровывает своим простым повествованием, при этом то, что происходит на экране очень увлекает!

Посмотрите на досуге, а пока, чтобы не отвлекаться, я вам кратко опишу о чем же рассказывают в этом видео.

1. Автоматы которые не стреляют

Представьте перед собой тетрадный лист в клетку. И для начала возьмем простой карандаш и закрасим несколько десятков клеток на этом листе. Дальше немного поиграем, правила очень просты:

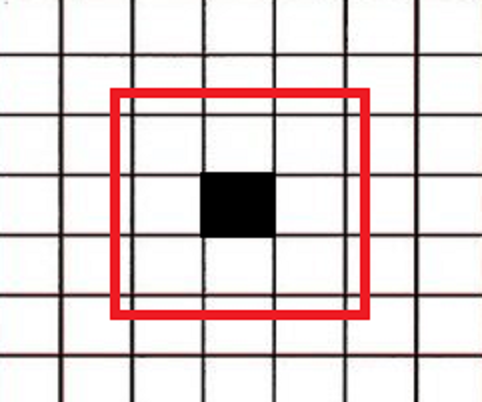
Закрашенная клетка и ее 8 соседей.

• Если клетка закрашена, то мы ее оставим закрашенной только если у нее 2 или 3 закрашенных соседа. В остальных случаях, к примеру, как на рисунке, клетку нужно стереть.

• Если клетка не закрашена, то мы ее закрасим только если рядом у нее 3 закрашенных соседа.

• Повторим для каждой клетки (лучше брать небольшой листочек, а то можно быстро устать) и увидим, что наш рисунок уже отличается от начального.

• Таких проходов можно сделать сколько угодно и каждый раз наш рисунок на листке будет меняться, то есть наша картинка эволюционирует по обозначенным нами правилам.

Можно сказать, что клетка «рождается», когда соседа 3, «выживает», когда соседей 2 или 3, а в остальных случаях либо «умирает», либо вообще «не рождается». Поэтому такие правила для игры назвали B3/S23, B — Born в переводе с английского «рождение», а S — Survival, что значит «выживание».

В такую игру можно надолго залипнуть на листочке, но спустя время появляется желание побаловаться с этим на компьютере, так как уж больно долго делать все это от руки, поэтому надо автоматизировать!

2. Простенький код с пояснениями

Если вы никогда не программировали, то это отличный повод начать, хоть для совсем начинающих это будет сложно, но я все равно постараюсь написать подробно про каждую строку кода, благо их надо совсем чуть-чуть. Я буду использовать язык Python просто потому, что умею писать только на нем! :)

Итак, нам понадобиться сделать анимацию нашего тетрадного листа, будто компьютер быстро закрашивает и стирает клетки по нужным правилам. Для такой анимации я буду использовать библиотеку matplotlib. Библиотека matplotlib это просто код, который написали другие добрые и умные люди, он содержит функции, которые помогают строить различные графики, в том числе и анимировать их. Также, я хочу в начале случайно закрасить какие-то клетки, значит мне нужна функция для генерации случайных значений. Для этих целей я всегда использую библиотеку numpy, там есть такая функция.

Подключаем наши библиотеки:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

Заметьте, что я импортирую два модуля из библиотеки matplotlib это pyplot, который и будет строить график, а также animation, который будет его анимировать. Вы спросите, откуда я знаю, что мне нужны такие модули. Все модули и их функции описаны в документации к библиотеке:

https://matplotlib.org/stable/users/index.html

Дальше я введу переменные для нашей программы:

N = 50
ON = 255
OFF = 0
vals = [ON, OFF]

N = 50: Это размерность игровой сетки (нашего листка в клетку). Я для простоты сделаю квадратный листок N*N, то есть у нас будет 50 клеток в длину и 50 в ширину.

ON = 255, OFF = 0: Эти две строки определяют состояния клеток. «Живая» клетка, она же ON, будет иметь значение 255, а «мертвая», она же OFF, будет иметь значение 0. Вы спросите, что за странные значения, ведь было бы логичнее выбрать 1 и 0. 1 — клетка жива, 0 — мертва. Все дело в библиотеке matplotlib. Значение 255 будет отображаться как белый цвет, а 0 — как черный.

vals = [ON, OFF]: Это просто список, содержащий два возможных состояния клетки — ON и OFF. Этот список используется при инициализации игровой сетки случайными значениями. То есть мы просто возьмем функцию для случайных значений и попросим разбросать случайным образом значения из этого списка по полю N*N.

Сделать это проще, чем кажется. Введем переменную grid, что значит «сетка» с английского. В нее мы положим результат выполнения той самой функции, которая будет случайным образом выбирать значения из списка vals для заполнения нашего поля N*N: np.random.choice:

grid = np.random.choice(vals, N*N, p=[0.2, 0.8])

Но вы видите, что я добавил ещё p=[0.2, 0.8]. Параметр p=[0.2, 0.8] задаёт вероятности выбора соответствующих состояний. То есть, есть 20% вероятности, что клетка будет в состоянии ON (живая), и 80% вероятности, что клетка будет в состоянии OFF (мертвая). Я выбрал именно такие значения просто так, можно экспериментировать с этим параметром, как и с величиной сетки. Это может быть полезно для создания более интересных и разнообразных начальных конфигураций. Если бы вы установили p=[0.5, 0.5], то у вас было бы равное количество «живых» и «мертвых» клеток в начальной конфигурации. Или, если бы вы установили p=[0.9, 0.1], большинство клеток были бы «живыми».

Друзья, также есть ещё один интересный момент. Функция np.random.choice вернет нам одномерный массив длиной N*N, а мы то помним, что нам нужен двумерный клеточный листок, значит надо превратить этот одномерный массив в двумерный массив (то есть в сетку, листок). Для этого просто допишем к нашей строке ещё одну функцию: reshape (N, N):

grid = np.random.choice(vals, N*N, p=[0.2, 0.8]).reshape(N, N)

Теперь у нас есть клеточный листок с изначальными закрашенными («живыми») и не закрашенными («мертвыми») клетками. Настал самый интересный момент, как заставить их эволюционировать по нашим правилам? Давайте для этого напишем собственную функцию, хотя я уверен, что есть библиотеки, в которых это уже реализовано, но также совсем неинтересно, верно? :)

Мы сделаем такую функцию, которую будем вызывать каждый раз, когда нужно изменить состояние наших клеток на листке. То есть мы вызываем функцию, она обновляет сетку по вышеописанным правилам, а затем выводит на экран. И так мы делаем как бы «мультик» кадр за кадром выводя новое состояние сетки.

Определим нашу функцию:

def update(data):

Дальше скажем интерпретатору, что хотим использовать уже имеющуюся у нас сетку, а она у нас лежит в глобальной переменной grid (то есть вне какой-либо функции):

global grid

Создаем копию текущего состояния сетки. Мы будем изменять newGrid, а не исходную сетку grid, чтобы не влиять на наши расчеты в процессе обновления:

newGrid = grid.copy()

Дальше нам нужно пройтись по каждой клетке в каждой строке нашей сетки, для этого будем использовать простейший двойной цикл, где i номер строки из N, а j номер клетки из N:

for i in range(N):
  for j in range(N):

Для каждой клетки мы должны знать кол-во живых соседей вокруг нее, для этого введем переменную total, которая и будет отражать это число:

total = (grid[i, (j-1)%N] + grid[i, (j+1)%N] +
         grid[(i-1)%N, j] + grid[(i+1)%N, j] +
         grid[(i-1)%N, (j-1)%N] + grid[(i-1)%N, (j+1)%N] +
         grid[(i+1)%N, (j-1)%N] + grid[(i+1)%N, (j+1)%N])/255

Не смотрите на кажущуюся сложность этого выражения, на самом деле все очень просто:

• Первое, что мы учли в этом выражении — листок прямоугольный, а значит краевые клетки не всегда имеют 8 соседних, как мы договаривались. И чтобы исправить это мы свернем наш листок так, чтобы у краевых клеток всегда были соседи. Поверхность, где края нашей сетки будут соединяться с противоположными, создавая бесшовное пространство без границ — тор. Мы можем свернуть наш прямоугольник в тор!

  Сначала прямоугольник может свернуться в цилиндр (две параллельные стороны прямоугольника смыкаются). Затем цилиндр может свернуться в тор (оставшиеся стороны цилиндра смыкаются).

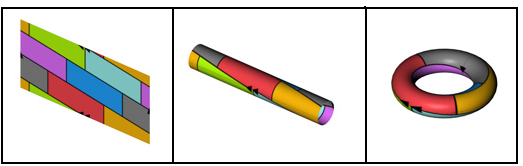
Геометрическое представление образования тора из прямоугольника.

• Это геометрическое превращение мы проделываем с помощью всего одной операции — %N. Оператор % в Python — это оператор модуля, который возвращает остаток от деления. Оператор %N возвращает остаток от деления на N, где N — размер сетки. Но как это работает?

  Давайте разберем это на конкретном примере. Предположим, что у нас есть сетка размером 5×5 (N = 5). Если мы взглянем на клетку с индексом (0,0) (верхний левый угол), то у нас есть соседи вверху и слева. Но, так как это край сетки, кажется, что соседей нет:

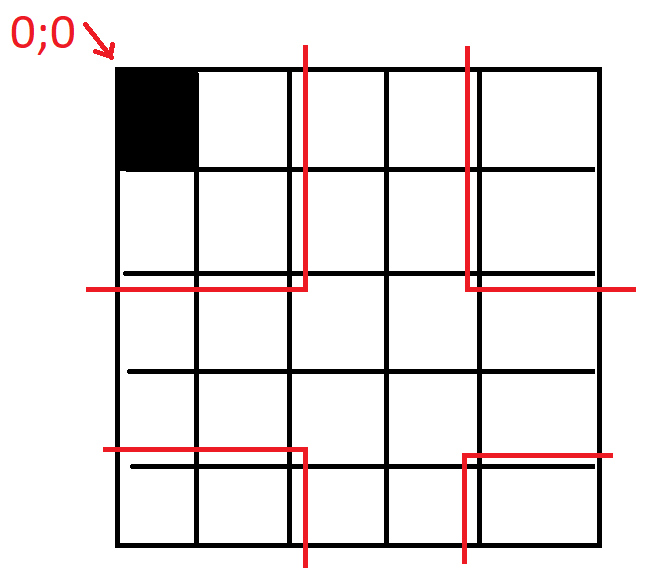
Пример поиска соседей для клетки с индексом (0, 0)

• Мы хотим обратиться к ее соседу слева, чтобы проверить «мертв» он или «жив», индекс этого соседа будет (0, -1). Однако в Python отрицательные индексы интерпретируются как обращение к элементам с конца массива, поэтому (0, -1) будет ссылаться на последний элемент в нулевой строке, что является желаемым поведением в этом случае. Но что будет в таком случае?

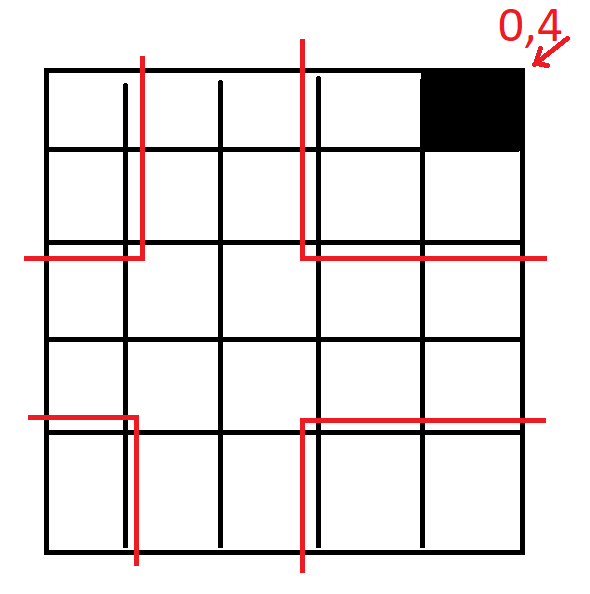
Пример поиска соседей для клетки с индексом (0,4)

• Мы хотим обратиться к соседу справа, чтобы также его проверить, но он уже будет иметь индекс (0, 5) (так как grid[i, (j+1)]), что говорит о том, что мы вышли за пределы цикла, потому что для сетки размером N цикл будет проходить значения от 0 до N-1. Вспомним:

for i in range(N):
  for j in range(N):

• И что делать? Python даст ошибку IndexError, а проверить соседей справа как-то надо. Тут и приходит на помощь %N:

  Мы делим наш j-ый индекс на N = 5 и смотрим на остаток от деления (grid[i, (j+1)%N), в этом случае он ноль — 5/5 = 1, остаток = 0. И получаем индекс (0,0), именно тот, который нам нужен!

  То есть при обращении к соседям справа или внизу от клетки на правом или нижнем краю сетки, мы получим индексы, превышающие размер сетки. В этих случаях, (i+1)%N или (j+1)%N вернут нам индекс 0, что также является желаемым поведением. Это наконец-то делает индексацию «циклической», или «тороидальной», как мы обсуждали ранее. Мы свернули прямоугольник в тор!

• Второе, что мы учли, что все «живые» клетки обозначаются значением 255, поэтому чтобы получить число «живых» клеток в переменной total нужно будет поделить полученную сумму на 255.

После того, как мы посчитали всех «живых» соседей нашей клетки, напишем простое логическое выражение, которое вводило бы наши правила игры в программу:

if grid[i, j]  == ON:
  if (total < 2) or (total > 3):
    newGrid[i, j] = OFF
else:
  if total == 3:
    newGrid[i, j] = ON

Разберем построчно:

if grid[i, j]  == ON

1) Если клетка жива

if (total < 2) or (total > 3)

2) И если у нее меньше 2 или больше 3 «живых» соседей

newGrid[i, j] = OFF

3) То в новом «кадре» нашей анимации мы ее «убьем»

else:

4) Иначе, если клетка «мертва»

if total == 3

5) И если у нее ровно 3 «живых» соседа

newGrid[i, j] = ON

6) То в новом «кадре» нашей анимации мы ее «возрадим».

Вот и готова наша игра! Теперь за пределами цикла, после того как мы обработали все клетки, мы заменяем старую сетку новой:

grid = newGrid

И последняя волшебная команда:

mat.set_data(grid)

Эта операция обновляет данные в объекте mat, который используется для визуализации сетки на графике. Это обновление заставит matplotlib отобразить новое состояние сетки при следующем кадре анимации.

А теперь сделаем так, чтобы наша функция вернула этот объект:

return [mat]

Эта строка возвращает список из одного элемента — объекта mat, который был обновлен на предыдущей строке. Это нужно для функции FuncAnimation из matplotlib.animation, которая ожидает, что функция обновления вернет список объектов, которые были изменены.

Именно из-за FuncAnimation мы определили функцию в начале с входной переменной data. Коротко говоря, data включается в определение функции update для совместимости с FuncAnimation, даже если оно не используется.

Функция для эволюции наших клеток на листочке готова, переходим к созданию анимации!

fig, ax = plt.subplots()

Эта строка создает новый график, используя функцию subplots из matplotlib.pyplot. Эта функция возвращает два объекта: Figure (здесь сохраняется как fig) и Axes (здесь сохраняется как ax). Figure — это весь график, а Axes — это область графика, где данные отображаются.

Как вы понимаете, теперь надо передать в Axes наши данные после обновления сетки — grid:

mat = ax.matshow(grid)

Мы применяем к Axes функцию matshow () и в нее передаем нашу новую сетку grid, тем самым говорим, чтобы функция matshow () преобразовала наш массив так, чтобы он превратился в объект AxesImage, который можно отобразить уже в Axes. И мы уже готовый объект для отображения устанавливаем в переменную mat.

График готов, кадр анимации тоже, теперь просто поместим все это в одну функцию:

ani = animation.FuncAnimation(fig, update, interval=50, save_count=50)

Как мы уже указывали это функция FuncAnimation из модуля animation. Туда мы передаем наш график fig, функцию для обновления анимации update и два параметра:

• Параметр interval=50 указывает, что между кадрами анимации должен быть интервал в 50 миллисекунд, а save_count=50 указывает, что должно быть сохранено 50 кадров анимации. Увеличение interval замедлит вашу анимацию, так как будет больше времени между кадрами, в то время как уменьшение interval ускорит вашу анимацию.

• Увеличение save_count может привести к большему использованию памяти, но позволит сохранить больше кадров, если вы решите сохранить анимацию в файл.

И последняя главная команда, чтобы посмотреть результат наших стараний на экране компьютера:

plt.show()

Результат нашей кропотливой работы!

Gif-ку сделал вот так:

ani = animation.FuncAnimation(fig, update, interval=40, save_count=1000)
ani.save('game_of_life.gif', writer='pillow', fps=25)

Только учтите важный момент — для создания GIF вам также потребуется установить ImageMagick или Pillow. Я использую Pillow, так как его легко установить через командную строку Python:

pip install pillow

3. Игра «Жизнь».

Приглядитесь внимательнее, мы с вами с нуля сделали целую симуляцию! 30 строк кода, а на экране возникает целая жизнь! Наша игра на листке бумаги переросла в колонии клеток, которые размножаются, перемещаются, убивают друг друга. Здесь много интересных структур, которые возникают в процесс эволюции нашей «популяции» клеток, включая некоторые, которые могут двигаться по сетке («космические корабли») и другие, которые генерируют новые клетки в регулярных интервалах («генераторы»). Если вам интересно, то я обязательно расскажу о них максимально подробно в следующих статьях.

То, что мы с вами получили называется клеточный автомат! В общем случае клеточный автомат — дискретная динамическая математическая модель, состоящая из регулярной решетки, но размерность решетки, форма, правила эволюции, соседи, все это многообразие параметров не установлено заранее. И вы даже не представляете, что в себе несет такая простая математическая модель.

Мы запрограммировали всего один достаточно простой частный случай клеточного автомата, который называется «Игра «Жизнь». Эту игру придумал английский математик Джон Конвей в 1970 году, он с детства вдохновлялся трудами Джона Фон Неймана, который придумал концепт клеточного автомата. И хоть гений Фон Неймана дал жизнь клеточным автоматам, его правила были достаточны сложны для обывателей, а вот Конвей изначально ставил себе цель сделать максимально простой по правилам клеточный автомат, но при этом с нетривиальным поведением, также он хотел добиться полноты по Тьюрингу. Простыми словами это значит, что на таком клеточном автомате можно реализовать любую функцию, даже сам клеточный автомат (да, игра в жизнь внутри игры в жизнь). Кстати, такие умельцы нашлись:

Полнота по Тьюрингу дает возможность воссоздать даже маленький компьютер:

Весь секрет заключается в том, чтобы найти нужную начальную конфигурацию клеточного автомата (а мы начальную конфигурацию делали случайным образом). Надо ли говорить, что это очень сложная задача!

«Жизнь» оказалась удачным выбором и быстро стала популярной из-за своей простоты и интересных визуальных эффектов.

4. Продолжение следует…

Друзья, я большой фанат клеточных автоматов и если вам понравилась моя статья про игру «Жизнь», то напишите об этом, и я обязательно расскажу ещё много интересного про эти удивительные математические структуры.

Полный код клеточного автомата вы сможете найти на GitHub

Спасибо за ваше внимание! До новых встреч!

Александр Глебов

© Habrahabr.ru