Как уменьшить количество измерений и извлечь из этого пользу
Сначала я хотел честно и подробно написать о методах снижения размерности данных — PCA, ICA, NMF, вывалить кучу формул и сказать, какую же важную роль играет SVD во всем этом зоопарке. Потом понял, что получится текст, похожий на вырезки из опусов от Mathgen, поэтому количество формул свел к минимуму, но самое любимое — код и картинки — оставил в полном объеме.
Еще думал написать об автоэнкодерах. В R же, как известно, беда с нейросетевыми библиотеками: либо медленные, либо глючные, либо примитивные. Это и понятно, ведь без полноценной поддержки GPU (и в этом огромный минус R по сравнению с Python) работа со сколь-нибудь сложными нейронными сетями — и в особенности с Deep Learning — практически бессмысленна (хотя есть подающий надежды развивающийся проект MXNet). Интересен также относительно свежий фреймворк h2o, авторов которого консультирует небезызвестный Trevor Hastie, а Cisco, eBay и PayPal даже используют его для создания своих планов по порабощению человечества. Фреймворк написан на Java (да-да, и очень любит оперативную память). К сожалению, он тоже не поддерживает работу с GPU, т.к. имеет несколько иную целевую аудиторию, но зато отлично масштабируется и предоставляет интерфейс к R и Python (хотя любители мазохизма могут воспользоваться и висящем по дефолту на localhost:54321 web-интерфейсом).
Так вот, если уж возник вопрос о количестве измерений в наборе данных, то это значит, что их, ну, скажем так, довольно много, из-за чего применение алгоритмов машинного обучения становится не совсем удобным. А иногда часть данных — всего лишь информационный шум, бесполезный мусор. Поэтому лишние измерения желательно убрать, вытащив из них по возможности все самое ценное. Кстати, может возникнуть и обратная задача — добавить еще измерений, а попросту — больше интересных и полезных фич. Выделенные компоненты могут быть полезны и для целей визуализации (t-SNE на это, например, и ориентирован). Алгоритмы декомпозиции интересны и сами по себе в качестве машинных методов обучения без учителя, что, согласитесь, иногда может и вовсе привести к решению первичной задачи.
Матричные разложения
В принципе, для сокращения размерности данных с той или иной эффективностью можно приспособить большинство методов машинного обучения — этим, собственно, они и занимаются, отображая одни многомерные пространства в другие. Например, результаты работы PCA и K-means в некотором смысле эквивалентны. Но обычно хочется сокращать размерность данных без особой возни с поиском параметров модели. Самым важным среди таких методов, конечно же, является SVD. «Почему SVD, а не PCA?» — спросите вы. Потому что SVD, во-первых, само по себе является отдельной важной методикой при анализе данных, а полученные в результате разложения матрицы имеют вполне осмысленную интерпретацию с точки зрения машинного обучения; во-вторых, его можно использовать для PCA и с некоторыми оговорками для NMF (как и других методов факторизации матриц); в-третьих, SVD можно приспособить для улучшения результатов работы ICA. Кроме того, у SVD нет таких неудобных свойств, как, например, применимость только к квадратным (разложения LU, Schur) или квадратным симметричным положительно определенным матрицам (Cholesky), или только к матрицам, элементы которых неотрицательны (NMF). Естественно, за универсальность приходится платить — сингулярное разложение довольно медленное; поэтому, когда матрицы слишком большие, применяют рандомизированные алгоритмы.
Суть SVD проста — любая матрица (вещественная или комплексная) представляется в виде произведения трех матриц:
X=UΣV*,
где U — унитарная матрица порядка m; Σ — матрица размера m x n, на главной диагонали которой лежат неотрицательные числа, называющиеся сингулярными (элементы вне главной диагонали равны нулю — такие матрицы иногда называют прямоугольными диагональными матрицами); V* — эрмитово-сопряжённая к V матрица порядка n. m столбцов матрицы U и n столбцов матрицы V называются соответственно левыми и правыми сингулярными векторами матрицы X. Для задачи редукции количества измерений именно матрица Σ, элементы которой, будучи возведенными во вторую степень, можно интерпретировать как дисперсию, которую «вкладывает» в общее дело каждая компонента, причем в убывающем порядке: σ1 ≥ σ2 ≥… ≥ σnoise. Поэтому-то при выборе количества компонент при SVD (как и при PCA, между прочим) ориентируются именно на сумму дисперсий, которую дают учитываемые компоненты. В R операцию сингулярной декомпозиции выполняет функция svd (), которая возвращает список из трех элементов: вектора d c сингулярными значениями, матриц u и v.
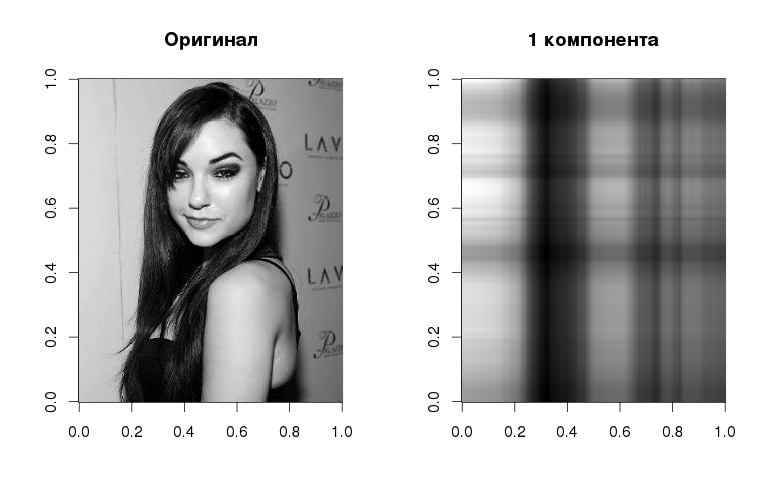
Да, так выглядит Саша в серых полутонах со всего лишь одной компонентой, но и тут можно разглядеть базовую линеаризованную структуру — в соответствии с градациями на исходном изображении. Сама компонента получается, если умножить левый сингулярный вектор на соответствующие ему сингулярное значение и правый сингулярный вектор. По мере увеличения количества векторов растет и качество реконструкции изображения:
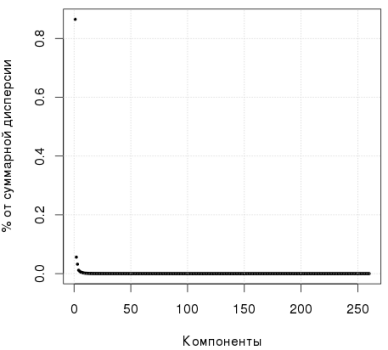
На следующем графике видно, что первая компонента объясняет более 80% дисперсии:
library(jpeg)
img <- readJPEG("source.jpg")
svd1 <- svd(img)
# Первая компонента
comp1 <- svd1$u[, 1] %*% t(svd1$v[, 1]) * svd1$d[1]
par(mfrow=c(1,2))
image(t(img)[,nrow(img):1], col=gray(0:255 / 255), main="Оригинал")
image(t(comp1)[,nrow(comp1):1], col=gray(0:255 / 255), main="1 компонента")
# Несколько компонент
par(mfrow=c(2,2))
for (i in c(3, 15, 25, 50)) {
comp <- svd1$u[,1:i] %*% diag(svd1$d[1:i])%*% t(svd1$v[,1:i])
image(t(comp)[,nrow(comp):1], col=gray(0:255 / 255), main=paste0(i," компонент(ы)"))
}
par(mfrow=c(1,1))
plot(svd1$d^2/sum(svd1$d^2),pch=19,xlab="Компоненты",ylab="% от суммарной дисперсии", cex=0.4)
grid()
Что будет, если из исходного изображения вычесть средние значения каждого столбца, разделить полученную матрицу на корень квадратный из количества столбцов в исходной матрице, а потом выполнить сингулярное разложение? Оказывается, что столбцы матрицы V в полученном разложении в точности будут соответствовать главным компонентам, которые получаются при PCA (к слову, в R для PCA можно использовать функцию prcomp ())
> img2 <- apply(img, 2, function(x) x - mean(x)) / sqrt(ncol(img))
> svd2 <- svd(img2)
> pca2 <- prcomp(img2)
> svd2$v[1:2, 1:5]
[,1] [,2] [,3] [,4] [,5]
[1,] 0.007482424 0.0013505222 -1.059040e-03 0.001079308 -0.01393537
[2,] 0.007787882 0.0009230722 -2.512017e-05 0.001324682 -0.01373691
> pca2$rotation[1:2, 1:5]
PC1 PC2 PC3 PC4 PC5
[1,] 0.007482424 0.0013505222 -1.059040e-03 0.001079308 -0.01393537
[2,] 0.007787882 0.0009230722 -2.512017e-05 0.001324682 -0.01373691
Таким образом, при выполнении сингулярного разложения нормализованной исходной матрицы не составляет труда выделить главные компоненты. Это и есть один из способов их вычисления; второй же основывается непосредственно на поиске собственных векторов ковариационной матрицы XXT.
Вернемся к вопросу выбора количества главных компонент. Капитанское правило такое: чем больше компонент, тем больше дисперсии они описывают. Andrew Ng, например, советует ориентироваться на >90% дисперсии. Другие исследователи утверждают, что это число может быть и 50%. Даже придуман так называемый параллельный анализ Хорна, который основывается на симуляции Монте-Карло. В R для этого и пакет есть. Совсем простой подход — использовать scree plot: на графике надо искать «локоть» и отбрасывать все компоненты, которые формируют пологую часть этого «локтя». На рисунке ниже, я бы сказал, надо учитывать 6 компонент:
В общем, как вы видите. вопрос неплохо проработан. Также бытует мнение, что PCA применим только для нормально распределенных данных, но Wiki с этим не согласна, и SVD/PCA можно использовать с данными любого распределения, но, конечно, не всегда результативно (что выясняется эмпирически).
Еще одно интересное разложение — это факторизация неотрицательных матриц, которая, как следует из названия, применяется для разложения неотрицательных матриц на неотрицательные матрицы:
X=WH.
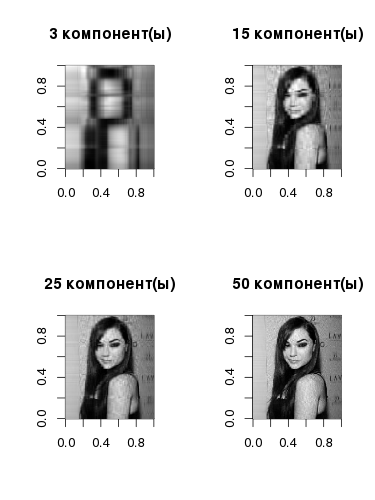
В целом, такая задача не имеет точного решения (в отличие от SVD), и для ёё вычисления используют численные алгоритмы. Задачу можно сформулировать в терминах квадратичного программирования — и в этом смысле она будет близка к SVM. В проблеме же сокращения размерности пространства важным является вот что: если матрица Х имеет размерность m x n, то соответственно матрицы W и H имеют размерности m x k и k x n, и, выбирая k намного меньше самих m и n, можно значительно урезать эту самую исходную размерность. NMF любят применят для анализа текстовых данных, там, где неотрицательные матрицы хорошо согласуются с самой природой данных, но в целом спектр применения методики не уступает PCA. Разложение первой картинки в R дает такой результат:
library(NMF)
par(mfrow=c(2,2))
for (i in c(3, 15, 25, 50)) {
m.nmf <- nmf(img, i)
W <- m.nmf@fit@W
H <- m.nmf@fit@H
X <- W%*%H
image(t(X)[,nrow(X):1], col=gray(0:255 / 255), main=paste0(i," компонент(ы)"))
}
Если требуется что-то более экзотичное
Есть такой метод, который изначально разрабатывался для разложения сигнала с аддитивными компонентами — я говорю об ICA. При этом принимается гипотеза, что эти компоненты имеют не нормальное распределение, и их источники независимы. Простейший пример — вечеринка, где множество голосов смешиваются, и стоит задача выделить каждый звуковой сигнал от каждого источника. Для поиска независимых компонент обычно используют два подхода: 1) с минимизацией взаимной информации на основе дивергенции Кульбака-Лейблера; 2)с максимизацией «негауссовости» (тут используются такие меры как коэффициент эксцесса и негэнтропия).
На картинке ниже — простой пример, где смешиваются две синусоиды, потом они же с помощью ICA и выделяются.
x <- seq(0, 2*pi, length.out=5000)
y1 <- sin(x)
y2 <- sin(10*x+pi)
S <- cbind(y1, y2)
A <- matrix(c(1/3, 1/2, 2, 1/4), 2, 2)
y <- S %*% A
library(fastICA)
IC <- fastICA(y, 2)
par(mfcol = c(2, 3))
plot(x, y1, type="l", col="blue", pch=19, cex=0.1, xlab="", ylab="", main="Исходные сигналы")
plot(x, y2, type="l", col="green", pch=19, cex=0.1, xlab = "", ylab = "")
plot(x, y[,1], type="l", col="red", pch=19, cex=0.5, xlab = "", ylab = "", main="Смешанные сигналы")
plot(x, y[,2], type="l", col="red", pch=19, cex=0.5, xlab = "", ylab = "")
plot(x, IC$S[,1], type="l", col="blue", pch=19, cex=0.5, xlab = "", ylab = "", main="ICA")
plot(x, IC$S[,2], type="l", col="green", pch=19, cex=0.5, xlab = "", ylab = "")
Какое отношение имеет ICA к задаче уменьшения размерности данных? Попробуем представить данные — вне зависимости от их природы — как смесь компонент, тогда можно будет разделить эту смесь на то количество «сигналов», которое нам подходит. Особого критерия, как в случае с PCA, по выбору количества компонент нет — оно подбирается экспериментально.
Последний подопытный в этом обзоре — автоэнкодеры, которые представляют собой особый класс нейронных сетей, настроенных таким образом, чтобы отклик на выходе автокодировщика был максимально близок к входному сигналу. Со всей мощью и гибкостью нейронных сетей мы одновременно получаем и массу проблем, связанных с поиском оптимальных параметров: количества скрытых слоев и нейронов в них, функции активации (sigmoid, tanh, ReLu,), алгоритма обучения и его параметров, способов регуляризации (L1, L2, dropout). Если обучать автоэнкодер на зашумленных данных с тем, чтобы сеть восстанавливала их, то получается denoising autoencoder. Предварительно настроенные автокодировщики также можно «стыковать» в виде каскадов для предобучения глубоких сетей без учителя.
В самом простом представлении автоэнкодер можно смоделировать как многослойный перцептрон, в котором количество нейронов в выходном слое равно количеству входов. Из рисунка ниже понятно, что, выбирая промежуточный скрытый слой малой размерности, мы тем самым «сжимаем» исходные данные.
Собственно, в пакете h2o, который я упоминал выше, такой автоассоциатор присутствует, поэтому будем использовать его. Сначала я хотел показать пример с жестами, но быстро убедился, что несколькими предложениями тут не отделаешься, поэтому далее будут картинки с набившими всем оскомину рукописными цифрами из этого соревнования.
Данные представлены в виде .csv файлов (train.csv и test.csv), их довольно много, поэтому в дальнейшем для упрощения я буду работать с 10% данных из train.csv; колонка с метками (labels) будет использоваться только для целей визуализации. Но прежде чем выясним, что можно сделать с помощью автоэнкодера, посмотрим, что дают нам первые три компоненты при разложении PCA, ICA, NMF:
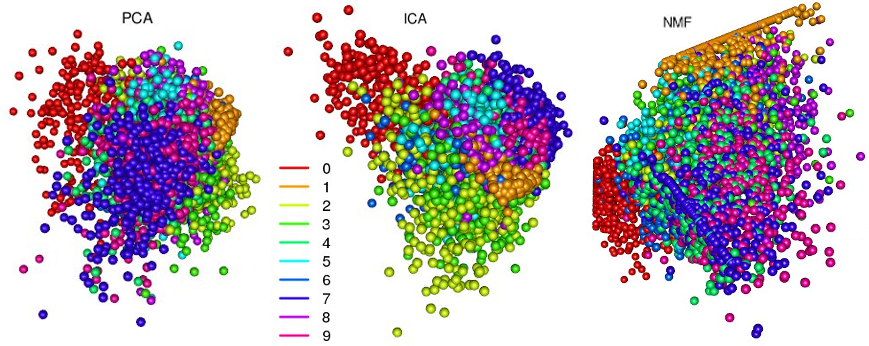
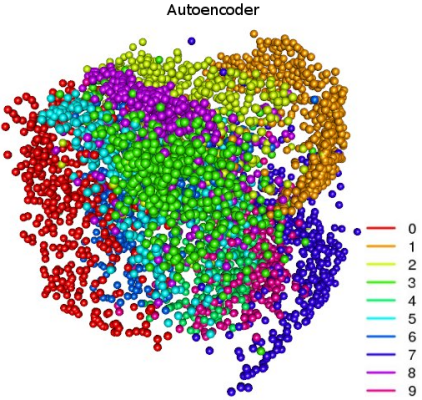
Все три метода неплохо справились с задачей кластеризации — на изображении более-менее отчетливо видны группы, плавно переходящие друг в друга. Вот эти переходы — пограничные случаи, когда цифры особенно сложны для распознавания. На рисунке с кластерами PCA очень хорошо заметно, как метод главных компонент решает важную задачу — декоррелирует переменные: кластеры »0» и »1» максимально разнесены в пространстве. «Необычность» рисунка с NMF связана как раз с тем, что метод работает только с неотрицательными матрицами. А вот такое разделение множеств можно получить с помощью автоэнкодера:
train <- read.csv("train.csv")
label <- data$label
train$label <- NULL
train <- train / max(train)
# Подготовка выборки для обучения
library(caret)
tri <- createDataPartition(label, p=0.1)$Resample1
train <- train[tri, ]
label <- label[tri]
# Запуска кластера h2o
library(h2o)
h2o.init(nthreads=4, max_mem_size='14G')
train.h2o <- as.h2o(train)
# Обучение автоэнкодера и выделение фич
m.deep <- h2o.deeplearning(x=1:ncol(train.h2o),
training_frame=train.h2o,
activation="Tanh",
hidden=c(150, 25, 3, 25, 150),
epochs=600,
export_weights_and_biases=T,
ignore_const_cols=F,
autoencoder=T)
deep.fea <- as.data.frame(h2o.deepfeatures(m.deep, train.h2o, layer=3))
library(rgl)
palette(rainbow(length(unique(labels))))
plot3d(deep.fea[, 1], deep.fea[, 2], deep.fea[, 3], col=label+1, type="s",
size=1, box=F, axes=F, xlab="", ylab="", zlab="", main="AEC")
Тут кластеры более четко определены и разнесены в пространстве. У сети довольно простая архитектура с 5 скрытыми слоями и небольшим количеством нейронов; в третьем скрытом слое всего 3 нейрона, и фичи оттуда как раз и изображены выше. Еще немного занимательных картинок:
W <- as.data.frame(h2o.weights(m.deep, 1))
pdf("fea.pdf")
for (i in 1:(nrow(W))){
x <- matrix(as.numeric(W[i, ]), ncol=sqrt(ncol(W)))
image(x, axes=F, col=gray(0:255 / 255))
}
dev.off()
На самом деле, это всего лишь изображения весов нейронов: каждая картинка ассоциируется с отдельным нейроном и представляет фильтр, который выделяет специфичную для данного нейрона информацию. Вот для сравнения весы выходного слоя:
Вышеозначенный автоэнкодер несложно превратить в denoising autoencoder. Так как такому автокодировщику на вход надо подавать искаженные образы, перед первым скрытым слоем достаточно разместить dropout слой. Благодаря ему с некоторой вероятностью нейроны будут находиться в «выключенном» состоянии, что а) будет вносить искажения в обрабатываемый образ; б) будет служить своеобразной регуляризацией при обучении.
Еще одно интересное применение автоэнкодера — определение аномалий в данных по ошибке реконструкции образов. В целом, если подавать на вход автоэнкодера данные не из обучающей выборки, то, понятно, ошибка реконструкции каждого образа из новой выборки будет выше таковой из тренировочной выборки, но более-менее одного порядка. При наличии аномалий эта ошибка будет в десятки, а то и сотни раз больше.
Заключение
Безусловно, было бы неверно написать, что какой-то метод сжатия лучше или хуже других: каждый имеет свою специфику и область применения; многое зависит от природы самих данных. Не последнюю роль тут играет и скорость работы алгоритма. Из рассмотренных выше самым быстрым оказался SVD/PCA, потом по порядку идут ICA, NMF, и завершает ряд автоэнкодер. С автоассоциатором работать особенно сложно — не в последнюю очередь благодаря нетривиальности в подборе параметров.
