Как робот 3D сканирует
В мире существует множество технологий 3D сканирования. На базе каждой из них созданы десятки моделей сканеров. Какие-то сканеры умеют сканировать только мелкие объекты, какие-то предназначены для сканирования людей. Другие могут отсканировать дом или комнату. Одно только перечисление всевозможных вариаций сканеров заняло бы целую статью.
В этой статье я расскажу об одном из перспективных направлений сканирования — о том как делаются роботизированные 3D сканеры.
Зачем это нужно?
Сканирование трёхмерного объекта это не мгновенный процесс. Он требует от человека производить постоянный анализ текущей ситуации и, в зависимости от результатов, корректировку своих действий. Сканирование больших объектов может занять некоторый период времени.
Примеры можно посмотреть тут и тут.
Если нужно сканировать много объектов (например, для решения задачи контроля качества или для оцифровки ассортимента магазина), то лучше всего конечно же избавить себя от рутины и использовать робота. Может это и не сильно ускоряет процесс, зато делает результат стабильным, повторяемым и избавляет оператора от физического труда.
(На самом деле главный аргумент — это конечно же: потому что это круто! Человекоподобные роботы и все дела!)
Основное отличие и сложность процесса
Когда сканирует человек, он видит всё: что отсканировано плохо, что — не до конца, где в сканируемом объекте дырка. Глаза — это независимый сканер, который позволяет проверить качество поступающих данных и сказать «АГА! Вот тут ты не доглядел!». Но когда сканирует робот, то такие решения должен принимать он сам. И единственная информация для принятия таких решений — данные, полученные со сканера. А данные зачастую выглядят так: 

Тут приведён результат того, что будет, если поводить сканером секунд 15–20 около объекта.
Все сканеры при сканировании выдают либо облако точек, либо облако полигонов, либо карту глубин. Любой вид информации может содержать дырки. Дырки могут появляться по целому ряду причин:
- В объекте и правда может быть дырка
- В объекте есть углубление. Иногда сканер просто не может заглянуть внутрь: база между «глазами» слишком большая
- Если сканирование происходит путём излучения на некоторой частоте, а внутри области есть материал, поглощающий излучение на данной частоте, (или зеркальное отражение) — то опять будет дырка
- Если сканирование происходит пассивным сканером с двумя камерами, а область монотонная, то… ну вы уже поняли
- Большой угол у плоскости сканирования к сканеру тоже может вызвать прореху
- Дырка будет, если отсканировать со стороны «дырки» нельзя. Например, основание статуи или тыльная сторона статуи, стоящей близко к стене (бывало и такое)
- Уверен, можно придумать еще случаи
Но робот-сканер не знает причин. Он не знает, закончился ли объект, или он бликует. Робот не имеет независимых средств контроля. Он познаёт окружающий мир только через сканер.
Как бороться?
Первый и самый простой способ — набрать избыточное количество данных или попросту постараться отсканировать объект со всех возможных сторон. Например, вот так:
У такого подхода есть ряд минусов:
- Время сканирования довольно велико. Приходится долго крутить объект.
- В случае простых форм (а-ля банка из под пива) все будет хорошо, но как только мы попробуем отсканировать что-то довольно сложное с больших количеством «поднутрений», окажется, что остается много не отсканированных зон
- Не факт, что все положения будут пройдены. Например, чтобы увидеть какую-то точку внутри объекта, нужно посмотреть строго с одной стороны с точностью до пары градусов, а пройти все 2πR2≈41253 квадратных градусов — нереально (пусть даже с отрезанной нижней полуплоскостью ≈20к)

(кадр из видео выше, видны ошибки внутри втулки)
Второй подход — заранее просчитанная траектория. Разумеется, это можно сделать только в ограниченном количестве сценариев, когда форма объекта примерно известна. Например, на производстве для решения задачи контроля качества изготовленного изделия.
Третий, самый разумный и интересный способ — в зависимости от наблюдаемого объекта выбрать минимальное количество видов и оптимальную траекторию движения руки со сканером таким образом, чтобы добиться максимального покрытия объекта.
По получаемым данным строится замкнутая поверхность. После чего итеративно наблюдаются области по которым самая низкая достоверность (поверхность есть, но точек, её подтверждающих — нет). Наблюдаем область — > пересчитываем модель — >наблюдаем область. В итоге получается целая серия последовательных сканов в результате которой робот «познаёт» объект
Дело осталось за малым: взять математику, которая позволит строить поверхность. Добавить модуль оценки достоверности построенной поверхности. Запустить в цикле.
Poisson Reconstruction
Наиболее интересная и красивая математика, решающая проблемму построения поверхности по неполным данным — «восстановление Пуассона». Основное предположение — мы рассматриваем один объект. Тогда мы можем вообразить себе «скрытую» функцию f (p) от позиции в пространстве. Положительное значение — вне объекта, отрицательное — внутри. На искомой поверхности объекта функция будет нулевой.
Понятно, что градиент f (p) на поверхности — это и есть вектор нормали к искомой поверхности объекта.
При обработке первичных данных от сканера мы уже оцениваем нормали к сканируемой поверхности. Тогда входными данными для поиска функции f (p) будет набор точек в пространстве и нормали к поверхности объекта в этих точках: (p, n)i Обычно при сканировании более менее сложного объекта таких точек сотни тысяч.
Смысл этой функции f (p) и нормалей проще всего понять в 2D. Слева — нормали к 2D объекту, справа –значение функции f (показано третьей координатой), синий цвет — вне объекта, оранжевый — внутри.
Точки (p, n)i лежат на поверхности. В идеале: 
где перевернутый треугольник — оператор Набла (вектор градиента).
Естественно, нормали в точках и сами позиции точек содержат ошибки измерения, поэтому не найдется такой функции f, да и не стоит ее искать. В этой ситуации вводят поле нормалей v (x) и требуют минимума: 
Решается эта минимизационная задача как раз с помощью уравнения Пуассона: 
Кому интересно более подробно почитать про вывод и математику: статья автора придумавшего метод.
А решив это уравнение (есть много способов решить задачу, но придется, конечно, перейти к разностной задаче, а затем и к огромному линейному уравнению), нужно будет найти изоповерхность с нулевым значением f, и с помощью алгоритма марширующих кубов построить полигональную модель.
Тут, кстати, появляется сразу несколько проблем, которые приходится преодолевать:
- Поле v (x) — поле нормалей, на самом деле несколько не дифференцируется, а, значит, придется их как-то «размазывать» по пространству. Иными словами — фантазировать.
- Решение задачи Пуассона с точностью до константы. А нам надо найти поверхность объекта, значит придется решать еще одну оптимизационную задачу, чтобы минимизировать значения функции f во всех точках pi.
Но со всех остальных сторон этот математический подход хорош и надежно применим в реальности (хоть и не быстрый процесс вычисления).
Единственное, т.к. плотность точек pi в пространстве очень переменна, то целесообразно разбить весь объем с помощью октодерева и решать итоговое разностное уравнение с учетом разбиения на кубики разного размера.
Можно, либо задать самый мелкий уровень разбиения, либо дробить пространство до тех пор, пока в каждой клетке останется не больше чем одна точка с нормалью. В итоге, количество кубиков будет сопоставимо с количеством точек, полученных при сканировании.
Smooth Signed Distance Surface Reconstruction (почти Poisson Reconstruction)
Есть еще один подход, предложенный F. Calakli and G. Taubin в 2011 г., который дает такой же качественный результат, а при определенных условиях даже лучше, как и метод с решением уравнения Пуассона, но несколько доступней для понимания и программирования. В википедии же эти два метода просто путают.
Аналогично ищем функцию f (p), которая отрицательна внутри объекта, а положительна вне его. Точно также градиент f (p) хотим приблизить к нормалям в заданных позициях, которые мы получили при сканировании. Но будем искать минимум: 
Выглядит довольно громоздко, но на самом деле мы лишь просим, чтобы функция в точках Pi была бы поменьше (первый член), чтобы градиент ее был поближе к нормалям в тех же точках (второй член), и чтобы во всем объеме у нее вторые производные были поменьше, точнее — Гессиан функции (третий член). Требование на вторые производные, довольно важное, т.к. очень хочется, чтобы уйдя за границы объекта, функция не начала осциллировать, и не получилось таких кошмарных картинок: 
Т.е. все минимизировали, но уйдя подальше от точек, которые мы промерили сканером, функция f (p) не повела себя произвольно.
И, заметьте, что каждый член — квадрат. Это не просто так, т.к. именно для квадратичных форм несложно аналитически получить экстремум (для форм A*A-2*b*A+c локальный минимум в точке A=b). Только запишем все в разностном виде, т.е. заменим частные производные на разности на границах маленьких кубиков, а потом в матричном, чтобы воспользоваться фокусом с минимумом квадратной формы. И в итоге получим линейную систему уравнений, неизвестные в котором — значения функции f (p) внутри кубиков. А кубики, также как и в описанном выше методе реконструкции, стоит брать неравномерно, а строить октодерево. Кому интересно подробный вывод, текст статьи.
Работает по скорости примерно также, как и метод, основанный на уравнении Пуассона. Есть одно маленькое преимущество в том, что не нужно «размазывать» нормали по пространству, чтобы иметь возможность получить дивергенцию от векторного поля нормалей, теряя при этом точность и излишне сглаживая объект. С другой стороны, если сканер довольно грубо оценивает нормали, то это преимущество может стать недостатком метода.
Мера качества
Сам по себе алгоритм Пуассона не говорит нам, что видно, а что нет. Нужно придумать некоторую меру качества для оценки достоверности результата. Самая простая мера — пройти вдоль поверхности небольшими кубиками и посмотреть как много попало точек в каждый из них: 
Чем больше точек — тем больше достоверность, тем более красного цвета. Такая мера качества будет весьма репрезентативной. Действительно, мы не можем доверять областям, где ничего не видели. А уж если видели, то, наверное, там действительно что-то есть.
Выбор дальнейшего направления сканирования
Теперь вроде всё понятно. Нам нужно выбрать такие точки дальнейшего сканирования, с которых сделать следующую серию кадров, которую замерджить в основную модель.
Для этого мы разметим окружающее пространство. Каждую его точку проверим, определив сколько недостоверных точек фигуры мы увидим из неё. Чем больше таких точек — тем выгоднее смотреть.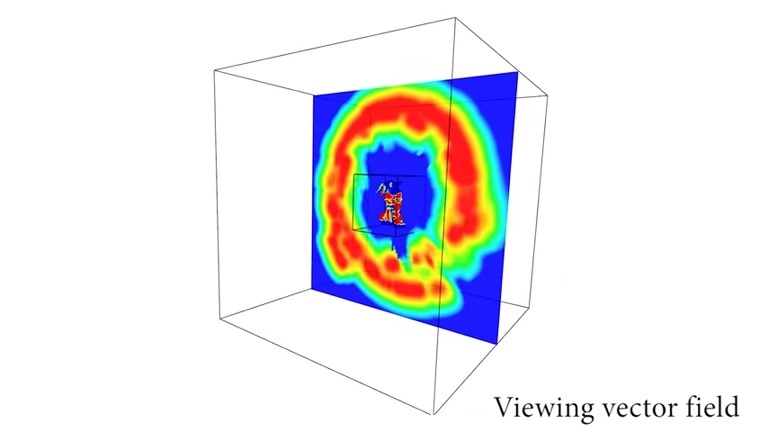
Остаётся найти локальные максимумы и запускать наблюдения: 
Потом опять выполняется Пуассон, потом опять выполняется дополнительное сканирование. И так по кругу, пока не появится готовая модель.
А нужен ли вообще Пуассон?
Может можно отсканировать хорошо, чтобы всё было и так? Зачем усложнять кучей математики? Вот простой пример. Три картинки. Скан был сделан сканером Artec Spider. Первый — сырая информация со сканера, по сути облако точек. Второй — алгоритм «Fusion», который просто делает усреднение и контроль положения. Третий — алгоритм Пуассона. И ведь разница на лицо! 


А вот так этот дракоша будет выглядеть целиком: 
Собираем всё воедино
В итоге, алгоритм сканирования поверхности роботом выглядит следующим образом:
- Делаем первичный скан
- Строим по имеющейся информации аппроксимирующую поверхность
- Строим меру качества данной поверхности
- Выбираем точки для дальнейшего сканирования
- Если у точек большая важность — сделать скан и перейти к п.2
- Если при сканировании информации почти не добавится — выдать пользователю итоговый скан
Более подробно про такую схему сканирования можно почитать, например, здесь.
Или посмотреть как всё это дело работает:
P.S. Робот в видео крутит головой просто так, к сканированию это не имеет отношения
P.S. S. Спасибо Vasyutka за помощь в написании статьи и команде Артека за многочисленные правки и доведение до ума!
