Как работают Векторные базы данных и Поиск похожих текстов в них
Если вы когда-нибудь использовали в работе retrieval augmentation generation (RAG), то наверняка знаете, что векторная база данных внутри решения находит похожие куски текста, которые вы туда загрузили ранее с помощью ретривера (эмбеддера). Если вы никогда не лезли туда под капот, но были бы не прочь понять, каким образом находятся именно нужные куски текста, я постараюсь верхнеуровнево показать вам, как устроен поиск похожих документов в векторной базе данных.
Данная статья будет полезна тем, кто только погружается в NLP, и, в частности, в RAG.
В данной статье я собираюсь:
Осветить, как конвертируется текст в векторы скрытого пространства (кратко).
Рассказать какие есть основные меры для поиска похожих векторов и почему knn — это очень долго.
Подробно разобрать один из алгоритмов приближенного поиска ближайшего соседа -Navigable Small World и погрузить в метод Hierarchical Navigable Small World.
Автоэнкодер и скрытое пространство
Для начала, кратко вспомним о том, что из себя представляет автоэнкодер.

Автоэнкодер старается наиболее точно восстановить подаваемые на вход данные.
Автоэнкодер — нейронная сеть, которая сначала сжимает входные данные в скрытое пространство (секция энкодера), после чего восстанавливает их в неизменном виде (секция декодера). По архитектуре похож на персептрон. Цель — получить на выходном слое данные, наиболее близкие к входному.
В процессе обучения автоэнкодера вначале мы будем получать на выходе не очень похожие на вход данные:

Картинка на выходе не похожа не картинку на входе
Однако после достаточно хорошего обучения мы уже сможем восстанавливать похожие на вход данные:

Хорошо обученный автоэнкодер достаточно точно восстанавливает входное изображение
Причем, не так уж и важно, что это за данные, главное — чтобы они были не случайными, и нейросеть могла из обработать. Именно к таким данным и относится предварительно токенизированный текст.
Как и в Word2Vec, в скрытом представлении хорошего автоэнкодера учитывается семантика кодируемого текста. Таким образом, похожие по смыслу тексты будут расположены достаточно близко в эмбеддинге, и можно находить по эмбеддингу запроса (querry) те тексты и документы, которые близки ему по смыслу.
Что значит расположены близко?
Меры расстояния между векторами
На самом деле, существует много способов оценить расстояние между двумя векторами. В этой статье я кратко освещу лишь 4 из них:
Евклидово расстояние (L2).
Манхэттенское расстояние (L1).
Скалярное произведение.
Косинусное расстояние.
Евклидово расстояние (L2).
Евклидово расстояние — это длина кратчайшего пути между двумя точками или векторами.

Евклидово расстояние
Манхэттенское расстояние (L1)
Манхэттенское расстояние, или расстояние городских кварталов равно сумме модулей разностей их координат.
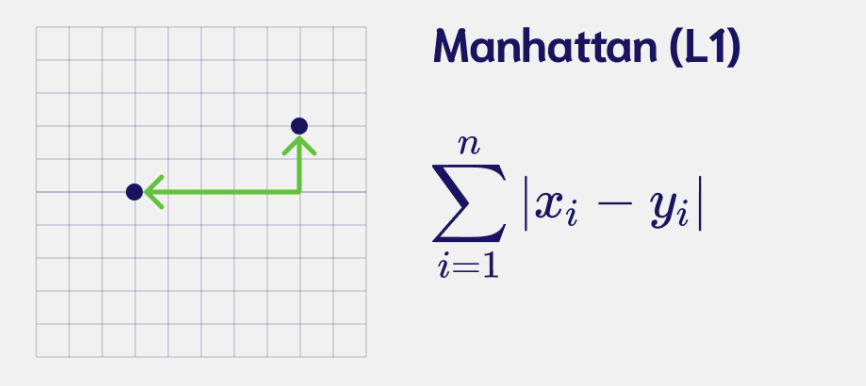
Манхэттенское расстояние
Скалярное произведение
Скалярное произведение равно сумме произведений соответствующих координат векторов.

Скалярное произведение
Косинусное расстояние
Косинусное расстояние представляет собой разницу в направлении векторов.

Косинусное расстояние
В NLP чаще используются скалярное произведение и косинусное расстояние.
Поиск ближайшего вектора методом ближайших соседей
Хорошо, вот мы выбрали меру расстояния по которому будем находить ближайшего соседа (точнее, ближайших k соседей). Теперь остро встает вопрос, как это сделать.
Первым, и не самым плохим вариантом, будет, рассчитать расстояние от заэмбеженного вектора запроса до эмбеддингов всех текстов и документов, хранящихся в нашей базе. Отсортировать эти расстояния по возрастанию и взять k ближайших соседей.
Давайте попробуем погенерировать демонстрационные данные для оценки скорости выполнения запроса.
import numpy as np
import time
np.random.seed(42)
n_docs = [1_000, 10_000, 100_000, 500_000]
n_dims = 768
for n in n_docs:
# Генерируем векторы для оценки времени выполнения запроса
embeddings = np.random.randn(n, n_dims)
# Генерируем сам запрос
query = np.random.randn(768)
# Замеряем время на ранжирование ближайших соседей
t0 = time.time()
similarities = embeddings.dot(query)
sorted_ix = np.argsort(-similarities)
t1 = time.time()
total = t1-t0
print(f"Время выполнения 1 поиска среди {n} документов в базе: {np.round(total,3)} секунд")Время выполнения 1 поиска среди 1000 документов в базе: 0.001 секунд
Время выполнения 1 поиска среди 10000 документов в базе: 0.001 секунд
Время выполнения 1 поиска среди 100000 документов в базе: 0.017 секунд
Время выполнения 1 поиска среди 500000 документов в базе: 0.085 секунд
Рассчет 1000 запросов
print (f"На выполнение 1,000 запросов потребуется: {total * 1_000/60 : .2f} минут")На выполнение 1,000 запросов потребуется: 10.61 минут
Как можно увидеть, даже при небольшом (500 000) количестве документов в нашей базе, время обработки тысячи запросов выливается в копеечку, а учитывая, что сложность алгоритма поиска — O (n), при увеличении нашей базы знаний, время обработки запросов будет расти линейно.
Navigable Small World. Построение графа
Navigable Small World — метод основанный на графе, позволяющий эффективно искать k почти что ближайших соседей на небольших множествах вершин. Почему «почти что» — Разберем в процессе разбора метода поиска по графу.
Начнем с построения вершин, среди которых нужно найти наиболее близкую к запросу вершину (вершины — это эмбэддинги текстов, документов, или других документов, которые мы перевели в скрытое пространство заданной длины). В данном случае я буду использовать Евклидово расстояние, чтобы было нагляднее на 2D графике.
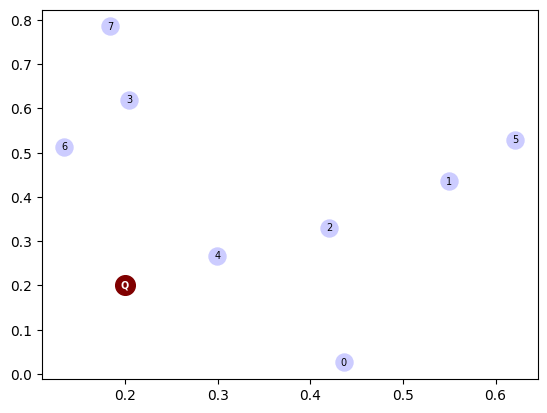
Запрос от пользователя (Q) и набор документов, среди которых производится поиск.
Построение графа мы начинаем с любой вершины. Далее мы добавляем по одной вершине, также случайной. Каждую новую вершину мы соединяем с не более, чем двумя ближайшими вершинами, которые уже включены в граф.

Начинаем строить граф с точки 1 и, соответственно, включаем ее в граф.

У точки 5 нет вариантов, кроме как быть соединенной с точкой 1

У точки 7 также нет альтернативных кандидатов, кроме точек 1 и 5

А вот точка 3 уже выбирает, между 1 и 5, и 1 ближе, значит строим ребро (1,3)

Повторяем поиск ближайших двух вершин в графе для всех оставшихся свободный вершин

Повторяем поиск ближайших двух вершин в графе для всех оставшихся свободный вершин

Повторяем поиск ближайших двух вершин в графе для всех оставшихся свободный вершин

Повторяем поиск ближайших двух вершин в графе для всех оставшихся свободный вершин
Navigable Small World. Поиск по графу.
Конечно, построить первоначальный граф — требует вычислений: ведь нужно считать расстояние от каждой новой вершины до всех остальных. Но нам важна скорость поиска, чтобы быстро обрабатывать запросы клиентов. И с этим данный метод справляется достаточно не плохо (но можно и лучше — об этом чуть далее).
Поиск мы также начинаем со случайной вершины уже построенного графа и оцениваем расстояние от каждой из вершин, соединенных с выбранной до нашего запроса. На графике будет нагляднее.

Выбрали вершину 1
Например, мы выбрали вершину 1. У нее ребра соединены с 5ю другими вершинами. Измеряем расстояние выбранным способом от каждой из этих вершин до нашего запроса. Также не забываем про саму вершину 1 (ведь мы же могли изначально случайно попасть в самую ближайшую вершину). Ближе всего к запросу располагается вершина 2. Переходим в нее и повторяем процедуру до тех пор, пока не останется кандидатов, которые расположены ближе к запросу.

На предыдущем шаге была выбрана точка 2. У нее из кандидатов поиска — вершины 4 и 0

На вершине 4 поиск завершается.
Так почему же этот метод позволяет найти «почти что» самую ближайшую вершину?
Потому что мы не всегда будем приходить к наиболее близкой к запросу вершине. Давайте представим, что мы начали поиск с вершины 3.

Начали поиск с другой точки.
У вершины 3 есть три кандидата, не считая ее саму: 1, 7 и 6. Замерив расстояние до запроса от каждой из них, мы выберем точку 6. И на этом поиск завершится. Ведь из точки 6 нет ребер, соединяющих ее с более близкой к запросу вершине.

В вершине 6 поиск завершается.
Но тем не менее мы получили достаточно неплохой результат, сделав при этом минимальное количество расчетов. Но что, если точек ОЧЕНЬ много? Тут нам поможет такая структура данных, как Hierarchical Navigable Small World (Иерархический маленький мир).
Hierarchical Navigable Small World
Данная структура состоит из нескольких графов Navigable Small World, описанных выше.
Причем количество входящих точек в соответствующий граф уменьшается тем сильнее, чем выше данный граф располагается в данной структуре (нумерация начинается снизу).
Для лучшего понимания представлю очень хороший график, который я нашел на иностранном ресурсе.

Из-за того, что на верхнем слое мало точек, мы быстро покрываем расстояние до цели.
На верхнем слое в графе представлены лишь три вершины. Это позволяет нам с наименьшим количеством переходов пройти наибольший путь до цели (наш запрос).
На самом нижнем слое все вершины должны быть соединены в граф. Если провести аналогию с реальным миром, мы можем представить, что нам из Москвы нужно добраться в маленькую деревню в Сибири. Мы садимся на скорый поезд, который пропускает много остановок (верхний слой), в крупном городе сходим и пересаживаемся на обычный поезд. Возможно даже, что нам придется вернуться чуть назад. Доезжаем до маленького города, там пересаживаемся на электричку, и, наконец, на маршрутке или на автобусе добираемся до пункта назначения (нижний слой). Конечно, мы могли пройти весь маршрут на разных автобусах, но сколько времени это бы у нас заняло?
Hierarchical Navigable Small World же позволяет нам доходить до пути за наименьшее количество шагов. Сложность поиска в этой структуре занимает O (log (n)), в отличии от O (n) при использовании knn.
Заключение
Таким образом, мы повторили, как делаются эмбеддинги документов, загружаемые в векторные базы данных, какие меры расстояния используются для оценки схожести этих документов, а также на примере одной структуры данных поняли, как осуществляется поиск похожих на наш запрос документов. Это не единственный способ поиска похожих документов, но, надеюсь, что понимание того, как он устроен, поможет вам в работе.
Спасибо за внимание.
