Как я гонял Балду-2, или в поисках оптимального алгоритма
Балдология, как оказалось (вы ведь слышали о существовании такой науки, правда?), имеет на Хабре отражение в виде нескольких статей, вот они: «Алгоритм быстрого поиска слов в игре балда«Алгоритм и тактика поиска слов в игре Балда«Как я гонял Балду на Visual Basic for Applications для MS Access»
Эта статья — продолжение моей предыдущей, последней в списке. Отправными точками для написания были присланные мне в комментариях ссылки на способ хранения словаря в виде дерева (статья в Википедии с описанием алгоритма Trie), а также упоминание коллеги chibiryaev о его собственной реализации поиска, которая тратит на нахождение слова в словаре из 110 000 элементов всего 16 миллисекунд!
Собственно, задача №1 — увеличение скорости поиска слов в текстовом массиве.Начнем с реализации алгоритма Trie. Для этого нам необходимо поместить весь словарь существительных (43 303 слова) в структуру связанного дерева. Visual Basic не поддерживает переменных-ссылок, подобно C++ или C# (не говоря уже о Pascal), но в этом качестве вполне подойдут индексы массива.Каждый элемент массива должен хранить следующую информацию:
— Букву, — Индекс элемента массива, с которого начинаются буквы, следующие за данной буквой в реально существующих словах, — Количество элементов в этом списке букв-продолжений, — Признак того, получим ли мы законченное словарное слово, если остановимся на текущей букве.
На картинке это выглядит так

Массив должен содержать три типа данных — букву, логическое значение и числовое значение. Попытка сделать его универсальным для Visual Basic типом Variant, когда элемент массива может быть любым — хоть объектом, ни к чему хорошему не привела — в итоге было задекларировано 4 массива одинаковой длины, каждый нужного типа, что прибавило к скорости работы существенные 25%.Наполнение подобного массива происходит, понятно, с помощью рекурсивной функции. Для нее, что интересно, также необходим механизм поиска в массиве строк))) Выход из этого замкнутого круга проливает свет на одну интереснейшую программистскую технологию, называемую «раскруткой». Суть ее в следующем.
Такую сложную программу, как оптимизирующий компилятор с языка С++, например, лучше всего писать… на языке С++. Ну не на ассемблере же! Где взять тогда такой компилятор, если мы только хотим его создать? Ответ таков — нужно взять любой, самый примитивный, неоптимизирующий, написанный чуть не на коленке, лишь бы работал без ошибок. Затем мы прогоняем через него наш исходный текст, и получаем на выходе программу-компилятор — медленную, как Windows NT 3.51, но уже умеющую оптимизировать и все прочее, что мы в нее заложили. А вот скормив ей еще раз наш исходный код, мы обретем уже желаемое во всей своей красе. Другой способ — написать полноценный компилятор на неком простом подмножестве С, для которого сделать опять-таки примитивнейший генератор кода, а потом как выше. (Статья в Википедии на эту тему)
Поэтому для создания и наполнения дерева-словаря я использовал алгоритм поиска через 2-буквенный индекс из предыдущей версии своей программы.
Мне захотелось сравнить результат с предыдущим — когда поиск осуществлялся с помощью 2-буквенного индекса. Оказалось, что выигрыш совсем невелик, процентов 7 с небольшим. Кардинальное отличие лишь в способе хранения исходного словаря.Но у меня получилось ускорить этот алгоритм еще в три с лишним раза.
Я давно вывел для себя, что в программировании существует, по аналогии с физикой, нечто вроде «правила рычага». В физике это звучит так «Выигрываем в силе — проигрываем в расстоянии». В программировании — «Выигрываем в быстродействии, проигрываем в объеме необходимой памяти».
На примере: есть 2 способа ввести в компьютер операцию умножения. Либо реализовать ее в виде алгоритма, либо составить массив всех возможных пар чисел с их произведениями, и при запросе выбирать уже готовый результат прямо из таблицы. Между прочим, в школе учат умножать с помощью обоих этих методов. Сначала мы запоминаем таблицу умножения для чисел от 1 до 9, а потом уже используем запомненные результаты для умножения любых чисел с помощью алгоритма «в столбик».
Я отвлекаюсь здесь от физической возможности запомнить все пары чисел с их произведениями. К тому же, существуют промежуточные варианты — что-то предрассчитать и сохранить, и использовать затем для ускорения выполнения алгоритма. Самый яркий пример такого рода — знаменитая ошибка в процессоре Intel Pentium Для реализации быстрого алгоритма деления использовалась таблица поиска длиной 1024 байта, которую нерадивый сотрудник заполнил неверно. Ошибка стоила корпорации почти полмиллиарда долларов — Intel-у пришлось заменить все процессоры с ошибкой, и это в ценах 1994 года!
Если попытаться применить теперь правило рычага (имени меня)), то где узкое место поиска в дереве? При нахождении нужной нам буквы-продолжения среди элементов по ссылке от буквы текущей. Чтобы избежать этого поиска, давайте хранить в массиве не только те буквы, которые присутствуют в реальных словах, а все 32, помечая просто, что некоторые из них в словах не встречаются. Это позволит нам сразу переходить на нужный элемент массива, попросту рассчитав его индекс из буквы. Эту структуру естественно назвать «разреженным деревом». Размер массива при этом, надо сказать, вырастет весьма существенно — если обычное дерево занимало 169 693 элемента, то разреженное — уже 5 430 177 (правда, в каждом элементе соответствующего разреженного массива достаточно хранить 2 величины, а не 4 — не нужна сама буква, она определяется местом в алфавите, и также количество элементов по ссылке всегда равно 32).

Вот соответствующая картинка — обратите внимание, насколько увеличился номер индекса для тех же слов (столбцы (X) для пояснения, их нет в массиве — не нужны):

Ну и самый экстремальный случай, когда ответ о принадлежности слова словарю дается в одну команду. Пусть все слова некоторой длины хранятся в логическом массиве соответствующей размерности, как на картинке для 2-буквенных слов.
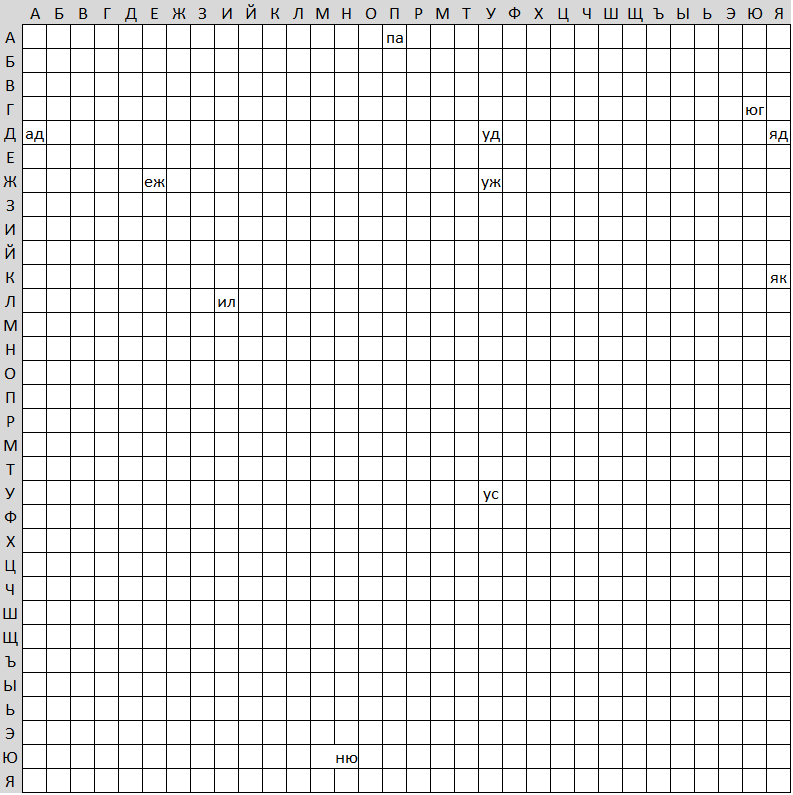
Здесь нам нужно просто смотреть значение элемента массива
СЛОВАРЬ ('Б', 'А', 'Л', 'Д', 'А') = TRUEСЛОВАРЬ ('Х', 'А', 'Б', 'Р') = FALSE
(последнее возмутительно!)
Расход памяти при этом (чудовищный) посчитаем чуть ниже.Итак, сравнение 4 алгоритмов на словах разной длины. Генерировалось сначала миллион, а потом сто миллионов случайных слов, длиной от 4-х до 24 –х букв, после чего оценивалось время поиска.
1. Поиск по 2-буквенному индексу.2. Поиск по обычному дереву3. Поиск по разреженному дереву4. Прямой поиск в массиве (ввиду ограничений на размер массивов возможен только для слов длиной не более 6 букв, да и то — 6-буквенные с оговорками). Зато как быстро!
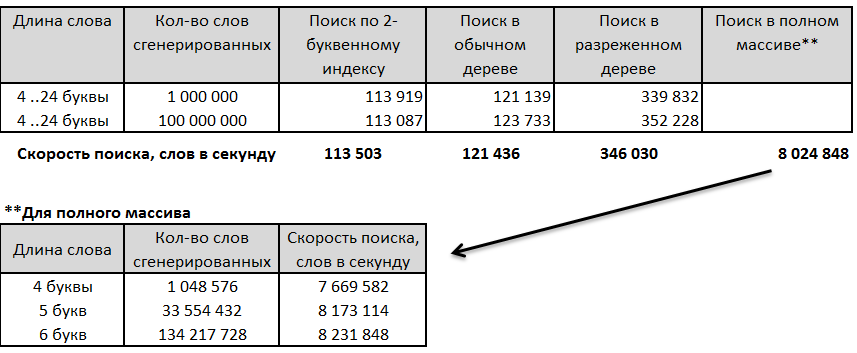
(Нужно упомянуть компьютер, на котором я считал — это Intel Core i3 -2125 на частоте 3.3GHz, 4GB оперативки. Процессор 4-ядерный, но это, я подозреваю, неважно, так как задача нераспараллеленная, разве что сама операционка и прочие процессы сидят на других ядрах и не мешают нашему счету.)
Небольшой оффтоп — список самых длинных существительных
22 ВОЗДУХОНЕПРОНИЦАЕМОСТЬ22 НЕДИСЦИПЛИНИРОВАННОСТЬ22 НЕПРЕДУСМОТРИТЕЛЬНОСТЬ22 НЕУДОВЛЕТВОРИТЕЛЬНОСТЬ22 ОБЩЕРАСПРОСТРАНЕННОСТЬ22 САМОУСОВЕРШЕНСТВОВАНИЕ23 ПЕРЕОСВИДЕТЕЛЬСТВОВАНИЕ24 ВЫСОКОПРЕВОСХОДИТЕЛЬСТВО24 ЧЕЛОВЕКОНЕНАВИСТНИЧЕСТВО
Не удивительно, что самые длинные слова в основном составные. Кстати, есть весьма изящная теория, что количество слов в языке, вообще говоря, бесконечно. Поскольку есть немаленький список исходных корней и правила образования из них новых слов (вспомните хотя бы производные того, что англичане называют f-word). Эта теория, конечно же, более понятна и мила программистам с их знакомством с рекурсией, чем самим филологам! Но я ее так же придерживаюсь. Одно время я даже собирал такие новообразованные слова:
— «он имел вид свежевыпоротого кота» (откуда это?)— «в Москве прошли советско-слоново-берего-костийские переговоры» (из коллекции ляпов дикторов Центрального Телевидения СССР. Упомянутая страна — Берег Слоновой Кости — сейчас называется Кот Д'Ивуар, что то же самое, только по-французски)— «лечу табакокурение» (на заборе)
Последнее словообразование меня особо позабавило. Можно, следуя этим путем, напридумывать много всяких новых слов. «Водкопитие», например. Или «девкогуляние»))
Кстати, даже будучи носителем этого самого великого и могучего русского языка, не всегда возможно понять, придуманное ли слово перед нами или нет. Например, в словаре Зализняка есть слово «самолетовождение», которое кажется мне еще более искусственным, чем отсутствующее там «табакокурение»! А «Балдология»? В общем, непаханое поле.
Интересно посмотреть на описанные алгоритмы еще вот в каком разрезе. Правило рычага в физике очень конкретно — произведение силы на расстояние, что есть физическая величина, называемая работой, неизменно. Хочешь поднять вдвое более тяжелый груз — используй рычаг в 2 раза длиннее, и обойдешься тем же усилием. Давайте попробуем посчитать, как соотносится затраченная на хранение всех этих массивов память по сравнению с выигрышем в скорости.
Тут есть некая дилемма. Ради быстродействия хранение данных в компьютере организовано в очень некомпактном виде. Процессор быстрее всего работает с двойными словами длиной 4 байта (или уже даже с четверными — в 8 байт?). Поэтому все компиляторы хранят данные очень неэкономно. Нам для хранения признака наличия слова в словаре достаточно одного бита (boolean), а в памяти это будет двойное слово. (Аттракцион невиданной щедрости! Запроси у операционной системы 1 бит памяти и получишь еще 31 совершенно бесплатно! Пользователи же привилегированных 64-битных систем получают бесплатно целых 63 бита!)
Но, наверно, для чистоты подсчета нужно брать реальное количество нужных нам битов –теоретическая эффективность алгоритма есть вещь абстрактная, что ей до конкретной реализации в процессоре той или иной архитектуры (хотя эта реализация может существенно — буквально в разы! — менять быстродействие при работе такого алгоритма).
Кстати, мы не включили в подсчет самый простой вариант — прямого перебора. Но он в разы медленнее и собьет нам всю картину, к тому же это и не алгоритм вовсе, а так, метод грубой силы

Как видим, увеличение скорости поиска дается с каждым шагом нам все большей и большей кровью памятью.
Кстати, интересно оценить качество включенного в VBA (на самом деле, в саму Windows) генератора случайных (псевдослучайных, конечно же) чисел. Когда мы генерируем некоторое достаточно большое количество строк символов, в нем обязательно должны оказаться и реальные словарные существительные (помните присказку об обезьянах, которые печатают на пишущих машинках и делают это до тех пор, пока у какой-нибудь из них не получится полное собрание сочинений Шекспира/ Льва Толстого/ Эдуарда Лимонова?)
Поскольку мы ограничились всего-то ста миллионами генерируемых слов (всего-то! Но мне хотелось опубликовать эту статью еще при жизни), то проверить качество генератора можно только на словах из максимум 6 букв, так как на слова бо́льшей длины мы просто ни разу, как оказалось, не наткнемся. Но и на этих цифрах система демонстрирует шикарное качество! Вот результат

Характернее всего — первая строка. Она показывает отличие от теоретического максимума всего в 3 сотых процента!!! То есть нагенерируй мы еще большее количество слов, точность попадания в словарь была бы еще выше.
Ну, и на сладкое. В первом же комментарии к прошлой статье коллега zorgzerg пригрозил меня убить, так как я лишал людей кайфа игры вживую, вооружая себя и других инструментом для нечестной игры (плюс, правда, поставил)))). Имею сказать следующее. Балда относится к математическим задачам, полностью просчитываемым на совершенно среднем современном компьютере. На самом деле, к таковым задачам уже можно отнести и шахматы (после победы суперкомпьютера над чемпионом мира Гарри Каспаровым), но там и система была помощнее, и команда программистов … чуть получше. Поэтому мы, человеки, должны посвящать себя гораздо более сложным и трудноформализуемым задачам, а компьютеры пусть развлекаются сами с собой -под нашим присмотром и нам на радость. Для примера: используя последний алгоритм «разреженного дерева», я заставил компьютер, играя за обе стороны, прогнать 3 264 партии (по числу 5-буквенных слов в словаре, используемых для начала игры). На каждом шагу мой железный конь выбирал самое длинное найденное слово — первое из списка, последнее из списка, случайное из списка (если таких слов было несколько). Обычная средняя игра что человека, что компьютера, приносит каждой стороне от 50 до 60 очков (сумма длин найденных слов), то есть находятся в основном 5-буквенные слова, ну и очень редко 6-буквенные и выше. А вот компьютер наткнулся на несколько гораздо более интересных вариантов — и суммарный счет порой зашкаливал за 150!
Оцените, балдисты! Часто ли вам приходилось отправлять противника в нокаут шикарным 11-буквенным словом? А у моего компьютера получилось!

