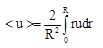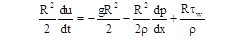Измерение уровня жидкости в топливном баке ракеты22.04.2018 12:18

sodntktscvzakaculh5ctrjyybs.png

Введение

Топливо из резервуара окислителя и резервуара горючего поступает в камеру сгорания ракетного двигателя. Синхронная подача топлива в заданной пропорции обеспечивает эффективную работу ракетного двигателя.

Эффективная работа зависит от точного измерения уровня топлива в баке. Для этой цели топливный бак имеет систему управления топливом. Система представляет собой вертикальный измерительный канал с датчиками внутри канала для фиксации свободного уровня жидкости в канале [1]:

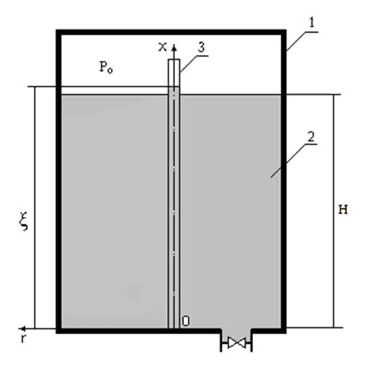
_dqfrmrnkmhp6bnwc-ethxaswtc.png

Рисунок. Схема топливного бака. 1- резервуар, 2- топливо, 3- измерительный канал, Po — давление газа, 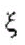3ojrok6yvyqol1uwfs2olgxu7s8.png — уровень жидкости в канале, H — уровень жидкости в баке, r, x — координатные оси.

Вертикальный канал и топливный бак являются сообщающими сосудами. При снижении уровня топлива в баке, уменьшается и уровень топлива в измерительном канале. Когда уровень топлива в канале достигает датчика, происходит активация датчика. Сигнал поступает в систему управления топливом.

В результате расхода топлива его уровень в баке меняется. Таким образом, уровень топлива в канале должен определять уровень топлива в баке. Проблемы две. Первая методическая состоит в том, что свободная поверхность топлива в баке не совпадает с поверхностью топлива в канале.

Вторая проблема в колебаниях уровня при изменении ускорений ракеты в полёте, что приводит к ложным срабатываниям датчиков и, как следствие, к погрешностям измерения.

Ошибка измерения уровня топлива приводит к неэффективному расходу топлива. В результате ракетный двигатель работает не оптимально, а в танках может оставаться «лишнее» количество топлива.

Далее рассмотрим, как можно определить методическую погрешность от первой проблемы и уменьшить погрешность измерения от второй.

Чтобы не отправлять читателя по ссылке [1], приведу здесь вывод дифференциального уравнения движения жидкости в измерительном канале, заодно исправив математические и грамматические ошибки.

Во время полёта t уровень жидкости H в топливном баке изменяется согласно соотношения:

gkfqiyhiqitwv_3uujwhbvkpm8u.png (1)

где: kqqretsl7eep6flmzlssgeaz64w.png–начальный уровень топлива в баке; V– скорость изменения уровня топлива.

При введенной системе координат (смотри рисунок), уравнение для нестационарного движения вязкой несжимаемой жидкости в измерительном канале будет иметь вид:

lx7lqyzducouioqgqdkjarl3pv4.png (2)

При граничных nn98k9_eio1odoti8c_w3d7vc1c.png и начальных g9npeh5sez8-aiayanvkkufq2u8.png условиях.

где: u (r, t) — скорость жидкости в канале; p — давление; ρ — плотность; время — t; v — кинематическая вязкость; g- ускорение силы тяжести.

Получим соотношение для средней скорости в измерительном канале: gs3ykfysiwcyrqrwz9ziwvw_gu8.png

Умножая левую и правую части уравнения (2) на r, запишем отдельные члены уравнения движения:

gymrvx08xyd_79kib1dl0z5amfo.png (3)

где: lmhsyobv2jqiift5yjsx4niikui.png трение; 5vfu5xnz7bdrdoj1nsdnkt4bdpu.png трение стенки; kfxszzmbeu7dnmfcnlqnjxslisu.png динамическая вязкость; R- радиус цилиндрического канала.

Используем уравнения (3) и записываем уравнение (2) в виде (скошенные скобки со средней скоростью в дальнейшем опущены):

mxeoffzknh-ijzre23sxn4tcpyy.png

или

-bxgu7avnus5ly9-9jiykt_m_iw.png (4)

Выберем в цилиндрическом канале объем жидкости двумя поперечными сечениями на расстоянии sxrp-syayimkvscw8xmqb0slqro.png. Запишем для выбранного объёма баланс давления и трения: znqkvahsifqofe0reevxjfc1bwm.png, получаем соотношение:

vxjqk2kn7jjkhv3hz8y-nlxsr2u.png (5)

Используем уравнение Дарси-Вейсбаха -xx_ic1edhtg5fd0xxaeoqfy9iu.png объединив его с (5) получим: 4_ipmticbqfhbyiznubyjaibmg8.png, отсюда соотношение для трения жидкости о стенки измерительного канала примет вид:

jkyiau_vymoqv4dentbechd5jre.png (6)

где λ– коэффициент гидравлического трения.

Подставим (6) в уравнение (4) и получим следующее выражение:

-m8zuhrev9bnpu5wjv1zwb5hxhy.png (7)

Рассчитаем градиент давления при следующих условиях: давление линейно уменьшается от давления наддува над свободной поверхностью топлива до давления 5-7ls3xxzqu67rxe0nx-izhluqy.png. Градиент давления с учётом (1) будет равен:

gbbq4rpxw1hy8mn-padmf4i4lrw.png (8)

Подставив (8) в соотношение (7), получим окончательное дифференциальное уравнение для уровня жидкости в измерительном канале:

cnwkkdwd8o4_gteqc1ydh_c0vpi.png (9)

С начальными условиями Коши, вида:

yjek8_gkmvo0iue0b9n6pljbkwu.png (10)

Решим дифференциальное уравнения (9) с начальными условиями (10)[2].

Рассмотрим условия измерения уровня жидкости в топливных баках ракеты с целью выбора метода обработки измерительной информации, используя решение уравнения (9)

а) Измерение уровня в условиях отсутствия шумов в измерительном канале и колебаний топлива. Зависимость результатов измерения уровня от времени полёта ракеты определяется с использованием следующей программы: 

# -*- coding: utf8 -*-    
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt 
R=0.0195 # радиус измерительного канала в м
H=8.2# начальный уровень в топливном баке, в м
g=9.8# ускорение свободного падения в м/с2
L=4.83*10**-2# коэффициент гидравлического трения
V=0.039# средняя скорость изменения уровня жидкости в м/с
def f(y,t):
         y1,y2=y
         return [y2,-g+(g*(H-V*t)/y1)+((L/(4*R))*y2**2)] 
t = np.arange(0,10,0.01)
y0=[H,0]
[y1,y2]=odeint(f,y0,t,full_output=False).T
plt.title('Измерение уровня топлива при отсутствии помех')  
plt.ylabel('H,m')
plt.xlabel('t,s')  
plt.plot(t,y1,"b",linewidth=2,label='Уровень топлива в измерительном канале ')
y=H-V*t
plt.plot(t,y,"--r",linewidth=2,label='Действительный уровень топлива в баке')
plt.grid(True)
plt.legend(loc='best')
plt.show()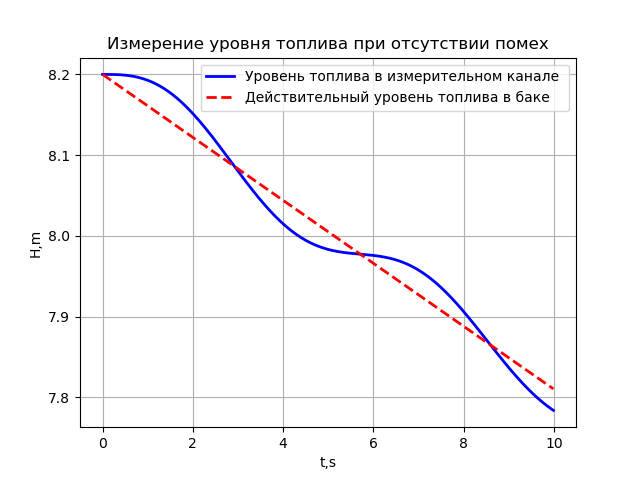

lgyykbnie6cgfjzuhx9dayw675e.png

Это кажущееся решение первой проблемы (за счёт градуировки) при отставании уровня в измерительном канале от уровня в баке. Поскольку в реальных условиях эксплуатации колебания уровня и шумы датчиков вносят существенную погрешность в измерение.

б) Измерение уровня в условиях нормально распределённых случайных колебаний и шумов с дисперсией 0.1. Зависимость результатов измерения уровня от времени полёта ракеты определяется с использованием следующей программы: 

# -*- coding: utf8 -*-    
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt 
R=0.0195 # радиус измерительного канала в м
H=8.2# начальный уровень в топливном баке, в м
g=9.8# ускорение свободного падения в м/с2
L=4.83*10**-2# коэффициент гидравлического трения
V=0.039# средняя скорость изменения  уровня  жидкости в м/с
def f(y,t):
         y1,y2=y
         return [y2,-g+(g*(H-V*t)/y1)+((L/(4*R))*y2**2)] 
t = np.arange(0,10,0.01)
y0=[H,0]
[y1,y2]=odeint(f,y0,t,full_output=False).T
y1= np.array([np.random.normal(x,0.1) for x in y1])#наложение шума на результат измерений
plt.title('Измерение уровня в условиях нормально распределённых случайных \n колебаний и шумов с дисперсией 0.1')  
plt.ylabel('H,m')
plt.xlabel('t,s')  
plt.plot(t,y1,"b",linewidth=2,label='Уровень топлива в измерительном канале ')
y=H-V*t
plt.plot(t,y,"--r",linewidth=2,label='Действительный уровень топлива в баке')
plt.grid(True)
plt.legend(loc='best')
plt.show()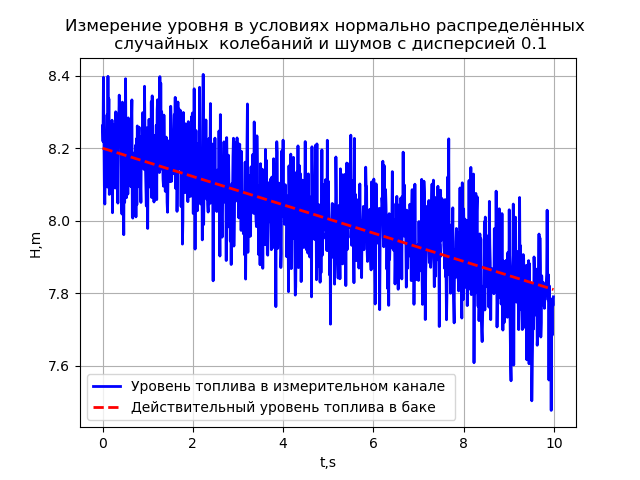

hxspnraylqffluu1hbe5nrkw9_g.png

Приведенный результат подтверждает вывод о том, что измерение уровня в таких условиях с приемлемой погрешностью в несколько процентов от диапазона невозможно.

г) Измерение уровня в условиях нормально распределённых случайных колебаний и шумов с дисперсией 0.1 с использованием фильтра Калмана. Зависимость результатов измерения уровня от времени полёта ракеты определяется с использованием следующей программы: 


# -*- coding: utf8 -*-    
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from numpy import*
from pykalman import KalmanFilter
R=0.0195
H=8.2
g=9.8
L=4.83*10**-2
V=0.039
def f(y,t):
         y1,y2=y
         return [y2,-g+(g*(H-V*t)/y1)+((L/(4*R))*y2**2)] 
t = arange(0,10,0.01)
y0=[H,0]
[y1,y2]=odeint(f,y0,t,full_output=False).T
y=array(H-V*t)#действительный уровень топлива
measurements = array([random.normal(x,0.1) for x in y1])
kf = KalmanFilter(transition_matrices=[1] ,#матрица перехода
                  observation_matrices=[1],#матрица наблюдения
                  initial_state_mean=measurements[0],#среднее начальное состояние
                  initial_state_covariance=1,#ковариация начального состояния
                  observation_covariance=1,#ковариантность наблюдения
                  transition_covariance= 0.001) # ковариантность перехода
state_means, state_covariances = kf.filter(measurements)#среднее  начальное, начальная ковариация
state_std = sqrt(state_covariances[:,0])
plt.figure()
plt.title('Измерение уровня топлива с использованием фильтра Калмана')  
plt.ylabel('H,m')
plt.xlabel('t,s') 
plt.plot(measurements, '-r', label='измерение уровня топлива')
plt.plot(state_means, '-g', label='kalman-выход фильтра')
plt.plot(y, '-k', label='действительный уровень топлива')
plt.legend(loc='best')
plt.figure()
measurement_std = [std(measurements[:i]) for i in  arange(1,len(measurements),1)]
plt.plot(measurement_std, '-r', label='measurment std')
plt.plot(state_std, '-g', label='kalman-filter output std')
plt.legend(loc='upper left')
plt.show()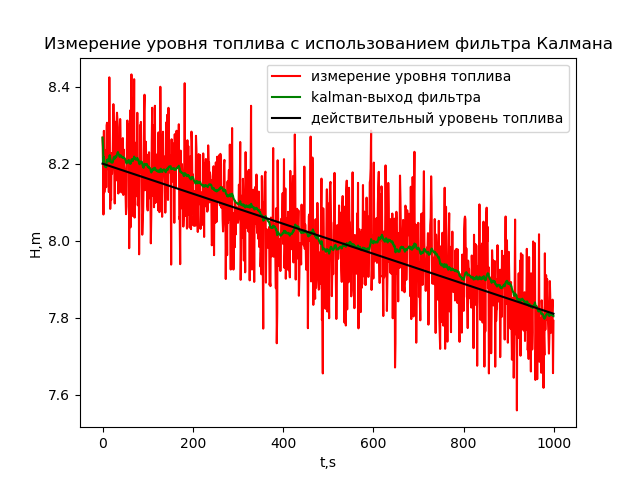

gngfmcgstjuxghzap_zg2uzyd64.png

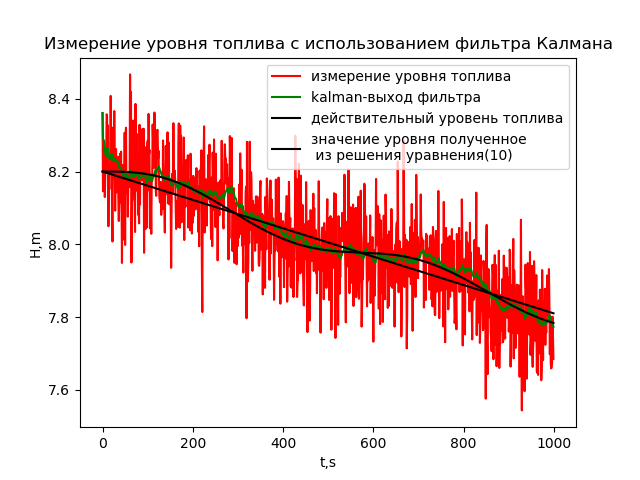
Как видно из графика, фильтр отсеял случайные составляющие и усреднил значения. Однако, фильтр Калмана «ещё умнее» и, при определенной настройке, может даже снизить методическую погрешность:

ngjnw7h6wwv1advsz1wjxqlwuye.png

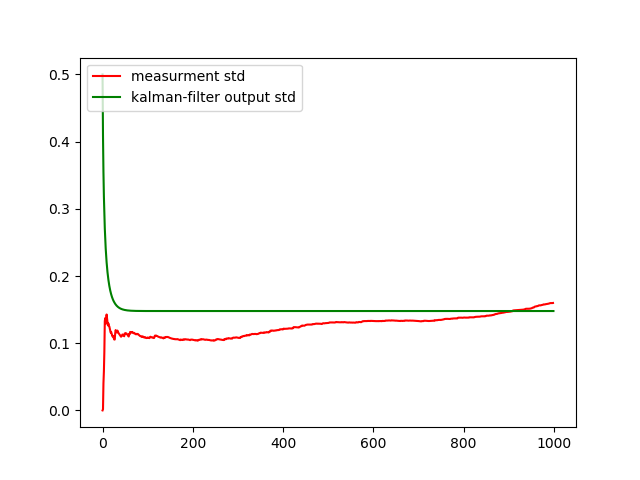
ekwbomwgqinuuc2xwhwwqchkpxa.png

Выводы

Измерение уровня жидкости в топливных баках ракеты в условиях нормально распределённых случайных колебаний уровня и шумов датчиков с дисперсией 0.1 возможно только с использованием фильтра Калмана.

Ссылки

1. Измерение уровня жидкости в топливном баке ракеты.

2. Подвесные топливные баки для самолётов.

© Habrahabr.ru