Избыточность сочетаний29.09.2016 10:18

Сразу отмечу, что данная заметка больше дискуссионная, нежели постулирующая. В Интерне можно найти довольно много описаний и реализаций алгоритмов генерации сочетаний. Тем не менее, вероятно, можно выделить два основных — рекурсивный и тот итерационный алгоритм, который опубликован в книге Липского «Комбинаторика для программистов». Возможно, есть какие-то алгоритмы, существенно отличающиеся от двух указанных. По крайне мере, вполне справедливо предположить, что сочетания можно генерировать с помощью псевдослучайных чисел, но это, вероятно, — самый долгий путь. Несмотря на достаточную краткость и изящность алгоритма из книги Липского, он мне не показался совсем простым, а некоторые другие реализации видятся довольно запутанными. Пример.

Моя идея

Я решил попробовать вывести алгоритм генерации сочетаний в более доступной форме, пусть с некоторым ущербом для времени выполнения или соответствия формуле. Попробую сразу показать на примере свою идею. Есть входной массив А=12345, n=5, допустим, к=3.
Для формирования сочетаний предлагается следующее:
1) Создать матрицу из элементов массива по к элементов, например, двумерный массив вида:

123
234
345

2) Вторым шагом перебирать массив А в цикле с 1 до n и подставлять каждый элемент А на каждую позицию в матрице.
3) Печатать каждую подстановку.

В принципе это все. В результате работы будут сформированы все сочетания, но с дубликатами. Чтобы уменьшить избыточность, можно не подставлять элемент А в те подмассивы, в которых он уже присутствует.

Для сравнения приведу результат работы строгого алгоритма и данного. Для
n=7, k=4 — это 35 уникальных сочетаний, как и должно быть по формуле. Данный алгоритм генерирует 44 сочетания, т.е. среди них 9 дубликатов.

В заключение о плюсах и минусах: главный плюс, пожалуй, — это то, что программа разделена на два блока — генерация матрицы и её обход. Обход матрицы осуществляется в четыре цикла (столько получилось у меня), но без дополнительных условий, что добавляет прозрачности реализации. К минусам можно отнести небольшую избыточность и нелексикографический порядок объектов.

Я не хотел сначала публиковать код, но чтобы заметка не казалась совсем теоретической, прячу под спойлер прототип (можно сказать, первый набросок) данного алгоритма на PHP:

Код алгоритма. PHP
$a = array(
	1,
	2,
	3,
	4,
	5
);
$n = count($a);
$k = 2;

//Формирование двумерного массива по k

$b = array();
$j = 0;

while ($j != $n - $k + 1)
	{
	$i = 0;
	while ($i != $k)
		{
		$b[$j][$i] = $a[$i];
		$i++;
		}

	$j++;
	array_shift($a);
	}

//Обхом матрицы с подстановкой элемента

function change($val, $i, $k)
	{
	$j = 0;
	print_r($val);
	print '
';
	while ($j != $k)
		{
		$c = $val;
		while (true)
			{
			$c[$j] = $i;
			print_r($c);
			print '
';
			unset($c);
			break;
			}

		$j++;
		}
	}

$i = 1;

while ($i != $n)
	{
	foreach($b as $val)
		{
		if (!in_array($i, $val))
			{
			change($val, $i, $k);
			}
		}

	$i++;
	}

Комментарии (5)

  • 29 сентября 2016 в 04:29

    +1

    ↑

    ↓

    В начале стать ни ссылки, ни определения что такое «сочетание» я не нашел, пришлось гуглить (со студенческой парты я все время путал сочетания и размещения, имею я право забыть?).


    Опять же, я вынужден гуглить «алгоритм из книги Липского».


    Кстати, сайт (ваша ссылка с «запутанными» примерами) тоже хорош — 2 простыни кода, без малейшего объяснения, как же он работает.


    «А=12345, n=5, допустим, к=3.» — что такое n и k в вашем случае? Конечно, я догадался, но: на том сайте и я в универе юзали обозначения m и n. У кого-то может возникнуть путаница.


    Почему-то продолжить пример с n=5 и k=3 во 2 м и 3 м пункте вашего алгоритма вы не стали. А я голову ломал.


    «главный плюс, пожалуй, — это то, что программа разделена на два блока» ээ… так, а в чем плюс то?


    Что-то я вообще не понял, зачем вы придумали этот алгоритм, когда он еще и генерирует лишние сочетания, которые нужно потом находить (лишние проблемы и затраты).


    Я лично думаю, что используя формулу 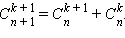image, можно написать достаточно интуитивный рекурсивный алгоритм. Да и формула сама интуитивна (если нарисовать на бумаге).

    • 29 сентября 2016 в 09:45

      0

      ↑

      ↓

      Кстати, сайт (ваша ссылка с «запутанными» примерами) тоже хорош — 2 простыни кода, без малейшего объяснения, как же он работает.

      Тут только могу развести руками. Именно поэтому сел искать что-то более наглядное, о чем и сказал в статье.

  • 29 сентября 2016 в 06:38

    0

    ↑

    ↓

    А почему вы именно таким образом создавали матрицу? У меня вообще возникает вопрос, по поводу втискивания 5 элементов в матрицу из 9ти элеметов.
    Помню, когда-то искал все сочетания, всё это довольно легко визуализируется, если вам надо найти все сочетания для 3 элементов, каждый из которых может быть 5ти разных значений. то это пятиричная система и в ней 3 разряда, дальше просто считаете попорядку в пятерчной системе и выводите результат.
    Например (по проще), 3 элемента у которых 2 значения (A=0,1, n=2, k=3)
    000
    001
    010
    011
    100
    101
    110
    111
    Если надо считать быстро, можно использовать подход, аналогичный двоично-десятичным преобразованиям, а элементы могут быть не только числами, просто берите по индексу.

    • 29 сентября 2016 в 08:07

      0

      ↑

      ↓

      Возможно я ошибаюсь, но в статье приводятся комбинации без повторения одного числа несколько раз в одной строке. Т.е. мы не можем из 12345 создать комбинации: 11112, 11113 и т.д.

      • 29 сентября 2016 в 09:46

        0

        ↑

        ↓

        Все верно. В учебниках часто их называют сочетания.

© Habrahabr.ru