Из жизни маленькой криптосистемы
(на картинке изображен Доктор Тахер Эль-Гамаль, известный криптограф)Как известно, Криптогра́фия (от др.-греч. κρυπτός — скрытый и γράφω — пишу) — наука о методах обеспечения конфиденциальности (невозможности прочтения информации посторонним) и аутентичности (целостности и подлинности авторства, а также невозможности отказа от авторства) информации.Если проще, то (далее я постараюсь излагать все максимально простым языком, легким для понимания):
Криптограффия — это наука, изучающая математические преобразования над информацией, для скрытия смысловой состовляющей этой информации.
В криптограффии есть четыре основопологающих понятия:
Открытый текст (m — от слова message, англ. сообщение) — исходные данные Ключ (k) — параметр криптоалгоритма Криптоалгоритм (f (m, k))– это ОБРАТИМАЯ математическая функция (или набор функций) над открытым текстом, с использованием ключа. Шифротекст (c — от англ. Ciphertext) — результат применения криптоалгоритма с неким ключем над открытым текстом. Для дальнейшего чтения необходимо понимать, что все операции производятся над октетами (далее байтами) в чистом виде (или представленными ascii символами). Так как криптограффия — это прикладная наука, проще всего ее представлять на примерах.
Допустим у нас есть один из самых популярных шифров — гаммирование (более известный в народе как шифр XOR для чисел представленных в двоичном коде, но далее это не XOR, а сложение по модулю 2^8).
Передатчик (для xor, а не для сложение по модулю 2^8, просто (+) заменить на |+|, принцип тот же):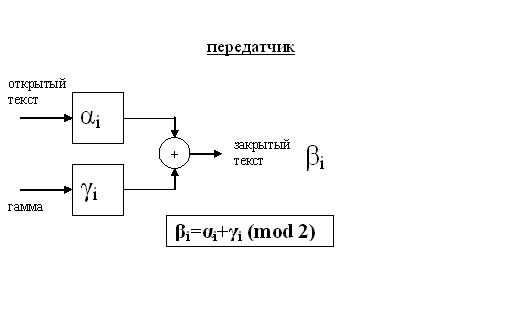 
Приемник: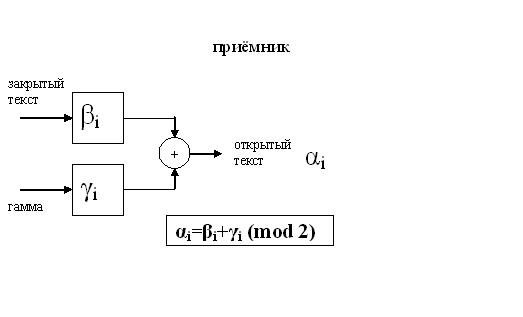 
Допустим, что начальный элемент будет 0, дискретный шаг — 1. Таким образом, в один байт (восемь бит т.к. это октет) можно поместить 256 значений то есть [0; 255]. Кто не вспомнил математику напишу словами — это множество чисел начинающееся 0 до 255 включительно, и как ранее описано с дискретным шагом 1. Т.е. возможные варианты 0, 1, 2, 3, 4… 255.Тогда число комбинаций возможных значений в одном байте — 256, равное количеству элементов, которое можно представить этим байтом. Число комбинаций значений в двух байтах равно 256×256 — т.е. каждому значению первого байта будет отвечать 256 значений второго байта, таким образом получаем 256^2.
Понятно, что для N байт это будет 256^N.
Шифр гаммирования это математическая функция от двух аргументов, как говорилось ранее эти аргументы — это открытый текст и ключ. Пусть размер открытого ключа и текста будет равен одному байту. Тогда:
f (m, k) — это гаммирование в криптографическом представлении f (m, k) = m |+| k — это гаммирование в математическом представлении. Но операция »|+|» и все дальнейшие операции (|-|) будут производится по mod 256, где x mod n это операция нахождения остатка от деления x по модулю n. Результатом x mod n будет число k, k находится в промежутке [0; n), т. е. n — невключительно, что значит, что возможных остатков будет n, а не n + 1.А x можно представить, как x = v*m + k, где v и k — будет одно из допустимых состояний байта ([0; 255] c шагом 1). Если k = 0 (для программистов k == 0) то говорят, о том, что x кратен m.
Теперь допустим, что у нас есть два абонента (Алиса, Боб), которые хотят общатся так, чтобы никто не узнал о чем они говорят. Они используют гаммирование.
Алиса шифрует сообщение:
m = 207; k = 13;
c = 207 + 13 mod 256 = 220; Передает сообщение 220.
Вот тут и начинается праздник. Чтобы расшифровать сообщение Бобу нужна обратная функция шифрования, т.е. функция дешифрования, которая бы сделала m из пары k и с.
~f (c, k) = m
Чтобы функция выглядела как и для шифрования, нужно использовать разные ключи шифрование и расшифрования. Для вычисления ключа расшифрования необходимо решить уравнение:
с |+| d = 0, где d — некая дельта d = ~c |+| 256 = ~c = 36, где ~c — это обратный элемент, и это будет соответствовать бинарному отрицанию для всего байта плюс 1 (220 = 11011100 ~220 = 00100011 = 35 и 35 + 1 = 36) и c |+| ~c = 0, проверим: 220 + 36 mod 256 = 0
k = m |+| d = 207 |+| 36 = 243 Понятно, что однуму и тому же ключу шифрования при разном шифр-тексте будут соответствовать разные ключи расшифрования.
Тогда:
~f (c, k) = 220 |+| 243 = 207 = c |+| ~c |+| m = m (220 + 243 = 463, 463 mod 256 (т.е. 463 — 256) = 207) Теперь допустим, что злоумышленник знает с (а он его по умолчанию знает, т.к. сообщения передаются открыто или грамотнее сказать «по открытому каналу»). Да, он может легко найти d, но ему не найти ключа расшифрования, т.к. он не знает сообщения. Допустим, он может подобрать сообщение, тогда число комбинаций сообщения равно 256 (это оговаривалось выше, из-за размера байта). Тогда зная с и m можно вычислить ключ шифрования и расшифрования, но зачем? (хорошие абоненты используют разные ключи или хотябы ключевой, криптостойкий ГПСП). Время на подбор сообщения — велико, из-за разности смысловой состовляющей, которую оно интерпритированно может давать в контексте. Это как гадать пальцем в воду, да, легко составить 256 комбинаций, но тяжко определить, что это именно правильная комбинация.
Второй вариант, это когда злоумышленник будет подбирать ключ. Для этого ему прийдется подобрать ключ, с числом комбинаций 256, плюс расшифровать шифр-текст.Т.к. время шифрования (и дешифрования) для всех возможных k, c равно и является определенной величиной обозначим его за t. Пользователю для шифрования и расшифрования необходимо 2t + dt, где dt — затраты времени на нахождение ключа расшифрования. То злоумышленнику нужно 256t для вычисления всех возможных комбинаций шифр-текста под ключи.
Отсюда можно очень хорошо увидеть, что, чем длиннее ключ шифрования (как и следствие расшифрования), то тем большее число комбинаций этого ключа существует.ЭТО УВЕЛИЧИВАЕТ НЕОПРЕДЕЛЕННОСТЬ. Чем больше неопределенность пользовательского ключа (чем он длинее и разнообразнее) тем больше времени злоумышленнику нужно будет на подбор ключа.
Допустим, при шифровании из 256 можно выпилить все нерабочие символы и оставить только английские буквы и знаки, тогда это будет приблизительно 80 штук. И все равно это очень большая цифра.
Допустим, используем ключевой ГПСП (генератор псевдо-случайной последовательности), тогда чтобы просчитать гамму на 100 символов текста, нужно просчитать 100 значений ГПСП для каждого ключа + расшифрование.Это выходит 80×100t (гпсп) * t, где t (гпсп) — время работы гпсп. Это при том, что ключ состоит из одного осмысленного символа. А если их N? Тогда:
T (полного перебора) = 80^N * 100t (гпсп) * t Выбирайте неосмысленные пароли побольше, и будет вам счастье. Даже если t расшифрования и работы ГПСП крайне мало (а его можно очень сильно уменьшить, можно даже распараллелить работу шифрования, но из-за того, что ГПСП нераспаралелливаемый, то это бессмысленно). При большом N (> 10), это будет огромная потеря времени, по сравнению с который время жизни человека это лишь миг.
Используйте простые алгоритмы, проверяйте свои результаты. Всматривайтесь в суть вещей, которая Вас защищает. Всем аудит и спасибо за внимание.
P.S. тут небыло полей галуа и прочего, потому что, это всего лишь сложные слова, а я постарался обьяснить все более простыми словами.P.S. S поднимем крипто-образованность населения на новый уровень! P.S. S.S. на Сишке:
unsigned char m = 'h'; unsigned char k = 'k'; unsigned char c = k + m; unsigned char kd = (~c) + 1 + m; unsigned char m2 = kd + c;
